7.3. Задача о финишном рывке

Попробуем несколько обобщить ситуацию, изложенную выше, и рассмотреть антагонистические игры, в которых хотя бы один из противников имеет бесконечное множество чистых стратегий. Такие игры называются бесконечными антагонистическими играми. Их общая теория существенно сложнее теории конечных антагонистических (матричных) игр. Поэтому мы ограничимся рассмотрением только одного примера.

Предварительно введем необходимые для дальнейшего понятия.

Допустим, что каждый игрок имеет бесконечное множество (континуум) чистых стратегий. Причем чистые стратегии игрока I представлены точками единичного отрезка 0≤ξ≤1, а стратегии игрока II - точками единичного отрезка 0≤η≤1. Иными словами, чистые стратегии игроков - это точки (числа), заключенные между нулем и единицей. Роль платежной матрицы (a_ij). играет в этом случае некоторая функция V(ξ, η) Двух аргументов ξ и η. Ее называют функцией выигрыша или ядром игры. Геометрическим образом функции выигрыша является некоторая поверхность, расположенная над единичным квадратом K = {0≤ξ≤1;0≤η≤1}(рис. 22). При выборе первым игроком стратегии ξ₀, а вторым - стратегии η₀ выигрыш первого становится равным V(ξ₀, η₀) - аппликате z₀ точки поверхности с абсциссой ξ₀ и ординатой η₀.

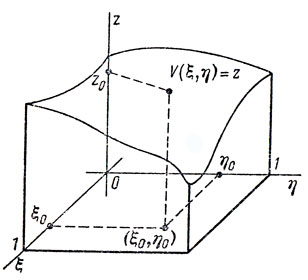
Рис. 22

Рассмотрение игры с функцией выигрыша проводится аналогично конечной игре. Сначала для каждого фиксированного значения ξ из отрезка [0, 1] находят минимум функции V(ξ, η) по всем η: min0≤η≤1 V(ξ, η). Затем отыскивают максимальное из полученных значений по всем ξ:

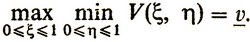
Тем самым получают нижнюю цену игры (максимин) v. Далее находят, подобно предыдущему, верхнюю цену игры (минимакс) :

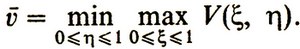
Уже известно, что всегда выполнено неравенство 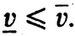. Если верхняя цена игры равна нижней (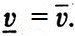), то это означает, что существует такая пара (ξ₀, η₀) чисел, для которых

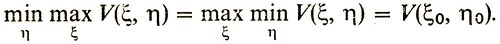
В этом случае игра имеет решение в чистых стратегиях: первый игрок должен постоянно придерживаться своей стратегии ξ = ξ₀, а второй - своей стратегии η = η₀. Стратегии эти оптимальные. Первый игрок выиграет V(ξ₀, η₀), а второй выиграет - V(ξ₀, η₀). Соответствующая точка с координатами (ξ₀, η₀, z₀ = V(ξ₀, η₀) называется седловой точкой. В ней одновременно достигаются минимум по переменной η и максимум по переменной ξ (рис. 23). Ни одному из игроков нет смысла отклоняться от своей оптимальной стратегии : отклонение может привести лишь к уменьшению выигрыша (при условии, что противная сторона продолжает придерживаться своей оптимальной стратегии).

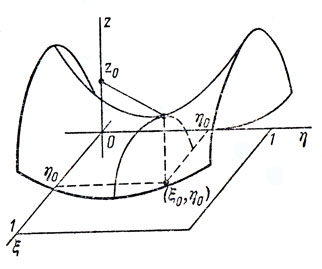
Рис. 23

В том случае, когда верхняя цена игры больше нижней, то решения в чистых стратегиях не существует. Решение следует искать только в смешанных стратегиях. Это означает, что стратегии ξ и η считаются в рассматриваемой ситуации случайными величинами и задаются своими функциями распределения вероятностей P₁(ξ) и P₂ (η). Значение P₁(ξ₁) функции при фиксированном ξ = ξ₁ дает вероятность того, что выбранное случайно на отрезке [0, 1] число ξ окажется меньшим, чем ξ₁. Аналогичный смысл имеет функция P₂(η): ее значение P₂(ξ) при η₁ равно вероятности того, что для выбранного случайно на отрезке [0, 1] числа η выполняется неравенство η<η.

В теории бесконечных игр доказано, что при условии непрерывности функции выигрыша V(ξ, η) всегда существуют оптимальные стратегии (т. е. решение игры).

Займемся теперь конкретной задачей. Два скорохода бегут на коньках стайерскую дистанцию в 10 000 метров. Каждый из них знает, что может решиться не более, чем на один рывок (спурт). При этом естественно считать, что любой из конькобежцев замечает рывок своего соперника.

Введем в рассмотрение функцию P₁ (ξ), определенную на единичном отрезке 0≤ξ≤1. Предположим, что при каждом ξ значение P₁ (ξ) определяет вероятность успеха - выигрыша дистанции конькобежцем - при условии, что он спуртовал на расстоянии, удаленном от места старта не более, чем на ξ. Здесь мы "пронормировали" дистанцию, положив, удобства ради, ее длину, равной единице (значение ξ = 0 отвечает началу, а ξ = 1 - концу дистанции). Таким образом, P₁(ξ) - это функция распределения вероятностей успеха (победы) первого конькобежца на дистанции забега. Естественно предположить, что функция успеха P₁ (ξ) непрерывна для всех значений ξ из [0, 1] и монотонно возрастает от значения P₁(0) = 0 до значения P₁ (1) = 1. Потребуем, чтобы аналогичным условиям удовлетворяла функция P₂ (η), представляющая собой распределение вероятностей успеха второго конькобежца на той же дистанции.

Условимся считать (это тоже своего рода нормирование), что если игрок I обгоняет второго, то его выигрыш (успех) равен +1; если они финишируют одновременно, то выигрыш игрока I равен 0; в случае, когда финиширует первым игрок II, игрок I выигрывает - 1.

Составим теперь функцию выигрыша V(ξ, η) игрока. Если ξ<η, т. е. если игрок I (конькобежец) спуртует раньше игрока II, пройдя расстояние ξ, то вероятность его отрыва и выигрыша составит P₁(ξ). Понятно, что если игрок II не отстанет от игрока I, то в результате уже своего спурта игрок II оторвется и выиграет с вероятностью P₂(η), где η = ξ.

Аналогичные рассуждения можно провести для игрока II. А именно, если он попытается уйти вперед после пройденного расстояния η<ξ, то его успех достигается с вероятностью P₂(η), а его неудача с вероятностью 1-P₂(η).

Итак, выигрыш первого игрока в условных оценках составит

Игры, в которых функция выигрыша игрока II (ядро игры) определяется соотношениями

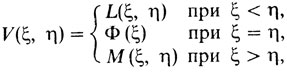
где функции L(ξ, η) и M(ξ, η) определены и непрерывны в квадрате 0≤ξ≤1; 0≤η≤1, а функция Ф(ξ) непрерывна на единичном отрезке 0≤ξ≤1, называются играми с выбором момента времени. Игры такого типа часто встречаются в различных областях человеческой деятельности. Они не всегда обладают оптимальными стратегиями.

В нашем конкретном случае функция выигрыша принимает после очевидных упрощений вид

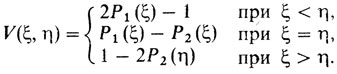
Рассмотрение V(ξ, η) как функции от η при фиксированных значениях ξ наводит на мысль, что игрок I будет иметь оптимальную чистую стратегию, когда постоянная часть выигрыша, т. е. 2P₁(ξ) - 1 (ведь ξ - фиксировано), равна наименьшему значению выражения 1 - 2P₂ (η) для η<ξ. Это требует выполнения равенства

Так как правая часть этого равенства убывает непрерывно от +1 до - 1, когда ξ пробегает отрезок [0, 1], а левая часть возрастает непрерывно от -1 до +1, то существует и может быть найдено хотя бы одно решение ξ₀ этого Уравнения. Отметим, что если обе функции P₁(^) и P₂(η) строго монотонны, то такое решение ξ₀ - единственное.

Допустим в качестве примера, что в нашей задаче P₁(ξ) = ξ, а P₂(η) = η². Тогда функция выигрыша приобретает вид

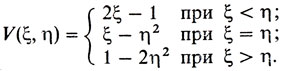
При различных фиксированных значениях ξ можно изобразить линии пересечения поверхности V(ξ, η) плоскостями ξ = const (см. рис. 24).

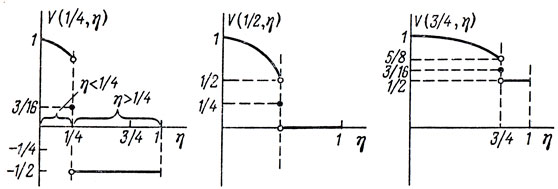
Рис. 24

Так, в частности, при ξ = ¹/₄ (т. е. в сечении плоскостью ξ = ¹/₄) получаем

Решим в нашей конкретной задаче о скороходах уравнение

где P₁(ξ) = ξ, а P₂(ξ) = ξ². Получаем

или

откуда находим 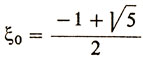(другой корень квадратного уравнения не подходит, так как не принадлежит отрезку [0, 1]).

Таким образом, игрок I должен делать рывок, пройдя

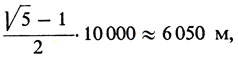
и его ожидаемый выигрыш будет равен 2P(ξ₀) - 1 = √5 - 2 = 0,21.

Итак, при выбранных нами функциях распределения вероятностей P₁(ξ) и P₂(η) у первого конькобежца несколько больше шансов выиграть дистанцию, чем у второго.

В общем случае эту задачу можно решить при тех или иных функциях распределения вероятностей успеха P₁(ξ) и P₂(η) которые могут быть получены эмпирическим путем или методом экспертного опроса тренеров и самих конькобежцев.