
7.2. Немного о матричных играх
Рассмотренная выше математическая модель спортивной ситуации служит примером так называемой конечной игры двух лиц с нулевой суммой. Игры двух лиц занимают центральное место во всей теории игр, и их рассмотрение позволяет понять и изучить основы общей теории и некоторые ее основные результаты.
Конкретизируем понятие конечной игры двух лиц с нулевой суммой. В игре сталкиваются интересы двух игроков I и II. Игра представляет собой свод правил, описывающих сущность конфликтной ситуации. Под правилами игры понимают совокупность условий, предопределяющих возможные действия каждой из сторон на каждом этапе игры, информацию о поведении противной стороны, плату (выигрыш) игрока после завершения любого этапа игры. Реализация игры состоит из последовательных "ходов", т. е. из выбора тех или иных действий из числа предусмотренных правилами. Если выбор образа действий принадлежит самому игроку, ход называют личным. В шахматной игре, например, реализуются только личные ходы. Ход называют случайным, если он выбирается некоторым устройством совершенно случайно (например, бросанием игрального кубика). Стратегией игрока называют совокупность рекомендаций, однозначно предопределяющих выбор действий при каждом личном ходе игрока и в любой ситуации, которая может возникнуть на любом этапе игры. Такие стратегии называют чистыми.
Пусть теперь игрок I имеет m чистых стратегий (ходов) α1, .., αm, а игрок II - располагает n чистыми стратегиями β1, ..., βn. Условимся считать, что если первый игрок выбирает i-ю стратегию αi, а второй j-ю стратегию βj, то первый игрок выигрывает αij условных единиц*, а второй выигрывает соответственно bij = -aij. В силу того, что aij + bij = 0 Для любых i и j, такие игры и называются играми двух лиц с нулевой суммой, или антагонистическими играми. В дальнейшем мы почти всегда будем говорить о выигрыше, ибо проигрыш -это отрицательный выигрыш.
* (Выигрыш (проигрыш) не всегда имеет точное количественное значение. В то же время почти всегда удается его как-то оценить, используя некоторую шкалу измерений. Так, например, выигрышу в шахматной игре можно приписать оценку 1, проигрышу - 1, ничьей 0.)
Таким образом, множество различных исходов, т. е. выигрышей, в этой игре можно задать так называемой платежной матрицей (матрицей выигрышей)
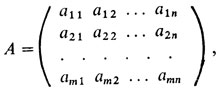
которая указывает на выигрыш игрока I. Иными словами, элемент aij матрицы A означает выигрыш первого игрока при использовании им стратегии αi и при использовании вторым игроком стратегии βi. Поэтому при таком задании игры цель игрока I - максимизировать свой выигрыш, а игрока II - минимизировать его (вновь напомним, что матрица A определяет выигрыш первого игрока и проигрыш второго).
Рассмотрим следующую игру:

Рассмотрим эту игру с точки зрения игрока I. Если бы он знал, каким будет Выбор игрока II, то он бы легко определил свой наилучший ответ, используя следующую таблицу:
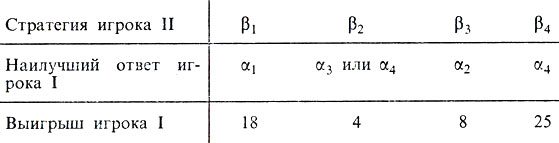
Но поскольку ответный выбор первого игрока зависит от выбора второго игрока, а этот выбор, естественно, неизвестен, то неясно, что же делать первому игроку. Следовательно, первому игроку надо попытаться исследовать, к выбору какой конкретной стратегии приведет анализ ситуации его противником. Поэтому игрок I составляет аналогичную таблицу для выбора наилучшей стратегии игрока II:

Из второй таблицы видно, что если игрок 1 выбирает α1б то ему обеспечен 0, так же как и при выборе α2 и α5; при выборе α3 ему обеспечено 4, а при выборе α4 обеспечено 2. Назовем наименьшую сумму, которую он получает при выборе стратегии, гарантированным уровнем этого выбора. Наибольший из таких уровней называется максимальным гарантированным уровнем, или наилучшим гарантированным результатом. В данном примере, выбирая α3, первый игрок может гарантировать себе выигрыш, по меньшей мере равный 4, и никакая другая стратегия не может гарантировать выигрыш, равный 4.
Встав на точку зрения игрока II, мы заключаем из первой таблицы, что стратегии β1, β2, β3 и β4 обеспечивают соответственно следующие гарантированные уровни: +18, +4, +8 и +25. Таким образом, стратегия β2 гарантирует максимальный уровень 4 (еще раз отметим, что чем меньше число, тем выгоднее игроку II, ибо его гарантированные выигрыши равны соответственно в этой ситуации -18, -4, -8 и -25).
Итак, есть полное основание ожидать, что игрок I будет применять стратегию α3, а игрок II - стратегию β2. Мы можем сказать, что набор стратегий α3 и β2 оптимален в том смысле, что ни одному из игроков не следует менять свой выбор, если другой также не изменит свой выбор.
В общем случае пару чистых стратегий αi0 и βi0 называют оптимальной, если выполняется условие
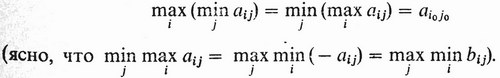
К сожалению, далеко не всегда существует такая пара чистых стратегий; примером этому может служить описанная ранее ситуация с участием тренеров футбольных команд.
Вернемся теперь к общему случаю, когда игра задается некоторой платежной матрицей A = (aij). Если игрок I выбирает в некоторой партии стратегию α1, то наверняка его выигрыш не окажется меньшим минимального элемента из первой строки этой матрицы, т. е. по меньшей мере он выиграет
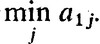
При выборе стратегии αi он получит по меньшей мере
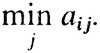
Однако игрок I волен выбирать любую из своих стратегий. Он может поэтому выбрать αi таким образом, чтобы гарантировать себе наименьший из возможных выигрышей, т. е.
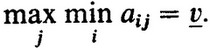
Эту величину называют нижней ценой игры или максиминным выигрышем (максимином). Соответствующую стратегию (она определяется строчкой, где лежит элемент v-) называют максиминной.
Подобно этому, платежи игроку II есть элементы той же матрицы A, ятые со знаком минус. Следовательно, коль скоро этот игрок использует стратегию βj, он получает не менее, чем
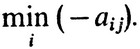
Естественно, что он стремится максимизировать этот выигрыш, используя разные βj, т. е. приходят к
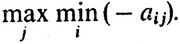
Легко видеть, что для любой функции f(x)
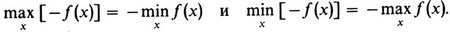
В приложении к рассматриваемой нами ситуации последнее означает, что
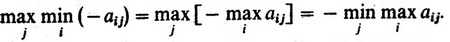
Значит, игрок II может выбрать свою стратегию так, чтобы заведомо получить не менее, чем
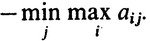
При этом, конечно, игрок I получит самое большое
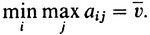
Следовательно, хотя игрок I и может гарантировать себе выигрыш не меньший, чем
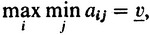
однако игрок II не допустит, чтобы выигрыш игрока I стал большим, чем
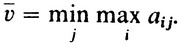
Число v называют верхней ценой игры или минимаксом, а соответствующую стратегию (она определяется столбцом, где лежит число v) - минимаксной.
Может оказаться (как в разобранном выше конкретном примере), что
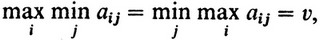
т. е. нижняя цена игры v- равна верхней v-. Это общее значение называют просто ценой игры, и равно оно некоторому элементу ai0j0 матрицы A. В этом случае игрок I понимает, что может выиграть по крайней мере v, а игрок II будет мешать ему получить больше чем v. Поэтому игрок I будет придерживаться стратегии ai0. В то же время игрок II может выиграть не менее, чем - v, коль скоро станет придерживаться стратегии βi0. Элемент ai0j0 = v платежной матрицы (в нашем примере a32 = 4) является одновременно минимальным в строке i0 и максимальным - в столбце j0. Такой элемент называют седловой точкой матрицы А, игру называют игрой с седловой точкой, стратегии αi0 и βj0 - оптимальными для игроков I и II соответственно, а пару (αi0, βj0) - решением игры. Мы приходим к следующему выводу.
Решение игры с седловой точкой является устойчивым, т. е. для любого игрока отклонение от его оптимальной стратегии не приводит к выгоде, если только противник по-прежнему станет придерживаться своей оптимальной стратегии.
Таким образом, оптимальная стратегия при многократном повторении игры с седловой точкой гарантирует игроку максимально возможный средний выигрыш. При этом предполагается, что противная сторона действует столь же разумно и осмотрительно, как и данный игрок.
Что больше - «максимин» или «минимакс»?
Футбольный мотив, с которого мы начали изучение игровых ситуаций, был связан с матрицей
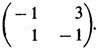
Она не имеет седловой точки. Действительно,
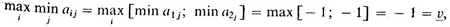
тогда как
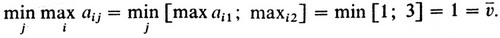
Следовательно, 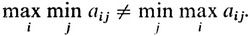
Пусть функция f(x; y) двух переменных определена для каждой пары целочисленных значений x = 1, 2, ... и y = 1, 2, ... так, что f(i, j) = aij. Докажем, что для любой матрицы A = (aij) справедливо неравенство
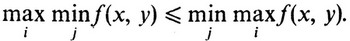
По определению минимума для любых фиксированных x и y
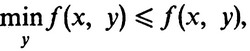
а по определению максимума
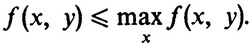
Следовательно,
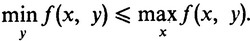
Но левая часть у этого неравенства не зависит от y, поэтому
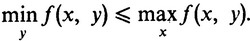
Однако правая часть последнего неравенства не зависит от x. Поэтому
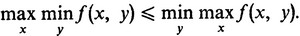
Для завершения доказательства остается только вспомнить, что f(x, y) = f(i, j) = aij (i = 1, ..., n; j = 1, ..., n).
В качестве следствия из доказанного получаем, что в игре, определенной любой матрицей А, нижняя цена игры 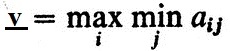 не превышает верхней цены
не превышает верхней цены 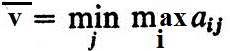 , т. е.
, т. е. 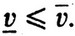 Цена v игры лежит между v- и v-.
Цена v игры лежит между v- и v-.
Можно также показать (мы этого не делаем), что необходимым и достаточным условием выполнения равенства
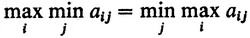
является наличие в матрице A седловой точки. Так, например, матрица
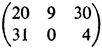
имеет седловую точку a12 = 9 - элемент, наименьший в первой строке и наибольший во втором столбце.
Две седловые точки a11 = 7 и a13 = 7 имеет матрица

При игре с такой платежной матрицей игрок I должен придерживаться стратегии α1, тогда как игрок II может выбрать любую из стратегий β1, β3.
Если игра не имеет седловой точки, то ни один из игроков не обладает единственной наиболее надежной чистой стратегией. В то же время игрок не имеет возможности определить стратегию противника, если последний, вместо того чтобы придерживаться единственной чистой стратегии, начнет использовать набор нескольких чистых стратегий, чередующихся по случайному закону с определенным соотношением частот. Такой набор называют смешанной стратегией. Таким образом, смешанной стратегией называют вектор x = (x1, x2, ..., xn), компонента xi (i = 1, 2, ..., n) которого является вероятностью выбора игроком i-й стратегии αi из совокупности α1, α2, ..., αn его чистых стратегий.
В игре между тренерами Всезнаевым и Находчивым седловой точки не оказалось. Вот почему и тот и другой решили использовать смешанные стратегии.
Остановимся несколько подробнее на понятии смешанной стратегии. Пусть x1, x2, ..., xm - вероятности, с которыми первый игрок может выбрать стратегии α1, α2, ..., αm, а y1, y2, ..., ym - соответствующие вероятности выбора стратегий β1, β2, ..., βn вторым игроком. Очевидно, что
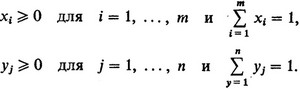
В этом случае средний выигрыш первого игрока (он же проигрыш второго) определяется формулой (она определяет математическое ожидание выигрыша):
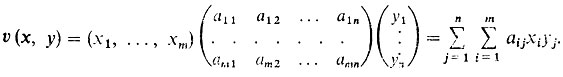
Отметим, что здесь записано произведение матриц: матрица-строка x = (x1, ..., xm) умножается на матрицу A, а затем полученный результат вновь умножается на матрицу-столбец y из элементов y1, ..., yn.
Создателю современной теории игр Дж. фон Нейману (1903-1957) принадлежит доказательство основного факта теории - теоремы о минимаксе (ее доказательство можно найти, например, в [17]).
Теорема фон Неймана о минимаксе утверждает, что существует по крайней мере одна пара векторов x0 и y0, удовлетворяющая приведенным выше ограничениям и такая, что
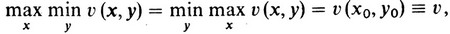
где v - цена игры.
В некоторых играх (шахматы, шашки, крестики-нолики и др.) каждый игрок, реализуя свой очередной ход, знает результаты всех предшествующих ходов обеих сторон. Из общей теории игр известно, что всякая игра такого типа, называемая игрой с полной информацией, имеет седловую точку и потому имеет решение в чистых стратегиях. При этом в среднем игра завершается выигрышем, равным цене игры v.
Чаще, однако, встречаются игровые ситуации с матрицами без седловых точек. В таких играх для достижения наибольшего среднего выигрыша игроки должны придерживаться своих максиминной и минимаксной стратегий. При этом игрок I гарантирует себе выигрыш, равный нижней цене игры v-. Если же этот игрок воспользуется подходящей смешанной стратегией, то сможет повысить свой выигрыш до цены игры v-. Практически при использовании смешанной стратегии перед каждой партией реализуют некоторую систему случайного поиска (например, датчик случайных чисел от 0 до 1 или игральный кубик), способную указать появление каждой из чистых стратегий с соответствующей ей (как компоненте смешанной стратегии) вероятностью. В очередной партии используют именно ту чистую стратегию, на которую выпал жребий.
В смешанных стратегиях для каждой игры с конечной матрицей А размерности m×n существует (и может быть найдена!) пара (x0, y0) оптимальных стратегий игры. Именно это утверждает основная теорема о минимаксе. Оптимальные стратегии обладают устойчивостью в том смысле, что если один из игроков придерживается своей оптимальной стратегии, то другому не выгодно отступать от своей оптимальной стратегии.
Предположим, что для игры мы нашли решение - пару оптимальных стратегий x0 = (x10, ..., x0m); y0 = (y10, ..., yn0). Те из чистых стратегий αi (соответственно βj), которым отвечают нулевые значения вероятностей xi0 = 0 (yj0 = 0), называют пассивными; остальные - активными стратегиями.
Убедимся, что коль скоро один из игроков придерживается своей оптимальной стратегии x0, то его выигрыш не меняется, совпадает с ценой игры и и не зависит от того, какие действия предпринимает второй игрок, если только тот использует лишь свои активные чистые стратегии.
Действительно, пусть, для определенности, активными чистыми стратегиями являются α1, ..., αs (для игрока I) и β1, ..., βr. (для игрока II); остальные - пассивными. Следовательно,
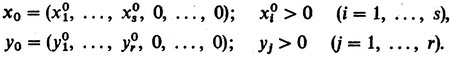
Кроме того, x10 + ... + xs0 = 1; y10 + ... + yr0 = 1. Предположим, что игрок I пользуется своей оптимальной стратегией x0, а игрок II - любыми смешанными стратегиями, составленными только из активных чистых стратегий β1, ..., βr. Если игрок I использует свою оптимальную стратегию x0, а игрок II - свою активную чистую стратегию βj, то игрок I может получить выигрыш vj, который, как следует из основной теоремы, может даже превзойти цену игры: vj ≥ v. Однако в действительности возможно лишь точное равенство: vj = v. В самом деле, ведь в смешанной стратегии y0 чистые стратегии β1, ..., βr используются с вероятностями y10, ..., yr0 соответственно. Поэтому математическое ожидание выигрыша (т. е. средний выигрыш) составит
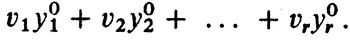
В то же время этот выигрыш должен равняться цене игры
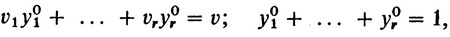
откуда и следует, что ни одна из величин vj не может превосходить цену игры v. Иначе вся сумма превзойдет v.
Скептически настроенный читатель может спросить, имеет ли введение смешанной стратегии какое-либо принципиальное значение? Что значит выбрать смешанную стратегию, и будет ли кто-либо выбирать ее в действительности? Что касается роли смешанной стратегии, то она зависит в значительной мере от субъективного восприятия понятия вероятности. Что же касается выбора "чистой" стратегии при посредстве смешанной, то этот путь эквивалентен проведению некоторого вероятностного опыта. В случае с тренером "Вымпела" Находчивым ему следует, прежде чем осуществить замену, провести опыт с вероятностями исхода 1/3 и 2/3, например, бросить игральную кость. Если выпадет число, делящееся на три, т. е. 6 или 3, то ему надо выпускать нападающего, а в остальных случаях - защитника. Конечно, такая рекомендация может показаться наивной, но в действительности для рассматриваемой ситуации этот прием дает оптимальное поведение. К сожалению, стратегов часто оценивают по исходу принятого выбора, а не по его стратегической целесообразности в общей рискованной ситуации.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'