7. Игровые модели

7.1. "Метеор" - "Вымпел" (на футбольную тему)

Приближался к концу финальный матч за переход в более высокую лигу между командами "Метеор" и "Вымпел". Счет был ничейным, каждая команда имела в запасе по нападающему и защитнику, но могла провести только по одной замене. Тренер "Метеора" Всезнаев знал, что его нападающий переиграет запасного защитника "Вымпела", но проиграет запасному нападающему, в то время как запасной защитник "Метеора" удержит нападающего "Вымпела", но сыграет хуже защитника команды противника. Всезнаев составил следующую таблицу:

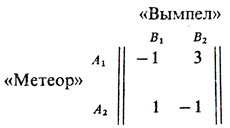
в которой положительное число соответствует преимуществу "Метеора", а отрицательное - преимуществу "Вымпела" (в некоторых условных оценках). Тренер "Метеора" стал рассуждать следующим образом: "Если я выпущу нападающего (назовем это решение стратегией^* A₁) и тренер "Вымпела" это узнает, то он тоже выпустит нападающего (стратегия B₁), и мы проиграем с оценкой - 1 (т. е. преимущество получит "Вымпел"), а если я выпущу защитника (стратегия A₂), то он выставит тоже защитника (стратегия B₂), и мы вновь проиграем с оценкой - 1. Но тренер "Вымпела" Находчивый не знает, что я собираюсь делать. Поэтому он будет считать, что против его нападающего я выпущу защитника, и он тем самым проиграет единицу, а против его защитника я выпущу своего нападающего, и мы получим преимущество в три единицы".

^* (О понятии стратегии подробнее см. дальше.)

Всезнаев был немного знаком с теорией игр и решил выпустить защитника. Почему же он пришел к такому решению?

А потому, что рассуждал следующим образом: "Допустим, что p - вероятность (частота), с которой я выпускаю в ситуациях, аналогичных данной, нападающего. Тогда с вероятностью 1-p я в этих же ситуациях выпускаю защитника. В таком случае, если "Вымпел" выставит нападающего, мы, в среднем, приобретем преимущество, равное

а если Находчивый выставит защитника, то мы, в среднем, приобретем преимущество, равное

Таким образом, Всезнаеву надо найти такое значение p из отрезка [0, 1], при котором наименьшее значение из двух величин v₁(p) и v₂(p) оказывается наибольшим, т. е., как говорят, найти такое p, которое максимизирует минимум из двух величин: v₁(p) и v₂(p). Очевидно, что при увеличении p увеличивается v₂(p), но зато уменьшается v₁(p), и наоборот, уменьшение p повлечет за собой увеличение v₁(p), но уменьшение v₂(p). Всезнаев решил изобразить эти ситуации графически (рис. 20).

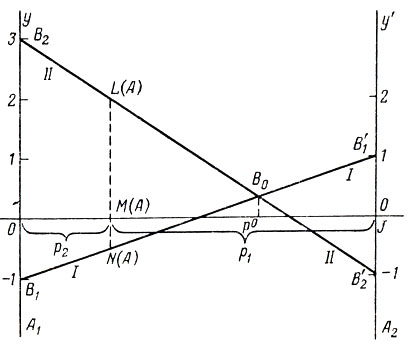
Рис. 20

В качестве оси x он выбрал горизонтальную ось и предназначил ее для изображения величины p. От точки О он отложил единичный отрезок [0, J]. Левый конец (точку О) он отождествил со стратегией A₁, правый (точку J) - с A₂. Всезнаев твердо знал, что придерживаться во всех случаях только одной из этих стратегий, так сказать, в чистом виде (чистой стратегии), нецелесообразно. В самом деле, если использовать A₁ с вероятностью p(A₁) = 0 (т. е. вовсе не использовать), и A₂ с вероятностью p(A₂) = 1, то тренер Находчивый всегда станет выпускать своего защитника. Вот почему Всезнаев обратился к так называемым смешанным стратегиям А, в которых используются чистые стратегии A₁, A₂ с вероятностями p(A₁) = p = p₁ и p(A₂) = p₂ = 1-p. Каждой смешанной стратегии (p₁, p₂) Всезнаев сопоставил точку M_A отрезка [0, J], определив ее так, чтобы расстояние |0 М(А)| = p₁, |M(A) J| = p₂. Затем через концы отрезка [0, J] провел пару вертикальных осей O_y и J_y', перпендикулярных оси Ox. Первую из этих осей предназначил для изображения выигрышей при использовании чистой стратегии A₁, вторую - для выигрышей при A₂. Если Находчивый будет придерживаться своей чистой стратегии B₁, то выигрыш "Метеора" составит - 1 (точка B₁), если он выберет стратегию B₂, то выигрыш станет равным 3 (точка B₂). Это при условии, что Всезнаев остановился на стратегии A₁. Если же он выбрал стратегию A₂, то выиграет либо 1 (при стратегии B₁), либо - 1 (при стратегии B₂). Эти выигрыши Всезнаев изобразил на оси J_y' точками B₁' и B'₂ соответственно. Затем он прямой B₁B'₁ (I) соединил соответствующие точки B₁ и B'₁. Прямая (I) проходит через точки B₁ с координатами (0, 1) и В'₂ с координатами (1, -1). Поэтому ее уравнением в системе координат O_xy служит y = 2x - 1. При любой смешанной стратегии A = (p₁, p₂), примененной Всезнаевым, он получает выигрыш, отвечающий Точке N(A) на прямой B₁B'₁ (стратегия B₁ Находчивого), лежащей над точкой M(A). Действительно, ордината y(А) точки N (А) на прямой (I) равна y(А) = 2p₂ - 1 = 2(1 - p₁) - 1 = 1 - 2p₁ = v₁(p).

Подобным же способом он построил прямую B₂B'₂ (II) (стратегия B₂ Находчивого) и отметил на ней точку L(A), ордината которой - выигрыш при использовании им смешанной стратегии A и при стратегии B₂ Находчивого. На возникшем чертеже величина v₂(p) изображается точкой L(A). Действительно, прямая (II) проходит через точки B₂ (0, 3) и B₂ (0, -1) и определена уравнением y = -4x + 3. При x = p₂ ордината точки L(A) равна y(A) = -4p₂ + 3 = -4 (1 - p₁) + 3 = 4p₁ - 1 = v₂(p).

Всезнаев искал оптимальную для себя стратегию A₀ = (p₁⁰, p₂⁰), т. е. такую, при которой его минимальный выигрыш (при наихудших для него действиях Находчивого) был возможно большим. Он сразу заметил, что ломаная B₁B'₀B'₂ соответствует значениям минимума из двух величин v₁ (p) и v₂ (p) для различных p из отрезка [0, 1] и что максимум этих минимумов достигается в точке B₀, т. е. в точке пересечения прямых (I) и (II).

Всезнаев нашел эту точку пересечения и соответствующее значение p⁰, решив уравнение

или

Решением этого уравнения оказалось значение p⁰ = ¹/₃. Таким образом, в среднем, из трех случаев только в одном надо выпускать нападающего и в двух - защитника. Именно поэтому тренер "Метеора" решил выпустить защитника. Заметим, что такое "максиминное" (новый термин!) значение из значений v₁ (p) и v₂ (p) называется средним выигрышем тренера "Метеора" (отрицательный выигрыш - это проигрыш, но в теории игр всегда говорят о выигрыше). В нашем случае этот выигрыш составит при p⁰ = ¹/₃

А как же действовал Находчивый - тренер "Вымпела"? Он рассуждал аналогично (не забывайте, его выигрыш - отрицательные числа!): "Пусть с вероятностью q = q₁ я выпущу нападающего, а с вероятностью 1 - q = q₂ - защитника. Если Всезнаев выпустит нападающего, то наш выигрыш составит

а если тренер "Метеора" выпустит на поле защитника, то наше преимущество оценится величиной

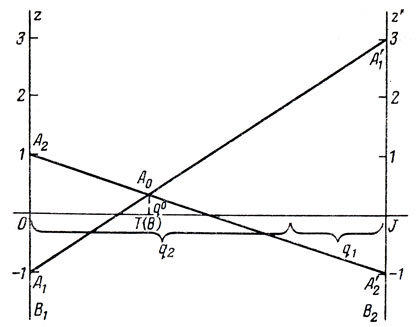
Рис. 21

Затем Находчивый также построил чертеж (рис. 21), аналогичный чертежу Всезнаева. Каждой точке T(В) единичного отрезка [0, J] он сопоставил свою смешанную стратегию B = (q₁, q₂) так, чтобы |OT(B)| = q₂, |T(B)J| = q₁. Оси Oz и Oz' он предназначил для изображения выигрышей при использовании чистых стратегий B₁ и B₂ соответственно. Если при выборе стратегии B₁ Всезнаев выпустит нападающего (стратегия A₁), то выигрыш Находчивого составит - 1 (точка A₁). Если же Всезнаев выпустит защитника, то выигрыш Находчивого составит (точка A₂). При использовании только стратегии B₂ на оси Oz' возникают точки A₁' (выигрыш, равный 3) и A₂' (выигрыш -1). Находчивый подсчитал, что в системе координат xOz ординаты прямых A₁A₁' и A₂A'₂ определяют соответственно v₁(q) и v₂(q). Цель Находчивого состоит в нахождении такого q из [0, 1], которое минимизировало бы максимум двух величин v₁(q) и v₂(q), так как, чем меньше эта величина, тем выгоднее команде "Вымпел". Положительные числа - это выигрыш "Метеора", а отрицательные - "Вымпела". Посмотрев на рисунок, тренер "Вымпела" заметил, что ломаная A₂A₀A₁' соответствует максимальным значениям из пары чисел v₁(q) и v₂(q) для различных q из отрезка [0, 1], а точка A₀ - минимуму из этих максимумов, следовательно, при соответствующем значении q⁰ достигаются так называемые "минимаксные" (также новый термин!) значения v₁(q) и v₂(q). Решая уравнение

или

он нашел, что q⁰ = ²/₃, т. е., в среднем, в двух случаях из трех целесообразно выпускать нападающего и только в одном случае - защитника. Средний выигрыш команды "Вымпел" в этом случае составит

Следовательно, команда проиграла ¹/₃, так как ее выигрыш - отрицательное число, а проигрыш - положительное. Нетрудно понять, что сколько в среднем выиграл "Метеор", ровно столько же проиграл "Вымпел", и наоборот, т. е. сумма выигрышей двух этих команд равна нулю. Такие игры, в которых суммарный выигрыш равен 0, называются играми с нулевой суммой.

На примере действий тренера Всезнаева читатель познакомился с методикой принятия решения на основе рекомендаций математической теории игр. Знакомство окажется приятней и полезней, если его подкрепить дополнительными сведениями. К их изложению мы переходим.