6.10. Некоторые общие суждения

В каждой из разобранных выше задач поиск оптимального решения начинался с некоторого исходного допустимого базисного решения X₀ системы ограничений задачи. Затем осуществлялся переход к другому допустимому базисному решению X₁ доставлявшему минимизируемой форме меньшее значение, чем решение X₀. От решения X₁ делался переход к решению X₂ и т. д. до получения желаемого результата. В этом приеме и состоит сущность симплекс-метода.

Вспомним, что каждое допустимое базисное решение определяет некоторую угловую точку выпуклого многогранника решений задачи. Поэтому можно сказать, что, отправляясь от некоторой исходной угловой точки, с помощью симплекс-метода мы выходим на другую угловую точку с меньшим значением минимизируемой формы F(X) и т. д. Уже известно, что если оптимальное значение F(X) на многограннике решений существует, то оно заведомо достигается по крайней мере в одной из его угловых точек (т. е. при некотором допустимом базисном решении).

Реализацию симплекс-метода легко унифицируют и все вычисления проводят с помощью специального вида таблиц {симплекс-таблиц), работа с которыми не представляет труда. В каждую из таких таблиц заносят значения коэффициентов, с которыми базисные неизвестные и форма выражаются через свободные (т. е. определенное допустимое базисное решение). Тем самым таблица представляет собой более экономную запись системы ограничений и минимизируемой формы задачи. По четко установленным правилам работы (именно эти правила были использованы в рассмотренных примерах) от занесенного в таблице решения переходят к таблице с другим Решением и т. д. Описание работы с таблицами читатель может найти почти в каждом руководстве по линейному программированию (например [6; 1]), и мы на этом внимание читателя не фиксируем.

К этому следует добавить, что математическое обеспечение современных ЭВМ располагает специальной программой для решения задач линейного программирования. Поэтому даже нет необходимости учиться решать такие задачи "вручную".

Читатель, по-видимому, заметил, что в разобранных нами задачах линейного программирования значения всех базисных неизвестных в каждом из допустимых базисных решений были отличными от нуля. Это свойство называют невырожденностью;" а именно, задача линейного программирования называется невырожденной, если в каждом из ее допустимых базисных решений значения всех базисных неизвестных строго больше нуля.

В курсах линейного программирования доказывается следующая теорема о симплекс-методе. Предположим, что:

1. задача линейного программирования невырожденная;
2. она имеет по крайней мере одно допустимое базисное решение;
3. минимизируемая форма задачи ограничена снизу на множестве допустимых решений. (Это означает, что любое значение формы на множестве допустимых значений не меньше некоторого фиксированного числа.)

Тогда существует по крайней мере одно оптимальное базисное решение. Это решение может быть достигнуто симплекс-методом исходя из любого начального допустимого базисного решения.

Отметим, что при нарушении условия о невырожденности возможна ситуация, при которой оптимальное решение не достигается, так как не появляется никаких препятствий для перехода от одного допустимого базисного решения к другому. Возникает так называемое зацикливание - явление возможное, но крайне редкое. В геометрическом плане зацикливание означает, что процесс решения "застрял" на некоторой вершине многогранника Q решений. Этой вершине соответствует несколько различных допустимых базисных решений. Симплекс-метод при этом переводит от одного подобного решения к другому без сдвига на другую вершину многогранника Q и без изменения значения формы F(X).

Чтобы начать работу по симплекс-методу, нужно иметь, как мы видели, исходное допустимое базисное решение X₀. В простых случаях X₀ можно подобрать непосредственно (что мы и делали), изучая систему ограничений задачи. Однако при большом числе уравнений и неизвестных необходим иной путь определения X₀. Замечательную возможность для этого открывает тот же симплекс-метод. Более того, одновременно этот метод дает возможность установить, совместна ли система ограничений в области неотрицательных значений неизвестных, т. е. не является ли пустым многогранник Q допустимых решений.

Вот идея этого приема. Перепишем систему (30) ограничений задачи линейного программирования в виде

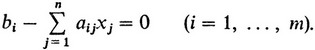(54)

Без нарушения общности можно предположить, что все b_i ≥ 0 (если b_i<0, то умножаем i-е уравнение на - 1). Введем (по числу уравнений) вспомогательные переменные ξ₁, ξ₂, ..., ξ_m, связав их с переменными x₁, x₂, ..., x_n соотношениями

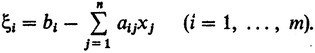(55)

Рассмотрим вспомогательную линейную форму относительно ξ₁:

Начнем минимизировать форму φ(ξ) при ограничениях (54) и условиях неотрицательности неизвестных: ξ₁≥0, ξ₂≥ 0, ..., ξ_m ≥0. Для решения этой, по существу, вспомогательной задачи мы можем сразу же применить симплекс-метод. Действительно, будем считать переменные x_j (j = 1, ..., n) свободными, а ξ_i (i = 1, ..., m) - базисными. При этом возникнет исходное допустимое базисное решение

В силу неотрицательности ξ_i всегда φ(ξ) ≥ 0, поэтому и min φ (ξ) ≥ 0. Но min φ (ξ) = 0 достигается только при всех ξ_i = 0. Это означает, что существует система неотрицательных значений x_j, которые обращают все ξ_i в нуль. Иными словами, значения x_j (j = 1, ..., n) удовлетворяют системе (54). Справедливо также и обратное утверждение: всякое допустимое решение х⁰_j≥ 0 (j = 1, ..., n) системы (54) придает всем ξ_i из (55) значения, равные нулю, т. е. сообщают форме (56) минимальное значение min φ (ξ) = 0.

Таким образом, для того чтобы система (54) была совместна в области допустимых решений (т. е. чтобы многогранник Q Не был пуст), необходимо и достаточно, чтобы min φ (ξ) = 0.

Заметим, что при min φ (ξ) >0 сразу можно заключить, что система (54) в области неотрицательных значений x_j (j = 1, ..., n) несовместна, т. е. не имеет ни одного допустимого (а тем более допустимого базисного) решения.

Итак, для отыскания допустимого решения исходной задачи линейного программирования следует минимизировать вспомогательную форму φ (ξ). От найденного допустимого решения можно теми же приемами симплекс-метода перейти к допустимому базисному решению, а затем уже перейти к решению исходной задачи (см., например, [6]).