
6.6. Угловые точки и выпуклые комбинации
Вектор X, принадлежащий выпуклому множеству V, называют крайней или угловой точкой или вершиной V, если для любых векторов X(1) и X(2) из V при 0≤λ≤1 из того, что X = (1 - λ)X(2) + λX(1), следует, что X = X(1) = X(2). Иначе, X - крайняя (угловая) точка множества V, если X нельзя представить в виде выпуклой комбинации каких-либо двух других точек из V, от нее отличных.
Геометрически это означает, что крайняя точка не может лежать внутри какого-либо отрезка, принадлежащего множеству V.
Крайними точками отрезка являются его концы, треугольника - его вершины, пирамиды - точки пересечения ребер. Каждая точка границы круговой области является крайней. Заметим, что область, не являющаяся замкнутой (например, внутренность круга без границы), может не иметь крайних точек.
Перенесем рассмотренное нами определение выпуклой комбинации двух векторов (точек) на общий случай. Вектор X из R(n) называют выпуклой комбинацией векторов X(1), ..., X(l), если его можно представить в виде линейной комбинации
X = λ1X(1) + λ2X(2) + ... + λlX(l) (39)
с неотрицательными коэффициентами λ1, λ2, ..., λl, дающими в сумме единицу:
λ1 + λ2 + ... + λl = 1.
Так, например, линейная комбинация *
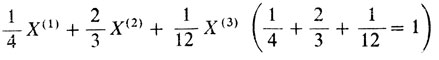
является выпуклой. В то же время не является выпуклой комбинация
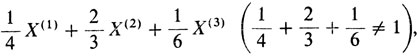
а также
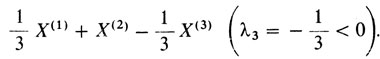
Зададим в R(n) векторы X(1), ..., X(l) и рассмотрим всевозможные их выпуклые комбинации. Множество всех таких векторов (39) называют выпуклой оболочкой заданных векторов X(1), ..., X(l).
Так, например, выпуклой оболочкой двух векторов является отрезок X = (1 - λ)X(1) + λ1X(2); выпуклой оболочкой трех векторов (не принадлежащих одному отрезку) - треугольник; выпуклой оболочкой четырех, не лежащих в одной плоскости (некомпланарных) векторов,- тетраэдр (см. рис. 18).
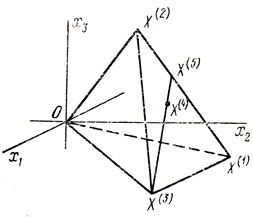
Рис. 18
В общем случае выпуклую оболочку конечного числа векторов X(1), ..., X(m) называют выпуклым многогранником (если она ограниченная) или выпуклой многогранной областью (если она неограниченная) (рис. 19). Так, например, выпуклой оболочкой векторов X(1) = (1, 0, 0), X(2) = (0, 1, 0), X(3) = (0, 0, 1), X0 = (0, 0, 0) оказывается тетраэдр с вершинами в этих точках.
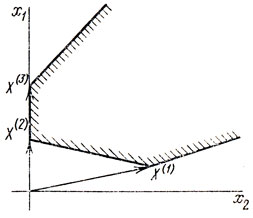
Рис. 19
Его можно задать также линейными неравенствами x1≥0, x2≥0, x3≥0, x1 + x2 + x3≤1.
Эта возможность неслучайна. Немецкий математик Герман Вейль доказал, что оба определения выпуклого многогранника (как непустого пересечения конечного числа полупространств или как выпуклой оболочки конечного числа векторов) эквивалентны.
Можно проверить, что выпуклая оболочка сама по себе является выпуклым телом и что каждое выпуклое тело совпадает со своей выпуклой оболочкой. В приложении к выпуклому многограннику это означает, что каждая его точка X является некоторой выпуклой комбинацией угловых точек X(1), ..., X(m) и любая выпуклая комбинация угловых точек определяет некоторую точку многогранника.
Короче говоря, выпуклый многогранник совпадает с выпуклой оболочкой всех своих крайних точек:
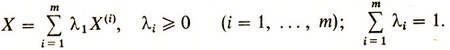
Так, например, точка X(4) (рис. 18) принадлежит отрезку, определенному векторами X(3), X(5) и поэтому X(4) = λX(3) + (1 - λ)X(5) (0≤λ≤1). По аналогичной причине X(5) = μX(1) + (1 - μ)X(2) (0≤μ≤1). Следовательно,
X(4) = λX(3) + (1 - λ)[μX(1) + (1 - μ)X(2)] = λ1X(1) + λ2X(2) + λ3(3).
где λ1 = λ; λ2 = (1 - λ)μ; λ3 = (1 - λ)(1 - μ) - неотрицательны и λ1 + λ2 + λ3 = λ + (1 - λ1)μ + (1 - λ)(1 - μ) = 1.
Последнее означает, что X(4) (произвольная точка треугольной грани) является выпуклой комбинацией угловых точек X(1), X(2), Х(3).
Рассмотрим в R(n) n + 1 точек X(j) = (a1j, a2j, ..., anj) (j = 1, ..., n+1). Говорят, что эти точки находятся в общем положении, если определитель
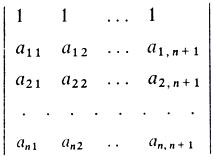
отличен от нуля. Выпуклую оболочку n+1 точек в n-мерном пространстве, находящихся в общем положении, называют n-мерным симплексом. Так, в частности, нульмерным симплексом является точка, одномерным - отрезок, двумерным - треугольник, трехмерным - тетраэдр.
В определенном смысле n-мерный симплекс является простейшим многогранником в R(n). Выпуклым многогранником V (хотя, вообще говоря, не симплексом) является совокупность точек R(n) допустимых решений задачи линейного программирования. В связи с этими обстоятельствами один из основных методов поиска оптимального значения линейной формы на множестве V получил наименование симплекс-метода
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'