
6.5. О задачах линейного программирования
Мы рассмотрели геометрический способ решения Двух задач линейного программирования. Первая из них - задача о футбольных клубах; она имеет каноническую форму - все ограничения, которым подчиняются искомые переменные (кроме условий неотрицательности), имеют вид Равенств. Вторая - задача о диете; она имеет стандартную форму - все ограничения задачи имеют вид неравенств.
И в том и в другом из рассмотренных примеров оказалось, что если оптимальное решение существует и однозначно, то оно достигается в некоторой вершине (угловой точке) многоугольника (или многогранной неограниченной области) допустимых решений. Если же оптимальное решение неоднозначно, то оно достигается во всех точках некоторой стороны (включая ограничивающие эту сторону вершины) многоугольника или области. Следовательно, коль скоро существует оптимальное решение задачи, то всегда найдется по крайней мере одна вершина многоугольника, в которой это решение достигается.
Полученный вывод имеет общий характер и сохраняет свою значимость для каждой задачи линейного программирования. Этот факт - один из основных в общей теории и о нем еще пойдет речь в дальнейшем (см. п. 6.7).
В рассмотренных выше задачах число свободных переменных, через которые удалось выразить все остальные переменные, равно двум. Именно это обстоятельство позволило построить область допустимых решений в виде многоугольника (многоугольной области) на плоскости. Если число свободных переменных равно трем, то приходится переходить в трехмерное пространство, где множество допустимых решений принимает вид многогранника (или неограниченной многогранной области). И в этом случае, в принципе, можно пытаться решить задачу геометрическим способом. Хотя практически даже в мало-мальски сложных случаях это - безнадежное предприятие.
При числе свободных переменных, большем трех, вся геометрическая наглядность исчезает и приходится обращаться к иным - универсальным методам: к методу последовательного улучшения плана (симплекс-методу), двойственному симплекс-методу (методу уточнения оценок), методу сокращения невязок или к другим методам [6].
Универсальный симплекс-метод приспособлен к решению задач линейного программирования, заданных в канонической форме.
Дадим формулировку такой задачи. Задана система
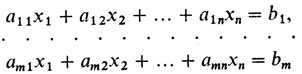 (30)
(30)m линейных уравнений с n неизвестными x1, ..., xn и линейная форма
F(X) = c0 + c1x1 + ... + cnxn (31)
относительно тех же неизвестных. Требуется среди всех неотрицательных xj≥0 (j = 1, ..., n) решений системы (30) найти такие, которые сообщают форме (31) наименьшее значение.
Систему (30) называют системой ограничений задачи. Всякое неотрицательное решение X = (x1, ..., xn); xj≥ 0 (j = 1, ..., n) называют допустимым решением или планом.
Заметим, что задача максимизации формы F (X), т. е. отыскание среди всех допустимых решений системы (30) таких, которые сообщают форме (31) наибольшее значение, сводится к задаче минимизации формы Ф (X) = - F (X). Действительно, наименьшее значение Ф(X) равно наибольшему значению F(X) взятому с противоположным знаком.
Читатель уже заметил, что среди ограничений задач, разобранных ранее, фигурировали линейные неравенства. Покажем сейчас, что ценою введения дополнительных неизвестных можно от ограничений-неравенств перейти к ограничениям-равенствам. В самом деле, пусть неравенство
α1x1 + ... + αnβn + β≥ 0 (32)
- одно из ограничений задачи. Введем новую неизвестную (обозначим ее через xn+1) с помощью уравнения
xn+1 = α1x1 + ... + αnβn + β. (33)
Ясно, что условие xn+1≥0 неотрицательности величины xn+1 эквивалентно выполнению неравенства (32). Это означает, что если набор x10, ..., xn0, xn+10 неотрицательных значений переменных x1, ..., xn, xn+1 удовлетворяет уравнению (33), то он удовлетворяет также и неравенству (32).
Справедливо и обратное утверждение: если неотрицательные величины x10, ..., xn0 удовлетворяют неравенству (32), то величина xn+10 = α1x10 + ... + αnβn0 + β, найденная из уравнения (33), окажется также неотрицательной.
Тем самым доказана эквивалентность неравенства (32) и равенства (33). Таким же способом и каждое другое ограничение-неравенство можно заменить эквивалентным ему ограничением-равенством. В итоге (хотя число неизвестных возрастет) система ограничений примет вид (30).
Выскажем в отношении системы (30) несколько общих соображений.
В курсе линейной алгебры доказывается критерий совместности системы (30) - теорема Кронекера - Капелли. Согласно этой теореме (см. [6]) система (1) совместна тогда и только тогда, когда ранги матрицы А = (a1) системы (1) и расширенной матрицы (получаемой присоединением к А столбца свободных членов) совпадают.
Пусть r = n; тогда решение системы (30) единственно и может быть найдено, например, по формулам Крамера или по методу Гаусса. Если значения x0j (j = l, ..., n) всех найденных неизвестных неотрицательны, то найденное решение X0 = (x01, ..., x0n) и является оптимальным (других решений нет). Если же среди x0j имеется хотя бы одно отрицательное, то задача решения не имеет. Следовательно, интерес представляет случай r<n. В этом случае, как известно из курса линейной алгебры, r неизвестных (их называют базисными) линейно выражаются через остальные k = n - r неизвестных (их называют свободными). Для удобства записи неизвестные всегда можно перенумеровать так, чтобы свободными были x1, x2, ..., xk, а базисными - xk+1, xk+2, ... , xk+r (k + r = n). Итак, от системы (30) мы переходим к эквивалентной ей системе
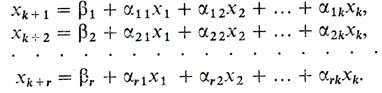 (34)
(34)Вновь повторим: эта система определяет одно из допустимых базисных решений системы (30), а именно, X = (0,..., 0, β1 ..., βr), или, иначе, x1 = x2 = ... = xk = 0; xk+j = βj (j = 1, ..., r).
Естественно теперь и форму F(X) выразить только через свободные неизвестные, заменив в (32) базисные переменные по формулам (34). В результате форма примет вид
F(X) = γ0 + γ1x1 + ... + γkxk, (35)
где γ0, ..., γk - некоторые коэффициенты.
Рассматриваемая нами задача линейного программирования требует учета лишь допустимых (неотрицательных) значений переменных. Поэтому должны выполняться неравенства xj≥ 0 (j = 1, ..., n), или, в более подробной записи,
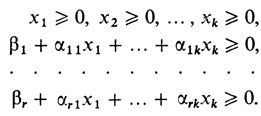 (36)
(36)Таким образом, отправляясь от системы (30) линейных равенств относительно n неизвестных, приходим к системе и линейных неравенств относительно k. неизвестных. В итоге возникает следующая математическая задача.
Дана система (36) из n линейных неравенств относительно к неизвестных x1, ..., xk и линейная форма (35) относительно тех же неизвестных. Среди всех решений (36) требуется найти такие, которые сообщают форме (35) наименьшее значение.
Остается вспомнить, что возникшая задача является также задачей линейного программирования, но в стандартной форме (все ограничения - неравенства). Итак, от задачи линейного программирования в канонической форме можно перейти к ее заданию в стандартной форме, выразив базисные переменные (включая минимизируемую форму) через свободные. От стандартной формы задания можно перейти к канонической путем введения дополнительных переменных так, как это указано выше.
Возникают две возможности для геометрической интерпретации задачи линейного программирования. Можно оставаться в n-мерном пространстве R(n) переменных x1, x2, ..., xn, либо перейти в k-мерное пространство R(k) (k<n) свободных переменных x1, x2, ..., xk.
Для этой второй интерпретации - все готово. Действительно, уже известно, что каждое из неравенств (36) определяет в R(k) некоторое полупространство, а совокупность всех неравенств - выпуклый многогранник (или выпуклую многогранную область) Q. Первые к неравенств системы (36) указывают на то, что многогранник лежит в положительном ортанте.
Далее рассматривают всевозможные гиперплоскости γ0 + γ1x1 + γ2x2 + ... + γnxn = С равных значений формы F(X) пересекающие многогранник Q допустимых решений. При этом выделяют те точки, которые отвечают наименьшему значению С. Далее доказано, что среди таких точек всегда найдется по крайней мере одна вершина (точное определение см. ниже) многогранника Q.
Перейдем теперь к геометрической интерпретации задачи линейного программирования в пространстве R(n).
Пусть, например, Х(1) = (x(1)1, ..., x(1)n) и X(2) = (x(2)1, ..., x(2)n) -два каких-либо допустимых решения системы ограничений (1). Это значит, что при подстановке этих решений в систему (1) возникнут два тождества. Запишем их в матричном виде:
AX(1) = B, AX(2) = B. (37)
Составим линейную комбинацию
X = (1 - λ)X(1) + λX(2)
(38)
этих решений с коэффициентами α1 = 1 - λ, α2 = λ при произвольном значении λ между нулем и единицей (0≤λ≤1). Такую линейную комбинацию называют выпуклой.
Если сравним (38) с формулой (19) для радиус-вектора r произвольной точки отрезка, концы которого определены векторами r1 и r2, то обнаружим их полное совпадение. И это не случайно: каждое из решений X(1) и X(2) - это n-мерные вектор-столбцы, а конец вектора X пробегает (при 0≤λ≤1) весь отрезок, соединяющий X(1) и X(2).
Подстановкой в (30) убедимся, что X также является решением этой системы:
AX = A(λX(2) + (1 - λ)X(1)) = λAX(2) + (1 - λ)AX(1).
Но в силу (37)
AX = λB + (1 - λ) В = В.
К тому же X - решение допустимое (X ≥ 0), так как для каждой из координат справедливо xi = λxi(2) + (1 - λ)xi(1) ≥ 0 (i = 1, ..., n) в силу того, что xi(1) ≥ 0, xi(2) ≥ 0, λ > 0, 1 - λ ≥ 0. Тем самым доказано, что множество V всех допустимых решений задачи линейного программирования в пространстве Rn выпукло.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'