
6.4. Задача о спортивном рационе
Одной из первых задач, решенных методами линейного программирования, явилась задача о диете*, рассмотренная американскими математиками Стигнером в 1945 г. и (независимо от него) Купмансом в 1947 г.
Вот ее постановка. Известно, что для сохранения здоровья и работоспособности человек должен потреблять в сутки некоторое количество питательных веществ: белков, жиров, углеводов, витаминов и т. д. Специальные требования (например, ограничение количества жиров и углеводов) предъявляются к составлению рациона представителей различных видов спорта. Требования основаны на рекомендациях специалистов (врачей, тренеров). Впрочем, рационально питаться надлежит не только спортсменам. Поэтому дальнейшие рассуждения носят общий характер.
Запасы питательных веществ (β1, β2, ..., βm в различных продуктах π1, π2, ..., πn различны. Обозначим через aij запасы (в некоторых единицах) питательного вещества вида βi в продукте πj. Из величин aij можно составить матрицу A = (aij) из m строк и n столбцов.
Предположим далее, что стоимость некоторой единицы продукта πj составляет cj (j = 1, ..., n), а минимальная норма (например суточная) питательного вещества βi выражена числом bi (i = 1, ..., m).
Обозначим через xj (j = 1, ..., n) количество продукта πj, приобретенного для рациона (подразумевается, что вся приобретаемая пища потребляется). В этом случае общие запасы питательного вещества βi во всех видах продуктов составят сумму
ai1x1 + ... + aijxj + ... + ainxn.
Этот запас не должен быть меньше минимальной нормы bi, что приводит к m неравенствам
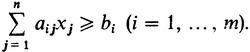 (28)
(28)При этом общая стоимость приобретенных продуктов составит
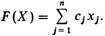 (29)
(29)Естественно, что каждая из величин xj не может быть отрицательной, т. е. xj≥0, так как продукт πj, либо приобретается в количестве xj, либо вовсе не входит в рацион.
Таким образом, реальная задача о наиболее дешевом и приемлемом по минимальным нормам рационе приводит нас к следующей математической задаче (модели).
Задана система (28) из m линейных неравенств с n неизвестными x1, ..., xn. Требуется среди всех неотрицательных решений системы (28) найти такое, которое сообщает линейной форме (29) от этих же переменных наименьшее значение (минимизирует форму F(X)).
Это - типичная задача линейного программирования, заданная в так называемой стандартной форме (ограничения (28) имеют вид неравенств). Используем векторную запись. Введем, кроме матрицы A, еще вектор-столбцы независимых и свободных членов
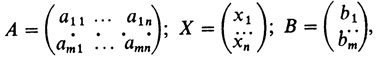
а также вектор-строку C = (c1, ..., cn) из коэффициентов формы F(X).
Использовав правило умножения матрицы A на вектор-столбец X, а также вектор-строки C на столбец B, мы можем записать кратко систему ограничений и форму F(X) в виде AX≥B, F(X) = CX, а требование неотрицательности в виде X≥0.
Линейное программирование располагает универсальными методами решения поставленной и аналогичных по математической форме задач. В частности и для задач, в которых все ограничения имеют вид точных равенств (как, например, в задаче о футбольных клубах или в задаче о назначениях).
Первый из таких методов - метод разрешающих множителей - был предложен Л. В. Канторовичем в 1939 г. и усовершенствован им и М. К. Гавуриным в 1940 г. К 1949 г. относится публикация первой в США работы по общим проблемам линейного программирования. В ней Дж. Данциг изложил получивший широкое признание симплекс-метод решения общей задачи линейного программирования. Оставляя пока симплекс-метод вне рассмотрения, попытаемся уяснить смысл математической модели задачи о рационе и проведем необходимый анализ. Ограничимся простейшим вариантом, в котором фигурируют пять питательных веществ (m = 5) и два типа продуктов (n = 2).
Всем известным по условию величинам (aij и bi) придадим конкретные числовые значения. Они сведены в табл. 8 и носят чисто иллюстративный характер.
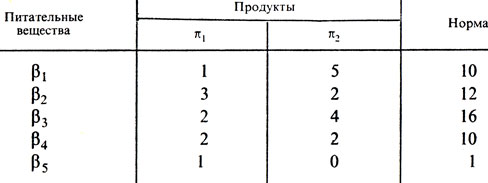
Таблица 8
Ограничения (28), условия неотрицательности переменных и минимизируемая форма примут вид
x1 + 5x2≥10, (I)
3x1 + 2x2≥20, (II)
2x1 + 4x2≥16, (III)
2x1 + 2x2≥10, (IV)
x1≥1, (V)
x2≥0, (VI)
F(X) = 2x1 + 3x2
(неравенство x1≥0 является следствием неравенства x1≥1 и потому не включено в эту систему).
На рис. 17 показана область Q допустимых решений, определяемая системой линейных неравенств (I)-(VI), и линии уровня минимизируемой формы F.
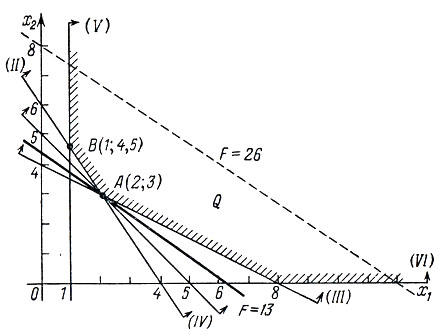
Рис. 17
Видно, что наименьшее значение достигается формой F(X) в точке A (2, 3) - одной из вершин области Q. Следовательно, наиболее дешевый рацион стоит F (A) = 13 денежных единиц и обеспечивается закупками продуктов π1 и π2 в объеме x1 = 2, x2 = 3 единиц соответственно.
Отметим, что в рассматриваемом примере область Q допустимых решений неограниченно простирается вверх. Это означает, что в области Q имеются точки с координатами (x1, x2), доставляющие форме F(X) сколь угодно большие значения.
Последнее свидетельствует о том, что питание можно организовать сколь угодно дорого.
Изменим стоимость продуктов π1 и π2, положив их равными 2 и 3 единицам соответственно. В этом случае надлежит минимизировать форму Ф(X) = 3x1 + 2x2. Линии уровня этой формы параллельны стороне AB области Q. Поэтому наименьшее значение F(X) достигается в каждой точке стороны AB.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'