6.3. Некоторые основные понятия и факты

Рассмотрим на плоскости, где введена система декартовых координат, две точки M₁, M₂ и их радиус-векторы r₁ = 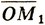, r₂ = 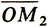(рис. 13). Разность векторов r₂ и r₁ равна r₂ - r₁ = 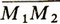. Предположим, что λ - произвольное число, удовлетворяющее неравенству 0≤λ≤1. Если вектор 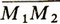умножить на скаляр λ, то получится вектор λ 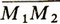= s, коллинеарный 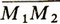, направленный в ту же сторону, но имеющий длину, меньшую чем 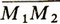. Ясно, что если совместить начало вектора s с точкой M₁, то его конец M попадет внутрь отрезка M₁M₂. При λ = 0 точка M совпадает с M₁, при λ = 1 - с точкой M₂. При любом 0≤λ≤1 радиус-вектор r точки M равен сумме: r = r₁ + s₁ = r₁ + λ(r₂ - r₁). Итак, радиус-вектор r любой точки M, лежащей на отрезке между M₁ и M₂, находится по формуле

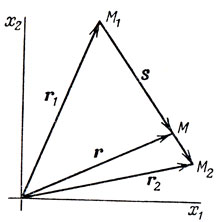
Рис. 13

Наши рассуждения, а значит и формула (18), без всяких изменений переносятся со случая плоскости (размерность n = 2) на случай трехмерного пространства (n = 3). Поэтому естественно, перейдя к рассмотрению пространства произвольного числа n измерений, считать, что радиус-вектор r произвольной точки отрезка M₁M₂ находится по той же формуле (18).

На плоскости каждая из точек, например M₁ и M₂, задается двумя координатами: M₁(x₁⁽¹⁾, x₂⁽¹⁾); M₂(x₁⁽²⁾, x₂⁽²⁾). Те же координаты имеют соответствующие векторы r₁ = 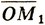= {x₁⁽¹⁾, x₂⁽¹⁾} и r₂ = 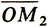= {x₁⁽²⁾, x₂⁽²⁾}. Координаты вектора r = {x₁, x₂} (и точки M) находятся по формуле (18), которая при переходе к координатной записи приводит к двум соотношениям:

В пространственном случае (n = 3) добавляется еще одно соотношение для третьей координаты:

В n-мерном пространстве точки M₁ {x₁⁽¹⁾, ..., x₁⁽ⁿ⁾), M₂ (x₁⁽²⁾, ..., x_n⁽²⁾) задаются каждая п координатами, а координаты точки M(x₁, ..., x_i, ..., x_n) определяются из n соотношений

или из одного векторного соотношения

Множество всех таких точек M назовем отрезком M₁M₂ в n-мерном пространстве.

Совокупность точек пространства T называют выпуклым телом (фигурой), если вместе с двумя любыми его точками M₁ и M₂ к этой совокупности принадлежат все точки отрезка M₁M₂.

Примерами выпуклых плоских тел могут служить круг, круговой сектор, сегмент, любой правильный многоугольник. В пространстве - это шар, конус, а также призма и пирамида, в основании которых лежат правильные многоугольники. На рис. 14, а представлена выпуклая фигура, на рис. 14, б - фигура, не являющаяся выпуклой.

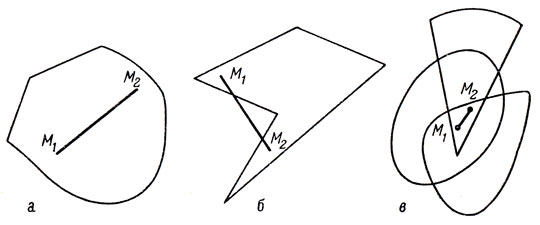
Рис. 14

Под пересечением тел (фигур) понимают множество точек, принадлежащих каждому из этих тел. Пересечение любого числа выпуклых тел вновь является выпуклым телом. Убедимся в этом (см. рис. 14, в). Выберем любые две точки M₁ и M₂, принадлежащие пересечению. Эти точки принадлежат каждому из пересекающихся тел. Но каждое из них по условию выпукло и, значит, каждое содержит весь отрезок M₁M₂. В силу этого отрезок M₁M₂ полностью принадлежит и их пересечению. Последнее означает, что пересечение - выпуклое тело.

Зададим в плоскости некоторую прямую уравнением: a₀ + a₁x₁ + a₂x₂ = 0. Она делит всю плоскость на две части - на две полуплоскости. Отметим далее на плоскости пару точек M₁ и M₂ и установим признаки, по которым можно узнать, принадлежат ли отмеченные точки одной и той же или разным полуплоскостям. Бот эти очевидные необходимые и достаточные признаки:

Если точки M₁ и M₂ принадлежат одной полуплоскости, то отрезок M₁M₂, их соединяющий, не пересекает заданной прямой. Если отрезок M₁'M'₂ соединяющий точки M'₁ и M'₂, пересекает эту прямую, то точки M'₁ и M'₂ лежат в разных полуплоскостях (см. рис. 15).

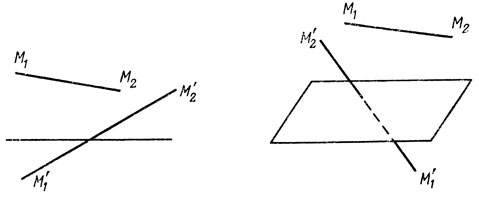
Рис. 15

Аналогичные признаки имеют место в трехмерном пространстве: они позволяют выяснить, лежат ли точки по одну или по разные стороны от заданной плоскости a₀ + a₁x₁ + a₂x₂ + a₃x₃ = 0. Без изменения признаки переносятся далее на общий случай n-мерного пространства. Здесь рассматривается геометрическое место точек (так называемая гиперплоскость), задаваемое линейным относительно x₁, ..., x_n уравнением

Оказывается, что совокупность всех точек n-мерного пространства T, не лежащих на гиперплоскости (20), можно разбить на две части так, что окажутся выполненными следующие условия: отрезок, соединяющий любую пару точек из одной и той же части, не пересекает гиперплоскость (20); отрезок, соединяющий любую пару точек из разных частей, пересекает гиперплоскость (20).

Убедимся в этом. Для сокращения записи ограничимся плоским случаем (n = 2). Для произвольного n рассуждения остаются теми же. Зададим прямую

Линейная форма, равная левой части этого уравнения, имеет вид

В точках плоскости, не лежащих на прямой (21), форма Ф≠0. Разобьем всю плоскость на две части и обозначим их через Т⁺ и Г^-. К части Т⁺ отнесем все точки плоскости, в которых Ф>0, а к части Г^- - все точки, где Ф<0. Проверим теперь, что для каждой из частей Т⁺ и Г^- справедливо наше утверждение.

Пусть M₁(x₁⁽¹⁾, x₂⁽¹⁾) и M₂(x₁⁽²⁾, x₂⁽²⁾) - две точки из одной и той же части, например Т⁺. Тогда

Умножим (23) и (24) соответственно на числа 1-λ>0 и λ>0. Получим:

Но x₁ = (1-λ)x₁⁽¹⁾ + λx₁⁽²⁾ и x₂ = (1-λ)x₂⁽¹⁾ + λx₂⁽²⁾ при 0≤λ≤1 суть координаты произвольной точки M отрезка M₁M₂. Неравенство (25) можно записать в виде Ф(M) = (1-λ)Ф(M₁) + λФ(M₂). При этом результат Ф(M)>0 означает, что точка M, и следовательно весь отрезок M₁M₂ принадлежат части Т⁺. Теперь предположим, например, что Ф(M₁)>0, а Ф(M₂)<0, т. е. что M₁ и M₂ принадлежат различным частям. Точка M окажется на прямой (21), если Ф(M) = 0, т. е. при (1-λ)Ф(M₁) + λФ(M₂) = 0. Отсюда находим

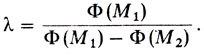(26)

По условию выбора точек Ф(M₁)>0, Ф(M₂)<0, следовательно λ, найденное из (26), удовлетворяет неравенствам 0≤λ≤1 и поэтому определяет точку M отрезка M₁M₂, принадлежащую в то же время прямой (21). Этим доказано, что отрезок M₁M₂ пересекает прямую (21).

Итак, заданием прямой (21) вся плоскость Т разбивается на две части - на две полуплоскости. Каждая из них ограничена прямой (21), которую мы условимся относить к каждой из полуплоскостей.

Если теперь обратиться к гиперплоскости (20), то, перенося рассуждения на этот общий случай, можно заключить:

Гиперплоскость (20) делит пространство на две части - полупространства. В каждом из полупространств форма Ф = a₀ + a₁x₁ + ... + a_nx_n сохраняет свой знак. В различных полупространствах знак Ф различен. Следовательно, любая гиперплоскость a₀ + a₁x₁ + ... + a_nx_n = C, где C = const, целиком лежит либо в одном, либо в другом полупространстве в зависимости от знака C.

Покажем, что полуплоскость (полупространство), ограниченная любой прямой (21) (гиперплоскостью (20)), является выпуклым телом. Мы уже видели, что если точки M₁ и M₂ принадлежат одной и той же полуплоскости (полупространству), то Ф(M₁) и Ф(M₂) имеют одинаковые знаки. Тот же знак имеет Ф(M) для любой точки M отрезка M₁M₂. Это означает, что той же полуплоскости (полупространству) принадлежит и весь отрезок M₁M₂.

Рассмотрим теперь произвольное линейное неравенство относительно переменных x₁ и x₂. Его всегда можно записать в виде

Областью решений этого неравенства назовем совокупность точек плоскости, чьи координаты удовлетворяют этому неравенству.

Убедимся, что областью решений линейного неравенства является полуплоскость. Для этого перейдем от неравенства (27) к равенству a₀ + a₁x₁ + a₂x₂ = 0. Это уравнение определяет прямую на плоскости. Уже известно, что прямая делит плоскость на две полуплоскости. В каждой из точек одной из полуплоскостей F = a₀ + a₁x₁ + a₂x₂≥0. Эта полуплоскость и является областью решения неравенства (27).

В качестве примера рассмотрим неравенство

Прямая 2 - x₁ - x₂ = 0 разбивает всю плоскость на две части. Областью решений неравенства (1) является та из полуплоскостей, которой принадлежит начало координат. Другая полуплоскость является областью решений неравенства 2 - x₁ - x₂≤0.

По аналогии с изложенным областью решений линейного неравенства

относительно n переменных x₁, ..., x_n является некоторое полупространство п-мерного пространства.

Естественно назвать областью решений системы линейных неравенств множество точек пространства, координаты которых удовлетворяют каждому из неравенств системы.

Так как каждое из неравенств системы определяет некоторое полупространство, то областью решений системы неравенств

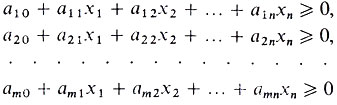
является пересечение m полупространств. Это пересечение оказывается пустым множеством, если система неравенств несовместна.

Пересечение (если оно непусто) любого числа полупространств называется выпуклым многогранником (или выпуклой многогранной областью, если оно не ограничено).

Итак, областью решений совместной системы линейных неравенств является выпуклый многогранник (или неограниченная выпуклая многогранная область). Многогранник ограничен гиперплоскостями, уравнения которых получаются из неравенств системы переходом к равенствам.

Теперь в качестве иллюстрации снова рассмотрим систему ограничений (I)-(VI) поставленной ранее задачи и решим ее геометрическим методом.

Эта система неравенств определяет выпуклый многоугольник P, лежащий в первой четверти и изображенный на рис. 16.

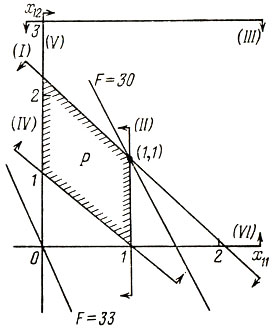
Рис. 16

Среди точек многоугольника P требуется найти точки, в которых форма S(X) из (15) принимает наименьшее значение. С этой целью рассмотрим линии уровня формы S(X). Для S(X) = 33 линия уровня имеет уравнение 33 = 33 - 2_x11 - x₁₂, т. е. x₁₂ = - 2x₁₁.

Эта прямая проходит через начало координат с угловым коэффициентом k = - 2 и показана на рис. соответствующей линией. Всякая другая линия уровня S (X) = C параллельна изображенной прямой.

Выделим из линий уровня S(X) ту, которая отвечает наименьшему из возможных значений и в то же время пересекает многоугольник P. Этой линией (показана на рис. 16) является та, которая проходит через вершину P - точку (1, 1). Она отвечает значению S (X) = 33 - 2 - 1 = 30. Таким образом, наименьшее значение затрат формы min S(X) = 30 и определяется значениями переменных

Это означает, что оптимальным является план, согласно которому из центра A₁ в клубы B₁ и B₂ направляется по одному футболисту. Из центра A₂ в клубы B₂ и B₃ переводятся соответственно двое и один спортсмен.

Прежде чем формулировать общие свойства решений задач, подобных рассмотренной выше (или задаче о назначениях), разберем еще один пример. Забегая вперед, отметим, что в нем содержится новый элемент: множеством допустимых решений в этом примере оказывается не выпуклый многогранник (или многоугольник, как в последней задаче), а неограниченная выпуклая многогранная область.