6.7. Угловые точки и допустимые решения

Почему же угловые точки выпуклого многогранника заслужили столь пристальное внимание? Ответ заключен в следующем весьма важном факте (было обещано его доказать).

Всякая линейная форма F(X) = γ₀ + γ₁x₁ + ... + γ_nx_n, значения которой рассматриваются в точках некоторого выпуклого многогранника Q, достигает своего наименьшего (наибольшего) значения в одной из его угловых точек. Если F (X) принимает наименьшее (наибольшее) значение более, чем в одной угловой точке, то она принимает то же значение в каждой точке, являющейся их выпуклой комбинацией.

В самом деле, по условию значения формы F (X) рассматриваются в точках многогранника Q. Обозначим через X⁽¹⁾, ..., X⁽ⁿ⁾ его угловые точки (по определению выпуклого многогранника их конечное число). Допустим, что наименьшее значение F (X) достигает в некоторой точке X⁰ многогранника Q; иными словами, F(X⁰) = minF(X) = F^*. Значит, для любой иной точки X из Q справедливо неравенство F (X) ≥ F (X⁰). Если X⁰ - одна из угловых точек, то первая часть утверждения уже доказана. Предположим, что X⁰ - не угловая точка. Но тогда X⁰ является выпуклой комбинацией угловых точек:

X⁰ = λ₁X⁽¹⁾ + ... + λ_mX^(m),

λ_k≥0 (k = 1, ..., m); λ₁ + ... + λ_m = 1.

В силу свойств линейности формы F(X) ее значение в точке X⁰

оказывается выпуклой комбинацией значений в угловых точках. Проверяется этот факт непосредственным вычислением. Выберем наименьшую из величин F(X⁽¹⁾), ..., F (X^(m)); пусть это будет F(X^(k)). Тогда F(X⁽ⁱ⁾)≥F(X^(k)) (i = 1, ..., m) и из (40) вытекает неравенство

Однако по предположению F(X⁰)≤F(X) для любой точки X из Q, и, конечно, F (X⁰) ≤ F (X^(k)). Остается предположить равенство F (X⁰) = F (X^(k)), т. е. что наименьшее значение достигается по крайней мере в угловой точке X^(k). Этим первая часть утверждения доказана.

Перейдем к доказательству второй части. Пусть F (X) достигает наименьшего значения F^* в каждой из угловых точек (нумерация несущественна) Х⁽¹⁾, ..., Х^(l) Составим их произвольную выпуклую комбинацию

Тогда значение формы F(X) в точке X оказывается также наименьшим:

Утверждение полностью доказано.

Мы приходим к выводу, что оптимальные значения формы F(X) на многограннике Q допустимых решений системы ограничений (30) задачи линейного программирования следует искать среди значений в угловых точках Q.

Но как находить эти угловые точки? Возможно ли их выявить, опираясь лишь на рассмотрение системы (30)?

Ответ на поставленный вопрос положительный: угловые точки выявляются вместе с нахождением допустимых базисных решений системы (30). Более точный ответ дает следующее утверждение.

Каждое допустимое базисное решение системы ограничений (30) задачи линейного программирования (например, решение x₁ = ... = x_k = 0; x_k+1 = β₁, ..., x_k+r = β, уравнений (34)) определяет единственную угловую точку X_. = (0, ..., 0, β₁, ..., β_r) многогранника Q. Обратно, каждая угловая точка X_. многогранника Q определяет некоторое (вообще говоря, не единственное) допустимое базисное решение системы (30).

Это утверждение (доказательство см. в [17]) позволяет оценить верхнюю границу возможного числа угловых точек многогранника Q: угловых точек не больше, чем имеется в системе (30) допустимых базисных решений.

Будем считать, что ранг r системы (30) совпадает с числом m уравнений. В ином случае можно сохранить в системе только r линейно независимых уравнений, а остальные отбросить. Ранее отмечено (см. с. 114), что для задач линейного программирования интересен случай r<n. В линейной алгебре доказано, что разрешить систему (30) относительно неизвестных (базисных) x_k+1, ..., x_k+r и выразить их через свободные неизвестные x₁, ..., x_k можно тогда и только тогда, когда в матрице

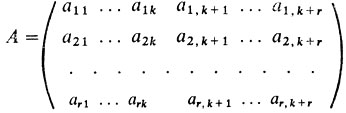
минор, образованный последними r столбцами (коэффициентами при базисных переменных), отличен от нуля.

Подобно этому выразить любые иные r базисных неизвестных x_σ1, ..., x_σr через остальные - свободные неизвестные x_σr+1, ..., x_σr+k можно лишь тогда, когда минор матрицы A, составленный из столбцов коэффициентов, отвечающих этим базисным переменным, отличен от нуля:

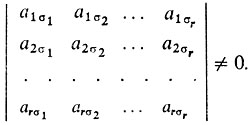
Легко подсчитать, что всех миноров порядка r в матрице А столько, сколько можно составить сочетаний из n столбцов по r, а именно:

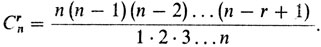
Следовательно, существует не более, чем C^r_n различных базисных решений (ведь не все миноры порядка r матрицы А отличны от нуля). Кроме того, не всякое базисное решение является допустимым. Поэтому угловых точек заведомо не больше, чем C_n^r. При r = 5, n = 10, C₁₀⁵ = 756. О примерном числе угловых точек можно составить представление по таблице:

Как видно, число угловых точек велико даже для относительно малых m и n. В практических задачах значения тип могут достигать нескольких сотен. Поэтому поиск тех угловых точек, которые доставляют форме F (X) оптимальное значение путем простого перебора, хотя и осуществим теоретически (ведь их конечное число!), практически является предприятием бесперспективным.

К счастью, существует хорошо организованный порядок перебора угловых точек. При этом порядке переход от одной угловой точки к следующей сопровождается уменьшением значения минимизируемой формы, и процесс поиска достаточно быстро (в среднем за m шагов, m - число линейно независимых ограничений) завершается. Такой порядок доставляет нам симплекс-метод. Опишем идею этого метода.