5.5. Прыжок в XXI век?

Феноменальный прыжок на 890 см американского спортсмена Р. Бимона - яркое достижение XIX Олимпиады 1968 года в Мехико. Прыжок этот назвали прыжком в XXI век.

В последние годы многим спортсменам удалось прыгнуть на 830-870 см. Правда, подобные результаты все еще редкость: их бывает не более четырех в год.

Попытаемся, хотя бы приближенно, оценить вероятность того, что рекорд Бимона будет превзойден еще в этом веке.

Любой прыжок за 830 см будем называть "удачным" прыжком. За всю историю легкой атлетики зарегистрировано около 30 удачных прыжков. Первый удачный прыжок (831 см) совершил в 1962 г. советский спортсмен И. Тер-Ованесян. С 1962 по 1982 гг. зарегистрировано пятнадцать удачных прыжков (кроме прыжка Бимона). Вот их реестр, составленный на основе справочника по легкой атлетике [12]:

Введем в рассмотрение случайную величину L, равную округленной до ближайшего десятка (в меньшую сторону) длине прыжка. Разобьем весь диапазон отмеченных значений L на интервалы (разряды) длиной в 10 см и подсчитаем число m_i значений, приходящихся на каждый i-й разряд, затем найдем статистическую вероятность p^∼_i = m_i/N, разделив m_i на общее число N = 15 отмеченных значений. Приходим к статистическом ряду:

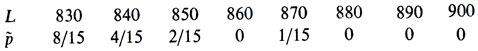
Этому статистическому ряду можно придать наглядность с помощью так называемой гистограммы (рис. 12).

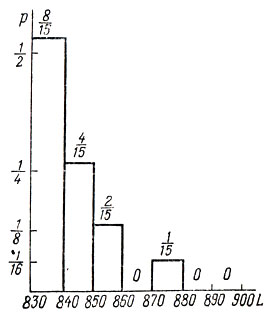
Рис. 12

Нетрудно обнаружить, что рассматриваемый ряд хорошо согласуется по различным статистическим критериям (мы лишены возможности останавливаться на этом вопросе и отсылаем читателя к литературе по математической статистике [3; 26]) со следующим теоретическим рядом распределения случайной величины X:

Отсюда следует, что вероятность "удачного" прыжка, не превосходящего рекорда Бимона, равна

Если предположить, что максимальное число "удачных" прыжков за год равно четырем, то по этой несколько завышенной оценке до конца текущего столетия можно ожидать 60 "удачных" прыжков.

Вероятность q того, что ни один из них не превзойдет рекорда Бимона, равна

Следовательно, вероятность того, что по крайней мере один из этих прыжков окажется новым мировым рекордом (т. е. превысит 890 см) составит

В действительности, как следует из' многолетних наблюдений, в год регистрируется в среднем лишь два удачных прыжка. Поэтому более реальная оценка

а вероятность побития рекорда Бимона в текущем столетии будет p = 0,375.

Итак, вероятность того, что Р. Бимон "прыгнул в XXI век", достаточно велика^*.

^* (На международных соревнованиях в Лос-Анджелесе обладатель четырех золотых медалей Олимпийских игр 1984 г. К. Льюис 18 мая 1985 г. намеревался побить рекорд Бимона. Однако новый рекорд не состоялся. Лишь в четвертой попытке Льюис улетел на 877 см, причем попутный ветер превышал допустимую норму (Советский спорт, 21 мая 1985 г.).)