5.4. Сильнее!

В этом разделе мы продолжаем знакомство с элементами корреляционного анализа и приложением его к одной из спортивных задач. Цель этого раздела математической статистики состоит в исследовании взаимосвязи между интересующими нас явлениями, точнее, в выяснении вопроса о наличии или отсутствии подобной связи. Дадим постановку задачи.

Пусть имеется система случайных величин

Над этой системой произведено n независимых наблюдений, и результаты этих наблюдений оформлены в виде таблицы Гм табл. 2), каждая строка которой содержит m значений, принятых случайными величинами X_k (k = 1, ..., m) в одном наблюдении.

Таблица 2

Числа, занесенные в эту таблицу и занумерованные двумя индексами, представляют собой зарегистрированные результаты наблюдений. Первый индекс обозначает номер наблюдения, второй - номер случайной величины. Таким образом, x_ik - это значение, принятое случайной величиной X_k в i-м опыте.

Требуется найти оценки для числовых характеристик этой системы, а главное, найти элементы корреляционной матрицы

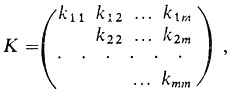
в которой k_ij = k_ji - корреляционные моменты между i-й X_i и j-й X_j случайными величинами. В силу симметричности матрицы K относительно главной диагонали в нее записывают только элементы главной диагонали и лежащие над ней, а другую - симметричную часть - в записи опускают.

Наибольший интерес представляет нормированная корреляционная матрица, состоящая из коэффициентов корреляции. По этой матрице также можно определить степень взаимосвязи случайных величин и влияние их друг на друга. Такую матрицу будем обозначать через

где r_ij = 1 - коэффициент корреляции величины X_i с самой собой, а

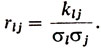
В целях определения коэффициентов корреляции по статистическим данным найдем сначала оценки для математических ожиданий

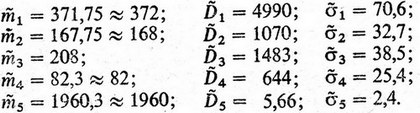
Затем вычислим несмещенные оценки для дисперсий

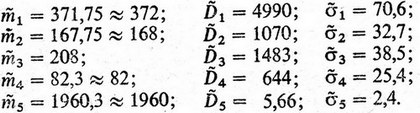
и корреляционных моментов

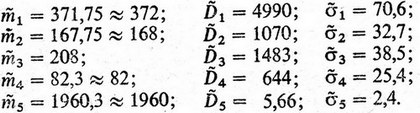
По этим данным и определяются оценки для элементов нормированной корреляционной матрицы

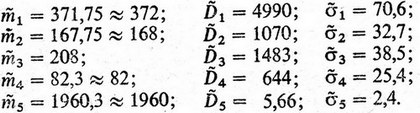
Перейдем теперь к тяжелой атлетике и используем описанный выше статистический аппарат для выявления зависимости между следующими величинами:

• X₁ - сумма тяжелоатлетического двоеборья (кг),
• X₂ - результат в рывке (кг),
• X₃ - результат в толчке (кг),
• X₄ - вес спортсмена (кг),
• X₅ - возраст спортсмена (год рождения).

В качестве исходных статистических данных рассмотрим сведения о десятке лучших спортсменов и о рекордах мира; тем самым мы как бы проведем десять экспериментов. Все данные взяты из материалов, подготовленных судьей международной категории М. Аптекарем и опубликованных в газете "Советский спорт" 19 октября 1983 г.

Сведем эти материалы в табл. 3.

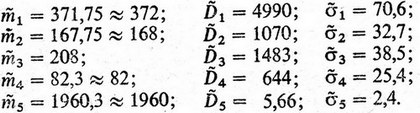
Таблица 3

Вычисляем по известным уже формулам

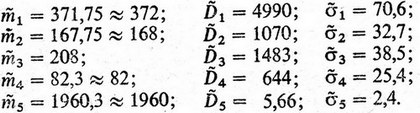
Таблица 4

Составим таблицу разностей 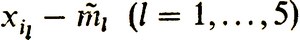(табл. 4) и их квадратов (табл. 5).

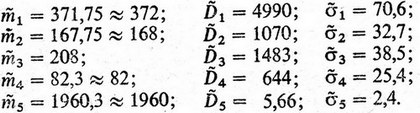
Таблица 5

Найдем корреляционные моменты:

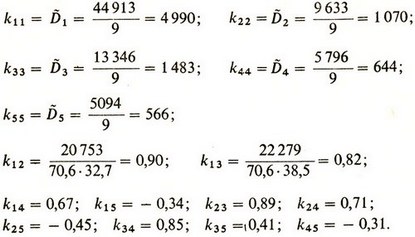
Нормированная корреляционная матрица в нашем случае выглядит следующим образом:

Легко заметить, что X₁, X₂, X₃, X₄ - достаточно сильно коррелированы между собой, в то же время год рождения почти не коррелирован, наблюдается лишь небольшое "постарение" с ростом весовой категории.