
5.3. Выше!

Интересно представить себе, какой результат покажут прыгуны с шестом в 1990 г.? Математическая статистика может нам помочь ответить (конечно, в первом приближении!) и на этот вопрос. Однако прежде чем дать на него ответ, нам необходимо ввести два понятия: системы случайных величин. и корреляционного момента.
В математической статистике часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной, а несколькими случайными величинами. В таких случаях говорят о системе случайных величин. Примером может служить система двух величин H и Q, одна из которых H - рост человека, а другая Q - его вес. Пара (H, Q) является системой случайных величин, ибо заранее (до измерений) ни точный вес, ни точный рост индивида неизвестны.
Рассмотрим теперь пару X, Y случайных величин. Пусть, по-прежнему, X принимает значения x1, ..., xn с вероятностями p1, ..., pn, а случайная величина Y - значения y1, ..., yl с вероятностями q1, ..., ql. Соответствующие центрированные случайные величины обозначим через  и
и 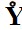 . Введем на плоскости декартову систему координат xOy и рассмотрим точку C0 с координатами x0 = mx; y0 = my. Значения (xi, yj) случайных величин (X, Y) изображаются точками, разбросанными вокруг C0.
. Введем на плоскости декартову систему координат xOy и рассмотрим точку C0 с координатами x0 = mx; y0 = my. Значения (xi, yj) случайных величин (X, Y) изображаются точками, разбросанными вокруг C0.
Важной числовой характеристикой пары случайных величин (как бы характеризующей упомянутый разброс) служит так называемый корреляционный момент Kxy величин X, Y. Корреляционным моментом Kxy случайных величин X и Y называют математическое ожидание произведения 
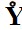 центрированных случайных величин, соответствующих X и Y:
центрированных случайных величин, соответствующих X и Y:
Kxy = M[
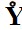 ] = M[(X - mx)(Y-my)].
] = M[(X - mx)(Y-my)].

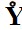 ] = M[(X - mx)(Y-my)].
] = M[(X - mx)(Y-my)].
Корреляционный момент Kxy служит характеристикой связи между X и Y. Преобразуем выражение для Kxy. С этой Целью обозначим через pij вероятность совместного появления значений X = xi, Y = yj случайных величин X и Y Всевозможными значениями произведения 
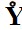 являются величины (xi - mx)(yj - my), а математическим ожиданием, т. е. корреляционным моментом, будет сумма произведений
являются величины (xi - mx)(yj - my), а математическим ожиданием, т. е. корреляционным моментом, будет сумма произведений
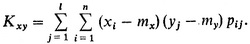
Допустим, в частности, что величины X и У независимые (см. с. 31). Тогда вероятность pij появления пары (xi, yj) равна произведению вероятностей piqj независимого друг от друга появления значений X = xi, Y = yj. В этом случае, изменив порядок суммирования, найдем
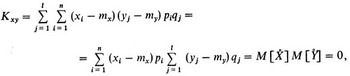
так как математическое ожидание каждой центрированной случайной величины равно нулю. Следовательно, для независимых случайных величин корреляционный момент равен нулю.
Кроме того, из формулы для Kxy можно заключить, что коль скоро значения одной из случайных величин, например X, незначительно отклоняются от своего математического ожидания, то и корреляционный момент будет мал, безотносительно к тому, сколь тесной является зависимость между X и Y.
Обычно вместо Kxy рассматривают так называемый коэффициент корреляции
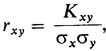
где σx, σy - среднеквадратические отклонения случайных величин X, Y.
Если корреляционный момент Kxy (или, что то же самое, коэффициент корреляции rxy) равен нулю, величины X, Y называют некоррелированными.
Независимые случайные величины всегда являются некоррелированными. Однако обратное утверждение, вообще говоря, неверно: из равенства нулю rxy еще не следует независимость X и Y.
Зависимость между случайными величинами X и У может быть весьма сложной и в явном виде не прослеживаться.
Мы остановимся на простейшем, но важном случае, когда заранее известно, что X и Y связаны линейной зависимостью (a и b - постоянные) Y = aX + b. Подсчитаем для этой зависимости коэффициент корреляции:
Kxy = M[
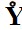 ] = M[(X - mx)(Y - my)] = M[(X - mx)(aX + b - amx - b)] = M[(X - mx)2a = aM [(X - mx)2] = aD[X].
] = M[(X - mx)(Y - my)] = M[(X - mx)(aX + b - amx - b)] = M[(X - mx)2a = aM [(X - mx)2] = aD[X].

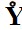 ] = M[(X - mx)(Y - my)] = M[(X - mx)(aX + b - amx - b)] = M[(X - mx)2a = aM [(X - mx)2] = aD[X].
] = M[(X - mx)(Y - my)] = M[(X - mx)(aX + b - amx - b)] = M[(X - mx)2a = aM [(X - mx)2] = aD[X].Найдем далее дисперсию величины Y:
D[Y] = D[aX + b] = D[aX] = a2D[X].
Отсюда получаем для среднеквадратических отклонений σx = √Dx, σy = √Dy аналогичную зависимость: σy = |a|σx.
Следовательно, коэффициент корреляции
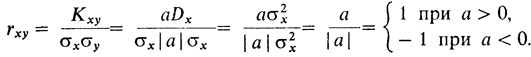
Таким образом, если зависимость между X и Y линейная, то rxy = ±1, смотря по тому, каков знак коэффициента a.
Можно доказать, что в случае произвольной случайной зависимости между X и Y коэффициент корреляции подчиняется неравенствам -1≤rxy≤1.
Действительно, введем в рассмотрение случайную величину U = σyX ± σxY - линейную комбинацию величин X и У с коэффициентами σy; ± σx. Вид случайной зависимости между самими величинами X и У нам неизвестен. Подсчитаем дисперсию D[U]. С этой целью непосредственно убедимся, что дисперсия суммы X' + Y' двух случайных величин равна сумме их дисперсий, сложенных с удвоенным значением корреляционного момента:
D [X' + Y'] = D [X'] + D [Y'] + 2Kxy.
Проверим это. Введем обозначение Z = X' + Y'. Так как математическое ожидание суммы случайных величии равно сумме их математических ожиданий: mz = mx' + my', то Z - mz = X' - mx' + Y - my', т. е. для центрированных величин возникает та же связь: 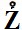 =
=  +
+ 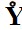 . Поэтому
. Поэтому
D [X' + Y'] = M [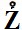 2] = M[
2] = M[ '2 +
'2 + 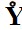 '2 + 2
'2 + 2 '
'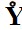 '] = M [
'] = M [ '2] + M[
'2] + M[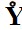 '2] + 2M[
'2] + 2M[ '
'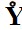 '] = Dx + Dy + 2Kxy.
'] = Dx + Dy + 2Kxy.
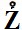 2] = M[
2] = M[ '2 +
'2 + 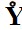 '2 + 2
'2 + 2 '
'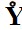 '] = M [
'] = M [ '2] + M[
'2] + M[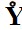 '2] + 2M[
'2] + 2M[ '
'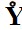 '] = Dx + Dy + 2Kxy.
'] = Dx + Dy + 2Kxy.Тем самым получен требуемый результат.
Теперь остается положить X' = σyX, Y = σxY и записать, что
D [σyX ± σxY] = D [σyX] + D [σxY] ± 2M [σxσy
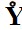 ] = σy2Dx + σx2Dy ± 2σxσyKxy.
] = σy2Dx + σx2Dy ± 2σxσyKxy.

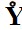 ] = σy2Dx + σx2Dy ± 2σxσyKxy.
] = σy2Dx + σx2Dy ± 2σxσyKxy.Но дисперсия произвольной случайной величины неотрицательна:
σy2Dx + σx2Dy ± 2σxσyKxy≥0.
Так как Dx = σx2; Dy = σy2, то
2σx2σy2 ± 2σxσyKxy≥0,
σxσy ± Kxy≥0, или ±Kxy/σxσy≥0,
т. е. |rxy|≤1, или - 1≤rxy≤1.
Изобразим в системе, координат xOy полученные из наблюдений пары значений (xi, yj) в виде соответствующих точек. По взаимному расположению этих точек можно судить, в первом приближении, о наличии корреляции (в частности линейной) между величинами X и Y.
В общем случае, как уже доказано, коэффициент корреляции изменяется в границах: -1≤rxy≤1. Если при этом rxy>0, говорят о положительной корреляции, а если rxy<0 - об отрицательной. Факт положительной корреляции между случайными величинами означает, что при возрастании одной из них другая имеет тенденцию в среднем также возрастать, в случае отрицательной корреляции при возрастании одной величины другая имеет тенденцию в среднем убывать. В примере с ростом и весом человека мы сталкиваемся, естественно, с положительной корреляцией. Естественно также, что чем больше по абсолютной величине коэффициент корреляции, тем существует более тесная связь между соответствующими случайными величинами.
Теперь мы готовы вернуться к вопросу, поставленному в начале этого параграфа. С этой целью попробуем построить линейную зависимость между рекордными результатами и годами, в которые эти результаты были достиг нуты, найти коэффициент корреляции и тем самым определить надежность прогноза. Выпишем таблицу мировых рекордов по прыжкам с шестом [12]:

Для наглядности можно данные из приведенной таблицы изобразить графически (см. рис. 11).
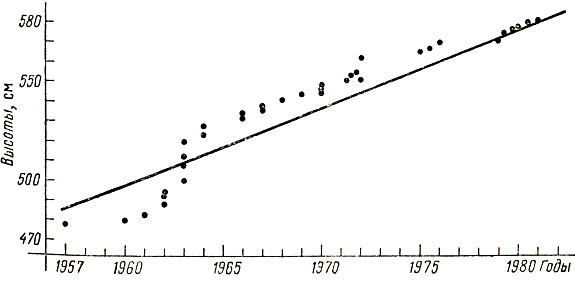
Рис. 11
Для построения линейной зависимости рекордного результата от соответствующего года - года достижения этого результата - воспользуемся методом наименьших квадратов. Идея метода наименьших квадратов, грубо говоря, состоит в выборе такой прямой, сумма квадратов расстояний до которой от экспериментально найденных точек минимальна. Фактически мы хотим построить линейную функцию, которая как бы сглаживает экспериментально установленную (в действительности нелинейную) зависимость между случайными величинами X и Y.
Не вдаваясь в технические подробности вычисления коэффициентов a и b, определяющих такую прямую Y = aX + b, сразу скажем, что 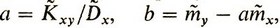 где
где 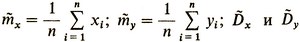 - дисперсии величин X и Y.
- дисперсии величин X и Y.
В нашем примере mx ≈ (19)70 (первые две цифры года опускаем), 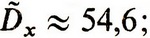 математическое ожидание взятой высоты
математическое ожидание взятой высоты 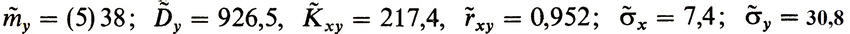 Таким образом, a ≈ 3,987; b ≈ - 242. Следовательно, уравнение прямой имеет вид y = 3,981x - 242.
Таким образом, a ≈ 3,987; b ≈ - 242. Следовательно, уравнение прямой имеет вид y = 3,981x - 242.
Расчет на 1985 год показывает, что y = 3,987*85 - 242 = 96,9, т. е. прогнозируемый на этот год результат 5 + 0,97 = 5 м 97 см. При х = 90 (т. е. в 1990 г.) из этого уравнения находим y = 108, следовательно, ожидаемый результат в 1990 г. около 6 м 08 см = 5 м + 1,08 м. Поживем - увидим!*.
* (На международных соревнованиях в Лос-Анджелесе в феврале 1984 г. спортсмен из Донецка Сергей Бубка с первой попытки преодолел планку на высоте 583 см, 4 марта француз Тьери Виньерон взял высоту 585 см. Наконец 1 сентября 1984 г. на международных соревнованиях "Гольден гала" в Риме Бубка покорил высоту 594 см, а 13 июля 1985 г. на международных соревнованиях в Париже он взял высоту 600 см. )
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'