5.2. Быстрее!

Обсудим задачу прогнозирования результата спортсмена на соревнованиях при помощи результатов, показанных им в процессе подготовки. Заметим, что любое предсказанное значение какого-либо параметра, вычисленное на основе ограниченного числа опытов, всегда, конечно, будет содержать элемент случайности, поэтому это значение называют оценкой соответствующего параметра.

Так, оценку времени t, которое показывает спринтер на стометровке, будем обозначать .

Рассмотрим сначала более общую задачу. Пусть имеется случайная величина X, закон распределения которой содержит неизвестный параметр t (обычно речь идет о математическом ожидании и дисперсии). Требуется найти подходящую оценку X значения этого параметра по результатам n независимых опытов, в каждом из которых случайная величина X принимает соответственно значения x₁, ..., x_n. Эти значения можно рассматривать как n "экземпляров" случайной величины X. Каждая из случайных величин X_t распределена по тому же закону, что и величина X. Вполне очевидно, что оценка является некоторой функцией величин x₁, ..., x_n и, следовательно, сама является случайной величиной.

Предъявим к оценке параметра t ряд требований, которым она должна удовлетворять, чтобы быть, в определенном смысле, "хорошей" оценкой. Во-первых, естественно потребовать, чтобы оценка при увеличении числа опытов приближалась (сходилась по вероятности) к значению параметра t. Оценка, обладающая таким свойством, называется состоятельной. Во-вторых, желательно, чтобы, пользуясь оценкой вместо t, мы не совершали систематической ошибки, т. е. чтобы для математического ожидания оценки выполнялось равенство M [] = t. Оценка, удовлетворяющая этому условию, называется несмещенной. Наконец, потребуем, чтобы выбранная оценка обладала по сравнению с другими наименьшей дисперсией; такая оценка называется эффективной. На практике не всегда удается удовлетворить всем этим требованиям одновременно. Например, может оказаться, что, хотя эффективная оценка и существует, формулы для ее вычисления оказываются слишком сложными, и приходится пользоваться другой оценкой, с несколько большей дисперсией.

В качестве оценки 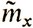математического ожидания m_x естественно выбрать среднее арифметическое полученных в опыте значений случайной величины X, т. е. 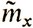= m^*_x = ¹/_n (x₁ + ... + x_n).

В курсе теории вероятностей показывают, что эта оценка состоятельная и несмещенная, а при некоторых предположениях о виде закона распределения случайной величины X эта оценка оказывается также и эффективной. В качестве оценки 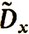дисперсии D_x выбирается величина

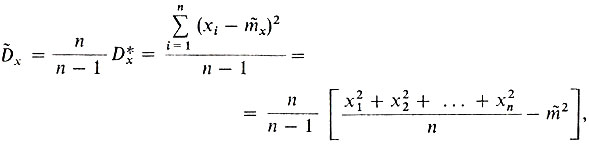
являющаяся ее состоятельной и несмещенной оценкой. Рассмотренная выше оценка параметра t (в частности, оценк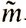и и 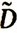математического ожидания и дисперсии) выражается одним числом и потому называется точечной. При незначительном объеме статистических данных, т. е. при малом числе n результатов независимых опытов, точечная оценка может существенно отличаться от оцениваемого параметра и приводить зачастую к значительным ошибкам. Поэтому при малых n пользуются так называемой интервальной оценкой. Интервальная оценка определяется двумя числами - концами оценивающего интервала.

Отсылая читателя за подробностями к руководствам по теории вероятностей, изложим лишь общие соображения, приводящие к понятию интервальной оценки. Допустим, что для параметра t уже получена несмещенная оценка . Ясно, что оценка тем точнее приближает параметр, чем меньше абсолютная величина разности |t - |. Коль скоро при некотором положительном числе е выполняется неравенство |t - |<ε, то ε естественно принять за меру точности оценки. Следует иметь в виду, однако, что методы математической статистики не позволяют утверждать, что для оценки ε неравенство |t - |<ε выполняется наверняка. Имеет смысл говорить лишь о вероятности P(|t - |<ε), с которой это неравенство выполняется.

Вероятность α = P(|t - |<ε), с которой осуществляется неравенство |t - |<ε, называется доверительной вероятностью {надежностью) оценки t с помощью числа .

Как правило, доверительную вероятность задают (назначают) заранее. Полагают, например, α равной 0,85, 0,90, 0,999 или иному числу, близкому к единице.

Итак, потребуем, чтобы при некотором неизвестном пока значении ε_α выполнялось требование P(|t - |<ε_α) = α. Это требование равносильно тому, что P( - ε_α<t<t + ε_α) = α. Последнее следует понимать в том смысле, что вероятность попадания точки t в интервал I_α = (t - ε_α; t + ε_α) равна α. Заметим, что сам интервал I_α также случаен, так как случайно положение на числовой оси его середины и случайна его длина 2ε_α, вычисляемая по опытным данным.

Интервал I_α называют доверительным интервалом, а его концы - доверительными границами. Доверительный интервал естественно рассматривать как диапазон возможных значений параметра г, совместимых с данными опыта (не противоречащих этим данным). В то же время вероятность выполнения неравенства |t - |>ε_α, т. е. вероятность того, что точка t не попадает в интервал I_α, составляет 1 - α, и чем ближе α к единице, тем эта вероятность ближе к нулю. Рамки настоящей книги не позволяют обосновать метод определения ε_α по назначенному α. Поэтому мы ограничимся "рецептурным" изложением.

В Допустим, по-прежнему, что проведено n независимых опытов над случайной величиной X и зафиксированы ее значения x₁, ..., x_n. Для неизвестных числовых характеристик величины X - математического ожидания и дисперсии - находим соответствующие оценки

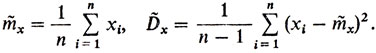
Можно доказать, что для назначенной вероятности α величина ε_α находится по формуле

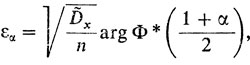
в которой 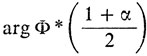является функцией, обратной функции Лапласа. Иными словами, 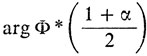является таким значением аргумента, при котором значение функции Лапласа равно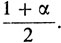

Для удобства дальнейших вычислений (в том числе и тех, на которые, быть может, решится читатель) приведем здесь небольшого объема табл. 1 значений функции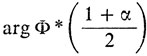

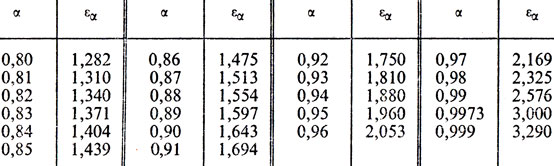
Таблица 1

Пусть наш спринтер в течение последнего месяца подготовки к соревнованиям 20 раз пробегал стометровку и показал следующие результаты: 10,5; 10,8; 11,2; 10,9; 10,4; 10,6; 10,9; 11,0; 10,3; 10,8; 10,6; 11,3; 10,5; 10,7; 10,8; 10,9; 10,8; 10,7; 10,9; 11,0. Требуется оценить ожидаемый на соревнованиях результат и найти доверительный интервал для доверительной вероятности α = 0,8.

Сначала находим статистические значения 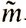= 10,78 и 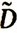= 0,064. Затем по таблице находим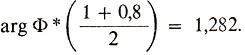

Таким образом,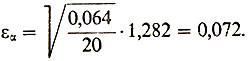

Границы доверительного интервала при этом оказываются равными 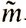- 0,072 = 10,71 и 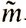+ 0,072 = 10,85.

Таким образом, с вероятностью 0,8 спортсмен покажет результат между 10,71 и 10,85. Если в качестве доверительной вероятности взять α = 0,9, то можно найти, что ε_α = 0,93 и соответственно с этой вероятностью ожидаемый результат спортсмена будет находиться между 10,52 и 11,06.