5.1. Случайные величины и их характеристики

Напомним необходимые для дальнейшего изложения понятия случайной величины и ее характеристик.

Будем называть случайной величиной такую величину, которая в результате опыта может принять то или иное значение, причем неизвестно заранее - какое именно.

Примером случайной величины может служить количество очков, выбитое на соревнованиях стрелком за 60 выстрелов. Заранее мы только знаем, какие значения может принимать эта величина, однако никак не можем знать, какое число очков будет выбито стрелком фактически. Другим примером может служить число, выпадающее при бросании игральной кости (кубика). Отметим, что случайные величины, принимающие только изолированные друг от друга значения из некоторого конечного или счетного множества, называют дискретными случайными величинами.

Понятие случайной величины играет важную роль в современной теории вероятностей. В дальнейшем случайные величины будем обозначать большими латинскими буквами, а ее возможные значения - малыми. Пусть случайная величина X может принимать значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Ясно, что p₁ + p₂ + ... + p_n = 1, так как в результате опыта величина X обязательно примет одно из возможных значений. Например, если X - число очков, выпавших при бросании игральной кости, то возможными значениями X будут x₁ = 1, x₂ = 2, ..., x₆ = 6, а все вероятности p_i (i = 1, ..., 6) равны 1/6. Составим следующую таблицу:

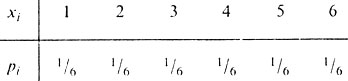
Такую таблицу, устанавливающую зависимость между возможными значениями случайной величины и соответствующими вероятностями, называют законом распределения случайной величины X; законом распределения случайной величины называют всякую функциональную зависимость между возможными значениями случайной величины и соответствующими им вероятностями. Указание этой функции полностью описывает случайную величину с вероятностной точки зрения. Однако весьма часто оказывается достаточным указать отдельные числовые параметры, характеризующие существенные черты распределения случайной величины. Такие числовые параметры называются ее числовыми характеристиками.

Введем некоторые, необходимые для дальнейшего обсуждения спортивных проблем числовые характеристики случайной величины.

Математическим ожиданием {средним значением) дискретной случайной величины X называют сумму произведений всех возможных ее значений x₁, ..., x_n на соответствующие вероятности этих значений p₁, ..., p_n, т. е.

где M[X] и m_x - обозначения математического ожидания случайной величины X.

Можно подсчитать, что в примере с кубиком M[X] = 3,5. Очевидно, что реально никогда не может выпасть такое количество очков, однако это среднее возможное число выпавших очков.

Дисперсией (рассеиванием) дискретной случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания. Дисперсия определяет степень разброса (отклонения) возможных значений случайной величины относительно ее математического ожидания. Дисперсия обозначается символами D [X] или D_x и вычисляется согласно определению по формуле

В рассмотренном примере с кубиком D_x = 8,75/3 ≈ 2,92.

Очень часто используют другую числовую характеристику:

среднее квадратическое отклонение σ_x = √D_x. В примере с кубиком σ_x = 1,71.

К сожалению,- вероятности возможных значений случайной величины, как правило, до проведения опытов неизвестны. Пример с игральным кубиком - приятное исключение. В то же время для обработки статистических данных необходимо знать числовые характеристики (математическое ожидание, дисперсию и некоторые другие) случайной величины. Как же поступить в тех случаях, когда нет никаких дополнительных соображений (например, из условий симметрии), позволяющих заранее заключить, чему равны вероятности p₁? В этих случаях ответ может дать только серия опытов. Разъясним существо дела.

Предположим, что проведена серия из N независимых испытаний (опытов), в которых каждое из возможных значений x_i случайной величины X появилось m_i раз (i = 1, ..., n). Составим среднее арифметическое m_x наблюдавшихся в опытах значений X:

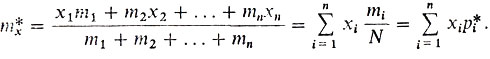
Величины p^*_i = ^m_i/N (i = 1, ..., n) называют частотой (статической вероятностью) появления значения x_i величины X в серии из N испытаний. Мы уже отмечали (см. с. 29), что при увеличении числа N испытаний частота p^*_i все меньше отличается от вероятности p_i. Поэтому и среднее арифметическое m^*_x наблюдавшихся значений случайной величины X все меньше будет отличаться от математического ожидания m_x, или, как говорят, m^*_x сходится по вероятности к m_x. Величину m^*_x называют статистическим математическим ожиданием.

Установленная связь между средним арифметическим и математическим ожиданием является также одним из проявлений уже упоминавшегося закона больших чисел Бернулли.

Во многих вопросах важную роль играет так называемая центрированная случайная величина = X - m_x, задающая отклонение X от своего математического ожидания m_x.

Если значения x₁, ..., x_n случайной величины X изобразить соответствующими точками числовой оси, то центрирование величины X (т. е. переход от X к ) означает перенос начала ординат в точку с абсциссой m_x.

Очевидно, что математическое ожидание центрированной случайной величины равно нулю:

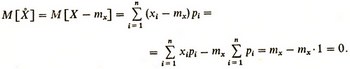
Вспомнив определение, отметим, что дисперсией D_x случайной величины X служит математическое ожидание квадрата центрированной случайной величины :

D_x = M[(X - m_x)²] = M[²].

Если в этом выражении математическое ожидание m_x заменить средним статистическим m_x^*, то придем к величине

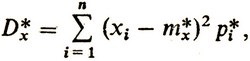
называемой статистической дисперсией случайной величины X.

Путем обработки результатов эксперимента удается получить статистические значения m_x^* и D_x^* математического ожидания и дисперсии.