6. Линейное программирование в спортивных задачах

6.1. Расстановка игроков в баскетбольной команде

Опытный тренер, хорошо знающий своих игроков, обычно успешно справляется с проблемой распределения между ними игровых обязанностей. Задача, связанная с использованием запасных игроков в разных сочетаниях, оказывается более сложной, если команда имеет "длинную скамейку" (в команде много игроков примерно одного класса). В этой ситуации даже опытному тренеру может помочь рассмотрение соответствующей математической модели.

Для начала ограничимся рассмотрением достаточно простой и не столь уже редкой ситуации. Незадолго до ответственной встречи в команде были заменены не только ряд игроков, но также и тренер. Его место занял новый, недостаточно опытный наставник, к тому же мало знакомый с отдельными игроками и с их возможностями. Перед новым тренером стоит задача: распределить между игроками команды обязанности таким способом, чтобы общая результативность действий всей команды оказалась наибольшей.

Попытаемся помочь новому тренеру, используя методы исследования операций. С этой целью придадим задаче, сформулированной на вербальном уровне, более точную форму и займемся построением ее математической модели. Если ничего не знать об игроках, то нечего и решать,- можно действовать наугад. Поэтому полезны даже ограниченные сведения. Следует воспользоваться каким-либо приемом, позволяющим в приемлемые сроки познакомиться с возможностями всех игроков. Обычно поступают следующим образом. Членам команды предлагают серию тестов, позволяющих оценить их способности играть центровым, защитником, разводящим, на левом и правом краях. Действия игроков, назовем их A, B, C, D, E, оцениваются в некоторых условных баллах.

Умудренные опытом тренеры могут сказать: к чему все это, ведь каждый игрок имеет свое амплуа, и нечего ставить, скажем, центрового на левый край или разводящего на роль защитника. В определенной мере это так, но при наличии значительного числа запасных игроков проблема формирования команды, выставляемой на встречу, приобретает особую сложность. Решается она таким же методом, как поставленная выше упрощенная задача.

В рамках этого же метода тренер может решать и такой вопрос: выпускать ли ему двух центровых или двух защитников (вместо одного).

Сведем результаты тестирования (в баллах) в табл. 6. Чем выше балл, тем предпочтительнее назначение игрока на соответствующее амплуа. Так, например, игрок В, вероятно, будет хорошим центровым и защитником, но слабым левым крайним, а игрок D, в общем-то, равно играет всюду, а центровым достаточно плохо.

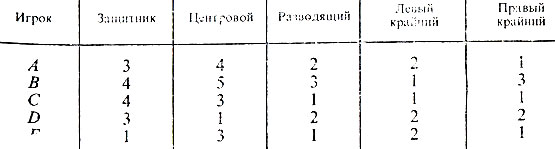
Таблица 6

Запомним смысл записанных в табл. 6 чисел и будем работать с матрицей баллов Г:

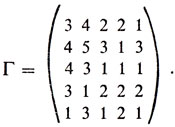
Вместе с тренером мы примем естественное предположение (критерий эффективности), согласно которому эффективность игры всей команды определяется суммой баллов, оценивающих игру каждого. Подобное предположение можно оспаривать и настаивать на ином критерии эффективности. Читатель вправе это сделать и предложить лучший вариант. Почти несомненно, что он окажется более сложным по своему строению. Выбранный нами критерий обладает огромным достоинством - он линейно зависит от баллов каждого игрока. Смысл этих слов станет ясным из последующего. Пока же рассмотрим одно из конкретных (малообдуманных) предложений: игрока A поставить защитником, B - в центр, C - разводящим, D - левым, E - правым крайним. При такой расстановке P эффективность (обозначим ее через Ф(P)) игры всей команды в баллах составит

Расстановке P отвечает табл. (матрица) 7. Она называется матрицей назначений, соответствующей расстановке P. Будем обозначать ее той же буквой P.

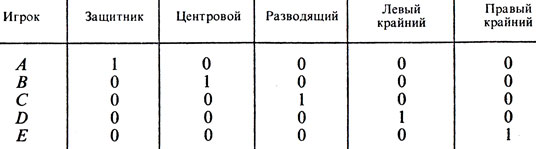
Таблица 7

Смысл этой таблицы очевиден: единица на пересечении строки игрока Л и столбца "Защитник" означает, что именно на эту роль А назначен; нуль подтверждает, что соответствующая роль ему не отводится. Легко усмотреть, что в каждой строке и каждом столбце матрицы назначений имеется в точности по одной единице, тогда как остальные элементы - нули. Подобное строение матрицы является отражением непреложного требования: каждый игрок назначается точно на одно амплуа и на каждое амплуа назначается в точности один игрок. Всех возможных матриц назначения, т. е. всевозможных способов расстановки игроков в команде, столько, сколько существует различных перестановок из пяти элементов, а именно, 5! = 1*2*3*4*5 = 120. Среди этих матриц необходимо выбрать такую матрицу P^* (их может оказаться и несколько), которая определит расстановку с наибольшим значением эффективности по сравнению с другими матрицами назначений P. Запишем это требование в виде Ф(P^*) = max_P Ф(P).

Число 120 возможных вариантов не так уж велико, и, потрудившись перебрать, тренер нашел матрицу назначений

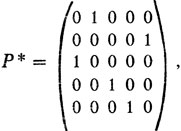
которой соответствует наибольшая перспективность игры команды Ф(P*) = 4 + 3 + 4 + 2 + 2 = 15. При такой расстановке A играет центровым, B - правым крайним, C - защитником, D - разводящим, E - левым крайним.

Впрочем, это решение оказалось не единственным оптимальным. Помощник тренера обнаружил, что то же наибольшее значение эффективности возникает при расстановке согласно матрице назначений

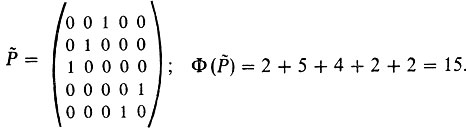
Итак, тренер решил задачу, как говорят, "прямым перебором" возможных вариантов. Это удалось осуществить благодаря незначительному числу вариантов (малой размерности задачи). Положение резко изменится к худшему, если в распоряжении тренера имеются запасные игроки, которые к тому же (как и основные) с различными партнерами играют с различной результативностью. И тут возникает соблазн учесть в нашем исследовании и этот момент. В действительности такой учет возможен, но приведет к усложнению модели, неоправданному на данном этапе. Ограничим себя и будем считать, что результаты тестирования дают некоторые средние баллы, с учетом игры с разными партнерами. Даже при наличии по одному запасному игроку на каждое место в команде, т. е. при общем числе игроков, равном 10, соответствующая задача о назначениях требует перебора, вообще говоря, 10! = 3628800 ≈ 3,6*10⁶ вариантов. Осуществление прямого перебора в этом случае немыслимо; можно лишь воспользоваться ЭВМ. Оценим затраты времени. В году 3*10⁷ секунд. При затрате на один перебор лишь одной секунды потребуется 1/10 года, при затрате одной миллисекунды - 1/10⁴ года, при затрате одной микросекунды - 1/107 года, т. е. 3 секунды. Но перебор 20! (это больше, чем 10¹⁰*10!) вариантов займет уже 3000 лет! Оценки - малоутешительные. К счастью, однако, для задачи о назначениях (она называется также задачей выбора) существует удобная для решения математическая модель. Модель формализуется в терминах линейного программирования - самого завершенного и нашедшего наиболее широкое, применение раздела математического программирования или теории исследования операций.

Построим математическую модель задачи о назначениях. Удобства ради припишем игрокам A, B, c, D, E, соответственно номера i = 1, 2, 3, 4, 5. Аналогично обозначим номерами j = 1, 2, 3, 4, 5 обязанности защитника, центрового, разводящего, левого и правого крайних соответственно. Затем введем в рассмотрение 25 неизвестных xy (i = 1, ..., 5, j = 1, ..., 5), значения которых мы станем интерпретировать как указания о назначении игрока под номером i на выполнение обязанностей типа j. При этом каждая из переменных x_ij может принимать лишь одно из двух возможных значений:

Совокупность пока неизвестных величин x_ij составляет матрицу назначений

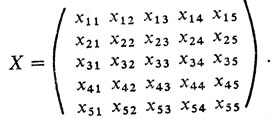
Численные реализации таких матриц нам уже встречались в разобранном ранее примере. Уже известно, что в каждой строке и каждом столбце матрицы X лишь единственный из элементов равен 1, остальные равны нулю. Это обязательное условие (ограничение) может быть записано в соответствующей форме: сумма всех элементов по каждой строке (столбцу) равна 1:

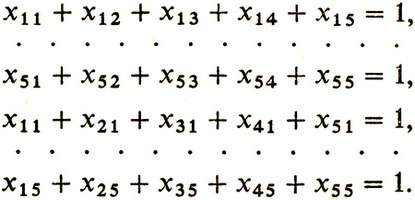
В более экономной записи системы ограничений примут вид

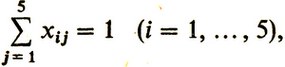(1)

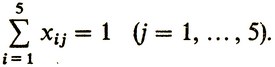(2)

К этому следует присоединить требование неотрицательности неизвестных

Игрок под номером i, назначенный на амплуа j, внесет свою долю в общую эффективность Ф(X) в размере a_ijx_ij Здесь a_ij - элемент соответствующей матрицы баллов Г, расположенный на пересечении ее i-й строки и j-го столбца. Общая эффективность игры команды составит сумму из 25 слагаемых

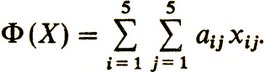(4)

В нашем конкретном примере (см. табл. 6)

Поиск матрицы назначений X, доставляющей эффективности Ф(X) наибольшее значение, сводится к следующей математической задаче: среди всех неотрицательных решений

системы ограничений (1) и (2) выбрать такое, которое придает Функции (4) наибольшее значение (оптимизирует Ф(X)).

Сформулированная задача и есть математическая модель задачи о распределении обязанностей в баскетбольной команде (при отсутствии запасных игроков).

Допустим, что игроков в команде n>5. Тогда введем дополнительно к известным пяти еще k = n - 5 фиктивных амплуа (мест в команде), считая, что на каждом из них тестовый балл a_ij (i = 1, ..., n; j = 6, 7, ..., n) каждого из игроков равен нулю. После такого шага приходим к известной уже задаче о выборе при равном числе претендентов и мест в команде. Возникает математическая модель, отличающаяся от (1) - (4) только числом переменных x_ij и числом ограничений.

Аналогичным путем могут быть сформулированы и просчитаны различные варианты задач, в которых, например, некоторые места сохраняются за основным составом, остальные - распределяются между запасными.

Решение общей задачи о назначениях может быть осуществлено универсальным симплекс-методом (см. с. 122). Более предпочтительным, однако, оказывается специализированный, так называемый "венгерский метод", предложенный Эгервари (1931 г.), удачно использующий специфику ограничений задачи. Описание этого метода читатель сможет найти, например, в книгах [17, 18].