4.3. О недостатках принципа большинства

Одним из самых известных и, по-видимому, самых древних принципов выбора результирующего отношения является принцип большинства. Принцип этот состоит в следующем. Пусть выданы N ранжировок m объектов: r₁, ..., r_N. В этом случае на первое место в результирующей ранжировке попадает объект, который большинство экспертов поставили на первое место; на второе - объект, который большинство поставили на второе и т. д.

Пусть, например, выданы три ранжировки четырех объектов:

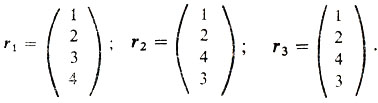
В результирующей ранжировке объекты получат следующие ранги:

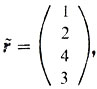
ибо большинство первое место отвело первому объекту, второе место - второму, третье - четвертому и четвертое - третьему.

Однако в еще более ранних исследованиях по проблеме выбора наилучшей ранжировки (объектов), которые принадлежат французским ученым Жану Антуану Кондорсе (1743 -1794) и Жану Шарлю Борда (1733-1799)^*, указано на недостаточность процедуры определения результирующего отношения по принципу большинства.

^* (Математик и философ Жан А. Кондорсе - автор трактата "Эскиз исторической картины прогресса человеческого разума", в котором он предсказал возможность существенного продления жизни человека.)

Приведем пример ([15]), иллюстрирующий точку зрения Кондорсе. Допустим, что рассматриваются двадцать объектов (альтернатив) a_i (i = 1, ..., 20) и их ранжировки, высказанные десятью экспертами:

Здесь для большей наглядности альтернативы a₁ размещены соответственно занятым в каждой ранжировке местам. По правилу большинства в этом примере наилучшей должна быть признана альтернатива a₂, хотя очевидно, что с большим успехом она может быть признана наихудшей альтернативой.

Иногда при использовании правила большинства вводят дополнительные требования, позволяющие устранить указанный недостаток, В частности, наилучшей может быть объявлена альтернатива, которую считают наилучшей не менее половины экспертов. Между тем в реальных экспертизах такая ситуация случается не очень часто. Кондорсе был предложен следующий принцип выбора наилучшей ранжировки. На основании полученных от экспертов ранжировок для каждой пары альтернатив a_i, a_j вычисляется величина S_ij - число экспертов, считающих, что a_i лучше a_j. Находится, соответственно, и величина S_ij. Если S_ij>S_ji, то альтернатива a_i считается более предпочтительной, чем a_j (символически факт "a_i предпочтительней, чем a_j" записывается так: a_i> a_j). Альтернатива a_i объявляется наилучшей альтернативой - альтернативой Кондорсе - если S_ij>S_ji для всех j≠i В рассмотренном выше примере такой альтернативой является a₁.

Однако при использовании принципа выбора Кондорсе может возникать указанный им же парадокс, являющийся следствием нетранзитивности коллективных предпочтений. Под нетранзитивностью понимается нарушение свойства транзитивности, т. е. следующий факт: при a₁>a₂ и a₂>a₃ все же a₃>a₁.

Проиллюстрируем парадокс Кондорсе на примере. Допустим, что три эксперта проранжировали три альтернативы следующим образом:

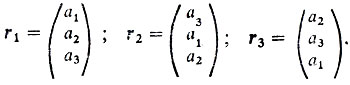
В этом случае S₁₂>S₂₁, S₂₃>S₃₂, но S₁₃<S₃₁, следовательно, a₁>a₂, a₂>a₃, но a₃<a₁, и потому альтернативы Кондорсе в этом случае не существует.

Заметим, что число экспертиз, приводящих к парадоксу Кондорсе, в среднем немного меньше 1/10 общего числа экспертиз при их фиксированном числе. В реальных задачах, когда мнения экспертов могут сильно отличаться друг от друга, вероятность возникновения этого парадокса даже выше 1/10.

Другой способ усовершенствования принципа большинства был предложен Борда и состоит в следующем. Объектам, проранжированным экспертом, приписывают "веса": последнему - вес, равный нулю, предпоследнему - единице и т. д.

Если через s_i обозначить сумму весов, приписанных альтернативе a_i всеми экспертами, то результирующим объявляется отношение 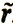= (a_i1, a_i2, ..., a_in), для которого s_i1≥s_i2≥ ... ≥ s_in. Способ Борда также не лишен недостатков. Например, альтернатива Кондорсе, т. е. лучшая любой другой при парном сравнении, может оказаться не выбранной в качестве наилучшей по принципу Борда.

Рассмотрим простой пример. Допустим, что пять экспертов проранжировали объекты a₁, a₂, ..., a₅ следующим образом:

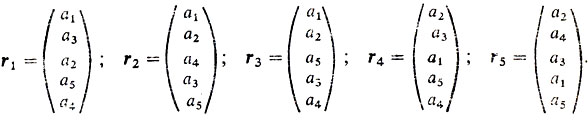
Лучшим по принципу парных сравнений Кондорсе является объект a₁ (проверьте сами!). Однако по принципу Борда он будет хуже a₂, так как s₁ = 15, a s₂ = 16.

Указанных в этом разделе недостатков лишен принцип выбора, предложенный Кемени. Как уже отмечено, этот принцип основан на выборе среднего отношения (ранжирования), наименее удаленного от высказанных экспертами. Ниже будут предложены разработанные авторами методы отыскания среднего при судействе фигурного катания.