
4.2. Ранжировки
Предположим, что п заданных объектов должны быть оценены N экспертами. Каждый эксперт обязан сообщить отношение. в виде вектора рангов, т. е. указать, какой из оцениваемых объектов имеет по его мнению ранг, равный единице, какой ранг - равный двум и т. д. Такое отношение, как уже отмечалось выше, называют ранжировкой. Нетрудно убедиться, что число различных возможных ранжировок равно n!. Обозначим множество всех возможных ранжировок через R. Ранжировку, сообщаемую i-м экспертом, будем обозначать буквой ri = (ri1, ri2, ..., rin), где rim - ранг (место) m-го объекта (m = 1, ..., n), указанный i-м экспертом.
Пусть, например, двое судей после выступления четырех спортсменов А, В, С, D должны указать в итоговом протоколе их расстановку по местам. Предположим, что судьи выдали ранжировки r1 = (3, 1, 2, 4) и r2 = (2, 1, 3, 4). Это означает, что первый судья отвел первое место спортсмену В, второе - спортсмену С, третье - А и четвертое место - D. В то же время второй судья присудил первое место спортсмену В, второе - А, третье - С, четвертое - D. Значит, в принятых нами обозначениях r11 = 3, r12 = 1, r13 = 2, r14 = 4, r21 = 2, r22 = 1, r23 = 3, r24 = 4.
Прежде чем показать, каким образом выбирается средняя оценка, введем понятие расстояния (метрики) d(ri, rj) между ранжировками. Естественно потребовать, чтобы, подобно обычному расстоянию, расстояние между ранжировками удовлетворяло следующим требованиям (вспомним элементарную геометрию!).
- Расстояние между ранжировками не может быть отрицательным: d(ri, rj) ≥ 0; расстояние равно нулю тогда и только тогда, когда ранжировки тождественно равны: d(ri, rj) = 0 влечет за собой ri = rj и обратно.
- Расстояние симметрично: d(ri rj) = d(rj, ri).
- Расстояние подчиняется неравенству треугольника: d(ri, rj)≤d(ri, rk) + d(rk, rj). Учитывая нужды экспертизы, к этим трем аксиомам были присоединены еще следующие:
- Пусть ранжировки r'i и r'j получены соответственно из ранжировок ri и rj в результате некоторого переобозначения объектов; тогда
d(ri', r'j) = d(ri, rj).
- Минимальное положительное расстояние между ранжировками равно 1.
- Если ранжировка rk лежит между ранжировками ri и rj, то
d(ri, rj) = d(ri, rk) + d(rk, rj).
Можно доказать (см. [15; 29]), что существует единственная метрика, удовлетворяющая всем шести требованиям. При этом расстояние между ранжировками ri и rj определяется по формуле
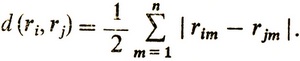
В нашем примере со спортсменами А, В, С и D и двумя судьями расстояние между ранжировками судей составляет
d(r1, r2) = 1/2[|3-2| + |1-1| + |2-3| + |4-4|] = 1.
Очень часто в качестве среднего при наличии нескольких ранжировок r1, ..., rN выбирают такую ранжировку 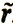 , сумма расстояний от которой до исходных есть величина наименьшая из всех возможных. Такая ранжировка r называется медианой Кемени. Медиана Кемени
, сумма расстояний от которой до исходных есть величина наименьшая из всех возможных. Такая ранжировка r называется медианой Кемени. Медиана Кемени 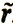 находится из решения задачи минимизации по всем ранжировкам r из множества R суммы расстояний от r до r1, ..., rN, т. е. определяется формулой:
находится из решения задачи минимизации по всем ранжировкам r из множества R суммы расстояний от r до r1, ..., rN, т. е. определяется формулой:
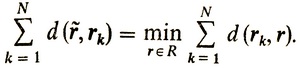
В общем случае решение такой задачи является весьма сложным, и мы не имеем возможности задерживаться на этом вопросе (см. [15]).
Сейчас мы рассмотрим различные принципы выбора результирующего отношения в случае ранжирования объектов с ретроспективой развития этих принципов.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'