3.13. Модель тай-брейка (завершим тай-брейк!)

Таким образом, вне зависимости от того, чем закончился розыгрыш первого мяча, вероятности выигрышей следующих мячей очень быстро стабилизируются: начиная с третьего-четвертого мяча они уже почти не отличаются. Вот почему после возникновения в тай-брейке счета "по шести" при дальнейшем рассмотрении игры (до достижения одной из сторон превосходства в два мяча) можно считать вероятности выигрыша АВТОРОМ и ЧИТАТЕЛЕМ очередного мяча постоянными и равными, соответственно, ⁷/₁₂ и ⁵/₁₂.

Граф возможных изменений счета разыгранных мячей в тай-брейке таков же, как и при изменении счета геймов в сете (рис. 5). Отличие лишь в числовых значениях вероятностей перехода из рассматриваемого состояния в другое возможное.

Используя граф, изображенный на рис. 5, можно подсчитать (аналогично тому, как это сделано при розыгрыше гейма - см. с. 34) распределение p⁰ = (p⁰₁, p⁰₂, ..., p⁰₅) вероятностей достижения после розыгрыша одиннадцати или двенадцати мячей каждого из пяти состояний: "тай-брейк АВТОРА", "больше АВТОРА", "ровно", "меньше АВТОРА" (или "больше ЧИТАТЕЛЯ"), "тай-брейк ЧИТАТЕЛЯ". Граф марковской цепи с этими пятью состояниями изображен на рис. 9.

Рис. 9

Распределение p⁰ примем в качестве начального для периода случайного блуждания. Введем переходную матрицу рассматриваемой цепи:

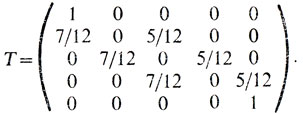
Тогда распределение вероятностей p¹ достижения упомянутых пяти состояний после розыгрыша следующего мяча найдется как произведение вектора p⁰ на матрицу T:p¹ = p⁰T. Распределение вероятностей после очередного мяча составит p² = p¹T и т. д., пока не стабилизируются значения координат вектора pⁿ = p^(n-1)T распределения вероятностей.

Рассмотренную ситуацию можно несколько усложнить, предположив, что и противник АВТОРА (ЧИТАТЕЛЬ) также усиливает свои игру, внимание, собранность после проигранного мяча, и принять, что вероятность выигрыша им следующего мяча составит не 0,5, а, например, 0,6. В таком случае матрица переходов примет вид

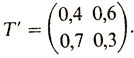
Таким образом можно в некоторой степени учитывать

(психологические, эмоциональные и им подобные факторы. Для этой усложненной ситуации читатель может самостоятельно подсчитать предельные вероятности p^* и q^*, с которыми обе стороны придут к завершающей фазе тай-брейка.