
3.12. Играя - обучайся!
В процессе игры каждый теннисист учитывает свои ошибки технического и тактического характера, приспосабливается к манере, темпу, стилю игры противника, короче говоря, обучается и совершенствует свою игру.
Это обстоятельство может быть учтено в модели, построенной в терминах уже известного читателю математического аппарата - цепей Маркова. Можно, в частности, считать, что в марковских цепях, описывающих розыгрыш гейма (сета), вероятности переходов из одного состояния в последующее меняются по тем или иным законам.
Начнем с рассмотрения ситуации, которая возникает при розыгрыше мячей в тай-брейке.
Предположим, что игрок (АВТОР) после выигранного мяча (состояние S1) следующий мяч выигрывает с вероятностью p = 0,5 (его внимание и усердие находятся в норме - они обычные). Но вот после проигранного мяча (состояние S2) АВТОР более собран, более внимателен, проявляет большее усердие. Поэтому естественно считать, что следующий мяч он выиграет с большей вероятностью, например, с вероятностью q = 0,7. Тем самым возникает следующая матрица переходов из состояния Si в Sj (i,j = 1, 2):
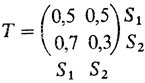
и соответствующий ей граф состояний (рис. 8).
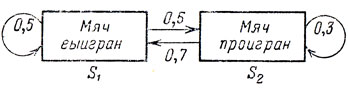
Рис. 8
При розыгрыше первого мяча по системе тай-брейк подает тот теннисист, чья очередь подавать при счете 6:6. Его соперник подает при розыгрыше второго и третьего мячей. В последующем каждый теннисист подает поочередно при розыгрыше двух следующих мячей, пока не будет завершен гейм (а с ним и сет). Предположим, что АВТОР начал тай-брейк с выигранного мяча. Вероятность выигрыша им второго мяча в нашем примере составит p1 = 0,5, вероятность проигрыша q1 = 0,5. Будем считать (p1, q1) начальным распределением вероятностей. Каковы вероятности того, что следующий, третий мяч им будет выигран и соответственно проигран?
Обозначим соответствующие вероятности через p2 и q2 и найдем: p2 = 0,52 + 0,5*0,7 = 0,60, q2 = 0,52 + 0,5*0,3 = 0,40. Другими словами, распределение (p2, q2) вероятностей исхода розыгрыша третьего мяча дается произведением начального распределения (p1, q1) на матрицу T:
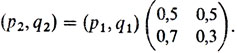
Повторяя эти рассуждения, найдем, что распределение вероятностей исхода розыгрыша (n + 1)-го мяча составит
(pn, qn) = (pn-1, qn-1)T = (p1, q1)Tn-1.
Так, в частности, p3 = p2*0,5 + q2*0,7 = 0,580, q3 = p2*0,5 + q2*0,3 = 0,420; p4 = 0,584; p5 = 0,5832; p6 = 0,58336; q4 = 0,416; q5 = 0,4168; q6 = 0,41663 и т. д. Наконец, можно установить значения предельных вероятностей:
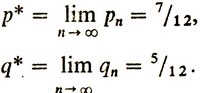
Предположим теперь, что АВТОР начал тай-брейк с проигранного мяча. В этом случае начальным распределением будет p'1 = 0,7, q'1 = 0,3, а распределение результатов розыгрыша третьего мяча составит
p'2 = 0,7*0,5 + 0,3*0,7 = 0,56,
q'2 = 0,7*0,5 + 0,3*0,3 = 0,44.
Для (n + 1)-го мяча получим распределение
(p'n, q'n) = (p'n-1, q'n-1)T = (p'1, q'1)Tn-1.
Так, в частности,
p'3 = 0,588; p'4 = 0,5824; p'5 = 0,58352;
q'3 = 0,412; g'4 = 0,4176; q'5 = 0,41648;
p'6 = 0,583296; q'6 = 0,416704.
Предельные вероятности принимают прежние значения
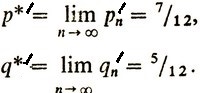
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'