3.14. Марковские процессы - с дошкольных лет

Как это ни парадоксально звучит, но с марковскими процессами мы знакомы еще с дошкольного возраста. Каждому известна детская игра, в которой фишки участников должны переместиться из начального пункта A₀ ("старт") в конечный A_k ("финиш"). Попав в тот или иной промежуточный пункт A_j, фишка может либо приблизиться к финишу (за счет "льготы", предусмотренной условиями

"игры), либо удалиться от него (за счет "штрафа"). Число шагов, на которое фишка перемещается из занимаемого ею пункта A_i в пункт A_j, определяется числом очков, выпавшим на брошенной игральной кости. Поэтому вероятность того, что фишка из пункта A_i переместится в A_j, не зависит от того, каким путем фишка оказалась в позиции A_i,а определяется лишь вероятностью p_ij выпадения соответствующего числа очков на грани кости. Возникает ситуация, в точности характерная для марковского процесса с дискретным (конечным) множеством состояний A₀, A₁,..., A_i,.., A_j,..., A_k и дискретным временем. Счет моментов переходов из одного состояния в другое заменяется счетом числа самих переходов. Позиции A_i (i = 0, ..., k) ассоциируются с состояниями системы S игры. Тогда карту игры с изображенными на ней позициями и вероятностями переходов из каждой позиции в последующие можно считать графом соответствующей цепи. Граф этот, как правило, куда сложнее изменения счета в гейме или сете.

В студенческую пору и в зрелом возрасте те, кому привелось заниматься стохастическими задачами исследований операций, вновь обращаются к случайным процессам, развитие и исход которых зависят от ряда случайных факторов. Важную роль во многих задачах играют так называемые марковские случайные процессы.

В таких процессах "будущее зависит от прошлого только через настоящее". Или иначе: случайный процесс называют марковским, если при любом его состоянии S₀ вероятностные характеристики процесса в последующем зависят только от настоящего состояния S₀ и не зависят от того, когда и каким образом система пришла в это состояние.

Уточним данное определение. Рассмотрим некоторую систему S, которая в любой момент времени может находиться только в одном из n несовместных состояний S₁,..., S_n. В нашем примере - это состояния счета в процессе игры в теннис. Пусть состояние системы меняется в зависимости от некоторого параметра t, причем переход из состояния в состояние зависит от вмешательства случая. Параметр t можно условно назвать временем и считать, что он изменяется либо непрерывно, либо принимает некоторую последовательность t₁, t₂, ..., t_n значений (в нашем примере - это моменты завершения розыгрыша очередного мяча).

Процесс, описывающий поведение такой системы, называют конечной цепью Маркова при выполнении следующего условия: если в данный момент времени τ система находится в состоянии S_i, то в следующий момент i>τ система будет находиться в состоянии S_j с некоторой вероятностью P_ij(τ, t), которая не зависит от поведения системы до момента τ.

Таким образом, конечная цепь Маркова - это случайный процесс, протекающий на конечном множестве состояний некоторой системы, для которого вероятность системы попасть в то или иное состояние зависит только от состояния, предшествующего данному. Вероятности P_ij(τ, t) называются переходными вероятностями. Марковская цепь называется однородной, если переходные вероятности зависят только от разности t - τ, т. е. если P_ij(τ, t) = P_ij(τ - t).

Если принять τ = 0 и в процессах с дискретным временем моменты t₁, ..., t_n, ... отождествить с индексами 1, 2, ..., и, ..., то можно упростить обозначения: P_ij (τ, t_k) = P_ij(0,k) = P_ij(k) и P_ij(t_i, t_k) = p_ij(k - l). В частности, для любых соседних моментов времени l и l + 1 имеем P_ij(t₁, t_l+1) = P_ij(1). Эти величины и есть вероятности перехода из любого состояния S_i в другое S_j (включая вероятность P_ii(1) задержки в состоянии S_i) за один шаг. Переходные вероятности P_ij(1) = P_ij образуют матрицу переходов конечной марковской цепи:

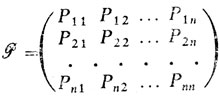
В каждой i-й строке матрицы находятся вероятности переходов из одного и того же состояния S_i в любое возможное S_j. Естественно, что сумма переходных вероятностей в каждой строке равна единице:

Примером такой матрицы может служить матрица T переходных вероятностей для периода случайного блуждания при завершении гейма (см. с. 35). Зная матрицу переходов 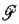, можно подсчитать вероятности переходов системы из состояния S_i в состояние S_j за n шагов. Так, в частности, переходные вероятности P_ij(2) за два шага составляют матрицу 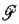₂, которая получается возведением в квадрат матрицы 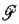: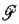₂ = 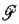². Переходные вероятности P_ij(n) за n шагов образуют матрицу, равную n-й степени 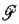: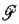_n = ⁿ. Именно так мы поступали, рассматривая завершающую фазу розыгрыша гейма, а также тай-брейка.

Итак, на примере моделирования игры в теннис мы познакомились со случайным марковским процессом с дискретными состояниями; переход из состояния в состояние в таких процессах происходит мгновенно. Если же система не скачком (мгновенно), а постепенно, с течением времени переходит из одного состояния в другое, то говорят о процессе с непрерывными состояниями. В том случае, когда переходы реализуются в заранее фиксированные моменты времени t₁, t₂, ..., t_n, ..., говорят о процессе с дискретным временем; при возможности переходов в случайные моменты времени - о процессах с непрерывным временем^*.

^* (В некоторых практических задачах случайные процессы в первом приближении могут считаться марковскими (хотя, строго говоря, ими не являются). В некоторых случаях, путем искусственного "брикетирования" всего "прошлого" и включения его в "настоящее" состояние S₀, удается поместить случайный процесс в рамки марковского. Однако такой прием приводит к значительному усложнению модели и затрудняет ее изучение.)

Работа всякого технического устройства, собранного из отдельных составляющих элементов, может быть описана в терминах марковского процесса с дискретным множеством состояний и непрерывным временем. Дело в том, что узлы устройства могут выходить из строя (а затем и восстанавливаться) в случайные моменты времени. При описании подобных процессов используют вероятности P_i(t) того, что в момент времени t система находится в состоянии S_i. Эти вероятности состояний находят как решения системы линейных дифференциальных уравнений (уравнений Колмогорова).

Некоторые из процессов могут протекать весьма длительно и при неограниченном возрастании времени t приобретать стационарный характер. В этом режиме вероятности состояний оказываются постоянными (не зависящими от времени) и называются финальными. Финальные вероятности находят уже из системы линейных алгебраических уравнений, в которые превращаются в этом случае дифференциальные. Обширное приложение марковские процессы нашли в теории массового обслуживания - одного из разделов теории исследования операций. Заинтересовавшегося читателя отсылаем к уже упомянутым монографиям [1; 25].