
3.10. Продолжим игру до сета
Итак, мы нашли вероятности выигрыша одного гейма каждой из сторон. Перейдем теперь к определению вероятностей выигрыша сета. С этой целью выпишем всевозможные изменения счета в пределах сета в виде соответствующего ориентированного графа (рис. 5).
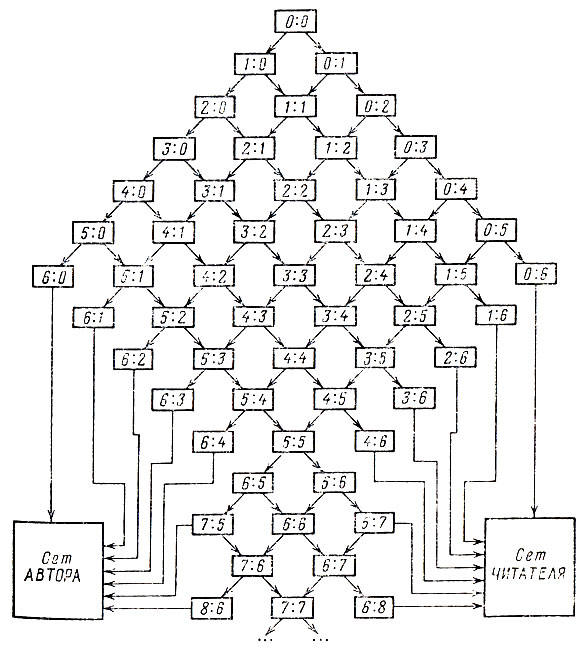
Рис. 5
Рассматривая вновь возникшую конечную марковскую цепь (рис. 5), видим, что после розыгрыша одиннадцати или двенадцати геймов возникает процесс случайного блуждания. Он определен требованием иметь для победы в сете преимущество не менее, чем на два гейма. Граф этого случайного блуждания представлен на рис. 6.

Рис. 6
Используя те же методы, что и при нахождении вероятностей выигрыша гейма, можно найти вероятности выигрыша сета:
P(сет АВТОРА) = 0,966, P(сет ЧИТАТЕЛЯ) = 0,034.
Как видим, вероятность выигрыша сета АВТОРОМ близка к единице. Этого, в общем, и следовало ожидать, ведь АВТОР выигрывает отдельный мяч с вероятностью в полтора раза большей, чем ЧИТАТЕЛЬ. Подсчет показывает (проверьте сами!), что матч из трех сетов АВТОР выигрывает с вероятностью 0,996, а из пяти - с вероятностью 0,9996, т. е. практически - наверняка. Ясно поэтому, что более трех сетов играть в этом случае нецелесообразно.
Но допустим теперь, что класс игроков практически одинаков, например, вероятность выигрыша мяча АВТОРОМ составляет 0,51, а ЧИТАТЕЛЕМ - 0,49. Иными словами, из ста разыгранных мячей ЧИТАТЕЛЬ выигрывает в среднем лишь на два меньше, чем АВТОР. В этом случае можно найти, что вероятность выигрыша сета АВТОРОМ составит 0,573, а ЧИТАТЕЛЕМ 0,427. Таким образом, при разнице вероятностей выигрыша мяча в 0,02 разница в вероятностях выигрыша сета возрастает в 7 раз. Тем не менее при розыгрыше одного сета преимущество сильной стороны оказывается не очень убедительным: из десяти встреч в среднем АВТОР выиграет шесть раз, ЧИТАТЕЛЬ - четыре.
Вероятность выигрыша каждой стороной по одному сету, т. е. вероятность счета 1:1, велика и составляет 0,488 (подсчитайте ее, используя граф на рис. 7).
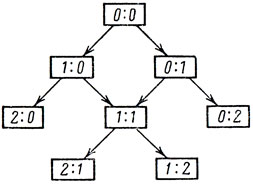
Рис. 7
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'