3.6. Модель игры - марковская цепь

Теперь перейдем к построению математической модели игры в теннис между АВТОРОМ (А) и ЧИТАТЕЛЕМ (Ч), предполагая известными вероятности Р(А) и Р(Ч) выигрыша мяча АВТОРОМ и ЧИТАТЕЛЕМ соответственно. Пусть для определенности Р(Ч) = 0,4; Р(А) = 0,6 (АВТОР играет несколько лучше ЧИТАТЕЛЯ). Не случайно, что Р(Ч) + Р (А) = 0,4 + 0,6 = 1 (проигрыш мяча одной стороной означает выигрыш его другой стороной). На рис. 3 показано, как последовательно может изменяться счет в гейме. Числа рядом со стрелками указывают, с какой вероятностью может произойти соответствующее изменение счета. Например, при счете 15:15 с вероятностью 0,6 мяч выиграет АВТОР, т. е. счет станет 30:15, а с вероятностью 0,4 мяч выиграет читатель, т. е. счет станет 15:30.

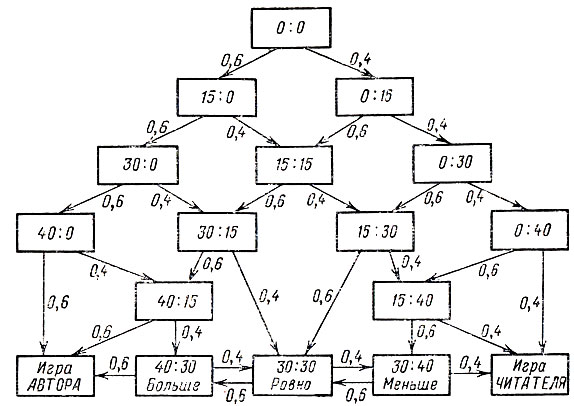
Рис. 3

Будем говорить, что мы имеем систему - игру в теннис. Состояния системы определяются счетом в пределах гейма. При этом переход из одного состояния (счета) в последующее зависит только от настоящего состояния и, конечно, от вероятности перехода (от чисел у стрелок), однако он не зависит от предшествующих состояний^*. Отметим, что любая система, в которой переход из одного состояния в другое не зависит от предыстории процесса, а зависит только от текущего состояния, называется в теории вероятностей марковской цепью или цепью Маркова (А. А. Марков, 1856 - 1922), В общем случае конечную марковскую цепь можно задать в виде геометрической схемы (так называемого ориентированного графа), где прямоугольники (вершины графа) изображают состояния, а соединяющие их стрелки (ребра графа) указывают на переходы из одного состояния в другое. Рядом с каждой стрелкой записана вероятность соответствующего перехода. Следовательно, рис. 3 дает нам конкретный пример графа конечной марковской цепи, описывающего состояния системы - игры в теннис в рамках гейма.

^* (Мы несколько идеализируем ситуацию, не учитывая некоторые иные обстоятельства, например, фактор подачи, психологические факторы, адаптацию к стилю игры партнера, т. е. процесс "обучения" в ходе игры.)

Отметим, что на рис. 3 по понятным причинам счет 40 : 30 объединен со счетом "больше", счет 30:30 - со счетом "ровно", а счет 30:40 - со счетом "меньше".

В марковской цепи могут существовать состояния различных типов [25]. Во-первых, невозвратное состояние, т. е. такое, выйдя из которого система вновь попасть в него не может. В нашем случае таких состояний довольно много, среди них, например, состояния 15:30 или 40:0 и т. п. Во-вторых, возвратное состояние - всякое состояние, не являющееся невозвратным. Такими у нас являются состояния «больше», «разно», «меньше». Следующий важный тип состояний - поглощающее. Состояние называется поглощающим, если, попадая в него, система и впредь остается в кем, не имея возможности перейти ни в какое иное состояние. В нашем примере таких состояний два: «игра АВТОРА» и «игра ЧИТАТЕЛЯ».