
Глава 7. Задачи без решения
Решение некоторых приведенных здесь задач известны, решения же других задач до сих пор еще не найдены. В этом разделе есть и легкие, и трудные задачи, однако решение какой-либо из них может свидетельствовать об умении самостоятельно мыслить.
Плюсы и минусы
Приведенная слева фигура состоит из 14 знаков "+" и из 14 знаков "-". Они расставлены таким образом, что под двумя одинаковыми знаками всегда стоит знак "+", а под двумя различными знаками - знак "-".
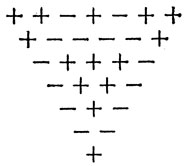
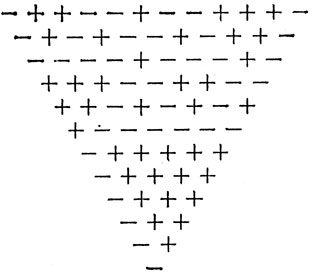
Если бы в первой строке было n знаков, то в аналогичной фигуре было бы всего 1/2n (n + 1) знаков (наш пример отвечает числу n, равному 7). Так как 1/2n есть четное число при n = 3, 4, 7, 8, 11, 12 и т. д., то можно спросить, возможно ли для любого из этих n построить фигуру, аналогичную нарисованной и начинающуюся с п знаков в самой верхней строке. В частности, мы спрашиваем о случае n = 12.
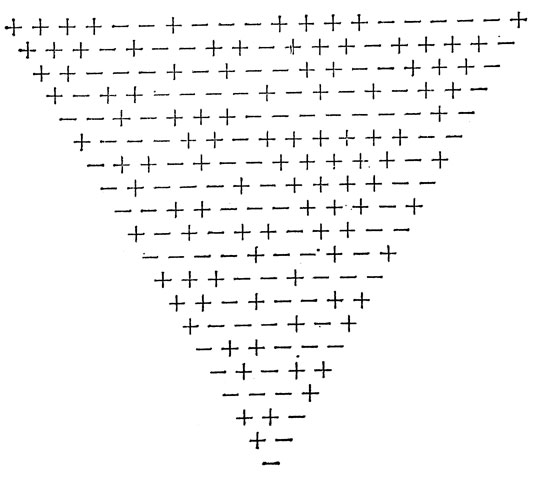
Общее решение до сих пор неизвестно. Приводим решения для n = 12 (рис. справа) и (на с. 42), из которых путем отбрасывания первой строки получаем также решения для n = 11 и n = 19.
Треугольник в треугольнике
Один треугольник имеет стороны а, b, с, а другой - стороны а', b', с'. Какие условия, связывающие числа а, b, с, а', b', с; необходимы и достаточны для того, чтобы первый треугольник можно было поместить внутри другого?
Части квадрата
Единичный квадрат разделен на 3 произвольные части. Пусть г - некоторое положительное число, меньшее √65/64.
Всегда ли будет верно утверждение, что найдется часть, содержащая по крайней мере 2 точки с ?
Деление окружности
На окружности длины 1 мы отмечаем точку Р и откладываем от нее поочередно дуги иррациональной длины V. Таким образом получаем точки Р1, Р2, . . Рn, . . причем длина любой дуги всегда равна и. Точки Р1, Р2 . . ., Pn-1 делят окружность на n дуг. Доказать, что точка Рn окажется в наибольшей из них.
Лучи в пространстве
Три луча в пространстве исходят из общей вершины и образуют плоские углы А, В, С. Какие из неравенств!
1) A + В > С,
2) sin А + sin В > sin С,
3) sin 1/2 А + sin 1/2 В > sin 1/2 С,
4) sin2 А + sin2 В > sin2 С,
5) sin21/2 A + sin21/2 В > sin21/2 С
всегда верны, а какие - не всегда?
Неограниченная шахматная доска
На неограниченной шахматной доске ограничить фигуру, состоящую из 100 квадратов, т. е. из 100 клеток шахматной доски, таким образом, чтобы диаметр этой фигуры был по возможности наименьшим ( диаметром называется наибольшее расстояние между точками фигуры).
Найти этот диаметр. Найти радиус наименьшего круга, охватывающего 100 клеток шахматной доски.
Еще раз счеты
Пусть костяшки, о которых говорится в задаче 98, занумерованы от 1 до 10. В любом положении их проекции на основание счетов дают одну из возможных перестановок чисел 1, 2, 3 10. Пусть костяшки передвигаются по проволоке, как и в задаче 98, каждая с постоянной, но отличной от других скоростью, причем каждая скорость выражается целым числом см/с. Можно ли так подобрать эти скорости, чтобы - независимо от начального положения - счеты дали во время движения костяшек все возможные их перестановки (т. е. перестановки из чисел 1, 2, 3, . .., 10). Доктор Шарадек уверяет, что он знает такое распределение скоростей, при котором ни одна перестановка чисел не повторится, прежде чем не появятся все другие!
Сравнивание весов
Имеется четыре предмета разного веса, а также весы без гирь. На весах можно сравнивать вес любых двух предметов. Легко указать способ, который дает возможность установить порядок весов данных предметов самое большее после пяти взвешиваний. Доказать, что не существует такого способа, который бы гарантировал установление порядка весов предметов после четырех взвешиваний.
Известно, что для 10 предметов существует способ устанавливания порядка весов, требующий 24 взвешивания; можно ли это число взвешиваний уменьшить?
Банки в ящике
В ящике формы прямоугольного параллелепипеда, дно которого имеет размеры 186 мм на 286 мм, можно плотно уместить 16 одинаковых жестяных цилиндрических банок, имеющих высоту, равную высоте ящика, и стоящих основанием на дне его. Однако какое-либо увеличение диаметра банок уже не позволит их поместить в ящике. Каков диаметр банки?
Бактерии
Доктор Шарадек открыл вид бактерий, которые размножаются удивительным образом. От первичной бактерии отрывается часть и становится самостоятельной бактерией; обычно она короче оставшейся: таким образом, появляются две бактерии различной длины. От длиннейшей из них снова отрывается часть, тоже короче оставшейся, и этот процесс длится до тех пор, пока не приведет к остатку более короткому, чем какая-нибудь ранее оторванная часть. Тогда от длиннейшей из оставшихся отрывается часть, равная по длине кратчайшей из оставшихся. Это единственное правило (одновременно с неравным начальным разделением) достаточно для описания всего процесса размножения, однако нужно помнить, что в каждый момент самое большее одна бактерия делится на две.
Доказать, что в колонии бактерий никогда не бывает более трех различных длин, и если первое деление было иррациональным, то постоянно будут повторяться моменты, при которых окажутся всего только две различные длины, а также моменты, когда различных длин будет три, и, наконец, возможно такое первоначальное деление, при котором отношение длин сохранится при всех дальнейших делениях на части.
Подъезжает цирк!
Дети играют на лугу рядом с шоссе. Вдруг замечают в том месте, где шоссе выбегает из леса, шута на коне - это подъезжает цирк... Дети хотят подбежать к шоссе, чтобы увидеть шута; стоящие дальше уже не добегут, но хотят по крайней мере увидеть его как можно ближе. Все дети бегут с одинаковой скоростью, но шут едет быстрее.
Нужно: а) начертить линию, отделяющую ту часть луга, с которой можно добежать до шута, от остальной; б) определить путь бегущих детей, находившихся на этой линии; в) определить путь для детей, которые не добегут вовремя; г) найти путь детей, которые успеют добежать к шоссе прежде, чем шут их минует.
Тем, кто будет решать эту задачу, мы советуем познакомиться с задачей 89.
Три ковбоя
Три ковбоя охраняют стадо на большом квадратном пастбище. Ковбои хотят так разделить пастбище, чтобы: 1) каждый из них отвечал за поля, 2) самая дальняя точка пастбища, за которую отвечает ковбой А, находилась на таком же расстоянии от его поста, как и самая дальняя точка пастбища, охраняемого ковбоем В, от поста ковбоя В и самая дальняя точка пастбища, охраняемого ковбоем С, от поста ковбоя С. Кроме того ковбои хотели бы, чтобы: 3) это максимальное расстояние было по возможности наименьшим и 4) чтобы в случае какого-либо происшествия к месту происшествия всегда подъезжал ближайший из них.
Доказать, что задача неразрешима, и привести решение, которое можно получить, отбросив одно или же два условия.
Допрос
Судья: Итак, свидетель видел пожар? А что свидетель делал непосредственно перед пожаром?
Свидетель: Я ходил по межам.
Судья: Как проходят межи в вашей деревне?
Свидетель: Параллельно и перпендикулярно к шоссе.
Судья: Вы гуляли без цели?
Свидетель: Нет, идя от шоссе межами, я рассматривал поля соседей, ни разу не возвращался той же межой и снова вышел на шоссе.
Судья: А пересекали ли вы свою дорогу?
Свидетель: Нет. Но помню, что около рапса я проходил дважды, причем первый раз он был у меня по правую руку, так что я мог видеть дом, а когда проходил мимо него но второй раз, то он оказался по левую руку. Вот тогда я и услышал, что кричат "Горит!".
Судья велел арестовать свидетеля, как подозреваемого. Почему?
Стрелки на додекаэдре
Представим себе модель правильного додекаэдра, на каждой из его граней нарисуем стрелку → ; доказать, что найдутся две соседние стрелки, т. е. помещенные на смежных гранях, которые образуют угол, больший 90°.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'