Глава 6. Математические приключения доктора Шарадека

93. Удивительное число

Доктор Шарадек решил в корне изменить математическую запись. Он считает большим недоразумением то, что существует число, известное детям, начинающим учиться в школе, которое наряду с обычной записью имеет еще другую запись, о которой эти дети узнают лишь несколько лет спустя, а также еще и третью, очень сложную, о которой (к сожалению!) они узнают в более зрелом возрасте, причем никто им не говорит, что это - то же самое число. Только доктор Шарадек и его друзья знают этот секрет. Какое же это число?

94. "Сантиметр"

Портные называют "сантиметром" ленту с нанесенными на ней сантиметровыми делениями. Доктор Сильвестр Шарадек имеет (разумеется) иной "сантиметр", чем обычные смертные. Он выглядит так, как показано на рис. 3 (нарисована только часть ленты), т. е. в начале ленты он имеет оковку в полсантиметра. Доктор Шарадек утверждает, что его "сантиметр" лучше обычного. Почему?

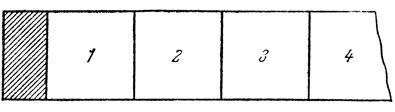
Рис. 3

95. Игра в слова

Доктор Сильвестр Шарадек объявил, что он всегда может отгадать загаданное слово, если ему будет разрешено задать 20 вопросов, отвечать на которые следует лишь словами "да" или "нет", и если загаданное слово имеется в словаре. Как вы думаете, не хвастает ли он?

96. Студенческие долги

Семь студентов живут в одной квартире. В течение всего "года они взаимно одалживают друг другу мелкие суммы денег. Доктор Сильвестр Шарадек посоветовал им, чтобы каждый отмечал у себя, сколько денег он взял взаймы и сколько дал взаймы, но не записывал, у кого или кому одолжил деньги. Перед отъездом на каникулы студенты решили рассчитаться друг с другом, однако они не знали, как это сделать. Достаточна ли такая бухгалтерия Шарадека для того, чтобы студенты могли расплатиться друг с другом? Сколько в худшем случае необходимо сделать выплат? {Выплатой мы называем вручение одному человеку какой-либо суммы денег другим человеком.)

96а. "Криптоним № 2"

Доктор Сильвестр Шарадек решает любые задачи. Друг Шарадека, который хотел его испытать, принес ему 12 однозлотовых монет, на вид одинаковых, и сказал: "Что касается одиннадцати, то я уверен, что они не фальшивые, но двенадцатая может быть фальшивой, однако я не знаю, легче она или тяжелее обычной". Говоря это, он высыпал монеты на стол и воскликнул: "Теперь я уже не знаю, которая из них подозрительная, но ты Сильвестр, наверное, обнаружишь это в результате трех взвешиваний, причем без разновесок, на обычных весах с двумя чашками". Шарадек ответил: "Я сейчас же это сделаю благодаря моему безошибочному методу, называемому "криптоним № 2"". Сказав это, он сложил монеты в ряд и написал на них мелом буквы K, R, Y, Р, Т, О, N, I, М, D, W, А, так что каждую монету обозначил одной буквой. Затем он проделал три взвешивания, каждый раз укладывая на весы сразу по четыре монеты на каждую чашку. Его приятель с удивлением заметил, что буквы сложились в слова:

Но через минуту лицо Шарадека потемнело от гнева. "Бесчестный обманщик! - воскликнул он,- ты хотел меня обмануть, меня, Сильвестра, Шарадека, доктора всех математических наук! Но это тебе не удалось, ибо мой "криптоним № 2" разоблачил тебя! среди твоих монет по крайней мере две фальшивые!" Его друг с раскаянием сознался, что он виновен.

Исследуйте, смог бы Шарадек, если бы не подвох, найти фальшивую монету и узнать, тяжелее она или легче настоящей монеты, а если бы все монеты были настоящими, сумел бы он обнаружить и это. Скажите, каковы были результаты взвешиваний, которые позволили мастеру заметить подвох. И, наконец, определите, мог ли приятель Шарадека так изменить массу двух монет (оставляя остальным монетам их настоящую массу), чтобы провести мастера вместе с его чудесным "криптонимом № 2".

96б. Кубики

Доктор С. Шарадек сообщил мне, что сто лет тому назад на царских именинах появилась делегация в составе 25 офицеров, по пять из пяти разных полков, причем каждый полк был представлен полковником, подполковником, майором, капитаном и поручиком, и генерал, возглавляющий делегацию, расставил ее Квадратным строем так, чтобы в каждом ряду стояли представители всех рангов и всех полков и так же в каждой колонне. Я спросил его, имели ли офицеры ордена, причем ордена пяти разных наименований так, чтобы каждый полк имел их все и каждый ранг имел их все, но каждый офицер - только один? Не сбитый с толку доктор Шарадек уверил меня, что именно так и было, что в каждой колонне и в каждом ряду были все ордена!

Перещеголяем фантазию знаменитого ученого и составим 125 кубиков в большой куб, обозначив предварительно каждый кубик цветом (белым, голубым, зеленым, красным и желтым), буквой ( А, В,С, D, Е) и номером (1, 2, 3, 4, 5) так, чтобы было по 25 кубиков каждого цвета, по 25 - каждой буквы и по 25 - каждого номера, а кроме того, так, чтобы каждый горизонтальный слой кубиков был моделью строя, аналогичного описанному выше, причем даже тогда, когда мы примем за горизонтальную плоскость любую грань большого куба.

97. Странное общество

Один человек рассказал, что однажды он оказался в обществе, состоящем (вместе с ним самим) из двенадцати человек, причем

а) каждый из них не был знаком с шестью другими людьми, но знал всех остальных;

б) каждый принадлежал некоторой тройке знакомых между собой людей;

в) среди собравшихся нельзя было выбрать четырех попарно знакомых людей;

г) среди собравшихся нельзя было выбрать также и четырех попарно незнакомых лиц;

д) каждый из собравшихся входил в тройку попарно незнакомых лиц;

е) каждый мог найти среди незнакомых ему людей человека, с которым он не имеет в этой компании общих знакомых.

Услышав этот рассказ, доктор Шарадек заявил, что однажды он был в обществе, в котором условия б), в), г), д) выполнялись, но каждый знал ровно 6 человек и имел знакомого, который мог познакомить его со всеми остальными.

Поясните эти ситуации.

98. Счеты

Представьте себе счеты, состоящие из 10 горизонтальных проволок, а на каждой проволоке по одной костяшке. Пусть эти костяшки передвигаются с постоянной скоростью, одинаковой для всех, туда и обратно по проволокам, меняя направление при ударе о сторону счетов. Начальное положение костяшек неизвестно. Вертикальная ось симметрии делит счеты на левую и правую половину. Пусть движение происходит так, что одновременно никогда не окажется более семи костяшек в правой половине счетов. Доктор Сильвестр Шарадек утверждает, что там никогда не окажется менее трех костяшек. Прав ли он?

99. Поливание улиц

Родной город доктора Шарадека имеет автоцистерну для поливания улиц, но не имеет подходящего гаража. Доктора попросили обозначить на плане города (который мы помещаем на рис. 4) самое лучшее место для гаража, т. е. такое, которое позволит кратчайшим путем объехать все улицы города и вернуться в гараж. Доктор Шарадек выбрал свой дом (на карте он обозначен темным квадратиком). Поступил ли он правильно?

Рис. 4

100. Французские города

Доктор Шарадек, знающий хорошо стратегию, интересовался последней войной и в 1940 году познакомился с картой французского театра военных действий. Отсюда, вероятно, и возникла следующая задача. Расстояние (по воздуху, как и все расстояния в этой задаче) от Шалона до Витри равно 30 км, от Витри до Шомона 80 км, от Шомона до Сэн-Кантэна 236 км, от Сен-Каитэна до Реймса 86 км, от Реймса до Шалона 40 км. Вычислить в этом замкнутом многоугольнике расстояние от Реймса до Шомона. Без карты это умеет сделать только Сильвестр Шарадек!