Глава 5. Шахматы, волейбол, погоня

77. Шахматная доска

Пусть квадратная или прямоугольная шахматная доска имеет нечетное число клеток (например, 49 или 63). Клетки с общей стороной будем называть смежными.

На каждой клетке шахматной доски расставляем по одной пешке, затем собираем пешки и снова расставляем на клетках шахматной доски.

Возможно ли, чтобы каждая пешка оказалась в клетке, смежной с той, которую она занимала первоначально?

78. Еще раз о шахматной доске

На каждой клетке шахматной доски ставим по пешке. Пешки собираем и расставляем заново, но так, чтобы пешки, стоявшие в левых углах, заняли свои прежние места и чтобы пешки, которые были соседними (т. е. занимали смежные клетки), снова стояли по соседству.

Возможно ли, чтобы какая-нибудь пешка оказалась на другом месте, чем первоначально?

79. Ладья на шахматной доске

Шахматная доска, которой мы воспользуемся, имеет столько же строк, сколько и столбцов, но отличается от обычной шахматной доски тем, что расположение белых и черных клеток может быть произвольным, лишь бы в каждом столбце была по крайней мере одна белая клетка и лишь бы по крайней мере один столбец был целиком белый. Будем говорить, что нам удалось расположить ладьи (а у нас их достаточный запас, так что недостатка в них не будет) на шахматной доске, если мы удовлетворим следующим условиям: 1) ладьи стоят только на белых клетках, 2) на шахматной доске стоит хотя бы одна ладья, 3) ладьи не атакуют друг друга (т. е. они стоят так, что не могут бить друг друга), 4) каждая белая клетка, не занятая ладьей, но находящаяся по горизонтали под угрозой ладьи, находится также под угрозой некоторой ладьи и по вертикали.

Доказать, что всегда можно расставить ладьи согласно требованиям 1), 2), 3) и 4).

80. Эллиптический бильярд

На эллиптическом бильярде шар А лежит у края, а шар В - на отрезке s, соединяющем фокусы эллипса. Нужно ударить шар А так, чтобы, оттолкнувшись от края, он столкнулся с шаром В; однако запрещается пересечение отрезка s шаром А перед ударом о край.

Доказать, что задача неразрешима.

81. Спортивная задача (I)

В классе 25 учеников. Из них 17 умеют ездить на велосипеде, 13 умеют плавать, а 8 - ходить на лыжах. Ни один из учеников не владеет всеми тремя видами спорта, но как велосипедисты, так и пловцы и лыжники имеют хорошие или удовлетворительные оценки по математике, что тем более знаменательно, так как шесть учеников имеют неудовлетворительные оценки по этому предмету.

Сколько учеников имеют отличные оценки по математике? Сколько пловцов умеют ходить на лыжах?

82. Спортивная задача (II)

Три бегуна А, В и С систематически состязались в беге на 200 метров, замечая после каждого пробега порядок, в котором они достигали финиша. Подводя итоги, они обнаружили, что в большинстве состязаний А обгонял В и что в большинстве случаев В бежал быстрее С, а также, что в большинстве случаев С приходил к финишу раньше А. Как это могло случиться?

83. Теория спортивных розыгрышей

Шахматный клуб доктора Сильвестра Шарадека насчитывает 10 членов. Ежегодно происходят розыгрыши с целью разделить игроков на классы. Каждый играет с каждым до первой результативной партии (ничьи не принимаются в расчет). Будем говорить, что "A выигрывает у В", если А выиграл у В в классификационном розыгрыше нынешнего года. Таких результатов после окончания турнира будет 45, а игроки разделятся на классы, например: на игроков, выигравших у восьмерых, выигравших у семерых, и т. д. (Заметим, что система 45 розыгрышей допускает возможность, что А выигрывает у В, В выигрывает у С и С выигрывает у Л.)

Вопрос касается возможных результатов классификации. В частности, возможно ли, чтобы клуб был разделен на три класса?

84. Объединение волейбольных команд

Лучшие команды по волейболу образуют объединение, которое устраивает сезонные встречи; каждая команда играет один раз с любой другой. Может случиться, что одна из команд победит все другие, но это не обязательно. Поэтому согласимся называть чемпионом такую команду, которая победила любую другую либо обычным путем, либо косвенно, т. е. через третью. Другими словами, будем считать, что команда А победила команду В, если существует команда С, проигравшая команде Л, но победившая в матче с В. Не будем, однако, считать косвенной победой команды А над В, если А побеждает С, С побеждает D,a D побеждает В.

Доказать, что 1) розыгрыши в объединениях всегда позволяют выявить одного или более чемпионов; 2) команда, которая непосредственно выиграла наибольшее число встреч, всегда является чемпионом.

85. Турниры

Так называемая кубковая система определения победителя из восьми спортсменов состоит в разбиении игроков на пары с помощью жеребьевки. Четыре матча определяют четырех победителей, которые участвуют во втором туре; третий тур соревнований является финалом. Победитель финального матча получает первый приз, а его соперник получает второй приз. Будем считать, что каждый игрок имеет определенную силу (подобно тому, как каждый предмет имеет определенный вес) и что более сильный игрок всегда выигрывает у более слабого (подобно тому, как более тяжелый предмет всегда перевешивает более легкий, если они помещены на разные чаши весов). В таких предположениях описанный выше процесс годен для определения чемпиона, так как победитель действительно будет сильнее всех своих соперников; однако второе место вовсе не всегда будет занято вторым по силе игроком.

Какова вероятность того, что второй участник финального матча в самом деле достоин второго приза?

86. Велосипедист и пешеходы

Директор совхоза отправил двух пеших посыльных: одного с письмом на почту в город, другого - на четверть часа позднее - в противоположном направлении, в соседний сельсовет. Но вдруг сообразил, что перепутал письма и выслал велосипедиста с поручением догнать обоих, исправить ошибку и вернуться. Велосипедист предполагает, что оба посыльных идут с одинаковой скоростью и колеблется, догнать ли сначала того, который вышел раньше, или того, который вышел позже. А так как он едет быстро, то в обоих случаях исполнит поручение.

Кто решит эту задачу, пусть скажет, каково было бы решение, если бы директор не перепутал писем, а только забыл бы дать посланцам деньги и хотел бы это исправить.

87. Четыре собаки

Четыре собаки А, В, и стоят в углах квадратного луга и вдруг начинают гоняться друг за другом, как указывают стрелки на рис. 2.

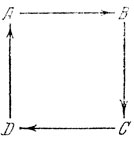
Рис. 2

Каждая собака бежит прямо к соседней: А к В, В к С, С к D, D к А. Сторона луга равна 100 м, а скорость бега собак равна 10 м/с.

Через какой промежуток времени собаки встретятся? Пересекутся ли их пути и где? Какова длина каждого пути?

88. Погоня (I)

Корабль Р заметил корабль Q, который плывет в направлении, перпендикулярном к PQ, сохраняя свой курс. Корабль Р гонится за Q, постоянно направляясь к Q; скорость обоих кораблей в каждый момент одинакова (но может изменяться со временем). Без вычислений видно, что Р плывет по кривой линии; если погоня длится Достаточно долго, то траектория догоняющего корабля и траектория убегающего корабля в конце концов становятся почти идентичными. Каково будет тогда расстояние PQ, если в начале оно было равно 10 морским милям?

89. Погоня (11)

Корабль О₁ замечает другой корабль O₂, плывущий в момент наблюдения перпендикулярно к прямой О_1О2. Корабль O₂ не замечает сигналов и сохраняет свой первоначальный курс и свою скорость v₂. Корабль Ох хочет обратить на себя внимание, так как ему необходима помощь, и с максимальной скоростью на которую он только способен, плывет в таком направлении, чтобы как можно ближе подойти к O₂. Какой он должен взять курс? Каково будет расстояние между обоими кораблями в момент наибольшего сближения, если начальное расстояние было равно d, а отношение скоростей v₁/v₂ равно k и меньше 1?

90. Действительно ли условия задачи неполные?

Кто-то, не очень внимательно прочитав предыдущую задачу, рассказал ее доктору Шарадеку и спросил, как определить курс, исходя из условий задачи. К сожалению, он забыл, какой из кораблей имеет большую скорость, а какой - меньшую, но помнил, что отношение скоростей k известно и меньше 1. Однако он не знал, означает ли k отношение скорости сигнализирующего корабля к скорости замеченного корабля или наоборот. И велико же было его изумление, когда доктор Шарадек тотчас же определил курс на основе неполных данных! Каким образом доктор Шарадек сделал это?

91. Моторная лодка (I)

Моторная лодка контрабандистов имеет втрое большую скорость, чем сторожевой корабль, находящийся на расстоянии половины пути от лодки к тому месту побережья, до которого лодка хочет добраться. Капитан лодки решает плыть к цели вдоль двух сторон квадрата. Какая часть этого пути будет опасной?

92. Моторная лодка (II)

В предыдущей задаче капитан лодки решил плыть так, чтобы по пути один раз изменить курс на 90°. Какой он должен выбрать путь, чтобы наверняка обойти сторожевой корабль и как можно быстрее достигнуть цели?