
Решения задач
1. Прежде всего заметим, что в данной последовательности каждая нечетная цифра может появиться только между двумя четными цифрами.
Действительно, предположим, что два последовательных члена с, d рассматриваемой последовательности - нечетные. Тогда могут иметь место два случая:
или число c̄d̄ является произведением двух членов а, b данной последовательности, предшествующих членам с, d и нечетных,
или же цифра с является последней цифрой произведений двух членов а, b данной последовательности, предшествующих членам с,d и нечетных.
Таким образом, из предпосылки, что два последовательных члена с, d рассматриваемой последовательности являются нечетными, следовало бы, что два других члена этой последовательности, предшествующие членам с, d, являются нечетными. Поэтому из предпосылки, что два последовательных члена с, d рассматриваемой последовательности являются нечетными, следовало бы, что среди трех начальных цифр данной последовательности имеются две нечетные, что в действительности не имеет места.
Из приведенного замечания, что в рассматриваемой последовательности никогда не выступают два соседних нечетных члена, следует, что цифра 9 в данной последовательности не появится. Действительно, цифра 9 могла бы появиться только в произведении двух чисел не меньшем 90, а произведение двух однозначных чисел всегда меньше 90.
Не может также появиться и цифра 7, так как единственным двузначным произведением однозначных чисел разной четности, в котором появляется цифра 7, является произведение 8×9=72, но цифры 9 в данной последовательности нет.
Мы не встретим также в этой последовательности и цифры 5, ибо только два произведения однозначных чисел разной четности содержат цифру 5, а именно, 54=6*9 и 56=7*8, но оба они содержат такие цифры, которые не появляются в данной последовательности.
2. Обозначим произвольное натуральное n-значное число через
L = 10n-1an + 10n-2an-1 + ... + 102a3 + 10a2 + a1
а сумму квадратов его цифр через
L1 = a2n + a2n-1 + ... + a23 + a22 + a21
Имеем
L - L1 = (10n-1-an)an+(10n-2-an-1)an-1+...+ (103-a4)a4+(102-a3)a3 + (l0-a2)a2 -(a1 - 1)a1.
Заметим, что
(a1-1)a1 ≤ 72,
Таким образом, если мы предположим, что n ≥ 3 то (так как an≠0) будем иметь
(10n-1-an)an≥99,
вместе с тем
(10i-1-аi)ai для i = 2, 3,..., n - 1,
поэтому
L>L1
Из последнего неравенства вытекает, что, исходя из данного по меньшей мере трехзначного числа L и образуя описанным в задач* способом последовательность
L1, L2, L3,... (1)
сумм квадратов цифр, мы получим убывающую последовательность, пока члены этой последовательности будут по меньшей мере трехзначными; а так как они могут быть только натуральными, числами, то, исходя из произвольного числа L, в котором не менее трех цифр, после некоторого числа шагов описанного в задаче процесса наверняка придем к не более чем трехзначному числу. Отсюда следует, что достаточно проверить, верно ли утверждение задачи для чисел самое большее трехзначных.
Предположим, следовательно, что дано трехзначное число L, т, е, что n=3. Тогда a3≠0 и получаем
L-L1 = (100-a3)a3 + (10-a2)a2 - (a1-1)a1≥99-72=27
или
L1≤L-27
Из последнего неравенства вытекает, что некоторый член последовательности (1) является самое большее двузначным числом. Пусть этим членом будет
Lq = 10j + k.
Так как члены последовательности L,
Lq+1, Lq+2, Lq+3,.....
не изменятся, если число Lq заменим числом 10k+j, то наше предположение достаточно доказать для чисел Lq при условиях
j≥k≥0, j≥1
Если Lq = 10j+k, а также j≥k≥ и j≥1, то Lq+1 является одним из чисел следующей таблицы значений выражения j2+k2:
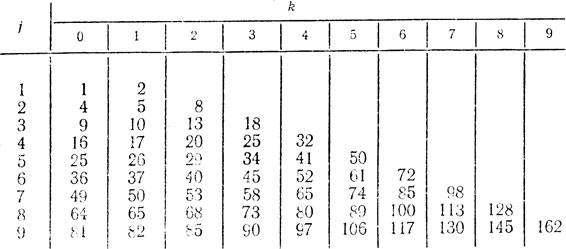
Из этой таблицы мы можем отбросить числа
1, 10, 100,
а также названные в условии задачи числа
145, 20, 4, 16, 37, 58, 89,
так как для них теорема верна. Кроме того, мы можем отбросить числа
2, 40, 50, 52, 61, 73, 80, 81,85, 90, 98, 130,
которые отличаются от предшествующих чисел или же от других чисел таблицы перестановкой цифр или же приписыванием цифры 0. Тогда останется 28 чисел, а именно,
5, 8, 9, 13, 17, 18, 25, 26, 29, 32, 34, 36, 41, 45, 49, 53,
64, 65, 68, 72, 74, 82, 97, 106, 113, 117, 128, 162,
для которых нужно проверить достоверность теоремы.
Результаты проверки запишем в таблицу. В первом столбце запишем число, для которого проверяем теорему, а во втором столбце запишем поочередно члены последовательности (1), образованной именно для этого числа. Проверку прервем, если дойдем до одного из чисел, для которых теорема верна.
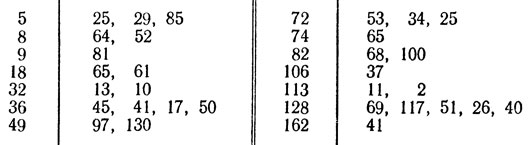
Так как в каждом случае в конце концов приходим к числу 1 или же к одному из чисел
145, 42, 20, 4, 16, 37, 58, 89,
которые периодически повторяются, то указанная в задач'е теорема доказана.
3. При делении степеней 5α, 4β, 3γ на 11 (где α, β, γ обозначают целые неотрицательные числа., не превышающие 5) получаем следующие остатки:
Число Остаток Число Остаток Число Остаток
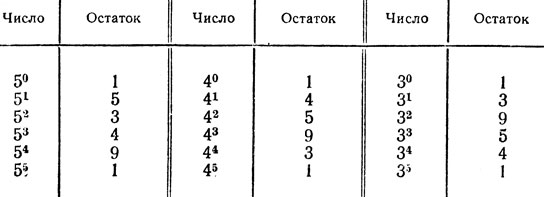
Обозначим соответственно через R (5α), R (4β), R (3γ) остатки, полученные от деления чисел 5α, 4β , 3γ на 11. Остатки эти можно прочесть по приведенной выше таблице. Обозначим, далее, через k, m, n три производных неотрицательных целых числа. Числа 55k, 45m, 35n при делении на 11 дают в остатке единицу. Поэтому числа 55k+α, 45m+β, 35n+γ при делении на 11 дают соответственно остатки R(5α), R(4∩), R(3γ). В таком случае выражение
55k+α + 45m+β + 35n+γ (1)
только тогда делится на 11, когда сумма R (5α) + (4β) + (3γ) делится на 11. Это имеет место при
k=m=n, α=1, β=2, γ=0.
Можно привести 14 других выражений типа (1), делящихся на 11. Их находят, выбирая из трех столбцов приведенной выше таблицы по одному числу так, чтобы в сумме получить число, делящееся на 11.
4. Выражение an+bn делится на a+b, если n - нечетное число. Потому число
3105+4105=(33)35+(43)36
делится на 33+43=7*13. Аналогично из равенств
3105+4105=(35)21+(45)21
3105+4105=(37)15+(47)15
следует, что данное число делится на 35+45=7*181 и на 37+47=49*379, Заметим, далее, что
43≡-1 (mod 5)
(эта формула обозначает, что число 43 при делении на 5 дает остаток -1). Отсюда вытекает, что
4105≡(-1)35(moi 5)
следовательно,
4105≡-1 (mod 5).
Подобным же образом 32≡-1 (mod 5), отсюда следует, что
3104≡(-1)52(mod 5),
следовательно,
3104≡1 (mod 5) и 3105≡3 (mod 5).
Так как
4105≡-1 (mod 5) и 3105≡3(mod 5), то
3105+4105≡2 (mod 5);
это означает, что число 3105+4105 при делении на 5 дает в остатке 2. Подобным же образом
43≡-2 (mod 11), откуда 415≡-32 (mod 11), а так как - 32≡1 (mod 11), то
415≡ 1 (mod 11)
и, в конечном счете,
4105≡51 (mod 11).
Точно так же убеждаемся в том, что
35≡1 (mod 11), откуда 3105= 1(mod 11).
Поэтому
3105+4105≡2 (mod 11);
это означает, что число 3105+4105 при делении на 11 дает в остатке 2,
5. Пусть существуют натуральные числа х, y, r, n такие, что и xn+yn=zn. Нетрудно заметить, что x<z, y<z и х≠y, ввиду симметрии можно предположить, что х<y, тогда
zn-yn = (z-y)(zn-1+yzn-2+...+yn-1)≥1*nxn-1>xn,
вопреки нашему предположению, что xn+yn=zn. Отсюда следует справедливость сформулированного в задаче утверждения.
6. Можно привести много последовательностей чисел х1, х2,...,x10 удовлетворяющих условиям задачи. Вот две из них:
Числа первой из этих последовательностей располагаются следующим образом в частях отрезка [0, 1]:

Эта таблица имеет следующий смысл. В столбце, помеченном сверху числом 2, в первой строке выписано число 2, а во второй - 1; это указывает на то, что 0,05 принадлежит первой половине отрезка [0, 1], а 0,95 - второй половине этого отрезка. Сказанное переносится, разумеется, на любой столбец таблицы. Так, например, 6 в столбце, помеченном сверху числом 8, принадлежит строке, в левом столбце которой стоит дробь 0,74; это указывает на то, что 0,74 принадлежит 6-й из тех частей отрезка [0, 1], которые мы получаем при делении его на 8 равных частей (т. е. что 5/8<0,74<6/8). Нетрудно проверить справедливость всех просуммированных в этой таблице данных. Поскольку в каждом столбце мы имеем ровно столько чисел, сколько указывает число вверху этого столбца, причем все стоящие в одном столбце числа различны, то условия задачи выполнены.
7. Система 14 чисел (n=14), удовлетворяющих условиям аналогичным приведенным в предыдущей задаче, существует:
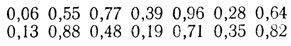
(она возникает путем дописывания чисел 0,19, 0,71,0,35, 0,82 ко второй последовательности, приведенной в предыдущей задаче).
Расположение чисел этой системы в отрезке [0, 1] следующее:

Так как числа 0,35 и 0,39 находятся между 5/15=0,33... и 6/15=0,4, то приведенную выше систему уже нельзя дополнить пятнадцатым числом с сохранением условия задачи.
Любопытно, что числа системы можно переставить таким образом, чтобы условие задачи по-прежнему было выполнено, например:
0,19 0,96 0,55 0,39 0,77 0,06 0,64
0,28 0,88 0,48 0,13, 0,71 0,35 0,82,
А. Шинцель показал, что в общем случае ответ на вопрос задачи отрицательный, следующим образом установив неразрешимость ее для случая n=75*).
Предположим, что числа х1, х2,..., х75 удовлетворяют требуемым условиям. Тогда для некоторых натуральных i<j≤35 имеем
7/35<xi<8/35,
9/35<xj<10/35 (1)
Следовательно,
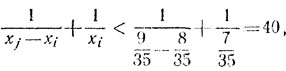 (2')
(2')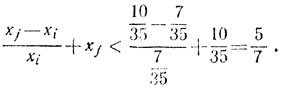 (2)
(2)Пусть
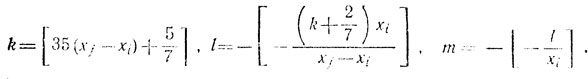
* (М. Вармус (М. Warm us) доказал, что последним значением n, для которого задача разрешима, является n=17.)
Через [х] здесь, как всегда, обозначается целая часть числа х; другими словами,
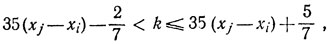 (3)
(3)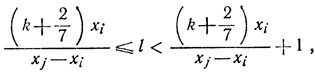 (4)
(4)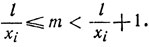 (5)
(5)Из (3) и (4) следует, что
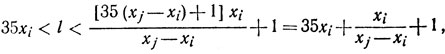
а сопоставив (5) и (2'), мы получим
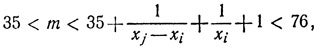
или
36≤m≤75. (6)
Из неравенства (5), кроме того, следует, что (m-1)хi<l<mxi
[(m-1)xi]<[mxi] (7)
С другой стороны, в силу (5), (4) и (1),
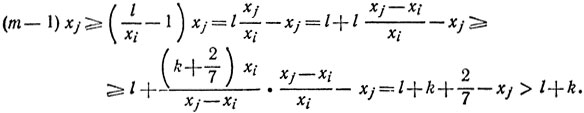
Аналогично, в силу (2)
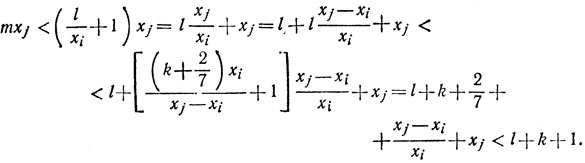
Комбинируя полученные неравенства, мы найдем, что
l+k<(m-1)xj<mxj<l+k+1
откуда
[(m-1)хj] = [mхj]. (8)
Из (7) и (8) следует, что
Nm-1 = [(m-1)xj] -[(m-1)хi] > [mxj] - [mxi] = Nm. (9)
Однако из условия задачи и из неравенства (6) следует, что последовательность чисел [(m-1)лx1], [(m-1)х2], ...., [(m-1)xm-1] получается из последовательности 0, 1,..., m-2 простой перестановкой входящих в нее чисел и, аналогично, последовательность [mx1], [mx2],..., [mxm] получается перестановкой из последовательности 0, 1, ..., m-1.
Так как t, j≤35≤m-1, Nm-1 - это число решений неравенства xi<xt<xj в натуральных числах t≤m-1 и Nm - число решений этого неравенства в натуральных числах t≤m. Следовательно, Nm-1≤Nm, что противоречит неравенству (9). Это противоречие и завершает доказательство.
7а. Существует 90 перестановок. Однако если мы будем считать перестановки, полученные путем замены букв, отличающимися несущественно, то получим только 90 : 6=15 различных групп перестановок, ибо существует 6=3! перестановок букв а, b, с: abc acb bac bca cab cba.
Выпишем из каждой из этих 15 различных групп перестановок одну перестановку, именно ту, в которой первой буквой является а, второй, отличной от а, буквой является b, а третьей, отличной от предыдущей буквы, является буква с:

Рядом с каждой перестановкой мы выписали в скобках представителя и номер той группы перестановок, которую мы получаем из перестановок данной группы, прочитывая их с конца. В качестве представителя мы подбираем такую перестановку, в которой первой буквой является а, второй, отличной от нее, буквой будет b, а третьей, отличной от предыдущих, будет буква с.
Совершенно очевидно, что группы 4, 7, 8 и 12 (отмеченные звездочками) не отличаются существенно соответственно от групп 2, 3, 6 и 11, если прочитывать их с конца. Поэтому групп перестановок, отличающихся существенно, всего 11. Их них 7 групп содержат по 6 перестановок, а 4 группы - по 12 перестановок.
8. Можно принять
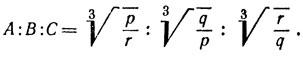
Действительно, в силу легко доказываемого равенства
pqr = 1
имеем
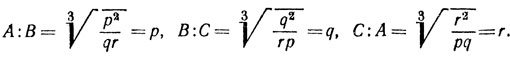
Используя вторично равенство pqr = 1, мы можем из приведенной - выше пропорции получить другую, также обладающую требуемыми свойствами:
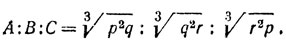
8а. Обозначим выражение, симметричность которого следует доказать, буквой w. Легко заметить, что
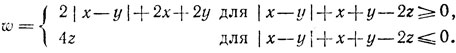
Рассматривая еще случай х-y≥0 и х-y≤0, заключаем, что
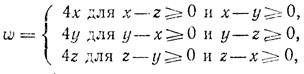
т. е. w = 4 max {х, y, z}, откуда непосредственно следует симметричность этого выражения,
9. Для x>0 левая часть уравнения возрастает с возрастанием х, и легко заметить, что при х=1,5 она меньше 10, а при х=1,6 - больше 10. Поэтому корень уравнения лежит внутри интервала (1,5, 1,6). Запишем его как неприводимую дробь p/q. Тогда уравнение примет следующий вид: p5+pq4 = 10q5, откуда следует, что р - делитель числа 10, следовательно, р равно одному из чисел 1, 2,5, 10. Однако выписывая дроби с вычислителями 1, 2, 5, 10, сразу же замечаем, что ни одна из них не попадает внутрь интервала (1,5, 1,6).
10. Заметим сначала, что имеет место следующая лемма: если р, q, х, y - положительные числа, то неравенства
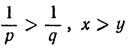
влекут за собой неравенство
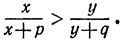
Действительно, по условию
1/p > 1/q > 0 и x > y > 0
поэтому x/p > y/p > 0, следовательно,
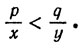
В таком случае
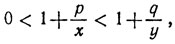
или
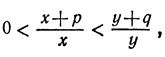
следовательно,
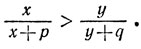
Таким образом, лемма доказана.
Так как А, В, С, а, b, с, r - положительные числа, то
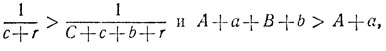
поэтому, согласно доказанной лемме,
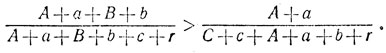 (1)
(1)Подобным же образом получаем
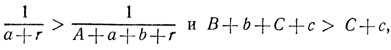
а следовательно, в силу доказанной леммы,
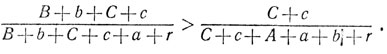 (2)
(2)Складывая неравенства (1) и (2), получим неравенство, правильность которого мы и должны были доказать.
11. Уравнение 1-z=z2 имеет один и только один положительный корень z=(√5-1)/2. Следовательно, это z удовлетворяет уравнениям
1-z=z2, z-z2=z3,.....,zn-zn+1=zn+2
Обозначив число zn через an(n = 0, 1, 2, ...) мы получим нужную нам последовательность. Так как 0<z<1, предел этой последовательности (геометрической прогрессии) равен 0.
Пусть теперь b0, b1 ... - другая последовательность, удовлетворяющая условиям задачи, т. е. такая, что b0=1 и bn-bn+1=bn+2 при n = 0, 1, ... Если эта последовательность отлична от построенной выше геометрической прогрессии, то найдется некоторый ее элемент bk, отличный от zk, т. е. такой, что bk=zk+d, где 0. Пусть k - первый номер такой, что bk≠zk так как b0=1=z°, то и, значит, существует элемент k≥1 второй последовательности, совпадающей с элементом zk-1 первой последовательности: bk-1=zk-1. Таким образом, мы имеем
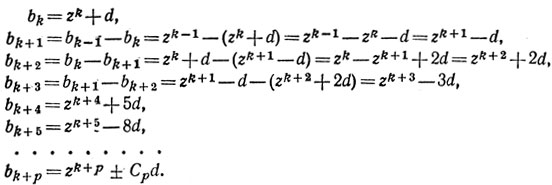
Поскольку zk+p стремится к 0 при p→∞, то для достаточно больших р знак элемента bk+p определяется знаком выражения ±Cpd, абсолютная величина которого заведомо не меньше d. Но целые числа ±Ср (коэффициенты при d) попеременно положительны и отрицательны, а значит, в последовательности {bn} встретятся как положительные, так и отрицательные числа, что противоречит условию задачи. Таким образом, предположение о несовпадении последовательностей {bn} и {zn } приводит к противоречию и, следовательно, последовательность {zk} доставляет единственное решение задачи.
12. Предположим, что полученная фигура содержит замкнутый многоугольник ABCDE...MN.
Предположим, кроме того, что AN<AB, т. е. что точка А соединена с точкой N, как с самой ближайшей. Тогда АВ<ВС. Но точки В и С соединены отрезком, следовательно, BC<CD. Рассуждая подобным же образом, получим, далее, что CD<DE<...<MN<NA, т. е. что AB<NA, а это противоречит нашему предположению, что AN<AB.
Так как при условии, что AN>AB, можно рассуждать подобным же образом, то сделанное нами предположение ведет к противоречию. Отсюда следует, что наша фигура не может содержать замкнутого многоугольника.
II. Предположим, что образованная фигура содержит два пересекающихся отрезка АВ и CD (рис. 5).
Допустим, что точки А к В потому были соединены отрезками, что точка В ближе всего расположена к точке А и что точка D ближе всего расположена к точке С. Тогда
AB<AD, CD<CB,
откуда
AB+CD<AD+CB,
что противоречит утверждению, что в выпуклом четырехугольнике сумма диагоналей больше суммы его двух противоположных сторон.
Таким образом, мы доказали и вторую часть теоремы.
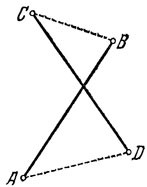
Рис. 5
13. Для упрощения введем следующие обозначения:
r=√(x21+...+x2k-1), a=xk, b=xk+1
Докажем, что если а<b, то порядок
x1, x2,...,xk-1, b, a, xk+2,...,xn
дает меньший угол, чем первоначальный порядок
x1, x2,...,xk-1, a, b, xk+2,...,xn
С этой целью достаточно сравнить углы Pk-1OPk+1 в обоих порядках. На рис. 6 угол P'k+1OPk-1 отвечает первоначальному порядку, а угол P'k+1OPk-1 - измененному порядку. Так как OP'k+1=OP'k+1(=√(r2+a2+b2)), то следует доказать неравенство P'k+1R"<P'k+1R' т. е. неравенство
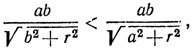
которое вытекает из предположения, что а<b,
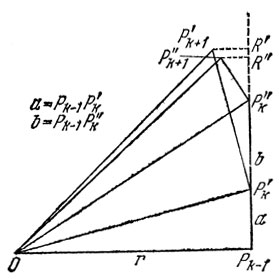
Рис. 6
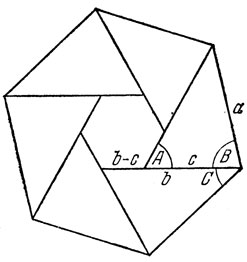
Рис. 7
14. Если в треугольнике АВС со сторонами а, b, с дан ∠A=60°, то ∠B+∠C=120°, и шесть таких треугольников можно уложить венком (рис. 7), ограниченным извне правильным шестиугольником со стороной а, а изнутри правильным шестиугольником со стороной Ъ-с. Вычисляя площади обоих Шестиугольников, получим формулу (1), данную в условии задачи.
В случае, когда в треугольнике дан ∠A=120° то ∠B+∠C=60°; три таких треугольника укладываются в треугольный венок (рис. 8). Рассуждение, подобное предыдущему, дает формулу (2).
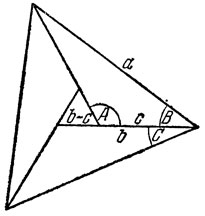
Рис. 8
15. Проведем прямую, которая пересечет стороны А1А2 и А3А1 треугольника А1А2А3 и разделит его периметр, равный 2р, пополам (рис. 9). Примем прямые А1А2 и А1А3 за координатные оси и пусть прямая С3С2 пройдет через точки С3 (q+λ, 0) и С2(0, q-λ), где q=1/2р, а λ - произвольное число. Прямая С3С2, конечно, делит пополам периметр треугольника А1А2А3.
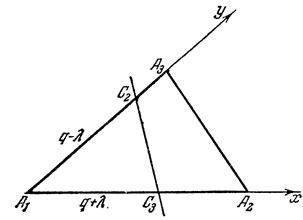
Рис. 9
Из условия, что прямая С3С2 пересекает стороны А1А2 и А3А1 а не их продолжения, получаем
0≤q+λ≤d3
0≤q-λ≤d2
откуда
 (1)
(1)Совершенно очевидно, что из неравенства d1<d2+d3 следует неравенство 2d12p, или d1<p, и что подобным же образом d2p, d3<p. Видно также, что из неравенства p>d3 следует неравенство q>d2-q и что подобным же образом из неравенства p>d2 получаем неравенство q-d2>-q. Поэтому систему неравенств (1) мы можем заменить двойным неравенством
q-d2 ≤ λ ≤ d3-q, (2)
определяющим допустимые значения параметра λ. Уравнение прямой С3С2 имеет вид
(q-λ)λ+(q+λ)y-q2+λ2=0. (3)
Если, начертив треугольник А1А2А3 мы измерили бы его периметр 2р, а затем, поочередно подставляя различные числовые значения вместо параметрах, определили для каждого значения λ точки С3, С2 и начертили прямую С3С2, то мы бы убедились (рис, 10), что все прямые С3С2 касательны к одной и той же кривой, которая является огибающей семейства прямых (3). Нетрудно подсчитать, что уравнением этой кривой будет
4ху = (p-x-y)2. (4)
Кривая (4) - парабола, ибо это - кривая второго порядка, которая с каждой прямой, определенной уравнением y=x+k, имеет,
независимо от значения параметра k, только одну общую точку. Поэтому ось параболы (4) параллельна прямой y-х, т. е. биссектрисе угла А1. Подставляя в уравнение (4) вместо х и y поочередно значения y=0 и х=0, мы убедимся, что парабола (4) касается сторон угла А1 в точках Т3(р, 0) и T2(0, р), как показано на рис. 11. А так как треугольник А1T2Т3 равнобедренный, то биссектриса угла A1 перпендикулярна к Т2Т3 и делит этот отрезок пополам, т. е. является осью параболы (4).
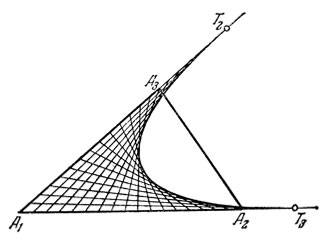
Рис. 10
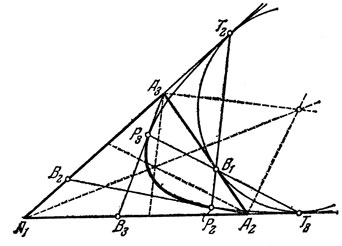
Рис. 11
Подставляя теперь поочередно крайние значения параметра λ, определенные неравенствами (2), получим при λ=q-d2 прямую А3В3 касательную к параболе (4) в точке Р3 с координатами
x=(p-d2)2/p, y=d22/p
а при λ=d3-q прямую А2В2, касательную к параболе (4) в точке Р2 с координатами
x=d23/p, y=(p-d3)2/p
причем A1B3=p-d2, B3A2=p-d1, A1B2=p-d3, B2A3=p-d1. Если через В1 обозначить точку, делящую сторону А2А3 на отрезки р-d3 и р-d2, то нетрудно проверить, что точки Т2, В1, Р2, а также точки T3, В1, Р3 расположены на одной прямой. Видно также, что прямые Т2В1 и Т3В1 соответственно параллельны биссектрисам углов А3 и А2. И, наконец, можно заметить, что окружность, проходящая через точки B1, Т2, T3, касается в них прямых А2А3, A3T2, A2T3.
Итак, каждая прямая, делящая периметр треугольника А1А2А3 пополам и пересекающая стороны треугольника А1А2 и A3A1 касательна к дуге параболы (4), и наоборот.
То же рассуждение можно применить к каждому из трех углов треугольника. Таким образом, получим три дуги параболы, которые вместе с отрезками общих касательных составляют криволинейный треугольник T (рис. 12).
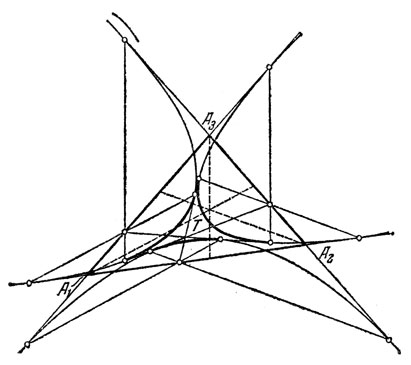
Рис. 12
Теперь мы можем сформулировать следующие выводы.
1° Через каждую точку Р, лежащую внутри треугольника А1А2А3, но вне треугольника T, проходит одна и только одна прямая, делящая периметр данного треугольника пополам. Это - касательная, которую из точки Р можно провести к одной из трех дуг параболы, указанных на рис. 12.
2° Через каждую точку Р, лежащую внутри треугольника T, проходят три и только три прямые, делящие периметр данного треугольника А1А2А3 пополам. Это - три касательные, которые из точки Р можно провести к дугам парабол, указанных на рис. 12.
3° Если на плоскости дано направление, то всегда можно провести параллельную ему прямую, делящую периметр треугольника пополам, С этой целью достаточно провести по данному направлению касательную к одной из дуг данной параболы.
4 Если даны два направления, то можно всегда провести две параллельные этим направлениям прямые, каждая из которых делит периметр треугольника пополам. Общая точка Q этих прямых лежит внутри криволинейногр треугольника T, вследствие чего всегда, когда даны две прямые, делящие периметр данного треугольника пополам, через их точку пересечения Q можно провести третью прямую, делящую периметр данного треугольника пополам.
5° Если дана система трех прямых l1, l2, l3 (рис. 13), жестко связанных между собой (например, начерченных тушью на целлофане), то всегда можно так расположить эту систему на плоскости, чтобы каждая из прямых l1, l2, l3 делила периметр треугольника А1А2А3 пополам.
Решение задачи дало довольно неожиданный результат: точку, обладающую требуемым свойством, совсем не нужно искать, так как каждая точка Q, о которой говорится в задаче, обладает этим свойством.
Если бы мы треугольник заменили другой фигурой, например четырехугольником, то задача решалась бы подобным же образом. Правда, вместо криволинейного треугольника Т получилась бы область, ограниченная четырьмя дугами парабол, но, как и прежде, через каждую точку, лежащую внутри четырехугольника, можно было бы - так же как и в треугольнике - провести одну или три прямые, делящие периметр пополам. Если же фигура имеет центр симметрии, то область, состоящая из точек, через которые можно провести три прямые, делящие периметр пополам, сводится к одной точке, и каждая прямая, проходящая через эту точку, делит периметр пополам.
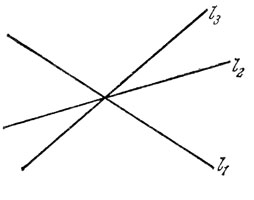
Рис. 13
15а. Сначала напомним, что центр масс трех произвольных точек одновременно является и центром масс треугольника, вершинами которого служат эти точки. Воспользуемся этим свойством и разделим треугольник АВС на треугольники ВСР, САР и АВР (рис. 14), и массы каждого из них поместим в их центрах масс А1, В1 и С1. Эти массы равны, так как равны площади треугольников ВСР, САР и АВР (почему?), следовательно, Р есть центр масс трех точек А1, B1 , C1.
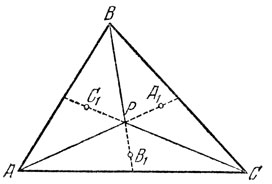
Рис. 14
16. Чтобы разделить треугольник на некоторое число треугольников так, чтобы в каждой вершине образованной фигуры сходилось одинаковое число сторон, воспользуемся правильными многогранниками, грани которых являются треугольниками. Это могут быть следующие многогранники: правильные тетраэдр, октаэдр и икосаэдр, и только они.
Если внутри тетраэдра мы выберем точку, лежащую близко от центра одной из граней, и из этой точки спроектируем ребра тетраэдра на плоскость, то получим фигуру, изображенную на рис. 15. Она состоит из трех треугольников, соответствующих граням тетраэдра; четвертая грань при проектировании перешла в большой треугольник АВС. В каждой вершине фигуры сходятся три стороны, так как в каждой вершине тетраэдра сходятся три ребра.
Подобным же образом, при помощи центральной проекции, получим из правильного октаэдра фигуру, состоящую из семи треугольников, в каждой вершине которой сходится четыре стороны (рис. 16), а из правильного икосаэдра - фигуру, состоящую из 19 треугольников, в каждой вершине которой сходится пять сторон (рис. 17).
Рис. 15
Рис. 16
Рис. 17
Не существует фигуры, отвечающей условиям задачи и отличающейся от изображенных на рис. 15-17, так как ей соответствовал бы правильный многогранник, отличающийся от трех приведенных выше, а такого не существует - ср. со сказанным в книге "Математический калейдоскоп"* о так называемых Платоновых телах (или "правильных многогранниках"): правильные многогранники с треугольными гранями бывают только трех типов, отвечающих рис. 15-17; соответствующие значения числа F частей плоскости (= числу граней многогранника) суть 4, 8 и 20**.
* (Штейнгауз Г. Математический калейдоскоп.- М.: Наука, 1981, с. 98-101.- Примеч. ред. )
** ( Относительно доказательства этого см., например, Радемахер Г., Тепл ицО. Числа и фигуры.- М.: Наука, 1966, тема 14.- Примеч. ред. )
17. Ответ на поставленный в задаче вопрос положителен. Так как имеется только конечное число прямых, каждая из которых проходит через какие-нибудь две точки из данных 3n точек, то мы можем выбрать прямую, не проходящую ни через одну из данных 3n точек так, чтобы все эти точки лежали по одну сторону от нее. Если будем передвигать эту прямую по плоскости, не изменяя ее направления, то все точки сначала будут лежать по одну сторону прямой, потом она поочередно минует точки первую, вторую, третью, ..., 3n-ю. Прямая, после того как она минует 3, 6, ..., 3n - 3 точек, делит плоскость на полосы, а в каждой из этих полос лежит только один треугольник.
Точно таким же образом можно построить не пересекающиеся и не вмещающие друг друга четырехугольники, пятиугольники и т. д.
18. Ответ на поставленный в задаче вопрос положителен: в узлах сети можно поместить знаки плюс, минус так, чтобы условие задачи было выполнено.
Начнем с замечания, что если решение задачи существует, то могут иметь место только два случая:
1) в трех вершинах каждого равностороннего треугольника находятся только знаки плюс (рис. 18),
2) в двух вершинах каждого треугольника находятся знаки минус, а в одной вершине - знак плюс (рис. 19).
Первый случай исключается.
Присоединяя к треугольникам как на рис. 19 отрезки, отмеченные одинаковыми знаками, и соответствующие треугольники, мы можем построить бесконечную полосу (рис. 20).
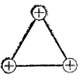
Рис. 18
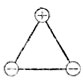
Рис. 19
Мы видим, что по краям этой полосы в вершинах треугольников поочередно выступают: знак плюс, затем два знака минус - и дальше в том же порядке.
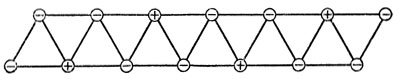
Рис. 20
Отсюда следует, что, складывая соответственным образом такие же полосы, мы можем всю плоскость покрыть сетью равносторонних треугольников, удовлетворяющей условию задачи (рис. 21). Из построения сети, отвечающей условию задачи, следует, что размещение знаков плюс и минус в узлах этой сети единственно.
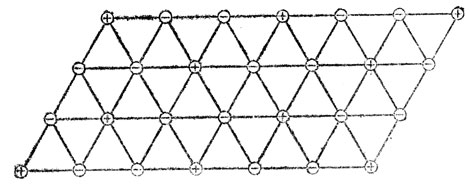
Рис. 21
19. Предположим обратное, т. е. что можно покрыть плоскость сетью треугольников так, чтобы в каждом узле W сходилось пять треугольников (рис. 22). Тогда сумма углов при вершине W четырех произвольных из этих пяти треугольников должна была бы быть больше 180°.
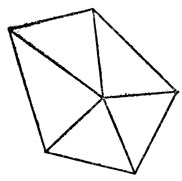
Рис. 22
Возьмем произвольный треугольник Т, принадлежащий сети (рис. 23). Тогда треугольники сети, которые имеют с треугольником Т по крайней мере одну общую точку, образовали бы шестиугольник S (рис. 24), в трех вершинах которого A1, А2, А3 сходилось бы по три треугольника, а в трех остальных вершинах В1, В2, В3 - по два треугольника. К шестиугольнику S в вершинах А1, А2, А3 прилегало бы по два треугольника (рис. 25), а в вершинах В1, В2, В3 прилегало бы, кроме упомянутых выше треугольников, еще по одному треугольнику (рис. 26). Вся эта фигура, состоящая из шестиугольника S и пояса прилегающих треугольников, была бы треугольником С1С2С3 (рис. 26). В каждой вершине этого треугольника сходилось бы по четыре треугольника сети, сумма углов которых при этой вершине была бы меньше 180°, что противоречит сделанному в начале замечанию.
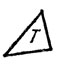
Рис. 23
Рис. 24
Рис. 25
Рис. 26
Противоречие приводит к выводу, что сети, описанной в задаче, не существует.
20. Пусть ОА0=а, ОВ0=b (рис. 27). По условию задачи b=aq, где
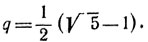
Сторона первого из отсеченных квадратов равна aq, сторона второго равна aq2, сторона третьего равна aq3, и т. д.
Пусть ОАn=хn, АnВn=yn (n = 1,2, , ..). Отрезки OA1=x1, ОA3=x3, ОА5=х5, . . . образуют возрастающую последовательность, а отрезки ОА2=х2, ОA4=x4, OA6=x6,.... образуют убывающую последовательность; обе эти последовательности сходятся к одному и тому же пределу, являющемуся абсциссой х некоторой точки А. Так как OA1=aq, A1A3=aq5, A3A5=aq9,... то
x=lim2n+1=aq+aq5+aq9+....=aq/(1-q4)
Аналогично отрезки y1=A1B1, y9=A3B3, y5=A5B5, ... образуют убывающую последовательность, а отрезки y3=А2В2, y4=А4B4, y6=A6B6, . . . образуют возрастающую последовательность; обе эти последовательности сходятся к одному и тому же пределу, являющемуся ординатой у точки А. Мы имеем
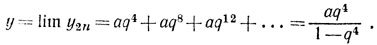
Из прямоугольника останется точка А с
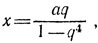
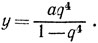
Она лежит на пересечении взаимно перпендикулярных A0B0 и A1C.
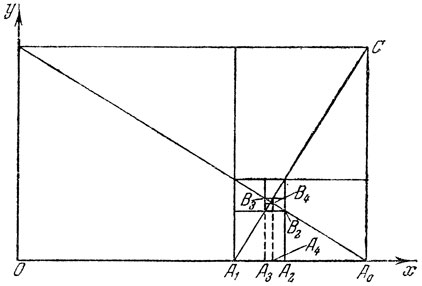
Рис. 27
20а. Меньший четырехугольник (рис. 28) является параллелограммом, так как его стороны попарно параллельны диагоналям первоначального четырехугольника. Эти диагонали делят большой четырехугольник на четыре треугольника, а малый - на четыре параллелограмма. Каждый из этих параллелограммов имеет площадь вполовину меньшую площади соответствующего треугольника, следовательно, площадь меньшего четырехугольника равна половине площади большого четырехугольника. Это же имеет место и в не выпуклом четырехугольнике (рис. 29), однако доказательство в этом случае отличается тем, что сложение площадей соответствующих треугольников или параллелограммов заменится вычитанием площадей.
Рис. 28
Рис. 29
21. Начертим квадрат 5 со стороной 1. Если два противоположных угла принадлежат одной и той же части, то это разбиение, очевидно, обладает нужным свойством, так как диагональ 5 равна √2, т. е. больше √65/64.
Пусть теперь каждые две противоположные вершины квадрата принадлежат разным его частям. Рассмотрим два случая:
1° существует часть, не содержащая вершин S;
2° каждый кусок квадрата содержит одну или две его вершины.
Рис. 30 относится к случаю 1°, с рассмотрения которого мы .и начнем. Обозначим кусок, содержащий вершины А1 и A2, через Α, а кусок, содержащий вершины В1 и В2 - через Β; последняя часть квадрата, вовсе не содержащая его вершин, пусть будет %. Вертикальные отрезки A1N, А2М имеют ДЛИНЫ 1/4 и 1/2 соответственно. Если М принадлежит части Α (если М∈Α), то мы берем Р=М, Q=A1 и получаем PQ= √5/4>√65/64, т. е. снова получаем подтверждение требуемого свойства разбиений квадрата. Если то мы полагаем Р=М, Q=B1 и получаем PQ=√5/4>√65/64, как и выше. Если N∈Α, мы полагаем P=N, Q=A2, в результате чего имеем PQ=√17/16>√65/64; если N∈Β, мы берем P=N, Q=B2 и получаем PQ=5/4>√65/64. Если же ни М, ни N не принадлежат частям Α, Β, то обе эти точки обязательно принадлежат части но тогда мы можем принять Р=М, Q=N, что дает PQ=√17/16>√65/64.
Перейдем теперь к случаю 2° - ему соответствует рис. 31. Обозначим часть квадрата, содержащую вершины А1 и А2, через Α, часть, содержащую вершину В - через Β и часть, содержащую вершину С,- через C. Середина М основания ВС квадрата 5 может принадлежать Α, Β или C. Если М лежит в Α, мы берем Р=М, Q=A1 и получаем PQ=√5/4. ЕСЛИ М∈Β, то рассмотрим точку N, лежащую на левой стороне квадрата 5 на расстоянии 1/8 от А1. Могут иметь место три , возможности:
(1) N∈Α, (2)N∈Β, (3)N∈C.
Мы полагаем P=N вне зависимости от того, в какой части находится N, но
выбираем Q=A2 в случае (1) и получаем PQ=√65/64,
выбираем Q=M в случае (2) и получаем PQ=√65/64,
выбираем Q=C в случае (3) и получаем PQ=√113/64>√65/64.
Если, наконец, M∈C, то мы выберем на правой стороне квадрата S на расстоянии 1/8 от правой верхней вершины точку N' и дальше поступим, как и в случае М∈Β наклонные линии на рис. 31 могут быть заменены другими такими линиями, выходящими не из N, а из N' Рассуждения здесь, по существу, не будут отличаться от использованных выше, только части 33 и % квадрата поменяются ролями.
Этим самым мы полностью доказали требуемое утверждение. Исследуем теперь вопрос о том, можно ли усилить утверждение задачи, Заменив число √65/64≈1,008 на большее (например, на 1,01). Ответ на этот вопрос является отрицательным, что .можно доказать следующим примером. Разобьем единичный квадрат на 3 равновеликие части Α, Β, C, как показано на рис. 32. Трапеции 33 и конгруэнтны и их общие стороны имеют длину 11/24. Длина каждого вертикального отрезка, являющегося стороной пятиугольника, равна 1/8. Рис. 32 нужно понимать следующим образом: внутренняя часть пятиугольника принадлежит Α, внутренняя часть левой трапеции принадлежит Β, правой трапеции - C. Все точки сторон пятиугольника, за исключением C1∈C целиком принадлежат Α. Стороны левой трапеции принадлежат Β, кроме стороны A3A4, которая, по условию, принадлежит Α. Стороны правой трапеции принадлежат C кроме A4C1 и короткой вертикальной стороны A4B2 длины 11/24, которая вся (за исключением точки А4∈Α) принадлежит Β. Легко видеть, что большая диагональ всех рассматриваемых многоугольников равна √65/64. Отсюда следует, что невозможно найти пару точек Р, Q, принадлежащих одной части разбиения, расстояние между которыми превышало бы √65/64. Отмеченный пунктиром отрезок A3A2 имеет длину, равную √65/64, его концы принадлежат Α. Заметим, что это - единственная пара точек, обладающая свойством, указанным в условии задачи*.
* (Относительно намеченной в этой задаче проблематики см., на? пример, Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Геометрические оценки и задачи из комбинаторной геометрии,- Мл Наука, 1974, цикл задач 5 Примеч. ред.)
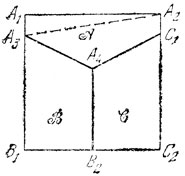
Рис. 32
22. Обозначение узлов сети способом, указанным в условии задачи, невозможно.
Для доказательства предположим обратное, т. е. что узлы сети можно обозначить так, как этого требует условие задачи, и рассмотрим произвольную строку сети. В этой строке обязательно имеются три следующие друг за другом узла, в которых выступят три различные буквы, например буквы а, b, с (в противном случае строка могла бы содержать самое большее две разные буквы, что противоречит условию задачи). В последующей строке (см. середину рис. 33), ниже узлов, обозначенных буквами а, b, с, должны находиться узлы, соответственно обозначенные буквами с, d, а, если обозначение узлов отвечает условию задачи. Тогда узлы следующей строки должны быть соответственно отмечены буквами а, b, с (правая часть, рис. 33).
Продолжая это рассуждение, мы видим, что в каждом из трех столбцов рассматриваемого участка сети выступают только две различные буквы: в первом выступают только буквы а, с, во втором - буквы b, d, в третьем - буквы с, а.
Итак, в узлах каждой строки и каждого столбца не могут выступать четыре различные буквы, и следовательно, не существует такого обозначения сети, о котором идет речь в задаче.
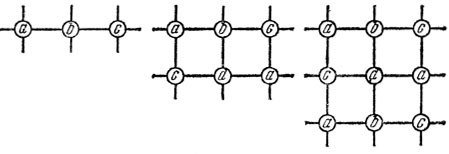
Рис. 33
23. Если на окружности радиусом r с центром в точке (√2, √3) расположены две точки (х, у) и (w, v) нашей решетки, то
(x-√2)2+(y-√3)2=(u-√2)2+(v-√3)2(=r2)
откуда
с√2+d√3=u2+v2-x2-y2=n
где с=2(u-x), d=2(v-y) и n - целые числа.
Следовательно,
2с2+3d2+2cd√6=n2,
Но поскольку √6 - иррациональное число, а с, d - целые числа, то предположение о том, что cd≠0, приводит к противоречию (в этом случаев√6=(n2-2c2-3d2)/2cd рационально), поэтому cd=0. Если с=0, то d√3=n, что может иметь место лишь при d=n=0; аналогично, d=0 дает с=0. Следовательно, c=d=0, т. е. х=u, ЧТО и означает совпадение точек (х, y) и (u, v).
24. Определение целочисленной решетки дано в условии задачи 22.
Для любого r обозначим через f(r) число точек решетки, находящихся внутри (не на границе!) круга радиусом r с центром в точке (√2, √3). Из предыдущей задачи следует, что при возрастании r число f(r) увеличивается единичными скачками. Мы покажем, что для достаточно малых r имеем f(r)=0, а для больших r величина f(r) принимает произвольно большие значения, Очевидно, что для r=0,1 имеем f(r)=0. Любой квадрат со сторонами, параллельными осям координат, длина которых больше натурального числа n, содержит по крайней мере n2 точек решетки, потому что между прямыми х=а и х=а+n имеется по крайней мере n перпендикулярных рядов точек решетки и между прямыми y=b и y=b+n тоже заключено по крайней, мере n горизонтальных рядов точек решетки. Но круг радиусом r>n содержит квадрат со сторонами, большими n (и параллельными осям координат), и, следовательно, он содержит по крайней мере n2 точек решетки, т. е. f(r)>n2 при r=n+1. Таким образом, мы выяснили, что f(r) - неограниченная функция, возрастающая от значения 0 единичными скачками, а следовательно, она принимает все целые положительные значения.
25. Ошибка заключается в том, что среднее арифметическое элементов бесконечной последовательности зависит от порядка рассматриваемых чисел (например, среднее чисел последовательности 1, 0, 1, 0, 1,0, . . . равно 1/2, а среднее тех же чисел, но упорядоченных следующим образом:
1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1,.....
равно 0). Ложное равенство 14=15 вытекает именно из использования различных способов упорядочения бесконечной последовательности, элементами которой являются углы семиугольников, заполняющих плоскость.
26. Предположим, что для n точек, из которых никакие три не лежат на одной прямой, можно найти замкнутый n-угольник, вершинами которого являются эти точки; пусть n+1 точек расположено так, что никакие три из них не лежат на одной прямой. Среди этих точек есть одна, например, точка P, которую можно отделить прямой от остальных точек. Пусть Wn - многоугольник, который согласно принятому предположению удовлетворяет условиям задачи и вершинами которого являются точки, отделенные от точки Р.
Ответ на поставленный в задаче вопрос будет утвердительным, если мы покажем, что по крайней мере одна из сторон многоугольника Wn целиком видна из точки Я, ибо тогда, заменяя эту сторону двумя отрезками, соединяющими точку Р с концами этой стороны, мы получим многоугольник Wn+1, отвечающий условиям задачи. Выберем какую-либо из сторон многоугольника Wn, например сторону А/А/+± (рис. 34). Если эта сторона полностью не видна из точки Я, т. е. если ее полностью или частично заслоняет другая сторона многоугольника Wn, то через сторону AiAi+1 проведем прямую и удалим все те стороны многоугольника, которые эта прямая полностью отделяет от точки Я. После этой операции число не удаленных сторон уменьшится по крайней мере на 1 (а именно на сторону АiАi+1). Эту же операцию проделаем с остальными сторонами многоугольника, снова выбирая одну сторону произвольно.
Рис. 34
Рис. 35
Рис. 36
Самое большее после n-кратного повторения такой операции на последней прямой будет лежать сторона, целиком видимая из точки Я. Устраняя эту сторону и соединяя ее концы с точкой Я, мы получим искомый (я+1)-угольник.
Так как утверждение задачи является очевидным для случая n=3, то положительный ответ на вопрос, поставленный. в задаче, можно считать доказанным.
27. Проведем окружность соответственно через точки 1,2,3 и 1,2,4. Если точка 4 лежит внутри окружности 12 3 или точка 3 лежит внутри окружности 12 4, то ответ на поставленный в задаче вопрос будет положительным. Допустим поэтому, что ни одна из этих возможностей не имеет места. Легко заметить, что тогда дуга окружности 12 3, лежащая вне окружности 12 4 делится на три части 13', 3'3" и 3"2 (рис. 35) такие, что если точка 3 лежит на 13', то точка 1 лежит внутри окружности 2 3 4, если 3 лежит на 3"2, то 2 лежит внутри 13 4, и если 3 лежит на 3'3", то имеют место оба эти явления.
Заметим еще, что одна (рис. 36) или две из трех названных выше частей дуги 1 2 могут исчезнуть. Однако всегда ответ на поставленный в задаче вопрос будет положительным.
28. Искомую кривую получаем, рассекая эллипс на четыре части и складывая их так, как показано на рис. 37.
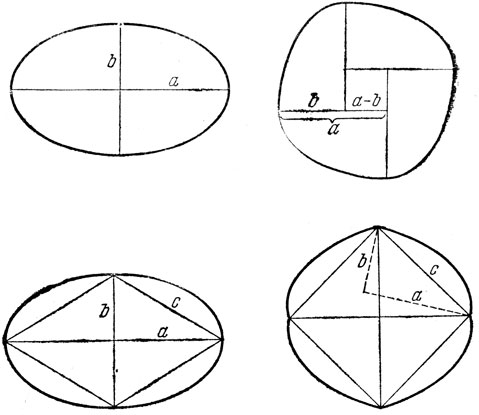
Рис. 38
А вот еще другое решение, не требующее "переворачивания" частей, т. е. выхода из плоскости эллипса. Соединяя поочередно вершины эллипса хордами (рис. 38), получаем ромб, окруженный четырьмя сегментами эллипса. Заменяем этот ромб, площадь которого равна 2ab, квадратом, площадь которого равна с2=а2+b2, так, чтобы четыре сегмента эллипса по-прежнему прилегали к сторонам квадрата. Площадь, ограниченная кривой, увеличивается на разность площадей квадрата и ромба, т. е. на
с2-2ab=a2+b2-2ab=(а-b)2.
29. Вместо всего пространства будем делить шар, через центр которого проводим плоскости. На поверхности шара (на ограничивающей его сфере) возникнут взаимно пересекающиеся большие окружности. Примем одну из них за экватор и все эти окружности спроектируем из центра шара на плоскость, касательную к шару в полюсе. Проекциями наших окружностей (за исключением одной, являющейся экватором и вовсе ни во что не проектирующейся) будут прямые. Следовательно, нужно вычислить максимальное число областей плоскости, разделенной n-1 прямыми. Методом индукции легко получить, что оно равно 1 + 1 + 2 + 3+...+(n-1)=1+1/2n(n-1), ибо при k-1 существующих прямых k-я прямая может увеличить число областей Самое большее на k. Так как на сфере имеется вдвое больше областей, чем на ее плоской проекции, то искомое число будет вдвое больше вычисленного нами выше, следовательно, оно равно n(n-1)+2. В частности, при n=4 искомым числом является 14.
30. Легко проверить, что преобразование, о котором идет речь в задаче, есть инверсия*. Действительно, пусть Π1 и Π2 касательные плоскости к земному шару соответственно в точках N и S (рис. 39). Пусть согласно определенному в задаче преобразованию, точка P1 на плоскости П1 и точка Р2 на плоскости П2 соответствуют друг другу.
* (См., например, Г ильберт Д., Кон-Фоссен С. Наглядная геометрия.- М.: Наука, 1984, § 36; Радемахер Г., Теплиц О. Числа и фигуры,-М.: Наука, 1966, тема 18.- Примеч. ред)
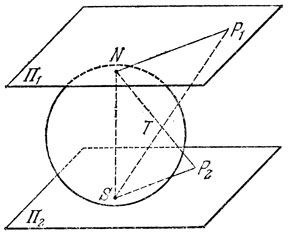
Рис. 39
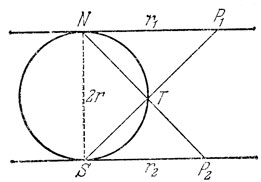
Рис. 40
Рассмотрим сечение земного шара и плоскостей П1 и П2 плоскостью, проведенной через ось NS (рис. 40). Обозначив NP1=r1, SP2=r2, NS=2r из подобия прямоугольных треугольников NTP1, STN, P2TS получим равенство r1r2=4r2, определяющее инверсию; если "поднять" плоскость Π2 совместив ее с Π1, то точки Р1 и Р2 будут лежать на одной прямой с центром N≡S инверсии и NP1×NP2=4r2= const.
31. Пряжа, наматываемая на куб, вращающийся вокруг одной из осей (рис. 41), удержится только на тех ребрах, которые не имеют общих точек с осью вращения; пряжа закрасит половину каждой грани куба, т. е. половину поверхности куба.
Теперь станем поочередно вращать куб вокруг каждой из четырех осей, каждый раз наматывая пряжу иного цвета.
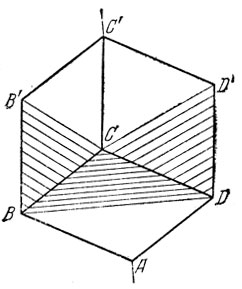
Рис. 41
Так, при вращении вокруг оси АС' используем пряжу цвета а (черного), при вращении вокруг оси DB' - пряжу цвета b (красного), при вращении вокруг оси BD' - пряжу цвета с (желтого) и, наконец? при вращении вокруг оси С А' используем пряжу цвета d (голубого).
Куб окажется закрашенным так, как это показано на рис. 42, на котором каждая грань разделена на четыре треугольника; буквы, размещенные в соответствующих треугольниках, обозначают цвета пряжи, покрывающей этот треугольник.
Легко заметить, что:
1° на поверхности куба. выступит шесть оттенков, т. е. столько, сколько существует комбинаций из четырех элементов по два, а именно: ab, ас у ad у bey bd и cd\
2° на каждой грани будет четыре разных оттенка;
3° поверхность куба будет покрыта двумя слоями пряжи;
4° противоположные грани куба будут окрашены в те же самые оттенки, расположенные в обратном циклическом порядке.
32. Докажем, что через каждую точку поверхности куба проходят четыре различные геодезические, всего же мы имеем семь семейств геодезических линий.
Если предположим, что куб гладкий, то резинка, обвитая вокруг него, уложится таким образом, что периметр созданного ею многоугольника достигнет минимума.
Три рода таких положений, а следовательно, три семейства таких геодезических, приведены на рис. 43; они лежат на плоскостях, параллельных граням куба. Чтобы убедиться, что возможны еще другие семейства геодезических, рассечем куб плоскостью, параллельной диагонали основания (рис. 44). Тогда, используя обозначения, указанные на рис. 44, будем иметь
х+y=a,
PK=a√2-2 xtg α ' KL = x√(1+2 tg2 α),
MN = a√2-2ytgα, LM = y√(1+2tg2α),
и для периметра p шестиугольника KLMNOP получим
p = 2a√2-2a tg α + 2a√(1+ 2tg2 α).
Следовательно, периметр p зависит только от угла а и во всех параллельных плоскостях_остается таким же; периметр этот достигает минимума, если tg α=1/√2. Стороны шестиугольника KLMNOP будут параллельны диагоналям граней куба и этот шестиугольник представляет собой геодезическую. Имеются четыре семейства таких геодезических, как это указано на рис. 45, а следовательно, вместе с предыдущими тремя всего семь семейств.
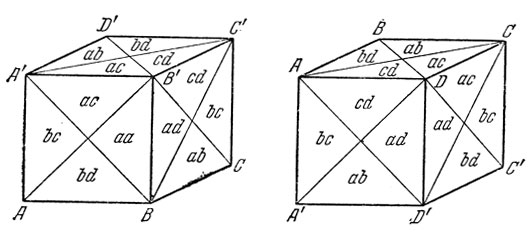
Рис. 42
Рис. 43
Рис. 44
Рис. 45
33. Взгляните на расположение шести кубов, представленное на рис. 46. Мы считаем, что куб В возник из А путем отражения от их общей грани, так же С из В, D из С, Е из D, F из Е. Вместо того, чтобы рассматривать движение частицы в кубе А согласно законам отражения, мы можем исследовать движение частицы в системе кубов A, ..., F по прямой линии. Если движение должно проходить по замкнутому шестиугольнику, то точка на передней грани А, с которой частица начала свой путь, в результате названных выше отражений должна совпасть с точкой на задней грани F. Если отрезок проведен так, как показано на рис. 47, то он пройдет все кубы А, . . ., F и не выйдет из них. "Стягивая" кубы в один, т. е. отражая куб F в грани, отделяющей F от Е, куб Е в грани, отделяющей Е от D, и т. д., мы получим в качестве пути движения шестиугольник, показанный на рис. 48.
Рис. 46
Рис. 47
Рис. 48
34. Все существующие развертки (которых всего 11) мы приводим на рис. 49. Шесть первых решений дают те развертки, в которых четыре грани куба расположены в одной полосе развертки. Других решений этого типа не существует, Последующие четыре развертки - это те, в которых есть три грани в одной полосе, но нет четырех граней. И, наконец, в последнем решении ни в одной полосе нет трех граней.

Рис. 49
35. Тела, образованные путем отсечения восьми углов куба, имеют 14 граней (количество граней куба + количество вершин куба). Восемь из них - треугольники, шесть - восьмиугольники (рис, 50).
Рис. 50
Рис. 51
При наибольших возможных октаэдрах грани четырнадцатигранника будут треугольниками и квадратами (рис. 51). Так как октаэдр возникает из куба путем отсечения восьми тетраэдров (треугольных пирамид) с основанием, равным 1/8 стороны куба, и высотой, равной половине стороны куба, то тетраэдры займут 8×1/3×1/8×1/2=1/6 часть пространства. В каждой вершине сходятся шесть тел: четыре четырнадцатигранника и два октаэдра (восьмигранника).
36. Нетрудно заметить, что ответ на вопрос, поставленный в задаче, будет положительным: гексаэдром, отвечающим условию задачи, является параллелепипед, у которого равны ребра и равны три плоских угла при одной из вершин.
Предположим, что дан ромб с острым углом а и диагоналями 2а и 2b. Складывая три таких ромба вершинами острых углов, получим трехгранный угол. Как этот угол, так и его ортогональная проекция на плоскость (вид с вершины) показана на рис. 52. Два сложенных вместе угла образуют гексаэдр, о котором говорится в задаче.
Заметим, что если α<60°, т# е. если b=a ctg α/2 > a√3, то гексаэдр можно построить только описанным^выше способом. Если же α>60°, если a<b<a√3 или а>b/√3, то из трех ромбов можно составить трехгранный угол не только складывая их вершинами острых углов, но также вершинами тупых углов 180-α (рис. 53). В этом случае, кроме гексаэдра рис. 52, мы получим удовлетворяющий условию задачи гексаэдр, изображенный на рис. 53.
Рис.52
Рис.53
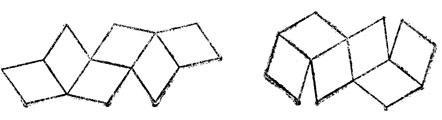
Рис.54
Если α=90°, то а-b и оба гексаэдра являются одинаковыми телами, а именно кубами.
На рис. 54 мы видим развертки обоих гексаэдров, рассмотренный 1 в задаче.
Стоит еще заметить, что гексаэдры, изображенные на рис, 52 и 53, представляют собой пример двух различных выпуклых многогранников с одинаковым числом попарно конгруэнтных граней.
37. Ответ зависит от того, считаем ли мы различными или нет два тетраэдра, получающихся друг из друга зеркальным отражением. Мы покажем, что в первом случае существует 60 различных тетраэдров! во втором случае число их, очевидно, сократится до 30.
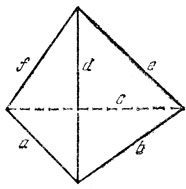
Рис. 55
Рассмотрим рис. 55, на котором изображен тетраэдр с ребрами, обозначенными буквами а, b, с, d, e, f Пронумеруем стержни, из которых мы собрали тетраэдр, числами от 1 до 6; стержень может использоваться в качестве каждого из ребер a, b, с, d, е, f. Следовательно, можно составить 6!=720 тетраэдров, правда, некоторые из них будут отличаться друг от друга лишь положением в пространстве.
Временно предположим, что изображенный на рис. 55 тетраэдр является правильным. Выясним, сколькими способами этот тетраэдр можно совместить сам с собою, перемещая его в пространстве. Ясно,' что расположение тетраэдра вполне определено тем, 1° какая из четырех граней тетраэдра переходит в основание и 2° какое из трех ребер этой грани совмещается с одним фиксированным ребром основания, например, с ребром а. Следовательно, существуют всего 3*4=12 различных положений тетраэдра,
Поэтому 720 возможных перестановок наших стержней, взятых в качестве ребер а-f, образуют каждый тетраэдр 12 раз, и, значит, существуют 720:12=60 различных тетраэдров, которые могут быть собраны из шести различных стержней. Если отождествить тетраэдры, получающиеся друг из друга зеркальным отражением, то различных тетраэдров будет вдвое меньше, т. е. 60:2=30.
38. Возьмем два треугольника со сторонами а, b, с и наложим один на другой так, чтобы с была их общей стороной (рис. 56). Раздвигая плоскости этих треугольников (рис. 57), мы увеличиваем расстояние между вершинами С1 и С2 (рис. 57) вплоть до максимального расстояния при треугольниках, снова лежащих в одной плоскости, но с противоположных сторон от А В (рис. 58).
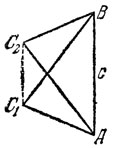
Рис.56
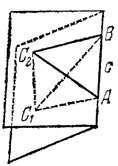
Рис.57
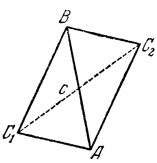
Рис.58
Обозначим расстояние С1С2 на рис. 56 через d1, то же самое расстояние на рис. 58 через d2. Условием существования тетраэдра, отвечающего условию задачи, является, следовательно, неравенство
d1<c<d2
Для того чтобы имело место неравенство d1<c, необходимо и достаточно, чтобы каждый из углов А к В был острый, а для того чтобы выполнялось неравенство c<d2, необходимо и достаточно, чтобы угол С был острый. Поэтому для существования тетраэдра необходимо и достаточно, чтобы треугольник АВС был остроугольным
Предположим, что так и есть. На рис. 59 мы имеем развертку тетраэдра, отвечающего условию задачи, причем
A1B1||AB, b1C1||BC, С1A1||AC.
Пусть
ВС=а, СА=b, АВ=с, a≤b≤c, 2р=а+b+с.
Сохраняя обозначения, используемые на рис. 59 и 60 замечаем, что высоту h=SO тетраэдра мы можем вычислить из прямоугольного SH1O сначала вычислив SH1=A1H1, и Н1О. Действительно
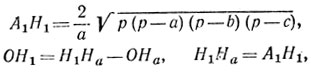
ОН1 = Н1На-ОНа, Н1На = А1H1
а ОНа мы можем вычислить из пропорции
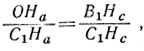
вытекающей из подобия треугольников С1ОНа и С1D1H1. Простое вычисление дает
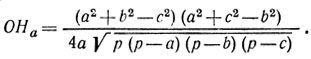
Мы имеем теперь
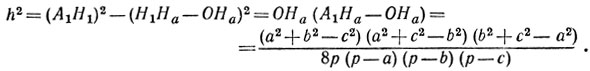
И, наконец, обозначая объем тетраэдра через и, получаем
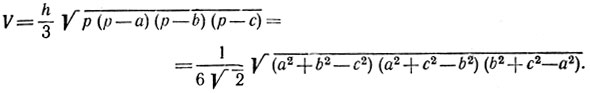
39. 2n-гранник, отвечающий условиям задачи, существует, и нетрудно указать способ его построения. С этой целью представим себе два параллельных круглых диска T1 и T2 одинаковых радиусов, центры которых O1 и О2 лежат на общем перпендикуляре к плоскостям дисков T1 и Т2 (рис. 61). Разделим окружность каждого диска на n≥3 одинаковых частей, пусть точки Р1, Р2,..., Рn и точки Q1, Q2 ,...., Qn обозначают соответственно точки деления окружностей дисков T1 и T2. Повернем диск Т1 в его плоскости так, чтобы ортогональная проекция точки Рk на плоскость диска T2 совпала с центром дуги QkQk+1 (проекция точки Рn - с центром дуги QnQ1).
Рис. 61
Рис. 62
На продолжениях отрезка O1O2 отложим отрезки O1S1 и O2S2 одинаковой длины h (рис. 61).
Затем соединим отрезком точку S1 с каждой из точек РK, а также точку S2 с каждой из точек Qk. Подобным же образом соединим каждую точку Pk с точками Qk, Qk+1. Таким образом возникает остов 4n-гранника, часть которого представлена на рис. 61.
Докажем, что размеры этого многогранника можно подобрать таким образом, чтобы он представлял собой 2n-гранник с конгруэнтными
Действительно, пусть длина отрезка O1O2 равна g. Рассмотрим четырехугольник S1P1Q2P2. Пусть M означает середин, отрезка P1P2. Для того чтобы названный выше многогранник был 2n-гранником с конгруэнтными гранями, необходимо и достаточно, чтобы отрезок S1Q2 пересекал отрезок Р1Р2 в точке М. Это условие будет выполнено, если будет иметь место равенство
откуда
Пои n=4 получим октаэдр, требуемый в задаче.
Можно доказать, что гранями 2n-гранника, отвечающего условию задачи, являются конгруэнтные дельтоиды, которые будут ромбами только при n=3(см. задачу 36).
40. В качестве требуемого тетраэдра рассмотрим пирамиду, основанием которой служит равносторонний треугольник АВС а боковые грани являются равнобедренными треугольниками АВЕ, ВСТ и САТ углами при вершинах Т, равными 30°. Изобразим на плоскости развертку пирамиды, получаемую, если разрезать пирамиду по ребру CT(рис 62) Рассмотрим точку М - середину ребра АВ и вершину пирамиды Т. Среди всех линий, соединяющих точки М и T, отрезок МT имеет наименьшую длину - это непосредственно следует из того, что МТ есть отрезок прямой не только на развертке, но и в пространстве, а все остальные соединяющие М и T линии будут отличны от отрезки прямой. Поскольку этот отрезок лежит на поверхности пирамиды то измеренное по поверхности расстояние между точками М и T равно длине этого отрезка. Однако мы еще должны показать, что точка T - самая дальняя от М точка поверхности :пирамиды На рис.62 ΔТС'B равносторонний и, следовательно, ∠TC'В равен 60° , a ∠TC'М>60°. Так как ∠С'ТМ=45°, то он меньше ∠TC'М и, следовательно, TМ>С'М Отсюда следует, что если точка S движется вдоль ребра С'T, то длина отрезка MS при его изменении от отрезка МС до отрезка МГ все время увеличивается. Это показывает, что любая точка S ребра С'Т находится на меньшем расстоянии от точки М, чем вершина T. Если теперь Q-произвольная точка треугольника С'TМ, то длина отрезка MQ меньше длины отрезка MS, где S - точка пересечения прямой MQ с ребром пирамиды С Г. Следовательно, расстояние от М до Q по поверхности пирамиды тем более меньше длины МI.
Очевидно, что в треугольнике С'МЛ точка С дальше всего удалена от точки М, а в треугольнике MAC такой точкой является С; остается заметить, что длины отрезков С'М и МС меньше длины МТ Так как кроме того, развертка симметрична относительно прямой то доказано, что точка Т дальше всех остальных точек пирамиды отстоит от точки М.
Мы предлагаем читателю, который хочет понять эту задачу до тетраэдр думать почему мы не взяли в качестве примера правильный
41. Многогранник образует пространственную сеть, сторонами которой являются ребра, узлами - вершины, а ячейками - грани многогранника. Дорога мухи должна образовать замкнутую ломаную линию, без кратных точек, принадлежащую указанной выше сети Возможность выделения такой дороги сохранится, мы деформируем сеть так, чтобы уместить ее на плоскости.
На рис. 63 мы видим растянутую на плоскости сеть ребер правильного додекаэдра. Жирной линией обозначен путь мухи, отвечающий условию задачи.
Теперь подобным же образом растянем на плоскости сеть ромбического додекаэдра (рис. 64). Узлы сети можно разделить на два класса: на такие, в которых сходятся четыре ребра (на рисунке последние обозначены черными точками).
Каждый узел первого класса соединен отрезком только с узлами второго класса, и наоборот. Поэтому муха во время своего путешествия должна была проводить поочередно через узлы первого класса и узлы первого класса и узлы второго. Так как узлов первого класса восемь, а узлов второго класса шесть, то муха не может посетить все вершины ромбического додекаэдра, передвигаясь по ребрам так, чтобы не пройти через одну вершину дважды и вернуться к исходной точке.
Рис. 63
Рис. 64
42. Расположим правильный додекаэдр так, чтобы иметь одну его грань Р прямо перед собой; будем ее называть передней гранью. Параллельную ей грань (невидимую нами) будем называть задней гранью. Совокупность пяти видимых граней, окружающих переднюю грань, назовем кольцом I, а совокупность пяти невидимых граней, окружающих заднюю грань, назовем кольцом II.
Так как в задаче речь идет об определении числа способов окраски граней додекаэдра, то мы можем додекаэдр заменить плоским его изображением, как показано на рис. 65 (задней грани Т соответствует часть плоскости, лежащая вне большого пятиугольника), или еще более простым плоским изображением, воспроизведенным на рис. 66.
Рис.65
Рис.66
Правильный додекаэдр нельзя выкрасить в три цвета так, чтобы смежные грани всегда отличались окраской. В самом деле, если бы, например, передняя грань была цвета A, то пять граней кольца I, смежных с передней гранью, следовало бы выкрасить двумя цветами - В и С, что невозможно.
Предположим теперь, что грани додекаэдра можно выкрасить в четыре цвета А, В, С, D требуемым в задаче способом. Легко заметить, что тогда каждый из этих цветов выступал бы три раза. Чтобы это обосновать, предположим обратное: что какой-то цвет, например A, выступает менее чем три раза, тогда иной цвет, например В, выступал бы более чем три раза. Предположим, например, что передняя грань выкрашена в цвет В. Тогда в кольце I цвет В не мог бы выступить, вследствие чего из шести невидимых граней по крайней мере три должны были бы быть цвета В. Однако это невозможно, ибо если бы задняя грань была цвета В, то в кольце II цвет В вообще не мог бы выступить, а если бы задняя стена не была цвета В, то в кольце II цвет В мог бы выступить самое большее два раза.
Из приведенного выше рассуждения следует также, что задняя грань не может быть такого же цвета, как передняя, но должна быть такого цвета, который в кольце I выступает два раза.
Наконец, заметим, что, устанавливая цвета кольца I, очередность, в которой эти цвета не выступают, а также цвет задней грани, мы одновременно однозначно устанавливаем способ окраски всего двенадцатигранника. Действительно, например, в случае, представленном на рис. 67, передняя грань должна быть цвета A. Что же касается граней кольца II, то грань 1 не может быть иного цвета, кроме A; в этом случае грань 2 будет цвета D, грань 5 - цвета В, вследствие чего грани 3 и 4 будут соответственно цвета В и A. Рассмотренный нами пример подтверждает, что окраска додекаэдра в четыре цвета возможна.
Рис.67
Предположим, что передняя грань додекаэдра, раскрашенного в четыре цвета, будет цвета A. Тогда в кольце I могут выступить шесть различных расположений цветов, так как при каждом расположении цветов задняя грань может быть выкрашена двумя различными способами; всего существует 12 возможных размещений цветов, как это видно из рис. 68. Но так как в додекаэдре, выкрашенном в четыре цвета, грань цвета A выступает только три раза, то при выборе какого-либо способа окраски из числа показанных на рис. 68 мы можем путем вращения додекаэдра исчерпать самое большее еще два способа окраски, т. е. всего три способа. Из этого следует, что способов окраски додекаэдра существует самое меньшее четыре.
Рис.68
Рис.69
Рис.70
Легко можно убедиться, что существуют в точности четыре способа окраски.
Действительно, при каждом из способов окраски, показанных в первой строке рис. 68, будут исчерпаны те способы, которые изображены в том же самом столбце.
42а. На рис. 69 представлена фотография модели додекаэдра с вписанным кубом; рис. 70 представляет параллельную проекцию этого додекаэдра с вписанным кубом.
Куб можно вписать в додекаэдр пятью различными способами*. На рис, 71 изображен один и тот же куб (тот, который изображен и на рис. 70) и четыре других, пронизывающих его куба, вписанных в додекаэдр.
* (С существованием этих пяти кубов тесно связана невозможность решения в радикалах общего уравнения 5-й степени, на чем мы, однако никак не можем здесь остановиться. [По поводу связи учения о разрешимости в радикалах алгебраических уравнений с теорией правильных многогранников см., например, Клейн Ф. Элементарная математик с точки зрения высшей, т. I.-М.; Л.: ОНТИ, 1935, с. 190-237.- При* меч. ред.] )
Рис.71
Рис. 72 представляет осевое сечение додекаэдра с вписанными в него кубами; сечение тела, образованного всеми кубами, показано на рисунке жирной линией. Исходя из этого рисунка, можно легко составить развертку или рисунок тела, образованного всеми кубами; им будет звездчатый 360-гранник. Основным элементом этого тела является пятилучевая звезда, образованная из ребер кубов (рис. 73). Такая звезда соответствует каждой грани додекаэдра; следовательно, всего их будет 12. Каждая из них имеет в центре пятигранное углубление, окруженное пятью трехгранными углублениями. Каждая звезда окружена пятью четырехгранными углублениями, посредством которых она соединяется с пятью соседними звездами (на рис. 73 показано только по две грани каждого из четырехгранных углублений).
Рис. 74 изображает прямоугольную проекцию тела, образованного всеми кубами со стороны граней описанного додекаэдра. На нем видна данной башенки. Видны также три дальнейшие звезды, прилегающие к предыдущим звездочкам.
Рис.72
Рис.73
Наконец, на рис. 76 изображена прямоугольная проекция тела, видного со стороны грани одного из кубов, т. е. со стороны четырехгранного центральная звезда, окруженная венцом пяти соседних звезд, воспроизведенных на рисунке в искаженном виде. Острия звезд по три сходятся в вершинах описанного додекаэдра и образуют 30 двенадцатигранная башенок, Башенки эти окружены равносторонними треугольниками, образованными ребрами кубов. На рис. 75 показано тело в прямоугольной проекции, видимое со стороны башенки, т. е. со стороны вершины описанного додекаэдра. На рисунке видны три звезды, сходящиеся у углубления, соединяющего соседние звезды тела, или со стороны ребра додекаэдра.
Рис.74
Чтобы вычислить объем тела, легче всего начать с вычисления площадей всех частей, на которые делит грань додекаэдра звезда, изображенная на рис. 73, а затем, используя рис. 72, вычислить расстояния от грани додекаэдра до вершин углублений звезды рис. 73. Это даст возможность вычислить объемы пирамид, которые необходимо вычесть из объема додекаэдра, чтобы получить объем звездчатого тела.
Рис.75
Рис.76
Если через а обозначим ребро додекаэдра, а через
- радиус описанной вокруг его грани окружности, то подсчет даст нам следующие значения соответственно для площадей оснований и высот пирамид:
для каждого из трехгранных углублений
для пятигранного углубления
для половины каждого из четырехгранных углублений
Поэтому, чтобы вычислить объем V звездчатого тела, следует из объема додекаэдра
вычесть двенадцати кратную сумму объемов перечисленных выше пирамид, т. е. 12×1/3(5S1h1 + S2h2 + 5S3h3), откуда, наконец, следует, что
Остается установить, какое тело образует общая часть всех кубов. Снова воспользовавшись осевым сечением додекаэдра с вписанными кубами (рис. 77, на котором жирной линией обозначено сечение рассматриваемого нами сейчас тела), приходим к выводу, что общая часть всех кубов является ромбоидальным тридцатигранником, изображенным в параллельной проекции на рис. 78. Длина отрезка АВ является длиной большей диагонали, а длина отрезка АС - длиной меньшей диагонали ромба. На рис. 79-81 изображен тот же тридцатигранник в прямоугольной проекции: со стороны пятигранного угла (ось аа' на рис. 77), со стороны трехгранного угла (ось bb' на рис. 77) и со стороны грани (ось сс на рис. 77).
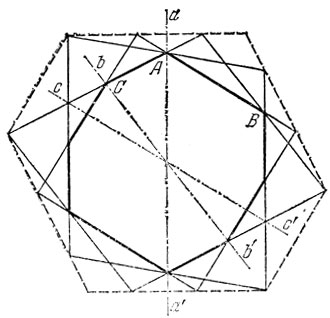
Рис.77
Рис.78
Рис.79
Рис.80
Рис.81
43. Возьмем произвольный выпуклый многогранник. Одну из его граней примем за основание пирамиды с настолько малыми двугранными углами при основании, чтобы многогранник, полученный из выпуклого многогранника путем пристройки к нему этой пирамиды, был выпуклым и чтобы можно было в первоначальном многограннике сделать углубление, симметричное этой пирамиде относительно избранной грани. Таким образом получим два многогранника: выпуклый и не выпуклый, с гранями выпуклыми и попарно конгруэнтными. На рис. 82 показаны два многогранника ABCDE и ABCDE', полученных описанным выше способом из тетраэдра ABCD.
Два тридцатигранника: выпуклый и не выпуклый, с выпуклыми попарно конгруэнтными гранями изображены на рис. 83 и 84.
Рис.82
Рис.83
Рис.84
44. Примеры многогранников, удовлетворяющих условиям задачи, мы видим на рис. 85 и 86. Многогранник, изображенный на рис. 86, состоит из двух параллелепипедов с ромбоидальными гранями, прилегающих друг к другу одной гранью.
Рис.85
Рис.86
Рис.87
Существует также не выпуклый ромбический додекаэдр. Мы можем его получить из выпуклого ромбического додекаэдра, если удалим передний трехгранный угол (см. рис. 87, а) и заменим его задним трехгранным углом, передвигая его параллельно по ребра, образованным шестью остальными гранями (см. рис. 87, б).
Видно, что возникшее тело состоит из трех параллелепипедов. Если мы удалим один из них, то у нас останется тело, изображенное на рис. 86, 44а. Отыскание всех многоугольников, образованных ребрами правильного многогранника, способом, описанным в задаче, а особенно отыскание тех из многоугольников, которые отличаются только положением, а не формой,- особенно затруднительно в случае икосаэдра. Поэтому установим некоторый метод решения, заменяя многогранники плоскими схематическими изображениями их разверток (рис. 88). Это даст нам возможность рассматривать данную задачу как задачу плоскую.
Соответствующее плоское изображение развертки мы можем получить, если представим себе, что ребра многогранника - растягивающиеся, и станем растягивать многогранник, начав, например, с "задней" грани, так, чтобы все вершины многогранника оказались в одной плоскости. Вершинам многогранника соответствуют узлы плоской сети, ребрам соответствуют отрезки или дуги, соединяющие узлы, а каждой грани многогранника соответствует либо отдельная ячейка сети, либо внешняя область. Обходу по ребрам многогранника соответствует обход по сторонам и дугам плоской сети, а замкнутому косому (неплоскому) многоугольнику, соединяющему все вершины правильного многогранника, соответствует замкнутая ломаная, не имеющая узлов и проходящая через все узлы плоской сети. Эта ломаная имеет столько сторон, сколько вершин у данного правильного многогранника, причем "сторонами" мы считаем также дуги (впрочем, это зависит лишь от рисунка, ибо плоские изображения можно нарисовать так, чтобы они состояли из одних отрезков).
Рис. 88
Чтобы можно было различать косые многоугольники, образованные способом, описанным в задаче, установим некоторую систему их обозначения, приписывая им некоторые символы. А именно: представим себе пловца, который плывет по ребру АВ многогранника лицом к многограннику. Доплыв до вершины В пловец имеет возможность выбрать количество дорог, равное уменьшенному на единицу числу ребер, выходящих из одной вершины данного многогранника. Будем обозначать эти дороги в той последовательности, в которой они следуют одна за другой по направлению вращения часовой стрелки, соответственно цифрами 0,1 для правильного тетраэдра, куба и додекаэдра, цифрами 0, 1,2 - для правильного октаэдра и цифрами 0, 1,2,3 - для правильного икосаэдра. Таким образом, каждому замкнутому косому многоугольнику, проходящему через все вершины многогранника, будет соответствовать символ, составленный из такого числа цифр, сколько вершин имеет многогранник. Так, например, многоугольники рис. 89 соответственно будут обозначаться символами 00110011 и 11001100, если обход их начнем от вершины А по направлению, обозначенному стрелкой.
Заметим, что совершенно безразлично, с которой цифры мы начнем прочитывание символа многоугольника, лишь бы мы после последней цифры прочли еще пропущенные начальные цифры. Действительно, началу прочитывания символа многоугольника с другой цифры соответствует начало обхода многогранника с иной вершины. Поэтому два многоугольника рис. 89 идентичны, хотя и по-разному расположены.
Заметим, далее, что если дан символ многоугольника, то легко можно написать символ многоугольника, полученного из данного путем зеркального отражения (т. е. путем симметрии относительно плоскости). Для этого достаточно заменить цифры 0,1 соответственно цифрами 1, 0, если символ составлен из цифр 0, 1, или заменить цифры 0, 2 соответственно цифрами 2, 0 (оставляя цифру 1 без изменения), если символ составлен из цифр 0, 1,2, или же заменить цифры 0, 1,2, 3 соответственно цифрами 3, 2, 1,0, если символ составлен из цифр 0, 1,2, 3. Так, например, из двух многоугольников, представленных на рис. 89, каждый возникает из другого путем симметричного отражения, что следует из сравнения их символов.
Рис. 89
Рис.90
Наконец, заметим, что каждый многоугольник можно обойти в двух противоположных направлениях. Обходя многоугольник рис. 90, начиная с вершины А, по направлению А В, а затем, начиная с вершины В, по направлению ВА, мы соответственно получим символы 201201 и 120120. Второй из этих символов можно получить из первого, прочитывая его в обратном-порядке, при такой замене цифр, которая соответствует симметричному отражению.
В случае, представленном на рис. 90, оба символа, которые обозначают ту же самую замкнутую ломаную, проходимую в двух противоположных направлениях, в сущности, являются идентичными, ибо второй символ, прочитываемый со второй цифры, дает то же самое, что и первый. Однако не всегда так бывает. Например, замкнутая ломаная рис. 91, обегаемая от А к В, имеет символ 102302301132, а та же самая ломаная, проходимая от В к А, имеет символ 102230130132. Эти символы не являются идентичными, хотя линии, представленные ими, отличаются лишь направлением обхода.
Нетрудно объяснить этот факт. Если пловец плывет лицом к додекаэдру вдоль ломаной (см. рис. 91) в направлении АВ, то по правую руку он будет иметь те грани додекаэдра, которые на рисунке находятся внутри замкнутой ломаной. Плывя же вдоль этой ломаной в противоположном направлении, он будет иметь по правую руку то, что останется от додекаэдра после удаления из него тех граней, которые составляют внутренность ломаной, изображенной на рис. 91. Итак, введенный нами символ характеризует не только саму ломаную, но и часть многогранника, принимаемую за ее внутренность. Поэтому, если данная ломаная делит поверхность многогранника на две одинаковые части (как в примере, показанном на рис. 90), то символ ломаной не меняется при изменении направления обхода. В противном же случае (как на рис. 91) изменение направления обхода вызывает изменение символа ломаной. Таким образом отождествлении многоугольников необходимо помнить, что один и тот же многоугольник может иметь два разных символа.
После этих предварительных замечаний, которые облегчат нам перечисление идентификацию многоугольников, отличающихся только положением, а не формой, мы можем перейти к решению задачи, поочередно рассматривая различные правильные многогранники.
Начнем с правильного тетраэдра, имеющего четыре грани. Многоугольник, о котором идет речь в задаче, имеет, следовательно, четыре стороны. Такому многоугольнику соответствует четырехзначный символ, записанный при помощи цифр 0 и 1. В этом символе, однако, не могут выступать подряд ни две цифры 0, ни две цифры 1, так как они вызывают замыкание треугольника (рис. 92). Ввиду этого в символе многоугольника должны выступать попеременно цифры 0 и 1. Единственным многоугольником с таким символом является многоугольник 0101, так как символ 1010 обозначает тот же самый многоугольник.
Следовательно, в случае тетраэдра задача имеет только одно решение (рис. 93); при этом можно проверить, что, симметрично преобразовывая многоугольник 0101 или обегая его в противоположном направлении, мы всегда получаем тот же самый многоугольник.
Рис.91
Рис.92
Рис.93
Рис.94
Рис.95
Рис.96
В случае куба (восемь вершин) многоугольником, отвечающим условию задачи, будет восьмиугольник с восьмизначным символом. В этом символе не могут выступать подряд ни три цифры 0, ни три цифры 1 (ибо это вызывает замыкание четырехугольника, см. рис. 94). В связи с этим в символе многоугольника, отвечающего условию задачи, должны выступать как цифры 0, так и цифры 1. А так как многоугольник 01010101 не реализует условия задачи (рис. 95), то в символе каждого многоугольника, отвечающего условию задачи, должны выступать подряд или две цифры 0, или две цифры 1. Заменяя в этом последнем случае многоугольник симметричным ему многоугольником, мы можем ограничиться перечислением многоугольников, проходящих через ребро АВ, символы которых начинаются двумя цифрами 0. Остальные многоугольники (если они существуют) мы получим путем симметричного отражения.
Рис.97
Рис.98
Рис.99
Однако существует только один многоугольник, отвечающий этим условиям, а именно многоугольник 00110011 (рис. 96). А так как зеркальное отражение даст нам тот же самый многоугольник 11001100, то и в этом случае задача имеет только одно решение (рис. 97). Нетрудно проверить, что, обегая многоугольник 00110011 в противоположном направлении, мы получим тот же самый многоугольник, т. е. замкнутая ломаная рис. 97 делит поверхность куба на конгруэнтные части.
Перейдем теперь к правильному октаэдру (рис. 98). Замкнутая ломаная, отвечающая условиям задачи, состоит из шести сторон, т. е. она имеет шестизначный символ, составленный из цифр 0, 1,2. Так как в таком символе не могут выступать подряд три цифры 1 (ибо это вызывает замыкание четырехугольника), то каждый символ шестиугольника, отвечающего условию задачи, содержит по крайней мере одну из цифр: 0 или 2. Заменяя в последнем случае шестиугольник симметричным шестиугольником, мы видим, что для решения задачи достаточно перечислить шестиугольники, проходящие, например, через ребро АВ, символы которых начинаются с цифры 0. Существуют три таких шестиугольника (рис. 99) с символами
[1] 012012, [2] 020202, [3] 021021.
Преобразовывая их симметрично, получим шестиугольники
210210, 202020, 201201,
совпадающие соответственно с шестиугольниками [3], [2] и [1]. Отсюда следует, что при преобразовании симметрии первый шестиугольник переходит в третий, третий - в первый, а второй переходит сам в себя.
Поэтому для правильного октаэдра задача имеет три решения: одно симметричное 020202 и два ассимметричных: 012012, 021021 (рис. 100).
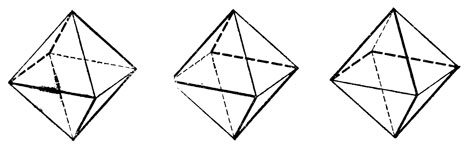
Рис. 100
Обегая каждую из полученных замкнутых ломаных в обратном направлении, получим те же самые символы; это означает, что каждая из указанных замкнутых ломаных делит поверхность октаэдра на конгруэнтные числа.
Для правильного додекаэдра (рис. 101) многоугольник, отвечающий условию задачи, состоит из двадцати сторон и имеет двадцатизначный символ, составленный из цифр 0 и 1. Так как многоугольник
01010101010101010101
не отвечает условию задачи (рис. 102), то в символе каждого многоугольника, отвечающего условию задачи, выступают подряд по крайней мере две цифры 0 ил и две цифры 1. Заменяя в последнем случае многоугольник симметрично отраженным многоугольником, мы ограничимся перечислением многоугольников, проходящих через ребро АВ, символы которых вначале имеют две цифры 0. Остальные многоугольники (если они существуют) мы получим путем симметричного отражения.
Рис. 101
Рис.102
Исследуя поочередно все возможные случаи, мы можем легко убедиться, что существуют четыре многоугольника, проходящих через ребро АВ, символы которых начинаются двумя цифрами 0 (рис. 103). Это многоугольники
[1] 00010101110001010111 [2] 00011101010001110101,
[3] 00101011100010101110, [4] 00111010100011101010.
Многоугольники [1], [3] идентичны; кроме того, идентичны многоугольники [2], [4], а многоугольник [2] получается из многоугольника [1] в результате зеркального отражения. Каждый из многоугольников [1], [2], обегаемый в обратном направлении, дает тот же самый символ. Отсюда следует, что для правильного додекаэдра задача имеет два асимметричных и взаимно симметричных решения; каждая из полученных замкнутых ломаных делит поверхность додекаэдра на две конгруэнтные части (рис. 104).
Самым трудным является случай правильного икосаэдра (рис. 105). В этом случае многоугольник" отвечающий условию задачи, должен быть двенадцатиугольником, символ которого построен из двенадцати цифр 0, 1,2, 3. Пусть дан многоугольник W с символом, например,
102123102123, (W)
удовлетворяющий условиям задачи. Обозначим буквой S многоугольник, образованный из многоугольника W путем симметричного отражения. Символ многоугольника 5 получаем заменяя цифры 0, 1, 2, 3 соответственно цифрами 3, 2, 1, 0:
231210231210, (S)
Рис.103
Рис. 104
Рис. 105
Затем обозначим буквой (S') символ многоугольника S, обегаемого в противоположном направлении; символ (S') получаем, прочитывая в обратном порядке символ (W):
321201321201. (S')
Обозначим, наконец, буквой (IF) символ многоугольника W, обегаемого в противоположном направлении; символ (IF) получаем, прочитывая в обратном порядке символ (S):
012132012132. (W')
Можно легко убедиться, что в символе произвольного многоугольника, удовлетворяющего условию задачи, не могут подряд выступать ни две цифры 0, ни две цифры 3 (ибо это вызывает замыкание треугольника). А так как многоугольник 030303030303 не отвечает условиям задачи (см. рис. 105), то, следовательно, в символе каждого многоугольника, отвечающего условиям задачи, выступает по крайней мере один раз цифра 1 или же цифра 2. Заменяя во втором случае многоугольник W симметричным многоугольником S, мы можем ограничиться перечислением таких многоугольников, символы которых содержат цифру 1. Остальные многоугольники (если они существуют) получаем путем симметричного отражения. Докажем теперь, что если символ многоугольника, отвечающего условиям задачи, содержит цифру 1, то он содержит также и группу (комплекс) цифр 10 или 01, или же комплекс цифр 23 или 32 (а тогда символ симметричного многоугольника содержит комплекс цифр 10 или же 01).
Действительно, если цифра 1 не выступает в комплексе цифр 10 или 01, то обязательно выступит в одном из комплексов 111, 112, 113, 212, 213,313 или в одном из комплексов, полученных из предшествующих путем прочтения их в обратном порядке. Заменяя в последнем случае многоугольник W многоугольником S', мы можем ограничиться исследованием первого случая.
Комплекс 111 не может выступить, если многоугольник W отвечает условию задачи, ибо вершина е не могла бы тогда принадлежать многоугольнику W (рис. 106).
В том случае, когда выступит комплекс 112 (или 113), должно существовать соединение fej (рис. 107), которому соответствовала бы цифра 0 в вершине j и цифра 1 в вершине а, т. е. комплекс цифр 01 в символе - многоугольника.
Рис. 106
Рис.107
В случае, когда выступит комплекс 212 (или 213), должно существовать соединение cbe (рис. 108). -Если бы вершина е соединялась с вершиной f, то ломаной febc в символе многоугольника соответствовал бы комплекс 10. А если бы вершина е соединялась с вершиной j, то ломаной beja в символе многоугольника соответствовал бы комплекс цифр 10.
И, наконец, если бы выступил комплекс 313, то должно было бы выступить также соединение bid (рис. 109). Вершины j, k не могут соединяться ни непосредственно между собой, ни с вершиной fr вследствие чего должно выступить соединение je или kg. Ограничиваясь из-за симметрии рассмотрением" первого случая, мы видим, что тогда возможны три следующих соединения вершин е, b: или eb, или ecb, или efcb. В случае соединения eb ломаной beja в символе многоугольника W соответствует комплекс цифр 10, а в случае соединения ecb или efcb ломаной dibc в символе многоугольника соответствует комплекс цифр 32.
Рис. 108
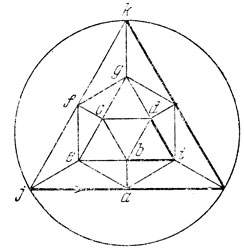
Рис. 109
Таким образом, мы констатируем, что если только в символе многоугольника выступает цифра 1, то выступает также и комплекс цифр 10 либо 01, или 23 либо 32. Поэтому заменяя в случае надобности многоугольник W многоугольником S и беря соответственно вместо символов (S) и (W),символы (S') и (W'), мы можем ограничиться перечислением таких многоугольников, которые проходят через определенное произвольно выбранное ребро и символы которых начинаются с комплекса цифр 10. Остальные многоугольники (если они существуют) получим путем симметричного' отражения.
Существуют два метода перечисления описанных выше многоугольников. Один, аналогичный тому, который мы применяли для додекаэдра, основан на исследовании всех возможных рисунков. Другой состоит в комбинировании сначала трех, а потом шести вершин, через которые могут проходить рассматриваемые многоугольники. Каждый из этих методов (детали опускаем) ведет к следующим многоугольникам:


Теперь остается отбросить из числа приведенных выше многоугольников те, которые идентичны другим, и дописать многоугольники, полученные путем симметричного отражения и отличные от предыдущих.

Сразу видно, что многоугольник [25] идентичен многоугольнику (12], что обозначим символически равенством [25]=[ 12], и подобным же образом: [31]=[21], [33]= [15], [36]=[28], [38]=[13], [39]=[7], [40]=[27].
Отбросив многоугольники [25], [31], [33], [36], [38], [39], [40], мы займемся остальными, которых всего [34]. Их символы выписаны в таблицу.
Из этой таблицы видно, что многоугольники [9], [28], [23], [35], [24], [37] соответственно идентичны многоугольникам [4], [34], [6], [7], [12], [13], и что, симметрично преобразуя многоугольники [3], [26], [27], [32], [41], получаем новые многоугольники, отличные от рассмотренных выше,
В результате, для икосаэдра задача имеет 33 решения, а именно: один симметричный многоугольник [14] и 16 многоугольников [1], [2], [3], [4], [5], [6], [7], [8], [10], [11], [12], [13], [26], [27], [32], [41], симметричных 16 многоугольникам: [17], [16], [42], [34], [21], [30], [29], [15], [22], [20], [19], [18], [43], [44], [45], [46].
Из них многоугольники [2], [16], [3], [42], [8], [15], [10], [22], [26], [43], [27], [44], [41], [46] делят поверхность икосаэдра на конгруэнтные части.
На рис. ПО показано решение [14], на рис. 111 приведены 16 остальных решений из столбца (W) предыдущей таблицы; симметричных решений мы не помещаем. Обход мы начинаем с нижней вершины, а поочередные решения на рис. 111 расположены вдоль строк.
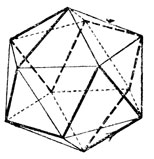
Рис. 110
Рис. 111
45. Три модели конусообразных планет, о которых шла речь в условии задачи, мы получаем из прямоугольной сети меридианов и параллелей (рис. 112), рассекая ее одним из трех способов, указанных на рис. 113, и сворачивая затем остальную часть в конус с вершиной в точке N,
На рис. 114 дан вид этого конуса "сверху", т. е. со стороны вершины. Мы ясно различаем два семейства кривых: "меридианы" и "параллели".
Меридианы не пересекают друг друга, параллели тоже, но каждый меридиан пересекает каждую параллель в двух точках, как и на земном шаре. Кратчайшие пути имеют постоянное направление, т. е. пересекают параллели и меридианы под постоянным углом.
На рис. 115 и 116 дан вид "сверху" второго и третьего конусов, или проекции семейств кривых на плоскости, перпендикулярные к оси конуса. На первом конусе имеется одно семейство кривых, на другом - три.
Стоит заметить, что приведенные решения не единственны.
46. Среди трех данных сфер нет двух, касающихся друг друга. В самом деле, в противном случае общая касательная плоскость этих двух сфер, проходящая через точку Р, пересечет третью сферу по окружности. Касательная к этой окружности в точке Р будет, очевидно, касательной ко всем трем сферам, что противоречит условию задачи.
Итак, две сферы должны пересекаться по окружности, проходящей, очевидно, через точку Р. Эта окружность не может иметь с третьей сферой только одну общую точку, так как иначе касательная к окружности в точке Р была бы общей касательной к трем сферам. Точка пересечения этой окружности с третьей сферой, отличная от точки Р, принадлежит всем трем сферам.

Рис. 112
Рис. 113
Рис. 114
Рис. 115
47. Пусть окружность К является сечением нашей поверхности S, и пусть L - ось окружности К у т. е. прямая, проходящая через центр К перпендикулярно ее плоскости. Рассмотрим плоскость Р, проходящую через L; она высекает на S окружность, которую мы обозначим через С (Р), Очевидно, С(Р) пересекает К в двух диаметрально противоположных точках А и В. Ясно, что А В является хордой окружности С(Р), а ось L будет осью симметрии этой хорды. Как известно, ось симметрии хорды окружности проходит через центр этой окружности; поэтому L проходит через центр С (Я) и пересекает эту окружность в диаметрально противоположных ее точках М и N, (которые., разумеется, суть точки пересечения L и S). Следовательно, любая окружность С (Р), получающаяся в сечении поверхности 5 произвольной плоскостью Р, проходящей через прямую L, содержит одни и те же точки М и N. Очевидно, не существует других точек L, принадлежащих 5, так как если Q - такая точка, то сечение S плоскостью Р будет отлично от окружности.
Рис. 116
Отсюда мы заключаем,что отрезок MN прямой L является общим диаметром всех окружностей С(Р). Поэтому все эти окружности могут быть получены вращением вокруг MN любой из них. Таким образом, множество всех сечений S плоскостями, проходящими через L, дает нам сферу ∑, являющуюся частью поверхности S. Но S не может содержать никаких точек, отличных от точек Σ, потому что если некоторая точка Т поверхности S не принадлежит Σ, то пересечение S плоскостью, проходящей через Т и L, будет отлично от окружности. Следовательно, поверхность S - это сфера 2.
47а. Если уложить вместе четыре шара радиусом r, то их центры образуют правильный тетраэдр с ребром 2r (левая часть рис. 117), в котором двугранный угол α≈70°32', что нетрудно найти из равенства cos α = 1/3.
Если мы и дальше будем строить многогранники, образованные из центров шаров, то вкладыванию нового шара в какое-нибудь из оставшихся гнезд будет соответствовать достройка к ранее построенному тетраэдру нового тетраэдра, симметричного предыдущему относительно одной из его граней. Так как гнезд было всего четыре, то докладыванию четырех шаров соответствует достройка к тетраэдру четырех тетраэдров. В результате мы получим звездчатый многогранник, изображенный на правой части рис. 117. Они имеют 12 граней, а следовательно, фигура, состоящая из шаров, имеет 12 гнезд.
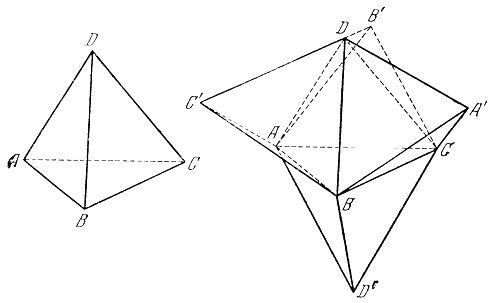
Рис. 117
Если бы мы теперь хотели в каждое из образованных гнезд вложить по одному шару, то оказалось бы, что не все шары вмещаются. Действительно, если, например, при грани А'ВС мы достроим тетраэдр A'BCD", а при грани BCD' - тетраэдр A"BCD', то действительно, это построение может быть выполнено, ибо 5α<360°, но расстояние A"D" между вершинами достроенных тетраэдров будет равно 2r√3 sin ( 180°-5/2α), т. е. 2/9r, а следовательно, будет меньше 2r. Поэтому точки А" и D" одновременно не могут быть центрами шаров с радиусом r.
Таким образом, из каждой пары гнезд при каждом из внутренних ребер звездчатого многогранника можно только в одно гнездо вложить новый шар, т. е. в качестве третьего слоя всего можно доложить только шесть шаров. Этот один шар можно действительно поместить, так как, например,
А'А" = 2r√3 sin 2α = 8√6/9r>3r
Постоянно говоря дальше "грань" вместо "гнездо" и "вершина" вместо "центр шара", предположим, что "активными" гранями являются грани A'BD, B'CD, CAD, ABD', BCD', ACD', а остальные пусть будут "мертвыми" (неактивными).
Тогда к данному многограннику можно будет достроить тетраэдры A'BDG, B'CDE, AC'DF, ABC"D, A"BCD', AB"CD', имеющие всего 18 граней. Три последних тетраэдра будут иметь только по одной активной грани. Подобным же образом каждый из трех начальных тетраэдров будет иметь только по одной активной грани, т. е. всего в четвертом слое будет 6 шаров.
Этот процесс, конечно, можно продолжить. После присоединения каждого последующего слоя шаров некоторые грани многогранников, образованные центрами шаров, будут "отмирать", но остальные активные грани будут порождать новые тетраэдры.
47б. Пусть к обозначает радиус данных шаров.
Прежде всего, заметим, что один шар мы можем обложить венцом из шести шаров так, чтобы каждый из них касался первого шара (который мы будем считать первым слоем) и двух соседних шаров и чтобы центры всех шаров лежали в одной плоскости (рис. 118). Углубления, образованные каждыми тремя взаимно касающимися шарами, из числа этих семи шаров, образуют 12 гнезд для последующих шаров; принимая плоскость, изображенную на рис. 118, за плоскость, проходящую через центры названных семи шаров, в гнездах, находящихся выше этой плоскости, мы можем поместить только три шара касательно к шару первого слоя. Шары эти, обозначенные на рис. 118 пунктиром, действительно можно уместить, так как легко убедиться в том, что расстояния между их центрами будут равны 2к. В гнездах, находящихся ниже плоскости, можно уместить тоже только три шара, причем двумя способами: не посредственно ниже шаров, находящихся в верхних гнездах, или же между ними.
Рис. 118
Итак, один шар можно двумя способами обложить 12 шарами, составляющими второй слой. Центры этих 12 шаров представляют собой вершины двух четырнадцатигранников W1 и W2 (рис. 119 и 120), шесть граней которых являются квадратами, а восемь граней - равносторонними треугольниками; стороны квадратов и треугольников равны 2r. Так как центры шаров второго слоя находятся на одинаковом расстоянии 2r от центра шара первого слоя, то и вершины четырнадцатигранников W1 и W2 тоже находятся на одинаковом расстоянии от центра шара первого слоя. Расстояние это равно 2r. Основываясь на этом, можно вычислить двугранные углы многогранников W1 и W2. В самом деле, соединяя вершины многогранников с центром шара первого слоя, мы можем выделить в обоих многогранниках шесть пирамид с квадратными основаниями и одинаковыми ребрами, равными 2r, а также восемь правильных тетраэдров с ребрами длиной 2r. Обозначая двугранный угол у основания пирамиды через α, а двугранный угол тетраэдра через β, легко найдем, что
cos α = 1/√3, cos β = 1/3,
откуда
α=54° 44', β=70°32".
Двугранные углы многогранника W1 поэтому равны α+β; двугранные углы многогранника W2 соответственно равны: между двумя треугольными гранями 2β, между двумя квадратными гранями 2а, а между треугольной и квадратной гранью α+β.
Рис. 119
Рис. 120
Обе системы шаров, центры которых являются вершинами четырнадцатигранников W1 и W2 содержат по 14 гнезд; восемь гнезд, образованных тремя шарами, шесть - четырьмя шарами. Легко убедиться, что в каждое гнездо можно уместить шары (как это доказать?). Следовательно, третий слой будет состоять из 14 шаров. Так как звездчатый многогранник W1 рис. 121 имеет 48 граней, то шары третьего слоя, центры которых составляют этот многогранник, образуют 48 гнезд. Ни в одно из них невозможно уже вместить шар (почему?).
Рассмотрим еще систему шаров, центрами которых являются вершины четырнадцатигранника W2, и звездчатый многогранник Wg2, построенный на многограннике W2. В этом случае в гнездах третьего слоя системы шаров можно поместить три шара, образующие четвертый слой, но на этом окончится, так же как и раньше, укладывание шаров в гнезда. Мы уже не сможем поместить пятого слоя шаров*.
* (По поводу затронутой задачами 47а и 476 тематики см., например, Гильберт Д., Кон - Фоссен С. Наглядная геометрия.- М.: Наука, 1981, § 7,- Примен. ред.)
47в. Решение иллюстрирует рис. 122, Наборщик набрал 5 см вместо указанных автором учебника 4 см,
48. Электрическое освещение в большинстве городов питается переменным, током с периодом, равным gg с; в течение секунды электрический свет 100 раз загорается и гаснет, а между двумя очередными моментами наивысшего напряжения всегда проходит 0,01 с.
Рис. 121
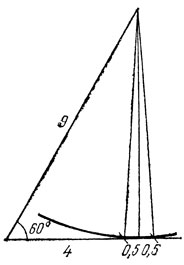
Рис. 122
Если диск вращается по направлению вращения часовой стрелки со скоростью 25 оборотов в секунду, то в течение 0,01 с каждый из участков внутреннего диска выполнит 0,25 оборота и займет такое положение, какое раньше занимал участок того же самого цвета. В результате нам будет казаться, что внутренний диск не вращается. При скорости вращения, несколько превышающей 25 оборотов в секунду, нам будет казаться, что диск соответственно вращается в направлении движения часовой стрелки, а при скорости вращения немного менее 25 оборотов в секунду нам будет казаться, что диск вращается в направлении, противоположном движению часовой стрелки.
Для внешнего кольца будет то же самое, однако критическая скорость будет равна 20 оборотам в секунду.
Предположим теперь, что мы станем вращать диск с очень большой скоростью. Если скорость, уменьшаясь, дойдет до 25 оборотов в секунду, то нам будет казаться, что внутренний диск неподвижен, а внешнее кольцо вращается по направлению движения часовой стрелки. При скорости диска менее 25, но более 20 оборотов в секунду нам будет казаться, что внутренний диск вращается в направлении, противоположном вращению внешнего кольца, При 20 оборотах в секунду внешнее кольцо задержится, после чего как внутренний диск, так и внешнее кольцо будут вращаться в направлении, противоположном направлению движения часовой стрелки.
Игрушка лучше всего действует при свете ионной лампы, а совсем плохо при свете обыкновенных электрических лампочек большой мощности, нить накала которых обладает большой тепловой инерцией, весьма сильно снижающей эффекты, связанные с характером переменного тока.
49. Спор можно разрешить следующим образом.
Право первенства выбора куска ветчины предоставим третьей участнице покупки. Она, конечно, выберет тот кусок, который на домашних весах весил не менее каждого из двух остальных кусков, а следовательно, тот, который, по ее мнению, по своей стоимости соответствует не менее чем 15 рублям. Такой кусок должен существовать, так как при разделе целого на три части одна из этих частей должна быть не менее 1/3 целого.
Затем выбирает свой кусок вторая участница покупки. И эта тоже должна быть довольна, так как после того, как выбрала себе кусок третья участница, остался по крайней мере один кусок, который, по показанию весов в магазине на углу, соответствует по своей стоимости не менее чем 15 рублям.
Первая участница покупки получит оставшийся кусок; она тоже должна быть довольна, ибо она считала все куски равными по весу.
50. Систему двух произвольных взаимно перпендикулярных прямых назовем кратко крестом. Отметим на этом кресте один луч, т. е. одну полупрямую (на рис. 123 он обозначен стрелкой). Крест, расположенный произвольно относительно плоской области, можно всегда параллельно сдвинуть так, чтобы четверти области, прилегающие к выделенному нами лучу, имели площади, равные Р/4 (на рис. 123 крест обозначен пунктиром; верхние четверти, имеющие площади Р/4, тоже заштрихованы пунктиром). Если и нижние четверти имеют те же самые площади, то теорема доказана.
Предположим,что это не так, т.е. что левая нижняя четверть имеет площадь больше Р/4 (и больше правой нижней четверти). Будем теперь вращать крест по часовой стрелке так, чтобы четверти, прилегающие к его отмеченному лучу, всегда имели площади, равные Р/4. После того как мы повернем крест на 90°, он займет положение, обозначенное на рис. 123 сплошной линией. Для того чтобы четверти, заштрихованные сплошной линией, имели площади, равные Р/4, вертикальный луч должен переместиться влево, а горизонтальный - вверх. При новом положении креста нижняя левая четверть (по отношению к выделенному лучу) имеет площадь меньше Р/4, так как является частью заштрихованной пунктиром четверти, имеющей площадь Р/4, а поэтому правая нижняя четверть имеет площадь больше Р/4. Следовательно, мы получили обратное тому, что было при первоначальном положении креста; поэтому при вращении креста обязательно найдется такое его положение, при котором все четверти будут иметь одинаковые площади, равные Р/4.
Рис. 123
(Представленное нами доказательство возможности раздела лепешки на четыре равные части обошлось без всяких вычислений. Но они были бы необходимы - причем достаточно сложны - при фактическом разделе на четыре части данного треугольника, например, со сторонами 3, 4, 5.)
51. Сначала заметим, что если Павел выберет точку Р в центре масс треугольника (рис. 124), то наилучшим для Гавла будет такой раздел торта, при котором сечение параллельно какой-либо из сторон треугольника. Для доказательства этого факта достаточно показать, что треугольник, заштрихованный один раз на рис. 124, имеет площадь меньшую, чем треугольник, заштрихованный дважды. Площадь части ABCD торта равна 5/9 площади целого торта, следовательно, торт будет поделен между Гавлом и Павлом в отношении 5 : 4.
Легко проверить, что выбор центра масс является для Павла наилучшим ибо при каждом ином положении точки Р, Гавел мог бы себе отрезать не только трапецию A BCD, но еще, сверх того, кусок торта (рис. 125).
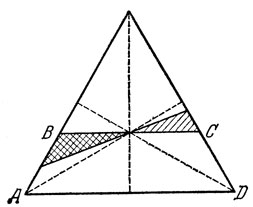
Рис.124
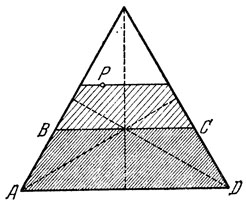
Рис. 125
Ответить на остальные вопросы мы предлагаем читателям. Во всяком случае легко доказать, что если торт имеет причудливую форму, представленную на рис. 126, то при любом выборе точки Р Гавел может отсечь по меньшей мере 2/3 торта. И наконец, мы предлагаем читателям доказать, используя результат задачи 50, что при любой форме торта Гавел не отрежет более чем 3/4 торта*.
* (По поводу связанной с этой задачей проблематики, см., например, первую часть книги Г рюнбаум Б. Этюды по комбинаторной геометрии и теории выпуклых тел,- М.: Наука, 1971.- Примеч. ред.)
Рис. 126
52. Сравним вначале по весу первую пару предметов, затем вторую пару, и, наконец,- предмет, который оказался - более тяжелым в первой паре, с более тяжелым предметом второй пары. Мы можем записать результаты этих взвешиваний как
(здесь M<N означает, что М легче N).
Пятый предмет Е может быть включен в ряд А - В - С для чего надо сравнить его сперва с В; если он окажется тяжелее мы сравним его с A. Таким способом, с помощью взвешиваний мы включим Е в последовательность А и L и придем к одной из следующих четырех конфигураций:
Мы сделали пока всего 5 взвешиваний. Если в результате мы пришли к 1 , сравним далее D с А, если окажется, что D<A, то задача реше на; если же окажется, что A<D, мы сравним D с В - это седьмое взвешивание завершит процесс, и мы получим A<D<B<C<E или А<В<D<C<E. Если первые 5 взвешиваний дадут 2°, то мы можем включить D ряд с помощью двух взвешиваний, начиная со сравнения D c B - всего мы используем опять 7 взвешиваний. Конфигурации 3° и 4 отличаются от 2 только обозначениями, так что здесь рассуждения, по существу, не отличаются от относящихся к случаю 2°
Следовательно, семи взвешиваний всегда достаточно для упорядочения пяти предметов.
52а. Из описания дороги путешественника следует, что его палатка стояла на Северном полюсе. В этом месте земного шара восход солнца бывает только раз в году - в день весеннего равноденствия т. е. 21 марта. Это и есть день рождения Невядомского.
53. Обозначим поочередно дни недели через I, II, . . ., VII и составим таблицу, условившись, что день недели, который выпал на некоторую определенную дату 1911 года, обозначен числом I.
В столбце A приведены годы (високосные годы напечатаны жирным шрифтом). В столбце В приведены дни недели, выпадающие в разные годы на ту же самую дату, что и в 1911 году, если эта дата находится между 1 января и 28 февраля. В столбце С приведены дни недели, выпадающие в различные годы на ту же самую дату, если эта дата находится между 1 марта и 31 декабря. В столбце D приведены дни недели, выпадающие в отдельные високосные годы на 29 февраля.
Из этой таблицы видно, что день недели, выпадающий на определенную дату до 1 марта, перемещается после обычного года на 1, а после високосного года на 2; день же недели, выпадающий на определенную дату после 1 марта, перемещается перед обычным годом на 1, а перед високосным годом на 2.
Из этой таблицы также видно, что если определенная дата (отличная от 29 февраля) выпадает в некотором году, например, в понедельник, то во второй раз в этот же самый день недели, она выпадает или через 5 лет, или через 6 лет, или же через 11 лет (если в рассматриваемый период не было года, номер которого является числом, делящимся на 100, но не делящимся на 400).
Если бы Софья Сергеевна родилась в какой-либо день, отличный от 29 февраля, а до 27 июля 1950 г. отмечала день своего рождения только один раз, то в этот день она была бы еще несовершеннолетней, следовательно, не было бы повода называть ее Софьей Сергеевной, а также говорить, что она еще не стара.
Предположим, следовательно, что Софья Сергеевна родилась 29 февраля. День недели, выпадающий на эту дату, перемещается через каждые четыре года на 5, вследствие чего 29 февраля выпадает в тот же самый день недели, через каждые 7*4=28 лет (если в этот период не было года, номер которого делится на 100, но не делится на 400). Так как Софье Сергеевне "всего один год", то первый день своего рождения она отмечала самое раннее в 1924 году, а самое позднее в 1948 году.
Но так как известно, что Софья Сергеевна родилась после первой мировой войны, то впервые день своего рождения она отмечала в 1948 году, а родилась 29 февраля 1920 года.
54. Пусть n обозначает число рыб в пруду, годных для улова. Тогда отношение числа рыб, помеченных меткой, к числу всех рыб равно 30/n.
Во второй раз ихтиолог поймал 40 рыб, среди которых две рыбы были помечены. Отношение числа рыб помеченных к числу всех выловленных рыб равно 1/20.
Если предположить, что помеченные рыбы в пруду равномерно распределены среди всех рыб, то оба отношения должны быть одинаковы, т. е. 30/n=1/20, откуда n=600.
Следовательно, число рыб в пруду, годных для улова данной сетью, приблизительно равно 600.
55. В любом случае достаточно четырех проб, если принять следующий метод: будем сравнивать валик со средним отверстием, т. е. восьмым по счету, потом - в зависимости от результата - с четвертым или двенадцатым и т. д. Результатом каждой пробы будет ответ "да" (если валик поместится в отверстии) или "нет" (если валик не поместится в отверстии). Четыре пробы дадут 16 возможностей, т. е. столько, сколько существует типов валиков, различаемых данным прибором.
56. Если 2n чисел x1, х2, . . ., х2n расположены в возрастающем порядке и если хm<x<xm+1, то сумма абсолютных погрешностей при замене чисел x1, х2, . . ., х2n числом х равна
(х - x1)+(х - х2)+...+(х - хm)+(хm+1 - х) +...+(х2n - x)(1)
Легко проверить, что самым меньшим из чисел вида (1) является число
(y-x1)+(y-x2)+...+(y-xn)+(xn+1-y)+...+(x2n-y) (2)
где xn<y<xn+1. Действительно, если, например, m>n (следовательно, x>y)у то разность чисел (1) и (2) равна
n(x-y) +((x-xn+1+..+(x-xm))-((xn+1-y)+...+(xm-y))+(2n-m)(y-x)>n(x-y)+0-(m-n)(x-y)+(2n-m)(y-x)=0
Подобным же образом можно проверить, что если систему 4n чисел х1, х2, ...., x4n разделим на две части:
х1, х2, ..., х2m и х2m+1,.....,x4n
числа первой части заменим числом х', причем таким, что хm<x'<xm+1 числа второй части заменим числом х", причем таким, что х2m<x"<x2n+m+1, то сумма абсолютных погрешностей будет наименьшей при m=n.
Отсюда следует, что предельный диаметр для 120 шариков равен 6,09 мм (имеется 60 шариков диаметром менее 6,09 мм и столько же шариков диаметром более 6,09 мм), а надписи на коробках следующие: а=6,06 мм, b=6,15 мм.
57. Площадь поперечного сечения валика равна 25π см2, лента заполняет площадь 25 см2, следовательно, сердцевина имеет площадь 25 (π-1) см2. Обозначим через d диаметр трубки (без ленты); тогда из уравнения
πd2)/4=25(π-1)
следует, что
d = 10√((π-1)/π) см ≈ 8,26 см.
58. Как известно, время, которое показывают часы, полностью определено координатой малой стрелки на шкале часов (рис. 127); большая стрелка имеет всего лишь вспомогательное значение, а именно, она создает на диске часов что-то вроде нониуса, что позволяет двенадцатикратно увеличить точность определения координаты малой стрелки.
Если координату малой стрелки на диске часов обозначим через а координату большой стрелки через ξ, то получим
η-12{ξ}=0, 0≤ξ<12, 0≤η<12
где {ξ} обозначает дробную часть числа ξ.
Предположим, что обе стрелки часов одинаковы. Обозначим через х координату одной стрелки, а через "/ - координату другой. Могут иметь место три случая.
I. Если х-12 {y}≠0, то обязательно
y-12{x}=0
и часы показывают время х.
II. Если y-12{х}≠0, то обязательно
x-12{y}=0
и часы показывают время y.
III. Если одновременно имеют место равенства
y-12{x}=0 и х-12{y}=0,
то при помощи часов с одинаковыми стрелками мы не можем прочесть время, ибо каждую из стрелок можно принять за малую стрелку, а следовательно, одинаково возможно время х и время у; таких исключительных положений стрелок существует всего 143.
Рис.127
Рис.128
Отвечающие им числа х и y являются координатами 143 точек пересечения графиков функций y=12{x} и х=12 {y} (рис. 128). Точки эти лежат, на 23 прямых, определенных уравнениями
y=x+12/13k, (k=0, ±1, ..., ±11) (1)
Если теперь обозначим через
r=|x-y|
ошибку, которую мы допустим, приняв вместо одного из двух показаний часов (х и y) другое, то согласно равенству (1) будем иметь
r=12/13|k|, (k=0, ±1,...,±11)
Отбрасывая, согласно условию задачи, ошибку более чем в 6 часов, мы получаем наибольшее значение ошибки для k=±6. Она равна r=72/12=5 7/13 , т. е. 5 ч 32 мин 18 6/13 с. (В какое время грозит нам эта
ошибка?) Конечно, в этом рассуждении мы предположили, что хозяин часов безошибочно прочитывает координаты стрелок.
59. 1) Могло случиться, что один и тот же мальчик оказался самым низким великаном и самым высоким карликом. Более того, класс, состоящий из km учеников разного роста (k и m - натуральные числа, большие 1; k обозначает число рядов, m обозначает число шеренг), можно расставить в прямоугольном строю таким образом, чтобы произвольно выбранный ученик w, который имеет по меньшей мере k - 1 товарищей ниже себя и по меньшей мере m - 1 товарищей выше себя, оказался одновременно самым низким великаном и самым высоким карликом:
2) Нет таких классов, в которых самый низкий великан меньше самого высокого карлика.
Чтобы это доказать обозначим через и самого высокого карлика, а через U - самого низкого великана, Предположим, что U<u. Ученики u и U не могут стоять ни в одном и том же ряду (так как тогда и не был бы самым низким в своем ряду), ни в одной и той же шеренге (так как тогда и не был бы самым большим в своей шеренге). Обозначим через uik ученика, стоящего в точке пересечения ряда и шеренги, в которых соответственно, стоят ученики и и U. Получим тогда
u<uik, uik<U
вследствие чего u<U, вопреки сделанному предположению, что U<u. Предположение, что U<u привело, следовательно, к противоречию и поэтому оно не верно.
3) Если бы учитель при определении великанов искал их так же, как и карликов, т. е. в рядах, а не в шеренгах, то один и тот же ученик не мог бы быть, что совершенно очевидно, самым низким великаном и самым высоким карликом, так как тогда в своем ряду он должен был бы быть одновременно самым низким и самым высоким учеником, что невозможно.
Однако в этом случае самый низкий великан может быть или больше или меньше самого высокого карлика.
Действительно, из класса, насчитывающего km учеников разного роста, выберем совершенно произвольно 2k+m-2 учеников и расставим их вдоль трех сторон прямоугольника по росту в убывающем порядке
u1, u2,..., u2k+m-2
следующим образом:
Оставшихся учеников расставим прямоугольным строем совершенно произвольно.
Ученик uk является самым низким великаном, ученик uk+m-1 является самым высоким карликом, а так как uk>uk+m-1 то самый низкий великан будет больше самого высокого карлика.
Если же k+2m-2 учеников u1, u2,..., расставим в убывающем порядке по росту так: а остальных учеников расставим в прямоугольном строю совершенно произвольно, то ученик будет самым низким великаном, а ученик um будет самым высоким карликом и вследствие неравенства uk+m+1<um самый низкий великан будет ниже самого высокого карлика.

60. Вопросы, поставленные в задаче, обозначим соответственно теми номерами, под которыми они выступают, и используем символ p→q (импликация) для обозначения того, что из ответа "да" на вопрос р следует ответ "да" на вопрос q. Тогда верны следующие импликации:
Итак, одинаковыми являются ответы на вопросы 2 и 4, а также 3 и 7.
61. Символы, о которых идет речь в задаче, следующие
Докажем, что среди этих 16 символов есть два, а именно abсd и a'bed', которыми нельзя обозначить поезда.
Пусть символ Рр обозначает число курящих путешественников в купе для курящих, Рn - число курящих путешественников в купе для некурящих, Nр - число некурящих путешественников в купе для курящих, a Nn - число некурящих путешественников в купе для некурящих.
Рассмотрим теперь символ ab'c'd. Соответственно смыслу букв а, b',t',d должны быть выполнены следующие неравенства:
Рр>Рп, Np<Nn, Рр<Nр, Рn>Nn. (1)
Из трех первых неравенств получаем
Nn>Nр>Рр>Рn,
следовательно, Nn>Pn, что противоречит четвертому из неравенств (1).
Символ ab'c'd - как противоречивый - не может служить для обозначения поезда.
Противоречивым является также символ abed , так как среди определяющих его неравенств
Рр<Рn, Np>Nn, Рр>Np, Рn<Nn
три первые противоречат четвертому.
Остальными четырнадцатью символами можно обозначить поезда, как это следует из приведенной ниже наглядной схемы:
62. Расположим символы, обозначающие группы крови, в одну строку и в один столбец: доноров поместим в столбец, а реципиентов - в строку, и полученную таблицу заполним знаками "+" и "-" следующим образом:
Эту таблицу нужно понимать так: выберем произвольную строку (например, 2-ю) и произвольный столбец (например, 3-й); если в их пересечении стоит знак + , то донор выбранной строки может дать свою кровь для переливания реципиенту, указанному в выбранном столбце; он не может этого сделать, если в пересечении строки и столбца стоит знак -. Так, в случае второй строки и третьего столбца мы получаем, что донор с группой крови А не может давать свою кровь человеку с группой крови В. Таким образом, таблица указывает, кто кому может и кто кому не может дать свою кровь.
в Легко проверить, что это определение удовлетворяет закону I. Действительно, этот закон сводится к тому, что на диагонали должны стоять только знаки +, что, очевидно, выполнено. Закон II требует, чтобы в строке донора О стояли только знаки +, это требование также удовлетворено. Закон III требует, чтобы в столбце реципиента А В стояли только знаки + , но это, очевидно, тоже верно. Если в отношениях I, II, III мы заменим X на символы О, А, В, А В, то получим ровно 9 отношений, а именно те, которые обозначены в нашей таблице знаком +.
Так как все остальные места в таблице (их число равно 7) заполнены знаками -, то, очевидно, закон IV тоже выполнен.
Итак, наша таблица эквивалентна законам I-IV, что и доказывает утверждение 1°. Утверждение 2° также может быть проверено с помощью таблицы. Например, 0→А и А→АВ, но также и 0→AB, что и подтверждается нашей таблицей. Для всех остальных случаев утверждение 2° может быть проверено таким же образом. Утверждение 3° вытекает из наличия знака - в соответствующей клетке таблицы.
63. Условимся обозначать через X также и человека с группой крови X. В частности, братьев мы обозначим символами X и Y. Так как X не может дать свою кровь Y, то в таблице, построенной в решении предыдущей задачи, на пересечении строки X со столбцом Y стоит знак -. Так как К не может дать свою кровь X, то на пересечении строки Y со столбцом X также стоит знак -. (Эти два минуса симметричны относительно диагонали таблицы, состоящей из одних лишь знаков +.) Но легко усмотреть, что пара симметрично расположенных относительно диагонали минусов находится только на пересечении строки А со столбцом В и строки В со столбцом А. Поэтому один из братьев имеет группу крови А, а другой - группу крови В. Таблица показывает, что А может получать кровь только от О и от А, В - только от О и от В. Так как оба брата могут получить кровь от своей матери, то она должна иметь группу крови О. Законы наследования групп крови требуют приписывания О к одно буквенным символам родителей, в соответствии с этим обозначим мать символом ОО.
Закон комбинирования букв, заимствованных из символов крови обоих родителей, показывает, что братья получили свои символы А и В от отца, так как их мать не обладает ими. Следовательно, их отец есть А В. Родители с символами А В и 00 могут иметь детей лишь с символами АО и ВО, т. е. А и В (в соответствии с законом вычеркивания О); следовательно, сестра этих братьев тоже относится к группе А или В. Значит, как показывает таблица, она может дать свою кровь одному и только одному из братьев. (Никто в этой семье не может брать кровь у отца, но каждый может взять кровь у матери.)
63а. Находящиеся в обращении монетные единицы для грошей, десятков грошей и злотых одинаковы и равны 1, 2 и 5. Таким образом, для решения задачи достаточно исследовать, сколько различных сумм наверняка содержит каждая сумма от 1 до 9 грошей. Результаты иллюстрирует следующая таблица:
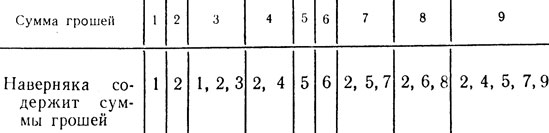
Пользуясь этой таблицей, мы можем вычислить, сколько различных сумм содержит наверняка данная сумма. Например, имея 527 грошей, можно выплатить любую сумму, которая на месте сотен будет иметь одну из цифр 0 или 5, на месте десятков будет иметь одну из цифр 0 или 2, на месте единиц будет иметь одну из цифр 0, 2, 5, 7. Всего различных сумм будет 2×2×4=16, а если мы не станем принимать в расчет сумму 000, то их будет 15.
Больше всего сумм наверняка содержит сумма в 999 грошей, а именно, 63-1=215 различных сумм.
Стоит заметить, что интересным свойством обладает число 6. Сумма в 6 грошей может быть составлена либо из монеты в 5 грошей и монеты в 1 грош, либо из трех монет по 2 гроша каждая. В первом случае мы не могли бы выплатить сумм в 2, 3, 4 гроша, а во втором случае не могли бы выплатить сумм ни в 1, ни в 5 грошей. Таким образом, имея 6 грошей, мы можем выплатить наверняка (в смысле, определенном в задаче) всего лишь одну сумму, а именно 6 грошей. Однако же, имея 6 грошей, мы безусловно можем выплатить по меньшей мере три различные суммы!
63б. Из условий задачи легко получить соотношения
s1 + s2 + ....+ sn = m
g1 + g2 + .....+ gm = n
Так как один и тот же сорт деревьев может расти в нескольких садах, а также в одном и том же саду может расти несколько сортов деревьев, то справедливы следующие соотношения:
1×s1 + 2×s2 +....+ n×sn ≥ n,
1×g1 + 2×g2 +....+ m×gm ≥ m,
64. Если столб M расположен между столбами L и N, то путь
АВС . . . LMN ... T
короче пути
АВС ... LN ...ТМ
на отрезок ТМ. Отсюда вывод: чтобы путь
АВС . . . LMN ... T
был самым длинным путем, необходимо, чтобы всегда два соседних отрезка этого пути имели противоположные направления. Тогда длина пути выразится следующей формулой:
d = А̄В̄ - В̄С̄ + D̄Ē +...
причем, если число столбов нечетное, то
d' = ĀB̄ - B̄C̄ + C̄D̄-D̄Ē + ... + R̄S̄ - S̄T̄
а если число столбов четное, то
d" = ĀB̄ - B̄C̄ + C̄D̄ - D̄Ē + ...- R̄S̄ + S̄T̄.
Обозначим через
x0, x1, x2,...,xn (1)
координаты столбов A, В, С, ..., Т. Вследствие сказанного выше, будет
x0<x1, x1>x2, x2<x3, x2>x4,....
Так как по условию задачи столбы расставлены на равных расстояниях, то можно считать, что последовательность (1) является некоторой перестановкой чисел 0, 1,2, .... n.
Тогда из равенств
ĀB̄ = x1-x0, B̄C̄ = x2-x1, C̄D̄ = x3-x2,....
x0+x1+x2+....+xn=n(n+1)/2
получаем
d' = n(n + 1) - 4(x2 + x4 + x6 +... + хn-2) - 3(х0 + хn)
или
d" = n(n + 1) - 4(x2 + x4 + x6 +... + хn-1) - (3х0 + хn)
в зависимости от того, является ли п четным числом или нет.
I. Если число столбов нечетно (n - четное), то разделим множество n+1 чисел
0,1,2, ...... , n
на три части:
множество С1, охватывающее n/2 - 1 чисел; 0, 1,2,...,(n-4)/2
множество С2, охватывающее 2 числа: (n-2)/2, n/2,
множество С3, охватывающее n/2 чисел:
(n+2)/2, (n+4)/2, (n+6)/2,....,n
и обозначим:
произвольную перестановку чисел множества С1 через
x2, x4, x6,...,xn-2
произвольную перестановку чисел множества С2 через
x0, xn
произвольную перестановку чисел множества С3 через
x1, x3, x5, ..., xn-1
Тогда
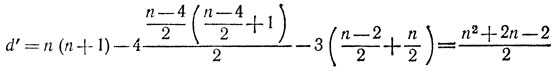
равно длине максимального пути, который можно пройти, вбивая гвозди. Дорогу эту, начиная от одного из столбов множества С2, проходим поочередно переходя от столбов множества С1 к столбам множества С3 и наоборот, а закончим на втором из столбов множества С2. При этом длина пути не зависит от того, в какой очередности мы исчерпываем столбы множества С1 и столбы множества С3.
II. Если число столбов четное (n - нечетное), то обозначим произвольную перестановку чисел
0, 1, 2, ...., (n-3)/2
через
x2, x4, x6,...,xn-1
произвольную перестановку чисел
(n+3)/2, (n+5)/2, (n+7)/2,....
через
x1, x3, x5,...,xn-2
и примем
x0=(n-1)/2, xn=(n+1)/2
Тогда
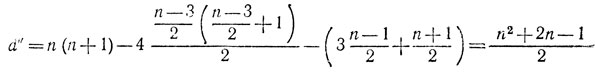
равно длине максимального пути, который можно пройти, вбивая гвозди. Эту дорогу мы также можем пройти по-разному.
65. Поставим кирпич на стол так, как показано пунктиром на рис, 129, а, и проведем карандашом риску на ребре стола в том месте, где заканчивается ребро кирпича. Затем будем передвигать кирпич вдоль этого ребра стола до тех пор, пока вершина кирпича не совпадает с риской (новое положение кирпича показано на рисунке сплошной линией), и после этого измерим линейкой расстояние от вершины A стола до вершины С сдвинутого кирпича.
Укажем еще одно решение. Совместим ребро дощечки с двумя противоположными вершинами верхнего основания кирпича так, чтобы дощечка краем упиралась в одну из вершин, и отметим на дощечке риской отрезок, равный длине диагонали верхнего основания кирпича. После этого сдвинем дощечку на расстояние, равное длине этой диагонали (рис. 129, б), и измерим расстояние AM.
Рис. 129
66. Если на коробке, имеющей форму прямоугольного параллелепипеда, мы нарисуем след ленточки, то на развертке коробки этот след образует прямую линию (см. рис. 130, на котором две грани коробки повторены). Из рисунка легко заметить, что
1° длина ленточки равна 2 √((а+с)2 + (b+с)2),
2° тангенс угла, под которым ленточка пересекает ребра, равен (a+c)/(b+c) или (b+c)/(a+c),
3° ленточку можно перемещать по коробке не растягивая ее, 4° длина ленточки будет тогда наименьшей, когда c<а и c<b т. е. когда по два отрезка ленточки проходят по самым большим граням коробки,
Рис.130
Рис. 131
66а. Совершенно очевидно, что шнурки нельзя перемещать, не растягивая их, так, чтобы какой-либо из их отрезков перестал быть параллельным соответствующему ребру коробки. Нельзя также изменить только положение точек скрещивания шнурков на крышке и основании, ибо и в этом случае один из кусков шнурка, соединяющих эти точки, должен был бы удлиниться (рис. 131).
67. Ограничимся случаем, когда мы располагаем гирей в 1 кг.
Пусть АС=l (рис. 132) обозначает расстояние между центром масс С не загруженного безмена и точкой А подвеса груза. Пусть Q - масса
безмена. Центр масс безмена определяем экспериментальным путем.
Предположим, что при нагрузке безмена в точке А гирей в 1 кг безмен, подпираемый в точке В, окажется в равновесии. Длину отрезка А В обозначим через а.
Пусть D обозначает точку опоры безмена, находящегося в состоянии равновесия при нагрузке его в точке А произвольным грузом в р кг. Длину отрезка AD обозначим через х.
Из условия равновесия для обоих приведенных выше случаев следует равенство моментов
a=Q(l-а), рх=Q(l-х),
откуда
px/a=(l-x)/(l-a) (1)
Для нанесения шкалы на стержень безмена начертим на бумаге отрезок АС, обозначим на нем точку В и из концов А и С этого отрезка проведем два параллельных луча Am и Сn, как показано на рис. 133.

Рис. 132
Рис. 133
Затем на луче Сn, начиная от точки С, отложим равные отрезки произвольной длины С1, 12, 23, ... и через точку L этого луча, соответствующую единице, а также через точку В отрезка АС проведем прямую, которая пересечет луч Аm в точке К.
Из подобия треугольников АКВ и CLB получим для отрезка AK=k соотношение
k=a/(l-a), (2)
при этом всегда l>а.
Шкалу на луче Сn спроектируем теперь на прямую АС, принимая точку К за центр проекции. Пусть 5 - проекция точки Р. Из подобия треугольников AKS и CPS, учитывая равенство (2), получим
p×AS/a=(l-AS)/(l-a)
Сравнивая полученный результат с равенством (1), мы замечаем, что AS=х, а следовательно, S является той точкой, в которой необходимо подпереть безмен, нагруженный грузом в р кг.
Итак, путем проектирования равномерной шкалы, описанным выше способом мы можем нанести на безмен шкалу, учитывующую не только целое число килограммов.
Из приведенных выше рассуждений следует, что требование постоянной толщины и однородности стержня безмена было в условии задачи излишним.
68. Как видно из рис. 134, мы имеем АО=√(ОB2-АВ2). Так как А В равно ширине s подвижной линейки, а наименьшее ОВ равно расстоянию h гвоздя от неподвижной линейки, то минимальное АО равно √(h2-s2).
Рис. 134
69. Первичное деление прямоугольника на две части является очевидным (рис. 135).
Заметим теперь, что если прямоугольник первичным образом разделен более чем на две части, то каждая из его сторон должна пересекать по крайней мере одну из делящих линий. Другими словами, не определяет, например, первичного деления такая конфигурация, как
на рис. 136, при которой вертикальная линия деления отсекает от целого прямоугольника левый прямоугольник, внутри которого мы уже не имеем дальнейших линий деления, а в правом заштрихованном прямоугольнике мы имеем произвольное расположение делящих линий.
Рис. 135
Рис. 136
Из сделанного замечания следует, что не существует первичного деления на три части (рис. 137), ибо при каждом делении прямоугольника на три части по крайней мере одну из сторон прямоугольника не пересекала бы ни одна из линий деления и поэтому деление не было бы первичным. Из этого замечания также следует, что не существует первичного деления прямоугольника на четыре части.
Первичное деление прямоугольника на пять частей, конечно, возможно (рис. 138). Подобным же образом возможно первичное деление прямоугольника на семь и более частей, причем вопрос усложняется потому, что можно привести различные способы деления прямоугольника на то же самое число частей. Например, на рис. 139 показаны два различных первичных деления на семь частей, а на рис. 140 - четыре различных первичных деления на восемь частей.
Перейдем теперь к решению задачи, т. е. к первичным делениям квадрата на некоторое число равных частей.
Деление на пять равных частей. Пусть дан квадрат со стороной 1. Предположим, что квадрат этот разделен первичным образом на пять равных частей (рис, 141).
Рис. 137
Рис. 138
Рис. 139
Рис. 140
Ограничимся исследованием симметричного деления. Обозначая через сторону центрального квадратика, получим, что x2=1/5, откуда х=√5/5. Поэтому размеры четырех оставшихся прямоугольников будут следующие:
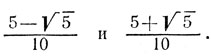
Деление на семь равных частей. Снова возьмем квадрат со стороной 1, предполагая, что он разделен на семь равных частей по схеме, приведенной на рис. 142. Обозначим стороны прямоугольников, на которые разделен квадрат, так, как указано на рисунке.
Рис. 141
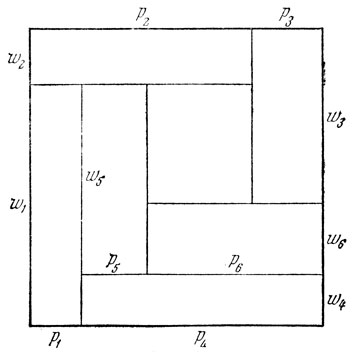
Рис. 142
Пусть w1=x. Тогда р1=1/7х и далее последовательно получаем
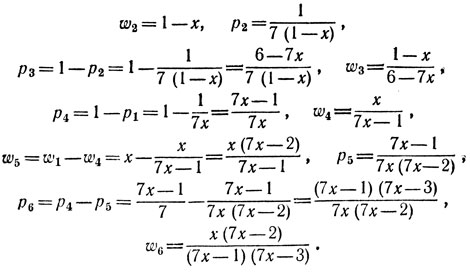
Так как w3+w4+w6=1, то
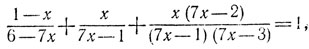
откуда после простых преобразований получаем уравнение 196x3-294x2+128x-15=0.
Одним из корней этого уравнения является х=1/2. Корень этот не дает решения задачи, так как при x=1/2 получаем w1=w2 следовательно p1=p2 и деление квадрата не будет первичным. Остальными корнями полученного уравнения являются
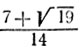 и
и 
Рис. 143
Рис. 144
Так как согласно условию задачи, должно быть x>3/7=6/14 (ибо в противном случае было бы p6<0), то в качестве решения подходит только число (7+√19)/14. Ему соответствует решение задачи, пред ставленное на рис. 143. Оно указано профессором Я. Минусинским.
Можно доказать, что не существует первичного деления на семь равных частей такого типа, как изображено на рис. 139 справа. Однако может быть и существует первичное деление на семь равных частей какого-либо иного типа.
Рис. 145
Деление на восемь равных частей. Перейдем теперь к первичному делению квадрата на восемь равных частей.
Предположим, что возможно деление квадрата со стороной 1 по симметричной схеме, изображенное на рис. 144; каждый из частичных прямоугольников имеет тогда площадь, равную 1/8.
Принимая во внимание симметрию, мы имеем w1=1/2 и следовательно, p2=1/4. Пусть w1=x. Тогда
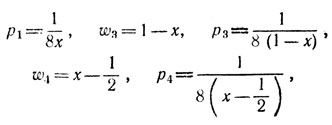
а так как р4=р3-р1, то в конечном счете
откуда х(1-х)=x(x-1/2)-(x-1/2)(1-х), и наконец, после некоторых преобразований,
6х2-6х+1=0,
Из последнего уравнения получаем x1,2=(3±√3)/6 причем, как должно было x>1/2, то только корень x2=(3+√3)/6 так удовлетворяет условиям задачи.
На рис. 145 изображено первичное деление квадрата на восемь равных частей, причем указаны размеры отдельных прямоугольников.
Рис. 146
Кроме рассмотренного выше способа деления, возможно еще иное первичное деление квадрата на восемь равных частей, представленное на рис, 146; мы получаем его подобным же образом, как и предыдущее.
Рис. 147
70. Задача решается следующим образом: устанавливаем люнетку в точке О данного участка (рис. 147) и измеряем наклон участка в произвольно выбранном направлении ОС1. С этой целью устанавливаем в точке A1 в том же направлении веху и измеряем расстояние d1 и разность уровней h1 между точками О и A1. Наклон участка определяем как частное t1=h1/d1 . Затем поворачиваем люнетку на 90° и в направлении ОС2, перпендикулярном к ОС1, измеряем наклон участка! выражающийся числом t2=h2/d2
Принимая луч OС1 за ось Ох, ОС2 за ось Оy, находим вектор G компонентами t1, t2 на этих осях; направление этого вектора является направлением наклона участка, а его длина, т. е. число √(t21+t22) равна наклону участка.
А вот обоснование этого метода. Пусть р - линия уровня, проходящая через точку О, q - линия наклона, q' - проекция линии наклона на горизонтальную плоскость П, β - угол наклона, а а - пусть будет неизвестным углом, который образует направление OС2 с направлением q'. Имеем

откуда
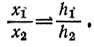
Кроме того, имеем
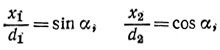
поэтому
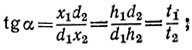
следовательно, приведенный выше метод отыскания направления наклона, правильный. Наконец, вычисляем наклон участка:
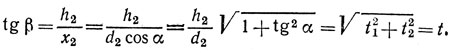
71. Предположим, что город М соединен отрезками МЛ, MB, MC, MD, ... с городами А, В, С, D, ... (рис. 148).
Соединим отрезком точки А и В. Имеем АМ<АВ и ВМ<АВ, так как в противном случае вместо по крайней мере одного из соединений AM и ВМ имело бы место соединение А В,
Из неравенств
АМ<АВ и ВМ<АВ
следуют неравенства
γ>α и γ>β;
складывая эти неравенства и еще равенство γ=γ, получаем
3γ=α+β+γ или 3γ>180°,
следовательно, γ>60°.
Коль скоро, однако, имеет место неравенство γ>60°, то в точке М могут сходиться вершины самое большее 5 треугольников, что и требовалось доказать.
Рис. 148
72. Могут существовать три рода железнодорожных сетей, изображенные на рис. 149.
1) В первом случае каждый из городов может быть узлом, В котором сходятся четыре пути, следовательно, различных сетей подобного рода будет пять,
2) Во втором случае город, который будет узлом и в котором сходятся три линии, можно соединить с тремя другими городами четырьмя способами (число сочетаний из четырех элементов по три), а пятый город в каждом из этих случаев можно соединить с каждым из этих трех городов, следовательно, всего возможных соединений существует 4×3=12. А так как каждый из пяти городов может быть узлом, то различных сетей рассматриваемого нами рода будет всего 5×12=60.
3) В третьем случае в сети, соединяющей города, можно произвольно изменять очередность городов, а следовательно, получим всего столько сетей, сколько существует перестановок из пяти элементов, т. е. 5!=120. Но каждая перестановка и обратная перестановка определяют ту же самую сеть, поэтому различных сетей будет 120:2=60.
Всего сетей существует 5+60+60=125.
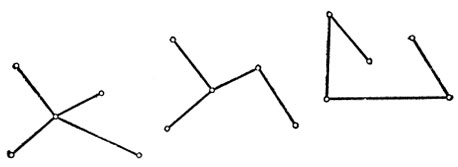
Рис. 149
Рис. 150
Рис. 151
73. 1) Из всех треугольников с постоянным основанием и постоянной высотой наименьший периметр имеет равнобедренный треугольник. Для доказательства достаточно заметить (рис. 150), что точка Р, лежащая на касательной к эллипсу, проходящей через точку S, лежит вне этого эллипса, вследствие чего
KP+PL>KS+SL.
2) Из приведенного выше рассуждения следует, что если точки K, L, М являются вершинами равнобедренного треугольника с основанием KL=2p и высотой MO=h (рис. 151), то сеть KS+LS+MS короче сети AP+LP+MP.
3) Введем обозначения (рис. 151):
OS=x, KS+LS+MS=m;
тогда получим
2√(p2+x2)+h-x=m;
откуда
3x2-2(m-h)x+4p2-(m-h)2=0;
вследствие этого (из условия действительности корней) получаем
(m-h)2-3p2≥0
Это условие ведет к следующему ограничению для m:
m≥h+p√3
причем m получает наименьшее значение при
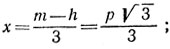
тогда ∠OKS=30°.
4) В случае соединения городов А, В, С, D железнодорожной сетью без узлов кратчайшим был бы путь, представленный на рис. 152 (или же один из трех иных путей, который можно получить из этого,
поворачивая его на 90°, 180° или 270° вокруг центра квадрата). Длина такого соединения равна 300 км.
5) Предположим, что города А, B, С, D соединены железнодорожной сетью с одним узлом S. Узел этот должен быть соединен по крайней мере с тремя из городов A, В, С, D, ибо в противном случае, выпрямляя дорогу, ведущую через узел, мы получили бы более короткую сеть. Пусть узел 5 будет соединен с городами А, В, С (рис. 153). Тогда город D может быть соединен или с одним из городов A и С, или же с узлом S.
Рис. 152
Рис. 153
В первом случае согласно тому, что доказано в пунктах 2 и 3(p=h=50√2 км), длина кратчайшей сети была бы равна
100+50√2(1+√3)≈293,2 км.
Во втором случае согласно доказанному в пункте 1 сеть будет кратчайшей, если точка 5 будет лежать на оси симметрии стороны А В квадрата и на оси симметрии стороны ВС квадрата, т. е. если она будет лежать в центре квадрата; тогда длина сети будет равна
2×100√2≈282,8 км.
6) Предположим, что города A, В, С, D соединены железнодорожной сетью, содержащей два узла S1 и S2. Узел S1 должен быть соединен по крайней мере с тремя из точек A, В, С, D, S2, в противном случае выпрямление дороги, ведущей через узел, дало бы более короткую сеть.
Пусть узел соединен с городами А и В и с узлом S2. Тогда узел S2 будет соединен с городами С и D и сеть будет иметь конфигурацию, представленную на рис. 154.
Если точки и S2 не лежат на оси симметрии стороны квадрата AВ, то, как это следует из рассуждений пункта 1, сеть с узлами и S2 длиннее сети с узлами Р1 и Р2. Следовательно, эта сеть будет кратчайшей тогда, когда точки Р1 и Р2 расположены симметрично относительно центра квадрата, так что ∠P1AB=∠P2CD=30°. Длина сети равна (см. пункт 3, где принимаем, что p=h=50):
100(1+√3)≈273,2 км.
7) Увеличение числа узлов более чем на 2 вызывает удлинение сети. Поэтому длина кратчайшей сети, которая может соединить города А, В, С, D, согласно условию задачи, равна
100(1+√3)≈273,2 км.
Она может быть реализована двояко, как это иллюстрирует рис. 155.
Рис. 154
Рис. 155
74. Кратчайшим путем на шаре (земном) является дуга большого га, т. е. круга, образованного пересечением шара с плоскостью, проходящей через центр шара.
Рис. 156
Так как самолет, вылетающий из Осло, исчез из глаз зрителей, находящихся на аэродроме, в точке горизонта, лежащей точно на запад.
то самолет летел по большому кругу, пересекающему меридиан в Осло (α=10°43' восточной долготы) под прямым углом.
Пусть на рис. 156 S и О соответственно обозначают центр земного шара и точку, в [которой лежит Осло, и пусть Q, G, О' соответственно обозначают точки пересечения с экватором: большого круга, по которому летел самолет, нулевого меридиана, а также меридиана, проходящего через Осло.
Легко заметить, что угол QSO' прямой; отсюда имеем
∠GSQ=90°-∠GSO'=90°-10°43'=79°17'
Плоскость OSQ Наклонен а к плоскости экватора под утлом β=59°55'- под этим углом относительно восточного направления должны ожидать самолет зрители, находящиеся на аэродроме в Эквадоре.
75. При полном затмении Солнца размеры Солнца и Луны кажутся нам приблизительно одинаковыми. Отсюда следует, что диаметр Солнца в 387 больше Диаметра Луны, а отношение их объемов равно 3873≈58×106.
76. Самый короткий день во Вроцлаве (т. е. время, которое протекает между восходом и заходом Солнца в один и тот же день) наступит конечно, тогда когда Солнце окажется в зените на тропике Козерога (ежегодно приблизительно 23 декабря).
Для определения длины этого дня мы должны знать географическую Вроцлава φ=51°07' и угол, который образует плоскость экватора земного шара с плоскостью эклиптики, δ=23°27' (значения обоих углов даны приближенно).
Пусть на рис. 157 буквы О и М соответственно обозначают ценю земного шара и положение Вроцлава на этом шаре, и пусть прямая NS обозначает ось вращения земного шара. Пусть плоскостью эклиптики будет плоскость Oxy; плоскость экватора, проходящая через точку R, образует с ней угол δ. Плоскость OWZ, перпендикулярная к плоскости эклиптики и к направлению Ох падения лучей Солнца, отделяет на земном шаре освещенную часть от неосвещенной. Вроцлав на восходе солнца проходит через точку Ζ по дуге и на заходе Солнца оказывается в точке W.Длина дня во Вроцлаве пропорциональна углу ΖΟ1W.
Длина самого короткого дня во Вроцлаве, конечно, пропорциональна длине дуги ZMW параллели, проходящей через Вроцлав, или же, короче, величине угла 2β=ΖΟ1W.
На основании рис. 157 из прямоугольных треугольников OO1M, O1PW, OO1P мы легко получаем
откуда
β=57°27'35",
Для длины t самого короткого дня во Вроцлаве получаем пропорцию
t:180° (T=24 ч),
откуда
t=7 ч 39 мин 40 с.
Стоит еще заметить, что истинная длина самого короткого дня во Вроцлаве больше вычисленной нами приблизительно на четверть часа. На это влияет так называемая астрономическая рефракция, возникающая из-за преломления солнечных лучей в слоях атмосферы, окружающей земной шар.
Рис. 157
77. Клеткой, смежной с белой клеткой, является черная, и наоборот. На шахматной доске с нечетным числом клеток число белых клеток не равно числу черных, поэтому требуемое в задаче перемещение пешек невозможно.
78. Ответ на поставленный в задаче вопрос отрицателен: ни одна из пешек не изменит своего положения. При этом безразлично, считаем ли мы соседними только такие две клетки, которые прилегают друг к другу сторонами, или также и клетки, соприкасающиеся в вершинах. Во втором случае следует, однако, предположить, что шахматная доска (квадратная) состоит более чем из четырех клеток.
Доказательство для обоих случаев можно вести совместно следующим. образом.
Обозначим через (t, k) клетку, расположенную в i-й "строке" и в k-м "столбце" шахматной доски с числом клеток n2 (причем n>2), а через F(i, k) обозначим клетку, на которой установим пешку, стоявшую раньше в клетке (i, k).
Предполагая, что F(1, 1)= 1, 1), F (n, 1 )=(n, 1) и что преобразование F(i, k) сохраняет соседство клеток, нужно доказать, что
F(i, k)=(i, k) для i=1, 2, ...,n: k=1, 2, ..., n.
Сразу видно, что число клеток, соседних с некоторой определенной клеткой шахматной доски, меньше для угловых клеток, чем для остальных крайних клеток шахматной доски, а для последних ^меньше, чем для внутренних клеток шахматной доски. Так как при новой расстановке ни одна из пешек не может иметь меньше соседних пешек, чем имела прежде, то если клетка (t, k) - внутренняя, то клетка F(i, k) также является внутренней, или обе они являются угловыми, или, наконец, обе расположены по краям и не являются угловыми.
Последовательность (1, 1), (2, 1), ..., (n, 1) является последовательностью очередных смежных клеток, расположенных вдоль края шахматной доски. Тем же самым свойством должны обладать клетки последовательности F(1, 1), F(2, 1) F(n, 1). Но (1, 1)=(1, 1), а с клеткой
(1. 1) будут смежными (при условии, что n>2) только две клетки края: (1, 2) и (2, 1); функция F(2, 1) может принимать, следовательно, только одно из этих двух значений. Рассмотрим эти два случая.
a) F(2, 1)=(1, 2). В этом случае клетка F(3, 1), как крайняя, смежная с клеткой F(2, 1), т. е. с клеткой (1, 2), и отличная от (1, 1), должна была бы совпасть с клеткой (1, 3); подобным же образом получилось бы F(4, 1) = (1, 4) и т. д. Наконец, угловая клетка F(nf 1) была бы клеткой (1, k), вопреки условию, что F(n, 1)=(n, 1). Случал а), следовательно, не может иметь места, поэтому будет иметь место следующий случай,
б) F(2, 1)-(2, 1). Тогда, рассуждая так же, как и в случае а), поочередно получаем
F(3. 1)=(3, 1), F(4, 1)=(4, 1), F(n, 1)=(k, 1),
т. е. окажется, что пешки первого столбца останутся на месте.
Равенства F(i, 1)=(1, 1), где i=1, 2,...., n, в свою очередь влекут
за собой равенства F(iy 2)= (/, 2) для /= 1, 2, ..., л. Действительно, клетка /=* (1, 2) является крайней клеткой, смежной с клеткой (1, 1) П отличной от клетки (2, 1), следовательно, F( 1, 2)=(1, 2); клетка f (2, 2) является смежной с клетками F(2} 1) и ?(1,2), или с клетками (2, 1) и (1, 2) и отличной от (1, 1), следовательно, F(2, 2)=(2, 2), и т. д.
Таким же образом проверяем равенство F(i, k)=(i, k) для следующих столбцов шахматной доски.
Обобщение. Полученный результат позволяет нам сделать некоторый общий вывод.
Рассматриваем функцию ?, которая каждой клетке шахматной доски ставит в соответствие некоторую определенную клетку той же шахматной доски таким образом, что двум различным клеткам соответствуют различные клетки и что смежным клеткам соответствуют тоже смежные клетки.
Такими функциями (преобразованиями) являются, например, тождественное преобразование (или преобразование, при котором каждая клетка остается на месте), симметрия относительно каждой из четырех осей симметрии квадрата шахматной доски, а также повороты на 90 , 180° и 270° вокруг центра шахматной доски.
Докажем, что каждое преобразование F рассматриваемого нами типа должно быть одним из восьми названных выше преобразований.
Действительно, пусть F будет таким преобразованием. Как мы знаем, угловым клеткам соответствуют угловые клетки, следовательно, могут иметь место только следующие случаи:
I. Преобразование F оставляет клетку (1, 1) на месте. В этом случае имеет место одна из двух возможностей:
1) Клетка (n, 1) тоже остается на месте. Тогда преобразование, как мы это доказали выше, является тождественным.
2) Клетка (n, 1) совпадает с другой угловой клеткой. Это может быть только клетка, (1, n), в чем убеждаемся, рассуждая так же, как и раньше, т. е. рассматривая последовательность F(1, 1), F(2, 1), ... ..., F(n, 1). Выполним, после преобразования F, еще преобразование симметрии S1 относительно главной диагонали шахматной доски, т. е. диагонали, проходящей через (1, 1) и (n, n).
Произведение* F×S1 является преобразованием рассматриваемою типа, которое каждую из клеток (1, 1) и (n, 1) оставляет на месте, следовательно, это тождественное преобразование h
F×S1=I.
* (Пусть A, В обозначают отображения (преобразования) некоторого множества на себя. Произведением А*В называется преобразование, получаемое в результате выполнения сначала преобразования A, а затем преобразования В. Если, например, А является осевой симметрией на плоскости, то A×A, т. е. А2, является тождественным преобразованием; если А и В - преобразования симметрии относительно пересекающихся осей а и b, то А*В есть вращение вокруг точки пересечения осей а и b на угол, вдвое больший угла, образованного осями. Если I является тождественным преобразованием, а A - произвольным преобразованием, то A×I=I*A=A. Произведение преобразований подчиняется ассоциативному закону, т. е. (A×B)×С=A×(В×С). [Иногда результат последовательного выполнения преобразований A и В (сначала A, затем В) обозначают через В×А или ВА,- Примен. ред.] )
Умножая обе части этого равенства на S1 получаем (F×S1)×S1= I×S1, т. е. F×S21=S1, а так как S21=I, то F=S1, т. е. преобразований F в данном случае является симметрией относительно главной диагонали шахматной доски.
II. Клетка (1, 1) переходит при преобразовании F в клетку (n, n). Пусть S2 обозначает симметрию относительно другой диагонали шахматной доски; она преобразует клетку (n, n) в клетку (1, 1). Следовательно, преобразование F×S2 оставляет клетку (1, 1) на месте, в следствии вне чего согласно 1) имеют место две возможности: произведение F×S2 является единичным преобразованием или же симметрией.
3) Произведение F×S2 есть единичное преобразование, т. е.
F×S2=I
Умножая это равенство справа на S2, получаем
F=S2
т. е. F есть преобразование симметрии относительно диагонали шахматной доски, проходящей через клетки (1, n) и (n, 1),
4) Произведение F×S2 является симметрией S1:
F×S2=S1.
Умножая это равенство справа на S2, получаем
F=S1×S2.
Преобразование F является, следовательно, в этом случае поворотом на 180° вокруг центра шахматной доски, или центральной симметрией относительно этой точки.
III. Клетка (1, 1) переходит при преобразовании F в клетку (n, 1). Тогда преобразование F×S3 где S3 обозначает симметрию относительно горизонтальной оси симметрии шахматной доски, оставляет клетку (1, 1) на месте, и мы снова имеем две возможности:
5) F×S3=I, откуда F=S3, или
6) F×S3=S1, откуда после умножения этого равенства справа на S3 получаем
F=S1×S3
а тогда преобразование F является поворотом на 90° вокруг центра шахматной доски.
IV. Клетка (1, 1) переходит при преобразовании F в клетку (n, 1). Обозначая через S4 симметрию относительно вертикальной оси симметрии шахматной доски, получаем, так же как в случае III, две возможности:
7) F=S4
или
8) F=S1×S4, т. е. преобразование является вращением на 270° вокруг центра шахматной доски.
Мы доказали, что каждое преобразование множества клеток шахматной доски на себя, сохраняющее смежность клеток, является одним из восьми преобразований:
I, S1, S2, S3, S4, S1×S2, S1×S3, S1×S4.
Преобразования эти образуют так называемую группу*.
* (См., например, Александров П. С. Введение в теорию групп,-М.: Наука, 1980,- Примеч, ред, )
Возвращаясь к задаче о пешках, на основе этой теоремы мы сможем сформулировать следующий более общий вывод.
Если при новой расстановке пешек мы должны оставить на старом месте хотя бы одну пешку, не стоящую ни на одной из осей симметрии, или две пешки, не находящиеся на одной и той же оси симметрии шахматной доски, то каждая пешка должна остаться на своем месте.
79. Задача будет решена, если мы укажем способ расположения ладей на шахматной доске, удовлетворяющий условиям 1), 2), 3), 4)., Для простоты введем некоторые термины.
Столбец доски назовем свободным, если на нем не стоит ни одна ладья и если он содержит по крайней мере одну белую клетку, не атакованную по горизонтали. Напротив, столбец назовем занятым, если хотя бы одна белая его клетка занята ладьей, не атакованной по горизонтали никакой другой ладьей. Строку мы назовем свободной, если она свободна от ладей.
На пустой шахматной доске число свободных столбцов совпадает с числом свободных строк. Выпишем сначала над каждым столбцом число белых клеток этого столбца и будем последовательно расставлять ладьи. А именно, очередную ладью ставим в тот столбец, над которым
стоит число, не превосходящее все остальные числа, стоящие над незанятыми столбцами. Если мы добьемся успеха на этом пути, то задача будет решена, так как условия 1), 2), 3), 4) будут удовлетворены. Пример такого расположения ладей изображен на рис. 158. Маленькие кружки на белых клетках обозначают ладьи, а числа в кружках указывают на последовательность их расстановки на доске. Очевидно, что это расположение не единственно.
Однако описанный выше процесс может натолкнуться на определенные трудности.
а) При расположении очередной ладьи все белые поля нужного столбца могут быть уже атакованы, т. е. в этот столбец ставить ладьи согласно условию 3) нельзя, а в силу условия 4) ладью туда поставить необходимо.
В этой ситуации мы пытаемся сдвинуть вертикально одну из уже поставленных ладей на другое белое поле. Если это нам удается, то можно искать место для следующей ладьи. Пример такого рода иллюстрирует рис. 159.
Рис. 158
Здесь после выставления первых четырех ладей (см. первую доску) все белые поля столбцов d и е окажутся атакованными по горизонтали. Поэтому мы ищем среди занятых столбцов такой, где есть белые поля, не атакованные по горизонтали (в нашем примере - это столбец g). Сдвигая 2-ю ладью на поле g5 (см. вторую доску), получаем возможность поставить 5-ю ладью на поле d4 в столбце d. Аналогично, сдвигая 3-ю ладью на поле Ь8 освобождаем место для 6-й ладьи, которую теперь можно поставить на поле е2. Таким способом мы иногда можем преодолеть возникшие трудности и расставить ладьи в соответствии с условиями 1), 2), 3), 4) (как это удалось в нашем примере - см. последнюю доску на рис. 159).

Рис. 159
Рис. 160
б) Может случиться, однако, что в одном или в нескольких столбцах все белые поля атакованы по горизонтали или, более того, в столбцах, в которых мы уже расставили ладьи, не осталось свободных белых клеток, куда ладьи можно переместить. Мы будем говорить тогда, что соответствующий столбец блокирован. В блокированный столбец мы не можем поставить ладью, не нарушив условие 3), а также не можем сдвинуть ладьи в уже занятых столбцах.
Мы покажем на примере, как преодолеть подобную трудность. На первой доске рис. 160 столбец е блокирован: все белые поля этого столбца атакованы (2-й, 4-й и 5-й ладьями), и притом мы не имеем возможности сдвинуть угрожающие нам ладьи. В этом случае мы снимаем все эти ладьи и вообще отказываемся ставить ладьи как на блокированный до этого столбец, так и на столбцы и строки, в которых стояли снятые ладьи. В нашем примере это: столбцы b, с, d и е и строки 2, 3 и 4. Заметим, что при этом всегда число строк, в которые мы запрещаем ставить ладьи, меньше числа таких же столбцов, а также, что на пересечении "вычеркнутых" столбцов и свободных от ладей строк стоят черные поля. Поэтому нет опасности, что при расстановке новых ладей они будут атаковать по горизонтали белые поля в "вычеркнутых" столбцах.
Может случиться так, что в "вычеркнутых" столбцах остались белые поля, атакованные по горизонтали ладьями, поставленными раньше, но не убранными при "снятии блокады". В соответствии с условием 4), эти поля должны быть атакованы по вертикали. Однако эти столбцы вычеркнуты, т. е. мы не можем ставить в них ладьи. Такую ситуацию мы назовем вторичной блокировкой. В нашем примере поле b1 (вторая доска рис. 160) в вычеркнутом столбце b атаковано по горизонтали ладьей 1. Имеются два пути снятия вторичной блокады.
Сначала мы проверяем, не осталось ли свободное невычеркнутое белое поле в столбце, где расположена ладья, участвующая во вторичной блокировке. Если такое поле имеется, мы переставляем на него эту ладью, после чего продолжаем ставить новые ладьи. Если же поля, о котором говорилось выше, не имеется, то мы вычеркиваем строку и столбец, где расположена ладья, саму ладью мы при этом, конечно, снимаем. В нашем примере (рис. 160) ладья 3 может быть сдвинута на поле а8, чем вторичная блокада снимается. А если бы поле а8 было черным, то нам пришлось бы снять эту ладью и зачеркнуть столбец а и строку 1. В обоих случаях при дальнейшей расстановке в нашем примере ладей мы не встретимся ни с какими трудностями.
Уничтожая вторичную блокировку и вычеркивая при этом определенные столбцы и строки, мы получаем возможность продолжать расстановку ладей.
В случае повторного возникновения блокады, первичной или вторичной, мы применяем тактику, описанную выше.
Можно показать, что в результате этих операций минимум одна ладья останется на доске, так что мы не нарушим соответствующего условия. Заметим сперва, что, ставя ладьи в свободные столбцы, в которых белых клеток не больше чем в других свободных столбцах, мы последнюю ладью поставим в столбец, целиком состоящий из белых полей. Мы всегда сможем поставить ладью в этот столбец, независимо от того, встречались ли мы в процессе расстановки ладей с блокировками одного или обоих типов, или нет.
Пусть, поставив n-1 ладью, мы ни разу не пришли к ситуации блокировки. Все расставленные ладьи стоят в разных столбцах и строках; следовательно, останется только одна свободная строка и один свободный столбец, который, очевидно, целиком состоит из белых полей. Поэтому ладью можно поставить на клетку, имеющуюся в пересечений этого столбца со свободной строкой, в результате чего мы получим нужную расстановку ладей.
Если же у нас появлялись блокировки, то "вычеркивая" указанные строки и столбцы и сдвигая оставшиеся, мы получим прямоугольную доску, у которой число строк больше числа столбцов. Последняя ладья снова ставится в столбец, состоящий из белых полей; поскольку до этого поставлено было не больше n-1 ладей, то это не составляет затруднений.
Легко видеть, что приведенное решение годится не только для квадратных, но также и для прямоугольных досок, число строк у которых больше числа столбцов.
80. Воспользуемся следующим свойством: касательная к эллипсу в произвольной точке образует одинаковые углы с отрезками, соединяющими эту точку с фокусами эллипса. Это означает, что бильярдный шар, посланный из фокуса F1 должен, оттолкнувшись от края, попасть в фокус F2 (на рис. 161 путь бильярдного шара обозначен пунктиром). Поэтому предположение, что задача имеет решение, как показывает этот же рисунок, противоречит законам отражения, ибо требует, чтобы угол падения был больше угла отражения.
81. Всего учеников в классе 25. Так как 6 учеников имеют не удовлетворительные оценки по математике, то учеников с оценками по крайней мере удовлетворительными всего 19; спортсменов в классе не более 19. "Спортсменоучеников" (если считать за единицу один вид спорта, которым занимается один ученик) в классе всего 17+13+8=38, а так как ни один ученик не занимается сразу всеми тремя видами спорта, то, следовательно, учеников, занимающихся спортом - ввиду предыдущего замечания - всего 19 и каждый из них занимается одновременно двумя видами спорта.
Теперь уже легко ответить на вопрос, поставленный в задаче.
а) Ни один ученик в классе не имеет отличной оценки по математике.
б) Из 19 спортсменов 17 умеют ездить на велосипеде; поэтому только два ученика умеют одновременно плавать и ходить на лыжах, а следовательно, два пловца умеют ходить на лыжах.
Рис. 161
82. В первый день бегуны завершили пробег в порядке А, В, С. На второй день порядок был В, С, А, а на третий - С, А, В. Результаты этих состязаний таковы, что А обогнал В в двух случаях из трех возможных; аналогично, в двух из трех случаев В обогнал С и в двух из трех случаев С обогнал А.
Возможно ли, чтобы аналогичные результаты имели место в трех из четырех забегов, т. е. в 75% (или более) всех забегов?
83. Невозможно, чтобы все члены клуба образовали один класс, т. е. чтобы они все имели одинаковое число побед, ибо число розыгрышей (45) не делится на 10.
Невозможно также разделить спортсменов на девять классов. Действительно, если бы было девять классов, то в одном классе было бы два игрока, а в остальных восьми - по одному игроку. Это противоречит условию задачи. Действительно, засчитаем каждому игроку по одному очку за каждый выигрыш. Девять игроков, представляющих девять классов, не могли бы иметь ни 0+1+2+ ...+8=36, ни 1+2+3+... ,..+9=45 очков, ибо тогда десятый игрок имел бы 9 или 0 очков и было бы десять классов. Те же самые девять игроков, однако, не могут иметь 0+1+...+i+ (i+2)+.. .+9=36+8-i очков, ибо тогда девятый игрок должен был бы иметь i+1 очков и снова было бы десять классов.
Разбиение на 7 классов
Приведем примеры разбиения на 7 и на 3 класса. Игроки обозначены буквами. Цифрой 1 на пересечении строки k и столбца i обозначен выигрыш игрока, находящегося в строке k над игроком, находящимся в столбце i, а цифрой 0 обозначен проигрыш.
Разбиение на 3 классов
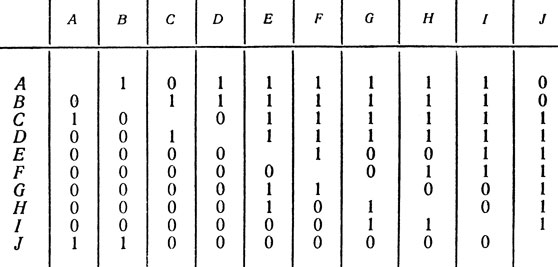
Какие можно привести примеры разбиения игроков на 10, 8, 6, 5, 4 и 2 класса?
84. Сначала докажем с помощью математической индукции, что всегда какая-нибудь команда является чемпионом. Пусть в спортивном объединении будет n команд, Соберем в одной комнате капитанов этих команд, а одного из них (назовем его К) попросим покинуть комнату вместе с капитанами всех команд,.. непосредственно побежденных командой К. В комнате останется, следовательно, n' капитанов; имеем n'<n. Если теорема верна для всех n'<n, то в комнате находится капитан - чемпион по отношению ко всем остальным, оставшимся в комнате. Так как он остался в комнате, следовательно, он является непосредственным победителем над K, а косвенным над иными, которые покинули комнату,- следовательно, он является чемпионом спортивного объединения всех n команд, что мы и хотели доказать
Доказательство 2) является таким же легким. Обозначим все команды через D1, D2, ..., Dn. Пусть команда D1 непосредственно побеждает наибольшее число команд, например команды D2, D3, ..., Dm (и не побеждает непосредственно остальные команды). Следует доказать, что команда Dx косвенно побеждает команды Dm+1, ..., Dn. Предположим обратное, что, например, команда Dm+1 не побеждена ни командой D2, ни командой D3, ..., ни командой Dm, т. е. непосредственно побеждает все эти команды. Так как D1 не побеждает (непосредственно) Dm+1, следовательно, Dm+1 побеждает D1, или Dm+1 непосредственно побеждает больше команд, чем D1 вопреки предположению о D1. Полученное противоречие доказывает 2).
85. Вопрос нужно понимать так: в кубковой системе может случиться, что игрок, который заслуживает второй приз, потому что он сильнее, чем все остальные игроки, за исключением чемпиона, встретился с чемпионом до финиша, т. е. в случае восьми игроков, в первом или во втором туре; в таком случае, второй приз будет выдан несправедливо. Это может случиться тогда и только тогда, когда при жеребьевке для определения партнеров игрок, который заслуживает серебряной медали, т. е. второго места, попадает в ту же подгруппу из четырех игроков, что и чемпион.
Обозначим чемпиона через Ч, а "истинного" серебряного призера - через С; так как в группе, в которую попал Ч, кроме него имеется всего 3 места, на каждое из которых может попасть С, то из семи возможных для С мест 4 благоприятны для него, а 3 - нет. Вероятность того, что С получит второй приз, равна, следовательно, 4/7=0,5714 ..., т. е. чуть больше 57%.
Рис. 162
86. На рис. 162 на горизонтальной оси откладываем дорогу: влево - на почту, вправо - к сельсовету. На вертикальной оси откладываем время. Линии OР1 и OO'Р2 обозначают дорогу посыльных. Если велосипедист сначала будет догонять посыльного, вышедшего раньше, то его дорогу определит линия КА1B1C1D1; если же он будет сначала догонять посыльного, вышедшего позже, - то линия KA2B2C2D2. Из рисунка видно, что велосипедист должен выбрать вторую возможность,— и даже тогда, когда он должен будет передать посланцам только деньги, т. е. тогда, когда его дорога закончится в точке Е1 или Е2.
87. Так как каждая собака бежит под прямым углом к направлению движения собаки, которая ее догоняет, а та, которая догоняет, бежит прямо к убегающей, то догоняющая приближается к соседней собаке со скоростью 10 м/с и поймает ее по прошествии 10 с. Вследствие этого путь каждой собаки равен 100 м. В каждый момент четыре собаки образуют квадрат. Этот квадрат вращается и уменьшается: его стороны уменьшаются равномерно со скоростью 10 м/с. Пути пересекутся в центре S первоначального квадрата. Это будут кривые линии (логарифмические спирали). Они не пересекутся раньше, ибо если бы какая-нибудь собака пересекла след другой, это означало бы, что она была бы в этом месте раньше, а это невозможно ввиду равенства в каждый момент расстояния всех собак от S.
88. Пусть α обозначает мгновенный угол между направлением PQ и дорогой корабля Q (рис. 163), а у — скорость кораблей Р и Q в этот же момент. На взаимное сближение кораблей влияет скорость у корабля Р, направленная на Q, а также компонента υ cos α скорости корабля Q, обе одинакового направления. Поэтому скорость сближения кораблей равна υ(1—cos α).
Проекция S точки Р на пути корабля Q перемещается по этому пути со скоростью υ cos α, а корабль Q уходит со скоростью υ, следовательно, расстояние SQ возрастает со скоростью υ (1—cos α). Так как расстояние PQ уменьшается, как мы заметили раньше, с той же скоростью, то сумма PQ+SQ постоянна, а следовательно, равна 10 милям, как и в начальный момент. После бесконечно долгого времени Р совместится с5 и будет равно PQ+SQ=2PQ=10 милям и PQ=5 милям.
Рис. 163
Рис. 164
89. Пусть Р1, Р2 или О1, О2 соответственно обозначают положения обоих кораблей в начальный момент (когда второй из кораблей замечен первым), а также в момент, когда их расстояние наименьшее. Если так, то первый корабль плыл из точки Р1 к O1 по прямой линии Р1O2 (рис. 164). Кроме того, в конечный момент компоненты скоростей обоих кораблей вдоль O1O2 должны быть равны, т. е.
υ1=υ2 sin α, sin α=k
Угол α определяет курс первого корабля. Так как корабли дошли до точек О1, O2 в одно время, то
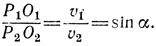
Так как
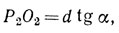
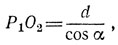
то искомое наименьшее расстояние кораблей равно
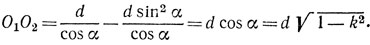
90. Если k имеет такое же значение, как и в предыдущей задаче, то курс сигнализирующего корабля определяется через угол α (рис. 164) следующим образом:
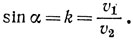
Если же, наоборот, k обозначает отношение скорости замеченного корабля к скорости сигнализирующего корабля, то при курсе, снова определяемом равенством sin a=k, корабли встретятся в точке 02 (рис. 164),
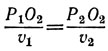
или
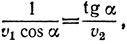
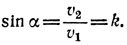
Следовательно, во втором случае курс определяется таким же способом, f как и в первом.
91. В момент, о котором идет речь в задаче, сторожевой корабль находится в точке S, а моторная лодка - в точке М (рис. 165). Лодка движется по сторонам квадрата MN, NW. Сторожевой корабль не догонит лодку на отрезке MN, ибо его скорость для этого слишком мала. Обозначим через а длину стороны квадрата, а через υ - скорость корабля (следовательно, скорость лодки равна 3υ). Точка Р, лежащая на отрезке NW, опасна для лодки, если сторожевой корабль может до нее добраться не позднее лодки, т. е. если
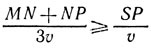
или
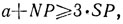
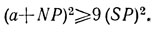
Так как
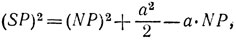
то приведенное выше неравенство эквивалентно следующему квадратному неравенству относительно NP:
Неравенство это выполняется для
следовательно, опасная часть дороги равна 3/16 целого и начинается по прохождении 3/4 дороги, а кончается по прохождении 15/16 дороги.
92. В начальный момент лодка находится в точке М, сторожевой корабль в точке S; лодка должна прибыть к побережью в точке W (рис. 166). Точки М, S, W лежат на одной прямой MS≡SW. Из текста
задачи следует, что лодка должна плыть по сторонам прямого угла MNW, вписанного в окружность диаметра MW.
Рис.165
Рис.166
Путь лодки должен быть по возможности кратчайшим, поэтому первый его отрезок (MN) должен образовать возможно меньший угол с направлением MW. Кроме того, лодка должна наверняка избегать, сторожевого корабля. Поэтому ее путь не должен пересекать аполлониевой окружности TUV, которая является геометрическим местом точек, в которых встречаются корабль и лодка, плывущие соответственно из точек S и М со своими максимальными скоростями по прямым линиям. Центром аполлониевой окружности является точка О, положение .которой на отрезке MW определяем из соотношений
MT=3ST, MV=3SV, OT=OV
Из этих равенств следует, что
MO=9/16 MW
а радиус аполлониевой окружности равен 3/16 MW. Если бы отрезок MN касался окружности MN, то путь лодки равнялся бы
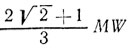
то пусть будет длиннее
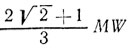
Следует еще только проверить, что если отрезок MN проходит достаточно близко к окружности TUV, то сторожевой корабль не настигнет лодку и на отрезке NW. Оставим это читателям.
Итак, курс лодки, отвечающий условию задачи, определен полностью,
93. Таким удивительным числом является число один, которое можно записать тремя способами:
1, 100% и 57°17'44", 8... (1 радиан).
94. Новый "сантиметр" при измерении может дать ошибку в 1/2 см, так же как и старый, и не в этом следует искать его преимущество. При измерении некоторого отрезка А В конец В, вообще говоря, окажется между штрихами шкалы. Используя новую ленту (рис. 167), мы, без сомнения, припишем этому отрезку длину N см, если N является надписью между штрихами. При использовании же обычной ленты мы должны еще установить, лежит ли В ближе к левому или к правому штриху. В исключительном же случае, когда при использовании новой ленты конец В совпадает со штрихом, лежащим между числами N и N+1 записываем
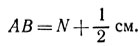
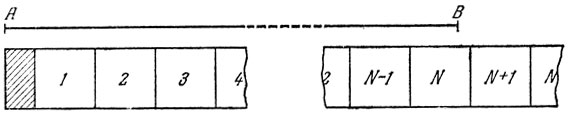
Рис. 167
95. Не существует словарей, содержащих более миллиона слов. Если, например, словарь содержит 500 страниц, то мы откроем его посредине и найдем самое последнее слово на странице 250, предположим, "нарцисс". Первый вопрос должен быть таким: находится ли отгадываемое слово в словаре после слова "нарцисс"? Если ответ будет гласить "да", то мы открываем словарь на странице 375, а если "нет", мы откроем его на странице 125 и опять спросим о расположении загаданного слова по отношению к последнему слову на открытой странице, и т. д. Если в какой-то момент мы получим дробное число страниц (например, 62,5), то мы округлим его до ближайшего большего целого числа. После девяти таких вопросов поиски слова ограничатся одной страницей. Если на этой странице 2 столбца, то .с помощью 10-го вопроса мы определим столбец. В столбце самое большее 64 слова и, следовательно, 16-й вопрос приведет нас к одному слову, которое, если мы еще раньше не отгадали нужное слово, мы и укажем загадавшему его.
Словарь, который мы указали в качестве примера, содержит не более 128*500=64 000 слов. Так как число слов в словаре ограничено миллионом, то в нем может быть не более чем в 16 раз больше слов, чем в словаре, рассмотренном выше (64 000*16=1 024 000). Для словаря с максимальным количеством слов потребуются 4 дополнительных вопроса (24 = 16), т. е. всего 20 вопросов.
Мы видим, таким образом, что доктор Шарадек говорит правду.
96. Каждый студент, одалживающий кому-либо деньги, записывает соответствующую сумму как положительное число, а занимая у кого-нибудь деньги, записывает эту сумму как отрицательное число. Сумма всех записанных чисел дает в конце года положительное или отрицательное сальдо данного студента, причем сумма всех сальдо дает нуль.
Бухгалтерии Шарадека достаточно для выравнивания долгов, а необходимо для этого самое большее шесть выплат. Действительно, предположим, что "наименьший" должник выплачивает всю сумму "наибольшему" кредитору. Тогда, после первой выплаты, общее число должников и кредиторов будет равно самое большее шести, а после пятой выплаты, произведенной по тому же самому принципу, число должников и кредиторов будет равно самое большее двум, вследствие чего самое большее после шестой выплаты все долги будут выравнены. Конечно, может случиться, что после какой-либо очередной выплаты один из кредиторов станет должником, но этот факт не изменит числа кредиторов и должников.
96а. Обозначая буквой р правую чашку весов, а буквой l - левую чашку, получим следующее расположение монет после трех взвешиваний:
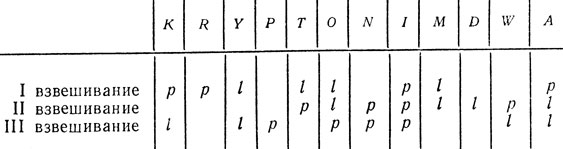
Предположим теперь, что одна монета тяжелее остальных. Тогда, обозначая знаком "О" равновесие чашек, знаком "+" перевес правой чашки весов, а знаком "-" перевес левой чашки весов, будем иметь следующие возможности, в зависимости от того, какая монета (с названием, указанным в соответственном столбце) тяжелее:
Если бы одна монета была легче 1 остальных, то имели бы место следующие возможности:
Так как все расстановки трех знаков в двух приведенных выше таблицах различные, то, предполагая, что только одна монета фальшивая, можно из наличия соответственной расстановки знаков заключить, какая из монет фальшивая, а также тяжелее она или легче остальных.
Из трех элементов можно образовать всего 33=27 сочетаний с повторениями, поэтому две приведенные выше таблицы не охватывают еще трех случаев, а именно:
0 - +, 0 + -, 0 - +
Первый случай - при условии, что по крайней мере 11 взвешенных монет являются одинаковыми,- вызывает равенство всех монет. Следовательно, мастер мог прийти к выводу, что все монеты настоящие, предполагая лишь, что самое большее одна монета фальшивая.
Два остальных случая не могут иметь места, если только одна монета фальшивая.
Поэтому, если выступает один из этих случаев, то можно заключить, что по крайней мере две монеты фальшивые. Если же, однако, имеет место один из этих случаев, то фальшивыми могут быть пары YT, Y W, TW или тройки KTY, RPD и т. д. Обман был обнаружен потому, что мастер обозначил фальшивые монеты двумя из трех букв Т, Y, W; если бы случилось иначе, обман не был бы открыт. Действительно, если бы, например, фальшивыми (и более тяжелыми) оказались монеты K, Р, то результат взвешиваний, представленный символически, был бы следующим:
MYTO<RAKI, MODA=WINT, WYKA=PION,
а тогда мастер считал бы, что фальшивой (и более тяжелой) монетой является R, что не соответствует истине.
Постараемся ответить еще на последний вопрос: мог ли приятель Шарадека так изменить массу m1 и m2 двух монет (оставляя остальным монетам их массу m), чтобы сделать невозможным обнаружение обмана. Если
m1≠m, m2≠m, m1≤m2
(что можно предположить), то возможен один из трех случаев;
I. m<m1≤m2, II. m1<m<m2, III. m1≤m2<m.
Теперь достаточно соответственно обозначить монеты с массой m1 и m2 через W и Y, или же через D и Y, или же через W и Y, чтобы результат взвешивания был следующий: -+- или +-+. Приятель Шарадека, следовательно, не мог так изменить массу монет, чтобы - быть полностью уверенным в том, что проведет мастера, хотя обнаружение подвоха зависит от того, обозначил ли мастер монеты буквами именно так, как следует, в чем мастер также не может быть уверен.
Рис. 168
96б. Нижний слой показан на рис. 168. Каждый другой слой получаем, перемещая в предыдущем слое первый столбец на правый край. Условие задачи, очевидно, выполняется.
97. Требуемое общество будет сконструировано, если мы посадим каждого из 12 не знакомых друг с другом лиц, на "свою" грань правильного додекаэдра " потребуем, чтобы каждый познакомился своими "соседями", т. е. с обитателями смежных граней.
Условие е) здесь соблюдается, как два лица, занимающие противоположные грани додекаэдра, не имеют общих соседей.
Общество, описанное доктором фадеком, также населяет грани правильного додекаэдра, но в этом случае нужно поступить обратным образом, а именно, познакомить каждого человека со всеми лицами, не являющимися его соседями.
Доктор Шарадек прав. Действительно, предположим обратное, т. е. то в определенный момент в правой половине находятся только две костяшки или еще меньше (рис. 169). После промежутка времени, который необходим каждой костяшке для перемещения по всей проволоке, расположение костяшек будет симметричным предыдущему (рис. 170): в левой половине счетов будут находиться две костяшки (или меньше), а в правой - восемь костяшек (или больше), что противоречит условию задачи.
Рис. 169
Рис. 170
99. Решение доктора Шарадека является удачным, независимо от того, где он живет. Действительно, рис. 171 показывает, как можно объехать все улицы города и вернуться к произвольно выбранной точке выезда. Длина кратчайшего объезда превышает на 16,7% длину всех улиц города.
Рис. 171
100. Пять городов Шалон, Витри, Шомон, Сэн-Кантэн и Реймс образуют замкнутый пятиугольник; одна из его сторон (сторона Шомон-Сэн-Кантэн) является суммой четырех остальных, ибо 236=86+40+30+80. Это возможно только тогда, когда вершины пятиугольника лежат на одной прямой. Города расположены на прямой в следующем порядке: Сэн-Кантэн, Реймс, Шалон, Витри и Шомон. Расстояние между Реймсом и Шомоном, следовательно, равно 40+30+80=150 км.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'