Глава 3. Пространство, многогранники, шары

29. Деление пространства

Через фиксированную точку пространства проводим плоскости так, чтобы разделить пространство на возможно большее число частей. Одна плоскость разделит пространство на две части, две пересекающиеся плоскости - на четыре части, три пересекающиеся в некоторой точке плоскости и не имеющие другой общей точки делят пространство на восемь частей. Какое максимальное число частей можно получить при четырех плоскостях? А какое - при n плоскостях?

30. Две проекции

Представим себе плоскость П₁ касательную к земному шару в Северном полюсе N, и плоскость П₂, касательную к земному шару в Южном полюсе S. Можно начертить одну карту, проектируя каждую точку на поверхности земли из N на П₂, и другую карту, проектируя каждую точку из S на П₁ это - так называемая стереографическая проекция. Теперь мы можем сложить обе плоскости так, чтобы меридианы сошлись. Каждой точке одной карты отвечает определенная точка другой карты, значит, мы определили некоторое отображение плоскости на себя. Как непосредственно определить это отображение?

31. Куб

Держа в руке модель куба так, чтобы он мог вращаться вокруг своей самой длинной оси (т. е. вокруг прямой, соединяющей противоположные вершины), можно намотать на него без просветов черную пряжу. Пряжа заштрихует только половину куба (почему?). То же самое можно проделать с другой осью; их всего четыре, и каждый раз мы используем другой цвет пряжи (черный, красный, голубой и желтый). Вся модель будет покрыта разными цветами, а из их смешения возникнут смешанные цвета (модель куба белая и этого цвета мы не учитываем). Сколько будет цветовых оттенков на кубе и каких?

32. Геодезические

Эта задача не требует знания математики. Наложим на неподвижный куб резинку (так называемую "рецептную", используемую в аптеках для упаковки лекарств) таким образом, чтобы она держалась на кубе и не пересекала сама себя. Линию, по которой уложится эта резинка, мы называем геодезической линией.

1. Сколько раз все геодезические линии покроют поверхность куба (т. е. сколько геодезических линий пройдет через каждую точку поверхности куба)?

2. Сколько имеется различных семейств геодезических линий, покрывающих поверхность куба?

33. Движение молекулы

Внутри кубической коробки движется без воздействия внешних сил материальная частица, которая отражается от стен коробки, согласно классическому закону (угол падения равен углу отражения, т. е. перпендикуляр к грани в точке отражения есть биссектриса угла, образованного прямой, по которой молекула прибывает, и прямой, по которой она удаляется). Возможно ли, чтобы молекула беспрестанно двигалась по замкнутому шестиугольнику, поочередно ударяясь при каждом обходе обо все стороны коробки? Определить точки отражений и проверить, заузлен ли полученный шестиугольник или нет.

34. Развертка куба

Модели многогранников делаются из плоских разверток. В развертке грани прилегают друг к другу ребрами, а модель строится путем загибания картонной развертки вдоль ребер. Таких различных разверток правильный тетраэдр имеет две. Сколько их имеет куб?

35. Кубы

Как известно, все пространство можно заполнить равными кубами. В каждой вершине будет сходиться восемь кубов. Поэтому можно - путем соответствующего отсечения вершин у кубов и склейки смежных отсеченных частей в одно тело - заполнить пространство правильными октаэдрами (восьмигранниками) и телами, оставшимися от кубов. Какие это будут тела? Если мы максимально возможно увеличим октаэдры, то какую часть пространства они займут?

36. Гексаэдр

Существует ли отличный от куба гексаэдр (шестигранник), все грани которого являются конгруэнтными ромбами?

37. Тетраэдр

Имеются 6 стержней различной длины, причем известно, что при любом их упорядочении из них можно составить тетраэдр (треугольную пирамиду). Сколько различных тетраэдров при этом может получиться?

38. Тетраэдр с конгруэнтными гранями

Можно ли построить треугольную пирамиду (тетраэдр), все грани которой являются конгруэнтными треугольниками с произвольно заданными длинами а, b, с сторон?

Если это возможно, то каков объем этого тетраэдра?

39. Октаэдр

Можно ли построить восьмигранник (октаэдр), все грани которого являются конгруэнтными четырехугольниками? Можно ли построить десятигранник (декаэдр) и, общее, 2n-гранник (где n > 3-произвольное целое число), обладающий тем же свойством?

40. Расстояние на поверхности

Сопоставим каждой паре точек замкнутой выпуклой поверхности кратчайшую из соединяющих их дуг (не исключено, что такая дуга не единственная, например, для любой пары диаметрально противоположных точек сферы существует бесконечно много кратчайших дуг). Расстоянием между точками А к В на поверхности назовем длину кратчайшей дуги АВ. Теперь мы можем говорить про расстояние РХ между Р и произвольной точкой X нашей поверхности. Для каждой точки Р можно найти самую дальнюю от нее точку Q поверхности (такая точка также может быть не единственной). Пример со сферой может создать впечатление, что для подобной пары точек PQ всегда имеются по крайней мере две соединяющие их кратчайшие дуги. Показать, что для некоторого тетраэдра это утверждение неверно.

41. Путешествие мухи

Муха седа на вершину модели правильного додекаэдра (двенадцатигранника) и решила обойти его, двигаясь по ребрам додекаэдра; при этом ей удалось посетить все вершины, не побывав ни в одной из них дважды и вернувшись в конце путешествия в исходную вершину. После этого она попробовала обойти тем же способом все вершины ромбического додекаэдра, ограниченного 12 ромбами (рис. 1). Удалось ли ей это?

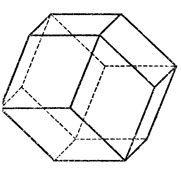
Рис. 1

42. Правильный додекаэдр

Грани правильного додекаэдра (двенадцатигранника) можно раскрасить в четыре цвета так, чтобы каждые две смежные грани были разных цветов. Доказать, что существуют всего четыре способа решения этой задачи, если условиться считать одним решением две раскраски, которые можно получить одну из другой вращением додекаэдра.

42а. Вписанный многогранник

В правильный додекаэдр можно вписать куб так, чтобы ребра куба являлись диагоналями правильных пятиугольников, служащих гранями додекаэдра. Это можно сделать несколькими способами; сколькими? Все эти кубы образуют звездчатый многогранник; каков объем полученного в объединении всех кубов многогранника, если объем додекаэдра равен 1?

Какое тело образует общая часть (пересечение) всех кубов?

43. Многогранник

Все грани выпуклого многогранника обязательно выпуклы. А обратно, обязательно ли является многогранник выпуклым, если все его грани - выпуклые многоугольники? В частности, существуют ли два многогранника (например, два тридцатигранника), ограниченных одинаковым числом попарно конгруэнтных граней (грани одного и того же тела не обязательно должны быть конгруэнтными между собой), из которых одно является выпуклым, а второе не является?

44. Не выпуклый многогранник

Может ли не выпуклый многогранник быть ограничен конгруэнтными четырехугольниками?

44а. Модели правильных многогранников

Из шести ребер правильного тетраэдра можно выбрать четыре ребра, образующих замкнутый косой, т. е. неплоский четырехугольник. Этот четырехугольник можно считать моделью тетраэдра, ибо он содержит все вершины тетраэдра. То же самое легко проделать с кубом; тогда мы получим (неплоский) восьмиугольник, содержащий все вершины куба. Можно ли этот прием распространить на другие правильные многогранники, т. е. на октаэдр, додекаэдр и икосаэдр? Сколько решений имеет задача?

45. Задача из Страны чудес

Люис Кэррол, математик и знаменитый детский писатель, был автором забавных нелепиц. Он советовал, например, пользоваться картой с масштабом 1:1, ибо достаточно разложить ее на земле, чтобы в любой момент знать, где находишься: надо просто прочитать надпись, на которой стоишь.

Представим себе, что, последовав этому совету, мы проведем на земном шаре прочной краской по суше и по морю меридианы и параллели и повсюду поместим каллиграфические названия городов, портов и стран. Компас станет излишним, но одна трудность все-таки останется: как отыскать кратчайший путь к избранной точке. Известно, что ортодромы, т. е. кратчайшие пути, не являются на этой карте Алисы из Страны чудес локсодромами, т. е. линиями, пересекающими меридианы (и параллели) под постоянным углом. Хуже всего то, что никакая перестройка координатных линий не поможет, ибо все системы координат будут обладать этим недостатком. Виноват в этом, конечно, земной шар, который так непрактично устроен. 4

Чтобы исправить нашу планету, лучше всего, конечно, начать с ее карты. Можно, например, начертить прямоугольную сеть параллелей и меридианов и свернуть карту в цилиндр так, чтобы параллели превратились в окружности. На такой цилиндрической планете кратчайший путь от одной точки к другой точке всегда пересекает меридианы под постоянным углом. Можно также разрезать карту вдоль параллели, обозначив на ней точку N, и свернуть ее в конус с вершиной в точке N. У конической планеты в точке N будет Северный полюс, параллели не будут пересекаться, исходящие из N меридианы тоже не будут, но каждая параллель пересечет каждый меридиан в двух точках, точно так же как и на земном шаре. И так же, как и раньше, кратчайший путь вновь будет иметь постоянное направление.

Но можно найти еще более интересную модель. На карте будет прямоугольная сеть координатных линий, но на планете появится только одно семейство линий: каждая линия пересечет любую другую в двух точках, а также и себя в одной точке. Принцип постоянного направления будет сохранен. Что это за модель?

Магистр Р. Новаковский, когда я ему рассказал об этих двух моделях, немедленно определил третью: прямоугольная сеть состоит из меридианов, параллелей и "посредников".

46. Три сферы и прямая

Три сферы имеют общую точку Р, причем известно, что никакая прямая, проходящая через точку Р, не касается сразу всех сфер. Показать, что эти сферы имеют еще одну общую точку.

47. Одно свойство сферы

Пусть известно, что все плоские сечения некоторой поверхности являются окружностями (точка рассматривается как окружность нулевого радиуса). Доказать, что эта поверхность является сферой.

47а. Укладывание шаров (I)

Имеем неограниченный запас одинаковых шаров. Уложим три из них так, чтобы все они соприкасались между собой, и затем присоединим четвертый шар так, чтобы он соприкасался с тремя первыми. Получим четыре гнезда, и в каждое из них можно вложить по одному шару. Теперь у нас уже восемь шаров. Сколько гнезд они образуют? Сколько теперь можно уложить шаров новым слоем? Можно ли продолжать этот процесс?

47б. Укладывание шаров (II)

У нас имеется неограниченный запас одинаковых шаров. Берем один из них и обкладываем его двенадцатью шарами, соприкасающимися с ним. Сколько будет теперь гнезд для последующих шаров? Можно ли в каждое гнездо уложить шар? Из скольких шаров будет состоять третий слой (первый состоит из одного, второй из 12 шаров)? Всегда ли мы сможем в последующих слоях заполнить все гнезда?