
Глава IV. Стохастическое программирование
§ 1. Предмет стохастического программирования
Оптимальные значения переменных (управлений) в задачах математического программирования являются функциями различных параметров, входящих в условие задачи (ресурсов, спроса, производительности труда и т. д.). Изменение одного или сразу нескольких параметров в свою очередь изменяет оптимальные значения некоторых или даже всех управляющих переменных. На практике же нередко встречаются такие задачи планирования, в которых значения параметров по самой своей природе являются случайными, т. е. непредсказуемыми заранее, а определяемыми лишь посредством вероятностных характеристик. Для того чтобы представить, насколько чувствительно оптимальное поведение к изменению этих параметров, необходимо было бы получить зависимости изменений управляющих переменных от всех случайных параметров. Однако для большинства задач это оказывается практически невозможно сделать из-за громадного объема вычислений.
В некоторых случаях при решении задач со случайными параметрами (в дальнейшем будем называть эти задачи (стохастическими задачами) можно использовать следующий прием: случайные величины еще до начала решения задачи заменяются усредненными значениями. Однако такой прием, означающий, что случайный процесс заменяется его детерминированной моделью, оказывается применим далеко не всегда. Он дает хорошие результаты только тогда, когда рассматриваемая система состоит из достаточно многочисленных объектов и когда случайные отклонения каждого из них взаимно компенсируются.
Принятый подход к решению стохастических задач состоит в том, что оптимизируется не сама функция цели, а ее математическое ожидание.
Понятие математического ожидания M (X) непрерывной случайной величины X вводится в теории вероятностей с помощью другого понятия - плотности вероятности φ (x) в данной точке x и определяется следующей формулой:
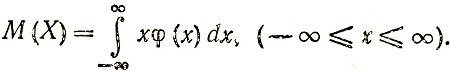
(4.1)
Для того чтобы показать смысл этой формулы, кратко напомним некоторые сведения из теории вероятностей, Обозначим вероятность P того, что значение непрерывной случайной величины X попадает в интервал значений от x до x+Δx следующим образом
P(x≤X≤x+Δx) = ΔF(x).
Тогда вероятность попадания X в интервал единичной длины есть
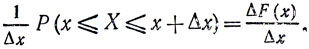
Величина 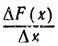 называется средней плотностью вероятности на интервале (x, x+Δx). Плотностью вероятности в точке x называется предельное значение средней плотности вероятности при Δx→0;
называется средней плотностью вероятности на интервале (x, x+Δx). Плотностью вероятности в точке x называется предельное значение средней плотности вероятности при Δx→0;
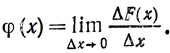
График функции φ (x) называется кривой распределения вероятности, а сама вероятность P (x1≤X≤x2) численно равна площади, ограниченной этим графиком, осью абсцисс и прямыми x = x1 и x = x2 т. е.
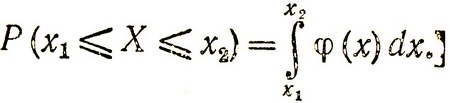
(4.2)
При x1→∞ и x2→∞ имеем
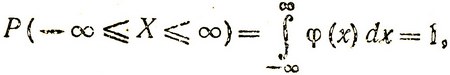
т. е, плотность вероятности φ(x) является нормированной на единицу.
Математическое ожидание (4.1) вводится по аналогии со средним арифметическим 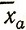 случайной дискретной величины x:
случайной дискретной величины x:
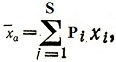
где xi - дискретные значения случайной величины, pi - вероятности их появления при испытаниях. Вероятность появления непрерывной величины x есть Φ (x)dx; суммирование заменяется интегрирование по всем возможным значениям x. Таким образом, математическое ожидание M (X) есть среднее значение непрерывной случайной величины X.
Исследование задач математического программирования со случайными параметрами (стохастических задач) составляет предмет стохастического программирования. Причем основным подходом к решению в стохастическом программировании является представление задачи в таком виде, чтобы ее можно было решить уже рассмотренными нами методами нелинейного (выпуклого) или динамического программирования. Поэтому все задачи, в которых некоторые параметры могут быть случайными величинами, удобно сразу разбить на два основных класса: одношаговых и многошаговых задач.
Начнем изучение стохастического программирования с рассмотрения одношаговых стохастических задач.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'