Глава 32. Квадрирование квадрата

Можно ли разрезать квадрат на меньшие квадраты так, что среди последних никакие два не будут одинаковыми? Долгое время считали, что эта чрезвычайно трудная математическая задача неразрешима. Преодолеть все трудности удалось лишь после того, как задача была переведена на язык теории электрических цепей, а затем снова на язык геометрии плоских фигур. Ниже мы приводим увлекательный рассказ профессора математики университета в Торонто Уильяма Т. Татта о том, как ему и трем его товарищам по Кембриджскому университету удалось в конце концов проквадрировать квадрат.

Это рассказ о математическом исследовании, проведенном в 1936-1938 годах четырьмя студентами Тринити-колледжа Кембриджского университета. Одним из них был автор этой статьи. Другим - К. А. Б. Смит, ныне занимающийся статистическими проблемами генетики в Лондонском университете. Смит также известен как автор многих статей по теории игр и задаче об отыскании фальшивой монеты среди заданного набора монет. Третьим участником был А. Г. Стоун, один из изобретателей флексагонов, ныне работающий в Манчестере над исследованием труднодоступных областей теоретико-множественной топологии. Четвертым был Р. Л. Брукс. В настоящее время он оставил академическую деятельность и перешел на государственную службу, но по-прежнему верен своему увлечению математическими головоломками. Свидетельство тому важная теорема из теории раскраски графов, носящая его имя. С присущей им скромностью эти четверо студентов называли себя не иначе как "выдающимися членами" Математического общества Тринити-колледжа.

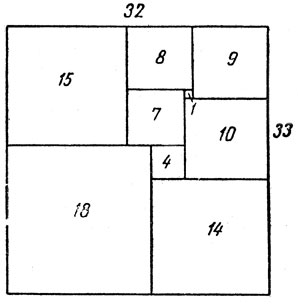
Рис. 159

В 1936 году литература по задаче о разрезании прямоугольника на неповторяющиеся квадраты была крайне бедна. Так, было известно, что прямоугольник со сторонами 32 и 33 единицы можно разрезать на девять квадратов со сторонами 1, 4, 7, 8, 9, 10, 14, 15 и 18 единиц (рис. 159). Стоуна заинтересовало высказанное в "Кентерберийских головоломках" Дьюдени предположение о том, что квадрат нельзя разрезать на неповторяющиеся квадраты. Из чистого любопытства он попытался найти доказательство этой гипотезы, но безуспешно, однако ему удалось найти разбиение прямоугольника со сторонами 176 и 177 единиц на 11 неповторяющихся квадратов (рис. 160 внизу).

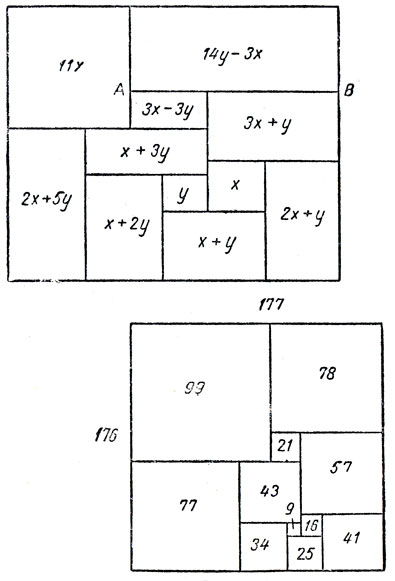
Рис. 160

Достигнутый успех, хотя он и не был полным, окрылил воображение Стоуна и трех его друзей, и вскоре мы всерьез увлеклись задачей и стали уделять ей много времени. Была разработана специальная терминология. Прямоугольник, который можно разрезать на неповторяющиеся квадраты, мы назвали "совершенным" прямоугольником. Позднее для обозначения прямоугольника, который допускает разрезание на два или большее число квадратов, не обязательно разных, нами был предложен термин "квадрируемый" прямоугольник.

Оказалось, что построить совершенный прямоугольник крайне просто. Метод построения заключается в следующем. Нарисуем прямоугольник, разрезанный на меньшие прямоугольники (рис. 160, вверху), и рассмотрим получившийся рисунок как искаженное изображение некоторого квадрируемого прямоугольника. Предположив, что меньшие прямоугольники на самом деле являются квадратами, мы с помощью несложных алгебраических выкладок найдем, какими должны быть длины сторон этих квадратов, чтобы сделанное предположение было верным. Рассмотрим, например, прямоугольник, изображенный в верхней части рис. 160. Обозначив стороны двух смежных квадратов через x и y, мы сразу же получим, что длина стороны примыкающего к ним снизу квадрата равна х + y, а сторона квадрата, примыкающего слева к квадратам со сторонами y и х + y, равна х + 2y и т. д. Продолжая этот процесс, мы получим показанные на рис. 160 формулы, выражающие длины сторон всех 11 квадратов, на которые был разрезан исходный прямоугольник. Наши формулы обеспечивают плотное (то есть без просветов и наложений) прилегание квадратов друг к другу всюду, кроме отрезка АВ. Выбирая х и y так, чтобы они удовлетворяли уравнению (3x + y) + (3x - 3y) - (14y - 3x), или 16y = 9х, можно добиться плотного прилегания квадратов, граничащих и по отрезку АВ. Полагая x = 16, y = 9 (эта пара значений х и y удовлетворяет только что выписанному уравнению), мы получаем совершенный прямоугольник, показанный на рис. 160 внизу, который был впервые найден Стоуном.

Иногда длины сторон квадратов, вычисленные по этому методу, оказывались отрицательными. Однако, как выяснилось, такие "отрицательные" квадраты небольшим изменением исходного рисунка всегда можно превратить в "положительные", поэтому никаких особых неприятностей при появлении "отрицательных" квадратов у нас не возникало. В некоторых более сложных случаях за неизвестные необходимо было принимать длины х, y и z сторон трех квадратов, тогда после всех алгебраических преобразований приходилось решать не одно, а два линейных уравнения. Иногда квадрируемый прямоугольник не приводился к совершенному, в этом случае мы считали попытку неудачной. К счастью, это случалось не слишком часто. Мы включали в свой каталог лишь "простые" совершенные прямоугольники, то есть совершенные прямоугольники, не содержащие других совершенных прямоугольников. Например, совершенный прямоугольник, получающийся из изображенного на рис. 159 квадрата путем пристраивания к нему сверху квадрата со стороной 32 единицы, не будет простым, и мы не включили его в свой список.

На первом этапе нашего исследования нами было построено много совершенных квадратов, допускавших разбиение на квадраты, число которых было различным: от 9 до 26. Окончательной, или канонической, формой прямоугольника мы считали такую, в которой длины сторон составляющих прямоугольник квадратов выражались взаимно простыми целыми числами. Мы надеялись, что, построив достаточно много совершенных прямоугольников, в конце концов сможем найти "совершенный квадрат". Однако по мере того, как удлинялся список совершенных прямоугольников, начала таять наша надежда, а вместе с ней пошла на убыль и наша производительность.

Рассматривая составленный нами каталог совершенных прямоугольников, мы заметили некоторые странные закономерности. Прямоугольники мы классифицировали по их "порядку", то есть по числу тех квадратов, из которых они составлены. Оказалось, что среди чисел, выражающих длины сторон квадратов, образующих прямоугольники данного порядка, заметна тенденция к повторению. Кроме того, полупериметр прямоугольника одного порядка часто по нескольку раз повторялся как длина стороны прямоугольника следующего порядка. Например, воспользовавшись всем, что уже говорилось о построении совершенных прямоугольников, нетрудно показать, что четыре из шести простых совершенных прямоугольников десятого порядка имеют полупериметр, равный 209, и что пять из 22 простых совершенных прямоугольников одиннадцатого порядка имеют сторону длиной 209 единиц. Мы много обсуждали это явление, названное нами "таинственным рекуррентным законом", но так и не смогли дать ему сколько-нибудь удовлетворительного объяснения.

На следующем этапе исследования было решено отказаться от эксперимента в пользу теории. Мы попробовали изображать квадрируемые прямоугольники различными диаграммами, но без особого успеха. Существенный прогресс был достигнут лишь после того, как Смит предложил особую разновидность диаграмм, названную в его честь остальными исследователями диаграммами Смита. Смит возражал против такого названия, мотивируя это тем, что предложенные им диаграммы являются всего лишь небольшой модификацией ранее известных. Как бы то ни было, диаграммы Смита неожиданно превратили нашу задачу в часть общей теории электрических цепей.

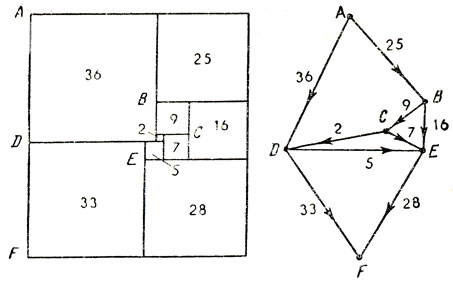
Рис. 161

На рис. 161 рядом с совершенным прямоугольником показана его диаграмма - диаграмма Смита. Каждому горизонтальному отрезку на схеме разбиения прямоугольника на квадраты мы сопоставили точку, или "клемму", на диаграмме Смита. "Клемма" лежит на продолжении соответствующей ей горизонтальной линии за контур прямоугольника вправо. Так, любой из входящих в разбиение квадратов ограничен сверху и снизу двумя горизонтальными отрезками, на диаграмме Смита его изображением служит линия, или "проводник", соединяющая две точки, одна из которых является изображением верхней стороны квадрата, а другая - изображением его основания. Представим себе, что по каждому проводнику течет ток. Пусть сила тока численно равна длине стороны квадрата, условно изображенного на диаграмме Смита данным проводником. Предположим, что ток идет в направлении от точки, соответствующей верхней стороне квадрата, к точке, сопоставленной основанию того же квадрата.

"Клеммы", отвечающие на диаграмме Смита верхней и нижней (горизонтальной) стороне большого прямоугольника, удобнее всего назвать положительным и отрицательным полюсами получившейся электрической цепи.

К нашему удивлению, выяснилось, что электрические токи, введенные по только что перечисленным правилам, ведут себя как "настоящие": они подчиняются правилам Кирхгофа для токов в цепи, если считать сопротивление каждого проводника равным единице. Первое правило Кирхгофа состоит в том, что алгебраическая сумма токов, входящих и выходящих из любого узла (из любой "клеммы"), кроме полюсов, равна нулю. Это означает, что сумма сторон квадратов, органиченных снизу данным горизонтальным отрезком, равна сумме сторон квадратов, ограниченных тем же отрезком сверху, если этот отрезок не принадлежит ни одной из горизонтальных сторон большого прямоугольника. Второе правило Кирхгофа гласит: алгебраическая сумма падений напряжения для любого замкнутого контура равна нулю. Наша цепь собрана из проводников с единичным сопротивлением, поэтому второе правило Кирхгофа применительно к нашему случаю можно сформулировать иначе: алгебраическая сумма токов для любого замкнутого контура в цепи равна нулю. Это означает, что если на схеме разбиения совершенного прямоугольника на квадраты выбрать произвольный замкнутый маршрут, то, обойдя его и вернувшись в исходную точку, мы пройдем вверх и вниз одинаковые расстояния.

Полный ток, втекающий в цепь из положительного полюса и вытекающий из цепи в отрицательный полюс, равен, очевидно, длине горизонтальной стороны прямоугольника, а разность потенциалов между двумя полюсами - длине вертикальной стороны прямоугольника.

Для нас открытие такой электрической аналогии было важно в том отношении, что позволяло связать нашу задачу с хорошо разработанной теорией. С помощью методов, заимствованных из теории электрических цепей, мы смогли получить формулы для токов в общей диаграмме Смита и, следовательно, для длин сторон квадратов, на которые разбивается квадрируемый прямоугольник. Главные результаты такого заимствования можно сформулировать так. С каждой электрической цепью можно связать определенное число, характеризующее ее структуру и не зависящее от того, какая именно пара узлов выбрана в качестве полюсов. Это число мы назвали сложностью цепи. Если единица длины для данного прямоугольника выбрана так, что длина его горизонтальной стороны численно равна сложности, то стороны составляющих его квадратов будут выражаться целыми числами. Кроме того, длина вертикальной стороны прямоугольника равна сложности другой цепи, которая получается из первой при слиянии обоих полюсов в одну точку.

Числа, задающие в такой системе единиц длины сторон прямоугольника и составляющих его квадратов, мы назвали "полными" длинами сторон и "полными" элементами прямоугольника соответственно. У некоторых прямоугольников полные элементы имеют общий множитель, больший единицы. Разделив в таком случае на общий множитель, мы получим "приведенные" длины сторон и элементы. Именно эти приведенные стороны и элементы мы включали в наш каталог.

Из полученных результатов было ясно, что если два квадрируемых прямоугольника отвечают электрическим цепям одинаковой структуры, отличающимся лишь выбором полюсов, то полные горизонтальные стороны таких прямоугольников равны. Если же структура электрических цепей двух прямоугольников совпадает лишь после совмещения в каждой из них обоих полюсов в одну точку, то у таких двух прямоугольников равны полные вертикальные стороны. Эти два факта объясняют все случаи того "таинственного рекуррентного закона", с которым мы сталкивались ранее.

Открытие диаграммы Смита упростило процесс получения и классификации простых квадрируемых прямоугольников. Без особого труда мы перечислили все допустимые электрические цепи, состоящие из не более чем 11 проводников, и нашли все соответствующие им квадрируемые прямоугольники. Затем мы обнаружили, что совершенных прямоугольников ниже девятого порядка не существует и что имеется лишь два совершенных прямоугольника девятого порядка (рис. 159 и 161). Были найдены все совершенные прямоугольники десятого (их оказалось 6) и одиннадцатого (их было 22) порядков. Затем, уже не столь быстро, нам удалось еще больше расширить наш каталог и включить в него совершенные прямоугольники двенадцатого (их мы насчитали 67) и тринадцатого порядков.

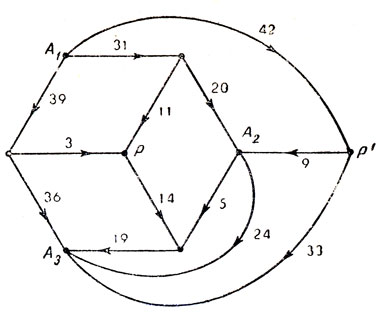
Рис. 162

Особенно приятно было вычислять совершенные прямоугольники, соответствующие цепям с высокой симметрией. Мы рассмотрели, например, цепь, образуемую ребрами проволочного куба с полюсами в двух его вершинах. Такая цепь не позволяет получить ни одного совершенного прямоугольника, однако если ее усложнить, включив в одну из граней куба диагональ, и расправить всю цепь, уложив ее на плоскость, то получится диаграмма Смита, изображенная на рис. 162. Ей соответствует совершенный прямоугольник, показанный на рис. 163. Этот прямоугольник особенно интересен тем, что его приведенные элементы необычно малы для тринадцатого порядка. Общий множитель полных элементов равен 6. Бруксу этот прямоугольник так понравился, что он решил сделать из него головоломку и разрезал на отдельные квадраты, которые нужно было складывать снова в прямоугольник.

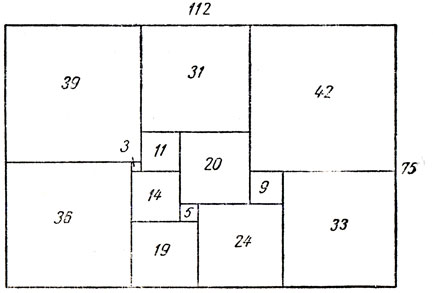
Рис. 163

Именно на этом этапе исследования мать Брукса и сделала открытие, которое послужило ключом к решению всей задачи. Она долго билась над разгадкой придуманной Бруксом головоломки, и в конце концов ей удалось сложить квадраты так, что они образовали прямоугольник. Но это был совсем не тот квадрируемый прямоугольник, который разрезал Брукс! Брукс поспешил вернуться в Кембридж, чтобы сообщить о существовании двух различных совершенных прямоугольников с одинаковыми приведенными сторонами и одинаковыми приведенными элементами. Перед нами снова была необъяснимая рекуррентная последовательность, да еще какая! "Выдающиеся члены" Математического общества Тринити-колледжа собрались на "внеочередное заседание.

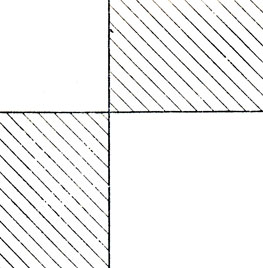
Рис. 164

Нам и раньше приходил в голову вопрос, могут ли различные совершенные прямоугольники иметь одинаковую форму. Нам хотелось получить два таких прямоугольника, не имеющих общих приведенных элементов, и таким образом построить совершенный квадрат. Идея построения ясна из рис. 164: две заштрихованные области означают два совершенных прямоугольника; добавив к ним два неравных между собой квадрата, мы могли бы получить большой совершенный квадрат. Но прямоугольники одинаковой формы до того времени не появились в нашем каталоге, и нам ничего не оставалось, как высказать сомнение в возможности существования таких прямоугольников. Открытие миссис Брукс, несмотря на то что ее прямоугольники имели одинаковые приведенные элементы и были, таким образом, весьма далеки от нашего идеала (прямоугольников одинаковой формы, не имеющих общих приведенных элементов), вновь возродило наши надежды.

На чрезвычайном заседании было много горячих споров. Однако лишь после того, как "выдающиеся члены" Математического общества Тринити-колледжа остыли настолько, что смогли начертить диаграммы Смита для исходного и найденного миссис Брукс прямоугольников, им стала ясна связь между тем и другим прямоугольником.

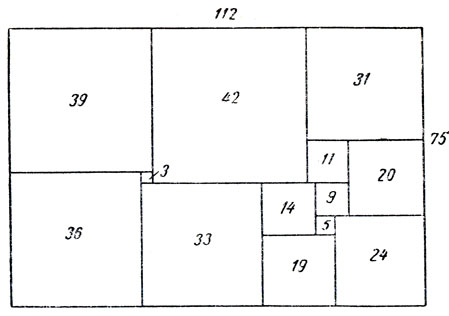
Рис. 165

Второй прямоугольник показан на рис. 165, а его диаграмма Смита - на рис. 166. Ясно, что если в цепи, изображенной на рис. 162, отождествить узлы Р и Р', то она перейдет в цепь, которая изображена на рис. 166. Поскольку электрический потенциал в точках Р и Р' на рис. 162 одинаков, отождествление точек Р и Р' не вызовет никаких изменений ни в токах, текущих по отдельным ветвям цепи, ни в полном токе, ни в разности потенциалов между полюсами. Так мы получили простое электрическое объяснение того факта, что два прямоугольника имеют одинаковые приведенные стороны и одинаковые приведенные элементы.

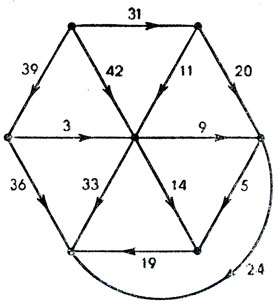
Рис. 166

Почему потенциалы в точках Р и Р' на рис. 162 одинаковы? Ответ на этот вопрос также был найден до закрытия чрезвычайного заседания. Для объяснения равенства потенциалов в точках Р и Р' достаточно заметить, что всю цепь можно разбить на три части, которые пересекаются только в полюсах А₁ и А₂ и узле A₃. Одна из этих частей состоит из одного проводника, соединяющего А₂ и A₃. Вторую часть образуют три проводника, сходящиеся в точке Р', а третья состоит из остальных девяти проводников. Третья частью обладает вращательной симметрией: точка A служит центром симметрии третьего порядка. Кроме того, токи могут входить в эту часть цепи и выходить из нее только через точки A₁, A₂ и A₃, эквивалентные относительно поворотов на 120°. Этого свойства третьей части цепи достаточно, чтобы утверждать, что потенциал в точке Р равен среднему арифметическому потенциалов, приложенных в точках A₁, A₂ и A₃, независимо от конкретных значений этих потенциалов. Проводя аналогичные рассуждения для точки Р, мы заключаем, что потенциал в точке Р' также должен быть равен среднему арифметическому потенциалов, приложенных в точках A₁, A₂ и A₃. Следовательно, потенциалы в Р и Р' равны независимо от того, какие потенциалы приложены в точках A₁, A₂ и A₃. В частности, они равны и тогда, когда полюсы цепи выбраны в точках А₁ и A₂, а величина потенциала в точке А₃ определяется правилами Кирхгофа.

Следующий шаг был случайно сделан автором этой статьи. Как мы только что видели, открытие миссис Брукс полностью объясняется простым свойством симметричных цепей. У меня возникла мысль, что свойствами симметрии можно воспользоваться для построения других примеров пар совершенных прямоугольников с одинаковым набором приведенных элементов. Я не мог объяснить, каким образом это может помочь нам в достижении главной цели или в доказательстве невозможности построения совершенного квадрата, но считал, что от новых идей не следует отказываться, прежде чем мы не выясним связанные с ними возможности.

Первое, что приходит в голову,- это заменить третью составную часть цепи на рис. 162 другой цепью, также обладающей вращательной симметрией третьего порядка относительно центрального узла. Произвести замену можно лишь при соблюдении весьма жестких условий, на объяснении которых необходимо остановиться подробнее.

Можно показать, что диаграмма Смита для квадрируемого прямоугольника всегда будет плоской. Это означает, что ее всегда можно начертить на плоскости так, что никакие два проводника не будут пересекаться нигде, кроме узлов. Кроме того, мы всегда можем добиться, чтобы на чертеже между полюсами не было ни одного замкнутого контура. Справедлива также и обратная теорема. Она утверждает, что любую электрическую цепь, на схеме которой нет ни пересечений отдельных ветвей, ни замкнутых контуров, разделяющих полюса цепи, можно рассматривать как диаграмму Смита некоторого квадрируемого прямоугольника. Я не буду останавливаться на строгом доказательстве этих теорем. Это заняло бы слишком много места, и, кроме того, у читателя создалось бы неверное представление о том, как был найден совершенный квадрат. В действительности же мы преспокойно обходились без строгих доказательств и занялись ими, лишь когда настало время приняться за подготовку статьи для печати.

Вряд ли можно приветствовать пренебрежение строгостью в математическом исследовании. Например, отказ от строгости в работе, целью которой является доказательство теоремы о четырех красках, привел бы (и уже неоднократно приводил) к самым печальным последствиям. Однако наше исследование в основном было экспериментальным, и его экспериментальными результатами были найденные нами совершенные прямоугольники. Временным обоснованием наших методов до того, как была разработана их точная теория, служили полученные с их помощью прямоугольники.

Однако вернемся к рисунку 162 и замене третьей компоненты цепи новой симметричной цепью с центром в точке Р. Полученная в результате такой замены цепь не только должна быть плоской, но и должна оставаться плоской при совмещении точек Р и Р'.

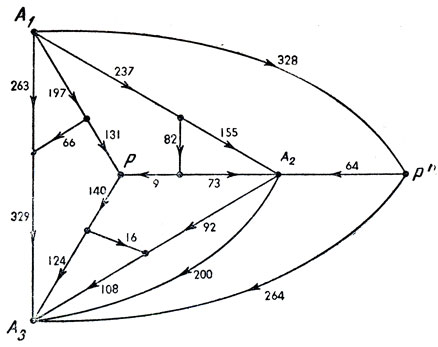
Рис. 167

После нескольких неудачных попыток я нашел две тесно связанные между собой цепи, удовлетворяющие этим условиям. Соответствующие диаграммы Смита показаны на рис. 167 и 168. Как и ожидалось, каждая диаграмма допускала отождествление точек Р и Р' и таким образом приводила к двум квадрируемым прямоугольникам с одинаковыми приведенными элементами. Неожиданным оказалось то, что у всех четырех прямоугольников одинаковые приведенные стороны.

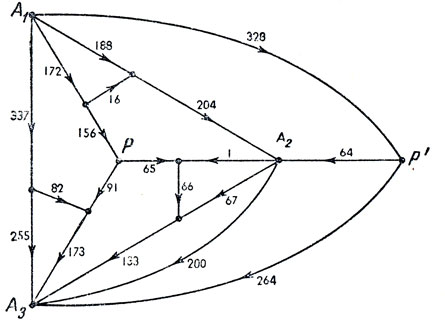
Рис. 168

По существу новое открытие означало, что прямоугольники, соответствующие диаграммам на рис. 167 и 168, имеют одинаковую форму, но их приведенные элементы совпадают не полностью. Вскоре было найдено простое теоретическое объяснение этого факта. Обе интересующие нас цепи одинаковы по структуре и различаются лишь положением полюсных узлов, поэтому у соответствующих им прямоугольников полные горизонтальные стороны равны. Кроме того, совместив полюса каждой из цепей, мы снова получим две неотличимые по своей структуре цепи. Это означает, что у соответствующих прямоугольников полные вертикальные стороны также равны. Все же нас не покидало ощущение, что найденное нами объяснение не слишком глубоко, поскольку оно никак не использует вращательную симметрию цепи.

В конце концов мы условились называть вновь открытое явление "эквивалентностью между ротором и статором". Оно всегда наблюдалось у цепей, которые можно было разбить на две части - "ротор" и "статор" - со следующими свойствами: ротор обладает вращательной симметрией; все узлы, общие для ротора и статора, эквивалентны относительно операций симметрии ротора, а полюса принадлежат статору. Например, на рис. 167 статор состоит из проводников, соединяющих узел Р' с точками А₁, А₂ и A₃, и проводника, соединяющего A₂ с А₃. Вторую цепь можно получить с помощью операции, называемой "обращением" ротора. Если схема цепи хорошо начерчена, то "обращению" ротора можно придать наглядный смысл: эта операция есть не что иное, как отражение ротора относительно прямой, проходящей через его центр. Так, отражая ротор цепи, изображенной на рис. 167, относительно прямой PA₃, мы получаем цепь на рис. 168.

Изучив несколько примеров эквивалентности между ротором и статором, мы убедились, что обращение ротора не изменяет полных сторон прямоугольника и токов в статоре, но токи в роторе могут изменяться. Удовлетворительные доказательства этих утверждений были получены гораздо позднее.

Эквивалентность между ротором и статором имеет лишь косвенное отношение к явлению, открытому миссис Брукс, и ее следует рассматривать просто как еще одно свойство цепей, имеющих симметричные части. Для нас важность сделанного миссис Брукс открытия заключалась в том, что оно подсказало нам мысль об исследовании таких цепей.

Теперь нас неотступно преследовал новый вопрос: каково наименьшее число общих элементов у совершенных прямоугольников, образующих пару ротор-статор? Прямоугольники на рис. 167 и 168 имеют семь общих элементов, из них три отвечают токам в роторе. Тот же ротор со статором, состоящим лишь из одного-единственного проводника А₂А₃, порождает два совершенных прямоугольника шестнадцатого порядка с четырьмя общими элементами. Возникла мысль: почему бы, используя статоры, состоящие только из одного проводника, не попытаться построить пару совершенных прямоугольников, имеющих лишь один общий элемент - тот, который соответствует статору? Теоретически никаких причин, которые бы препятствовали этому, не было. В то же время мы ясно сознавали, что если нам удастся построить пару таких прямоугольников, то мы смогли бы построить совершенный квадрат. Действительно, у роторов с вращательной симметрией третьего порядка, изучением которых мы занимались, статор, состоящий лишь из одного проводника, на схеме разбиения каждого прямоугольника на квадраты всегда изображается угловым элементом. Мы надеялись, что из двух совершенных прямоугольников с единственным общим угловым элементом нам удастся построить совершенный квадрат. Идея его построения ясна из рис. 169. Заштрихованные части означают совершенные прямоугольники; квадрат, в котором они перекрываются, соответствует их общему угловому элементу.

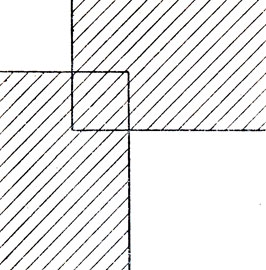
Рис. 169

Мы приступили к вычислению пар ротор - статор. Роторы мы выбирали как можно более простые, отчасти из желания облегчить свой труд, отчасти в надежде получить совершенный квадрат с небольшими приведенными элементами. Но наши построения одно за другим терпели неудачу, и мы впали было в отчаяние. Неужели путь к решению преграждает еще какой-то теоретический барьер, который также придется исследовать?

Кому-то из нас пришло в голову, что причина неудач могла крыться в излишней простоте конструкции наших роторов и что более сложные роторы, возможно, будут лучше: оперировать придется с гораздо большими числами и возможность случайного совпадения уменьшится. В один прекрасный день, придя в колледж, Смит и Стоун засели за расчет сложной пары ротор - статор, не зная о том, что Брукс, находившийся в другой комнате, также занят вычислением другой такой пары. Когда несколько часов спустя Смит и Стоун ворвались к Бруксу с криком: "Мы нашли совершенный квадрат!", тот уже мог ответить: "Я тоже!"

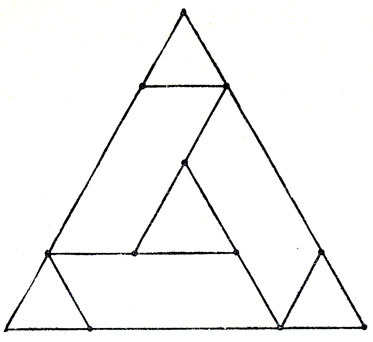
Рис. 170

Оба найденных квадрата были шестьдесят девятого порядка. Брукс, продолжая экспериментировать над не слишком сложными роторами, сумел получить совершенный квадрат тридцать девятого порядка, соответствующий ротору на рис. 170. Полное описание этого квадрата содержится в формуле: [2378, 1163, 1098], [65, 1033], [737, 491], [249, 242], [7/235], [478, 259], [256], [324, 944], [219, 296], [1030, 829, 519, 697], [620], [341, 178], [163, 712, 1564], [201, 440, 157, 31], [126, 409], [283], [1231], [992, 140], [852].

В этой формуле каждая пара скобок соответствует одному из горизонтальных отрезков на схеме разбиения совершенного квадрата. Горизонтальные отрезки берутся в том порядке, как они следуют по вертикали сверху вниз. Первым идет верхнее основание совершенного квадрата; его нижнее основание в перечислении горизонтальных отрезков не участвует. Числа в скобках означают длины сторон тех элементарных квадратов, чьи верхние основания принадлежат соответствующему горизонтальному отрезку; эти длины перечисляются по порядку, слева направо. Приведенная сторона совершенного квадрата равна сумме чисел, заключенных в первых скобках, то есть 4639.

Эти обозначения принадлежат К. И. Баувкампу. Он воспользовался ими при составлении своего списка простых квадрируемых прямоугольников до 13-го порядка включительно.

На этом по существу и заканчивается история о том, как наша четверка решила задачу о построении совершенного квадрата. Правда, мы продолжали работать над задачей и после того, как были получены первые положительные результаты. Дело в том, что все совершенные квадраты, полученные по методу ротора-статора, обладали некоторыми свойствами, которые мы считали их недостатками. Каждый из построенных нами квадратов содержал совершенный прямоугольник меньших размеров, то есть не был простым. Каждый из них имел внутри себя точку, которая принадлежала четырем элементарным квадратам одновременно, то есть была центром "креста", образованного сторонами этих квадратов. Наконец, каждый из построенных нами совершенных квадратов содержал элементарный квадрат, который, хотя и был отличен от четырех угловых элементарных квадратов, тем не менее делился диагональю большого квадрата пополам. Используя более тонкую теорию роторов, мы сумели построить совершенные квадраты, лишенные двух первых недостатков. И лишь несколькими годами позже с помощью метода, основанного на использовании симметрии совсем иного рода, я получил совершенный квадрат 69-го порядка, свободный от всех трех недостатков. Я не могу останавливаться здесь на изложении этой работы и вынужден отослать тех читателей, кого она заинтересует, к нашим специальным статьям.

В истории совершенного квадрата следует назвать еще три эпизода, хотя каждый из них знаменует не подъем, а спад в развитии теории.

Начнем с того, что мы не прекращали работы по составлению каталога совершенных прямоугольников 13-го порядка. Однажды мы обнаружили, что два из найденных прямоугольников имеют одинаковую форму, хотя все элементы у них различны. Это позволило нам построить совершенный квадрат 28-го порядка (идея его построения ясна из рис. 164). Позднее мы нашли совершенный прямоугольник 13-го порядка, который в комбинации с совершенным прямоугольником 12-го порядка и одним элементарным квадратом позволил нам построить совершенный квадрат 26-го порядка. Если о качестве совершенного квадрата судить по малости его порядка, то эмпирический метод составления каталога совершенных треугольников доказал свое превосходство над нашим изящным теоретическим методом.

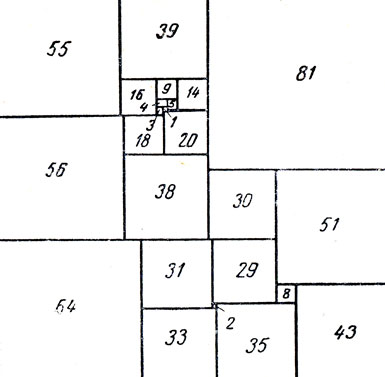
Рис. 171

Эмпирический метод позволил добиться замечательных результатов и другим исследователям. Р. Спрэг ухитрился сложить из элементарных квадратов совершенный квадрат 55-го порядка. Это был первый из опубликованных совершенных квадратов (1939 год). Позднее Т. Г. Уиллкокс, включивший в свой каталог не только простые, но и составные совершенные прямоугольники, нашел совершенный квадрат 24-го порядка (рис. 171). Его формула имеет следующий вид: [55, 39, 81], [16, 9, 14], [4, 5], [3, 1], [20], [56, 18], [38], [30, 51], [64, 31, 29], [8, 43], [2, 35], [33]. Этот совершенный квадрат и поныне держит рекорд малости порядка.

В отличие от теоретического метода эмпирический подход до сих пор еще не позволил построить ни одного простого совершенного квадрата.

На тот случай, если кому-нибудь из читателей захочется самому повозиться с совершенными прямоугольниками, приведу две нерешенные задачи. Первая заключается в том, чтобы найти наименьший возможный порядок совершенного квадрата, вторая - в том, чтобы построить простой совершенный прямоугольник, горизонтальная сторона которого вдвое больше вертикальной.

В 1960 году К. И. Баувкамп опубликовал каталог всех простых квадрируемых прямоугольников (то есть квадрируемых прямоугольников, не содержащих квадрируемых прямоугольников меньших размеров) до 15-го порядка включительно. С помощью электронной вычислительной машины Баувкамп и его сотрудники получили следующие результаты:

Несовершенными простыми квадрируемыми прямоугольниками здесь названы такие, которые содержат по крайней мере два одинаковых квадрата; совершенными - такие прямоугольники, в разбиение которых входят только неповторяющиеся квадраты. Общее число простых квадрируемых прямоугольников до 15-го порядка включительно равно 4094. Интересно отметить, что все простые квадрируемые прямоугольники 10-го и 11-го порядков одновременно являются и совершенными. Единственный несовершенный простой прямоугольник 9-го порядка имеет формулу: [6, 4, 5], [3, 1], [6], [5, 1], [4]. Он обладает приятной симметрией и может служить превосходной задачей на разрезание для детей.

Несколько квадрируемых прямоугольников было опубликовано в сборниках головоломок С. Лойда и Г. Дьюдени, но ни один из этих прямоугольников не был ни простым, ни совершенным. Пример простого, но не совершенного квадрируемого квадрата 26-го порядка приведен в книгах Г. Штейнгауза и М. Крайчика. Один из читателей прислал мне фотографию красивого внутреннего дворика прямоугольной формы, выложенного из 19 квадратных бетонных блоков с двухдюймовыми прокладками из красного дерева.

Наименьший из опубликованных квадратов, являющийся одновременно и простым и совершенным, построил Р. Л. Брукс. Это квадрат 38-го порядка со стороной 4920. В 1959 году результат Брукса был улучшен Т. Г. Уиллкоксом, который нашел квадрат 37-го порядка со стороной 1947.

Естественно, возникает вопрос о том, можно ли рассечь куб на конечное число меньших кубов так, чтобы все они были различных размеров. Оказывается, нет. Изящное доказательство этого факта было дано "выдающимися членами" Математического общества Тринити-колледжа^*. Ход доказательства примерно таков.

^* (R. L. Brooks, С. А. В. Smith, A. H. Stone, W. Т. Tulle, The Dissection of Rectangles into Squares, Duke Mathematical Journal 7, 1940, pp. 312-340.)

Представьте себе, что на столе перед вами стоит куб, разрезанный на кубики меньших размеров, причем среди кубиков нет двух одинаковых. Ясно, что нижняя грань куба представляет собой квадрируемый квадрат. Среди элементарных квадратов, входящих в разбиение нижней грани, найдется наименьший. Нетрудно видеть, что наименьший квадрат не может прилегать к стороне большого квадрата, то есть к ребру нижней грани куба. Поэтому наименьший из кубов, опирающихся на крышку стола,- назовем его куб А - должны окружать другие кубы. Ни один из этих окружающих кубов не может быть меньше куба А, поэтому их грани образуют вокруг него забор, высота которого превышает высоту куба А. Следовательно, на куб А может опираться лишь куб еще меньших размеров. На верхней грани куба А они порождают некий квадрируемый квадрат. Среди элементарных квадратов, на которые разлагается верхняя грань куба А, найдется наименьший квадрат. Обозначим через В наименьший из кубов, опирающихся на верхнюю грань куба А.

В свою очередь среди кубов, опирающихся на верхнюю грань куба В, найдется наименьший куб С. Итак, мы получаем бесконечную последовательность все меньших и меньших кубов, напоминающую известное шуточное стихотворение Свифта о блохах, которых кусают еще меньшие блошки, и т. д. до бесконечности. Следовательно, куб нельзя рассечь на конечное число неповторяющихся кубов меньших размеров.

"Гранями" четырехмерного гиперкуба служат обычные трехмерные кубы. Если "гиперкубировать" гиперкуб, то есть рассечь его на неповторяющиеся меньшие гиперкубы той же размерности, то его грани должны стать "кубированными" кубами. Поскольку, как мы только что видели, куб нельзя разрезать на неповторяющиеся меньшие кубики, "гиперкубирование" четырехмерного куба невозможно. Отсюда следует, что пятимерный куб также нельзя разбить на меньшие пятимерные кубы различных размеров. Продолжая по индукции, мы приходим к заключению, что аналогичный вывод остается в силе для гиперкубов любой размерности, большей двух.

Примером совершенного квадрируемого прямоугольника бесконечного порядка может служить прямоугольник, изображенный на рис. 128^*.

^* (На русском языке имеются две книги о разрезании квадратов: И. М. Яглом, Как разрезать квадрат?, М., изд-во "Наука", 1968 и Б. А. Кордемский, Н. В. Русалев, Удивительный квадрат, М., Гостехтеоретиздат, 1952.)