Глава 33. Механические головоломки

В отличие от занимательных задач, обычно решаемых с помощью карандаша и листка бумаги, механические головоломки требуют кое-какого специального "оборудования", реквизита и ловких рук. Этим "оборудованием" могут быть и самые обыкновенные кусочки картона, и замысловатые конструкции из дерева и металла, повторить которые по плечу далеко не каждому мастеру. Среди тех механических головоломок, которые иногда продаются в магазине игрушек, встречаются чрезвычайно интересные с математической точки зрения. По этой причине некоторые любители математических развлечений их коллекционируют. Самая большая из известных мне коллекций собрана Лестером А. Граймзом, инженером по технике противопожарной безопасности из Нью-Рошелла, штат Нью-Йорк. (Несколько менее обширная коллекция, в которой, однако, более полно представлены старинные игрушки XIX века и китайские головоломки, принадлежит Томасу Рэнсому из Белвилла, пров. Онтарио, Канада.) Коллекция Граймза насчитывает около 2000 разнообразнейших головоломок; среди них встречаются и подлинные шедевры и редкости. О головоломках из этой коллекции и пойдет в основном речь в этой главе.

Рис. 172. Лестер А. Граймз и некоторые из его 2000 механических головоломок

История головоломок еще не написана. Тем не менее вряд ли можно сомневаться в том, что древнейшей из них является старинная китайская игра танграм, известная в Китае под названием чи-чао-тю (что означает "хитроумный узор из семи частей"). В течение вот уже нескольких тысячелетий эта игра служит любимым развлечением в странах Востока, а с начала XIX века она получила распространение и на Западе. Рассказывают, что Наполеон, находясь в изгнании на острове Св. Елены, часами занимался составлением картинок из элементов танграма. Название "танграм" (неизвестное в Китае), по-видимому, было придумано в середине XIX века каким-то английским или американским "игрушечных дел" мастером, чье имя, к сожаленю, до нас не дошло.

Фигуркам, которые можно составить из семи элементов танграма, посвящено множество альбомов и книг^*. Среди них следует упомянуть и небольшую книжку знаменитого американского составителя головоломок Сэма Лойда, ныне ставшую библиографической редкостью и высоко ценимую знатоками.

^* (Много задач такого рода собрано в книге Я. И. Перельмана "Фигурки-головоломки из 7 кусочков", Л.- М., "Радуга", 1927. См. также книгу Б. А. Кордемского и Н. В. Русалева, о которой говорится в предыдущем примечании.- Прим. ред.)

Время от времени появлялись и другие головоломки, похожие на танграм (так, древние греки и римляне развлекались тем, что складывали фигурки из "обломков" разрезанного на 14 частей прямоугольника; изобретение этой игры приписывают Архимеду), но пережить танграм не суждено было ни одной из них. Чтобы понять причину удивительного,долголетия этой старинной китайской игры, достаточно определенным образом разрезать квадрат из плотного картона и испытать свое искусство в складывании уже известных и придумывании новых фигурок. Схема разрезания квадрата показана на рис. 173. Ту часть квадрата, которая имеет форму параллелограмма, следует окрасить в черный цвет с двух сторон, чтобы при желании ее можно было переворачивать на другую сторону. В каждой фигуре должны быть использованы все семь элементов танграма. Трудности, как правило, возникают лишь при составлении геометрических фигур. О том, какие изящные силуэты можно выложить из семи элементов танграма, вы можете судить по рис. 173.

Рис. 173. Китайский танграм (вверху слева) и некоторые из фигурок, которые можно составить из семи элементов - 'танов'

Простые головоломки, связанные с разрезанием фигур, иногда могут приводить к весьма нетривиальным математическим задачам. Предположим, например, что вы хотите найти все (различные) выпуклые многоугольники (многоугольник называется выпуклым, если все его внешние углы больше или равны 180°), которые можно составить из семи "танов". После длительного пользования методом проб и ошибок вам удастся найти некоторые из них, но как доказать, что вы нашли все выпуклые многоугольники? Два китайских математика, Фу Тренван и Чуань Чисюнь, в 1942 году опубликовали статью, в которой рассмотрели эту задачу. Их подход к решению был весьма остроумен. Каждую из пяти больших частей танграма (два больших треугольника, один треугольник поменьше, квадрат и параллелограмм); можно разбить на равнобедренные прямоугольные треугольники, конгруэнтные двум самым маленьким треугольникам танграма. Всего при этом получится 16 совершенно одинаковых равнобедренных прямоугольных треугольников. С помощью тонких рассуждений авторы показали, что из этих 16 треугольников можно построить 20 различных выпуклых многоугольников (многоугольники переходящие друг в друга при поворотах и отражениях, различными не считаются). Отсюда уже нетрудно доказать, что лишь 13 из найденных 20 выпуклых многоугольников можно построить из деталей танграма.

Среди 13 допустимых многоугольников имеется: один треугольник, шесть четырехугольников, два пятиугольника и четыре шестиугольника. Треугольник и три четырехугольника показаны на рис. 173. Приятной, но отнюдь не легкой задачей может служить отыскание девяти остальных выпуклых многоугольников. Каждый из них можно построить несколькими способами, но один из шестиугольников по трудности превосходит все 12 остальных фигур.

Другая широко распространенная разновидность головоломок, различные варианты которой встречались много веков назад,- игры с шашками или какими-нибудь заменяющими их предметами, которые для достижения того или иного результата необходимо передвигать по доске в соответствии с принятыми правилами. Одна из лучших головоломок этого типа, широко распространенная в Англии времен королевы Виктории, показана на рис. 174. Цель игры заключается в том, чтобы за наименьшее число ходов поменять местами черные и белые фишки. Ходом считается либо перемещение фишки из одного квадрата в соседний пустой квадрат, либо перепрыгивание через соседнюю фишку в пустой квадрат. Перепрыгивать можно через фишки как своего, так и другого цвета. Все фишки ходят, "как шахматная ладья", ходить по диагонали запрещается. В большинстве сборников головоломок приводится решение этой задачи в 52 хода, но известнейший английский специалист по головоломкам Генри Дьюдени нашел изящное решение в 46 ходов. Играть в эту игру можно маленькими фишками, помещая их прямо на рис. 174. Все квадраты пронумерованы, чтобы читателю легче было записывать ходы.

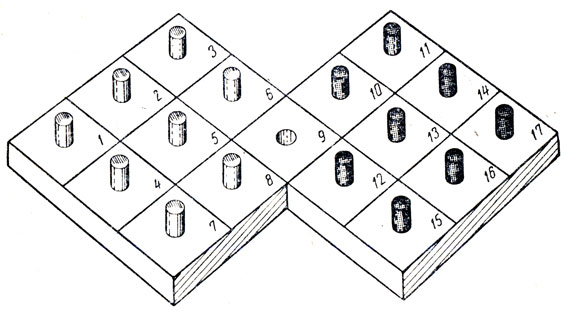
Рис. 174. Как поменять местами черные и белые фишки за наименьшее число ходов?

И танграм и головоломка с перестановкой фишек в некотором смысле являются приятными исключениями: их нетрудно построить самому. Большинство же головоломок в коллекции Граймза настолько сложны по своему устройству, что выполнить их возьмется далеко не каждый мастер. Полностью оценить их можно лишь тогда, когда у вас есть возможность подержать и повертеть их в своих руках, поэтому я ограничусь лишь кратким описанием этой разновидности головоломок. Сюда входят: шкатулки, кошельки, портсигары и всякого рода коробочки с потайными замками, которые вы должны найти и открыть; сотни головоломок из причудливо изогнутых проволочек, которые нужно расцепить; серебряные браслеты и кольца, составленные из отдельных хитроумно сцепленных между собой деталей; различные предметы, опутанные веревочками, которые нужно умудриться снять, не разрезая и не развязывая этих веревочек; игры, в которых вы должны проявить всю вашу ловкость и, встряхивая или острожно поворачивая коробочку закрытую сверху стеклом, загнать шарики или какие-нибудь другие мелкие предметы в то или иное положение; кольца, которые нужно снять с продетых в них стержней; головоломки типа Колумбова яйца; китайские головоломки, составленные из сцепленных между собой кусочков дерева самой замысловатой формы; игры с перекладыванием фигур и перестановкой фишек и сотни любопытнейших головоломок, не поддающихся никакой классификации. Кто изобретает такие игрушки? Проследить их происхождение до самых истоков - задача непосильная: во многих случаях нам неизвестно даже, в какой стране изобретена та или иная головоломка.

Однако и здесь имеется одно счастливое исключение. Особый раздел в коллекции Граймза занимают около 200 замечательных головоломок, изобретенных и сконструированных Л. Д. Уитткером, ветеринаром из Фармвиля, штат Виргиния. Все они искусно вырезаны из драгоценных пород дерева (Уитткер вытачивает их в мастерской, устроенной в подвале его дома), многие из них очень сложны и дьявольски остроумны. Как правило, головоломка имеет вид коробочки с отверстием в крышке. Бросив туда стальной шарик, вы должны выкатить его через другое отверстие в боковой стенке. Над коробочкой разрешается производить любые манипуляции, не ломая и не открывая ее. Разумеется, одними лишь постукиваниями по коробочке мы не сможем заставить шарик прокатиться по всем внутренним ходам и выйти наружу. Некоторые препятствия на своем пути он сможет преодолеть лишь в том случае, если мы догадаемся определенным образом встряхнуть коробочку. Другие барьеры с его пути можно убрать, если воспользоваться магнитом или подуть в специальную дырочку. Внутренние магниты размещены так, что они притягивают к себе шарик, удерживая его. Вы ничего не подозреваете об этом, потому что внутри коробки специально для того, чтобы ввести вас в заблуждение, положены "подставные" шарики, которые и будут греметь при встряхивании головоломки. Снаружи коробочки могут быть колесики, рычажки и кнопки самого различного вида. Манипулируя определенным образом некоторыми из них, вы можете помочь шарику выбраться наружу; некоторые же из них сделаны лишь для того, чтобы обмануть вас. Иногда для того, чтобы протолкнуть шарик через очередное препятствие, нужно ткнуть булавкой в незаметную на первый взгляд дырочку.

Несколько лет назад Граймз и Уитткер заключили между собой соглашение, по которому Граймз через определенный промежуток времени регулярно должен получать от Уитткера новую головоломку. Если Граймз успеет разгадать ее в течение месяца, то он вправе оставить новинку у себя безвозмездно; в противном случае он должен купить ее. Иногда стороны, не довольствуясь условиями соглашения, заключали еще и азартные пари. Как-то раз Граймз почти год безуспешно бился над разгадкой головоломки Уитткера, но все его усилия так и не привели к успеху. С помощью маленького компаса

Рис. 175. Чтобы разгадать одну из головоломок (на снимке - слева), Граймзу пришлось просветить ее рентгеновскими лучами

Граймз установил расположение внутренних магнитов, а изогнутыми проволочками обследовал все отверстия. Выходное отверстие было закрыто пробкой, которую нужно было протолкнуть внутрь, но что-то удерживало ее: по-видимому, расположенные внутри стальные шарики. Граймз догадался, что, наклонив определенным образом коробку, он сумеет выкатить шарики из-под пробки, но все его попытки оканчивались неудачей. В конце концов он просветил устройство рентгеновскими лучами (рис. 175) и решил головоломку. На рентгенограмме обнаружилась одна большая полость, в которую нужно было загнать пятый шарик. Когда все пять шариков заняли свои места, пробка поддалась.

Остальное было уже не так трудно, хотя один раз для выполнения сложного маневра потребовалось 3 руки: надавливая правой и левой рукой на определенные места футляра, нужно было еще поднять рычажок, удерживаемый сильной пружиной. Граймзу удалось проделать и этот трюк, привязав к рычажку нить, другой конец которой был прикреплен к его ноге!

При игре в танграм обычно труднее всего бывает построить изображенный на рис. 176 шестиугольник. Это самый сложный из всех 13 известных в танграме выпуклых многоугольников. Решение единственно с точностью до перестановки заштрихованных кусков фигуры.

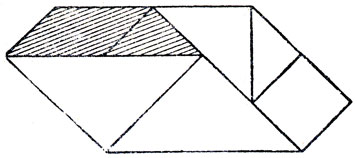
Рис. 176. Самый трудный из всех выпуклых многоугольников, который можно построить из семи элементов танграма

Решение задачи о перестановке черных и белых фишек в 46 ходов выглядит так:

После 23 ходов черные и белые фишки образуют на доске симметричный узор. Поэтому вторая половина ходов просто повторяет в обратном порядке ходы, сделанные в первой половине игры.

Возможны изящные решения в 46 ходов, отличные от решения Дьюдени. Один из читателей нашел 48 таких решений в 46 ходов, которые существенно отличались друг от друга.