Глава 31. Оригами [1971 Гарднер М. - Математические головоломки и развлечения]

Среди многих явлений японской культуры, вызывающих в последнее время все больший и больший интерес, следует назвать оригами - старинное японское искусство складывания различных фигурок из бумаги. В Англии вышло в свет несколько книг, посвященных оригами, в Манхэттене процветает руководимая миссис Гарри К. Оппенгеймер мастерская оригами, а в 1959 году в Нью-Йорке в помещении Музея Куперовского объединения декоративного искусства открылась первая в Соединенных Штатах выставка оригами.

Возникновение оригами теряется во мгле истории Древнего Востока. Сложенные из бумаги птички (их носили как украшения на кимоно) можно увидеть на японских гравюрах XVIII века, но само искусство оригами и в Китае, и в Японии зародилось на много столетий раньше. Было время, когда владение искусством оригами считалось обязательным для утонченных японских дам. Ныне в искусстве оригами практикуются лишь гейши и японские дети, которых знакомят с ним в школе. За последние 20 лет сильно возросла популярность оригами в Испании и Латинской Америке. В этом немалая заслуга выдающегося испанского поэта и философа Мигеля де Унамуно. Он не только написал пародийно-серьезный трактат по оригами, но и придумал особый способ складывания листа бумаги, позволивший ему создать много новых забавных фигурок.

Классическое оригами - это искусство складывать из одного лишь листа бумаги, без каких-либо разрезов, склеиваний или дорисовывания отдельных деталей, реалистические фигурки животных, птиц, рыб и других предметов. В современном оригами столь строгими требованиями иногда пренебрегают: там сделают небольшой надрез ножницами, здесь добавят капельку клея, карандашом подрисуют глазки и т. д. Но подобно тому как прелесть восточной поэзии заключена в полноте выражения мысли и чувства при минимальном числе слов и весьма жестких правилах стихосложения, точно так же и оригами привлекает нас необычайным реализмом своих произведений, хотя для создания их не требуется ничего, кроме квадратного листа бумаги и пары искусных рук. Листок бумаги, согнутый вдоль ничем не примечательных унылых геометрических линий, внезапно преображается, превращаясь на наших глазах в изящное миниатюрное произведение полуабстрактной скульптуры, поражающее нас своим совершенством.

Если принять во внимание геометрическую сторону складывания фигур из бумаги, то вряд ли кого-нибудь удивит, что многие математики с увлечением занимались этим прекрасным, таящим в себе неисчерпаемое разнообразие форм искусством. Так, одним из восторженных поклонников сложенных из бумаги фигурок был Льюис Кэррол, автор общеизвестных книг "Алиса в Стране Чудес" и "Алиса в Зазеркалье", преподававший математику в Оксфорде. (Записи в дневнике Кэррола свидетельствуют о том, какой восторг охватил его, когда пи научился складывать из бумаги игрушку, издававшую при сильном взмахе ею в воздухе громкий хлопок.) Складывание различных моделей из бумаги, в том числе и занимательных игрушек, известных под названием флексатонов (см. главу 17), занимает видное место в литературе по занимательной математике. Ему посвящено много брошюр и статей.

Уже самое простое перегибание листа бумаги приводит к интересному математическому вопросу. Почему, когда мы перегибаем лист бумаги, линия сгиба является прямой? В некоторых учебниках геометрии этот факт иногда приводят как иллюстрацию того обстоятельства, что две плоскости пересекаются по прямой, но такое объяснение, очевидно, неверно, ибо части сложенного листа принадлежат параллельным, а не пересекающимся плоскостям. Правильное объяснение этого факта дал Л. Р. Чейз^*. Вот как он рассуждал.

Пусть р и р' - две точки на листе бумаги, совпадающие при перегибании листа. Любая точка а, лежащая на линии сгиба, равноудалена от р и p', так как прямые ар и ар' при перегибании листа совпадают. Следовательно, линия сгиба, будучи геометрическим местом точек а, равноудаленных от р и p', перпендикулярна отрезку рр' и делит его пополам.

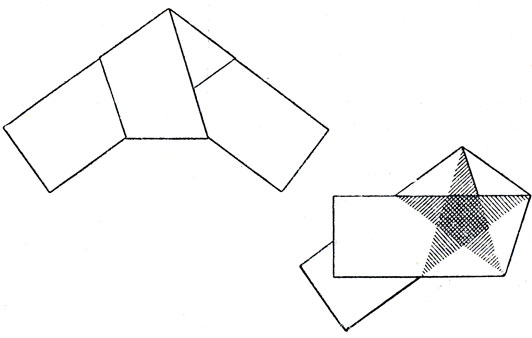
Рис. 155. Как сложить правильный пятиугольник из полоски бумаги. Слева - полоска бумаги, завязанная узлом. Если полоску согнуть еще раз так, как показано на рисунке справа, и посмотреть на свет, то будет видна 'пентаграмма'

Складывание правильных многоугольников, хотя оно и не входит в классическое оригами, может служить увлекательным упражнением для работы в классе. Равносторонний треугольник, квадрат, правильный шестиугольник и восьмиугольник сложить легко, но при складывании правильного пятиугольника могут встретиться кое-какие затруднения. Проще всего сложить правильный пятиугольник можно так: завязать полоску бумаги узлом и затем разгладить его (как это показано на рис. 155 слева). Из сложенной таким образом полоски может выйти неплохая шляпа. Если один из концов полоски перегнуть еще раз и посмотреть сквозь узел на яркий свет, то мы увидим знаменитую пентаграмму (на рис. 155 справа). В средние века пентаграмме приписывали волшебные свойства.

Перегибая лист бумаги, можно также построить различные семейства касательных, огибающими которых служат алгебраические кривые не слишком высокого порядка. Особенно легко построить параболу. Отступив от края листа, поставим на нем точку. Перегибая лист (нам понадобится сделать около 20 перегибаний), будем следить за тем, чтобы каждый раз край листа проходил через поставленную нами точку. На рис. 156 хорошо видна возникающая при этом полная иллюзия начерченной параболы. Отмеченная точка служит фокусом параболы, край листа - ее директрисой, а линия сгиба - касательной к параболе. Нетрудно видеть, что по самому построению любая точка кривой равноудалена от фокуса и директрисы. Именно это свойство и определяет параболу.

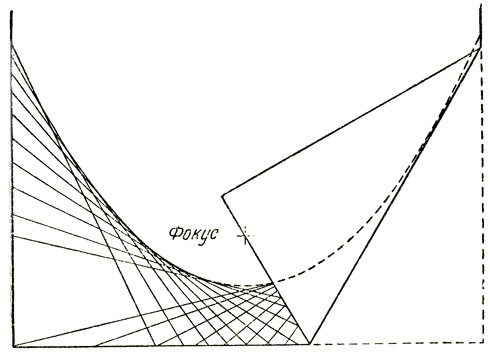
Рис. 156. Если лист бумаги согнуть так, чтобы его нижний край прошел через фокус, то линия сгиба будет касательной к параболе

Интересная задача из области элементарного анализа возникает в связи с нашим способом построения параболы. Возьмем лист бумаги размером 8 на 11 см. Перегнем его так, чтобы угол А коснулся левого края листа (рис. 157). Передвигая угол А вверх и вниз вдоль левого края и фиксируя в каждом положении линию сгиба, мы получаем семейство касательных к параболе с фокусом в правом нижнем углу развернутого листа. В какую точку левого края листа следует поместить угол А для того, чтобы линия сгиба, пересекающая нижний край листа, имела наименьшую длину? Чему равна минимальная длина линии сгиба? Читателям, не знакомым с дифференциальным исчислением, будет небезынтересно рассмотреть следующий более простой вариант этой же задачи. Уменьшим ширину листа до 7,68 см и перегнем его так, чтобы угол А совпал с точкой левого края, отстоящей от основания на расстоянии 5,76 см. Какова при этом длина линии сгиба?

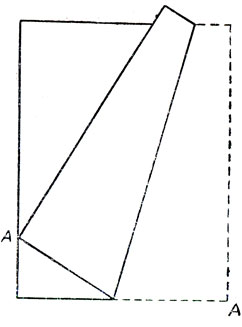
Рис. 157. Задача из анализа, возникающая при складывании бумаги

Но довольно о математической стороне искусства складывания фигур из бумаги! Сейчас я расскажу вам, как сложить из листа бумаги птицу, машущую крыльями,- одно из наиболее замечательных (с различных точек зрения) достижений оригами. Эта игрушка может служить не только образцом изящества, но и шедевром механики. Для того чтобы было легче следить за изложением, я рекомендую читателю взять квадратный лист бумаги (лучше всего для этих целей подходит плотная оберточная бумага) и самому проделать все те хитроумные манипуляции, о которых пойдет речь.

Удобнее всего работать с квадратным листом бумаги со стороной 12 см. (Некоторые искусники умудряются сделать миниатюрную птичку из сложенной в виде квадрата долларовой бумажки.) Перегните лист по двум диагоналям и переверните его на другую сторону (рис. 158, а) так, чтобы "долины" (сгибы, обращенные ребром вниз) стали "горными хребтами" (то есть сгибами, обращенными ребром вверх). На рис. 158 все "долины" показаны пунктиром, все "хребты" - сплошными линиями.

Перегните лист пополам, расправьте его и снова перегните пополам, но уже в перпендикулярном направлении, и снова расправьте. В результате на листе должны появиться еще две "долины" (рис. 158, б).

Перегнем теперь лист так, чтобы две стороны квадрата, сходящиеся в одной вершине, встретились на диагонали (рис. 158, в), расправим лист и проделаем аналогичные операции в трех остальных вершинах квадрата. В результате наш лист покроется сетью сгибов (рис. 158, г). (Заметим, что последние из сделанных сгибов образуют в средней части квадрата правильный восьмиугольник.)

Следующий этап очень трудно описать словами, но, разобравшись в существе дела, легко выполнить. Обратим внимание на четыре коротких сгиба - "долины", указанные на рис. 158, г стрелками. В этих местах перегнем лист в противоположную сторону так, чтобы эти "долины" превратились в "горные хребты". Середины сторон квадрата (на рис. 158, г они обозначены буквами А, В, С и D) сдвинем внутрь. Результат показан на рис. 158, б. Углы квадрата (обозначенные буквами I, K, L и М) приподнимутся, и все сооружение примет вид, показанный на рис. 158, е.

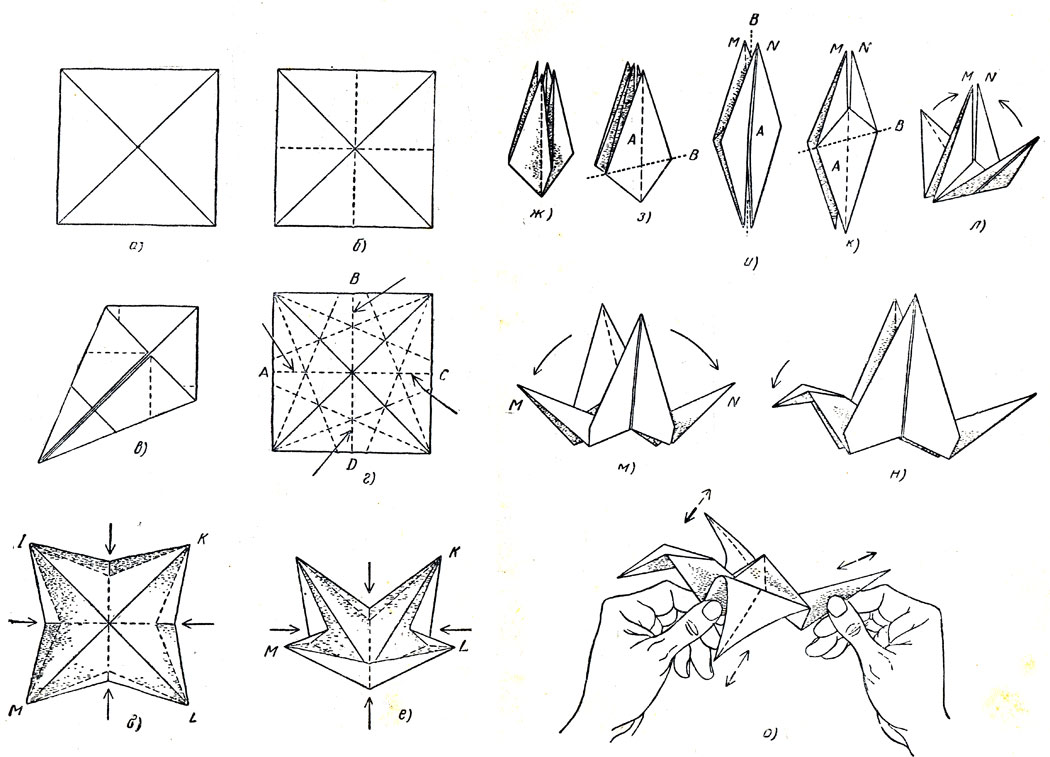
Рис. 158. Как сложить японскую птичку, машущую крыльями

Если все сгибы хорошо "отутюжены", а центр квадрата опущен до отказа вниз, то углы I, K, L и М нетрудно свести вместе (рис. 158, ж) и хорошенько разгладить заготовку, сложив выступающие углы попарно (рис. 158, з).

Отогнем выступ А (рис. 158, з) вдоль прямой В, после этого перевернем будущую фигурку на другую сторону и повторим аналогичную операцию со вторым выступом. Получившаяся фигура показана на рис. 158, а.

Перегнем клапан А (рис. 158, и) вдоль вертикальной оси В, перевернем нашу заготовку на другую сторону и повторим операцию. Результат показан на рис. 158, к.

Нижний угол А (рис. 158, к) отогнем вверх вдоль пунктирной прямой В, после чего перевернем все сооружение па другую сторону, отогнем вверх второй такой же клапан. Получившийся равнобедренный треугольник повернем так, чтобы его вершина была обращена вверх (рис. 158, л). Дальнейшие операции удобнее проделывать, держа модель на весу.

Потянув за верхушку (рис. 158, м), отогнем внутренний клапан М под некоторым углом влево и разгладим линию сгиба у основания М. Клапан N отогнем вправо. Конец клапана М вогнем внутрь и разгладим так, чтобы он стал похож на птичью голову (рис. 158, н).

Изогнем крылья (не делая новых сгибов) дугой. Если взять бумажную птичку за грудку и осторожно потянуть за хвост, она изящно взмахнет крыльями (рис. 158, о)

Птица - не единственная "действующая модель" живого существа в оригами: искусные мастера умеют складывать из бумаги разевающих рот рыбок, лягушек, которые прыгают, если их тронуть за спинку, и т. д. Переводчик Унамуно рассказывает, что великий испанский поэт любил делать "живых" зверушек и птиц, сидя за чашечкой кофе в одном из небольших ресторанов Саламанки. Нужно ли удивляться, что уличные мальчишки буквально приклеивались носами к витринам, с восхищением следя за волшебным зрелищем!

С каждым годом растет литература по оригами. Появляются в продаже комплекты, позволяющие самостоятельно складывать различные конструкции оригами. Британская энциклопедия в следующем издании решила посвятить оригами специальную статью. Воспитатели детских садов и учителя начальных школ уже начали открывать для себя этот вид искусства, но большинство из них все еще относится к нему с сильным предубеждением. В сознании этой части учителей оригами ассоциируется с широко распространенным в начале века, но пустым увлечением - вырезанием и склеиванием необычайно сложных узоров из цветной бумаги. (В педагогическую практику его ввел основатель детских садов Ф. Фребель; в США "дурное влияние" этого повального увлечения сказалось на деятельности многих учителей.)

Описание тех зверушек, которые складывал за чашкой кофе Унамуно, можно найти в английском переводе его "Очерков и монологов"^*. Ортега-и-Гассет в книге о своем друге Унамуно рассказывает, как однажды философ сложил из бумаги несколько фигурок для маленького мальчика, который спросил его, разговаривают ли между собой птички. Этот вопрос вдохновил Унамуно на создание одной из наиболее известных его поэм. У Унамуно есть юмористический очерк о складывании из бумаги и даже фундаментальная статья на эту тему.

Крупнейшим из ныне живущих художников оригами считается Акира Иошидзава из Токио. Им написано несколько книг о любимом искусстве и множество статей.

Нашу задачу о сложенном листе бумаги лучше всего решать как задачу на отыскание экстремума из анализа. Если x - расстояние от угла А (который мы накладываем на левый край листа) до точки пересечения линии сгиба с нижним краем листа, то длина остальной части нижнего края равна 8 - x. Расстояние от левого нижнего угла листа до точки, в которую попадает при сгибании листа угол А, будет равно 4√(x-4), а расстояние от угла А до точки пересечения линии сгиба с правым краем листа равно √x³/√(x-4). Приравняв производную последней функции нулю, мы найдем значение x = 6. Следовательно, угол А касается левого края в точке, отстоящей от основания на 4√2 см, а длина сгиба составляет 6√3, или немногим больше 10,392 см.

Интересная особенность этой задачи заключается в том, что минимальная длина сгиба, пересекающего нижний край листа, не зависит от ширины листа и получается при x, равном ³/₄ ширины. Три четверти ширины, умноженные на √3, дают длину сгиба. Если требуется минимизировать площадь той части листа, которая при сгибании оказывается сверху, то x всегда должен составлять ²/₃ ширины.

Длина сгиба в более простом варианте задачи (когда ширина листка бумаги была сужена до 7,68 см, а угол А помещен в точку левого края, находящуюся на расстоянии 5,76 см от основания листа) составляет ровно 10 см.