Глава 27. Магические квадраты

Представим себе квадрат, разделенный на клетки (число клеток по вертикали и горизонтали одинаково). В каждую из клеток впишем последовательные числа натурального ряда, начиная с 1, так, чтобы суммы чисел в каждой строке, каждом столбце и на главных диагоналях были одинаковы. То, что при этом получится, и будет традиционным магическим квадратом. Некоторое представление о том, каких фантастических размеров достигали сочинения о магических квадратах (предмете, не имеющем сколько-нибудь принципиального значения), можно получить из того факта, что французский трактат на эту тему, выпущенный в 1838 году, когда о магических квадратах было известно намного меньше, чем теперь, вышел в трех объемистых томах. С давних времен и поныне исследование магических квадратов процветало как своеобразный культ, часто не без мистического тумана. Среди лиц, занимавшихся изучением магических квадратов, были и известные математики, такие, как Артур Кэли и Освальд Веблен, и такие любители, как, например, Бенджамин Франклин.

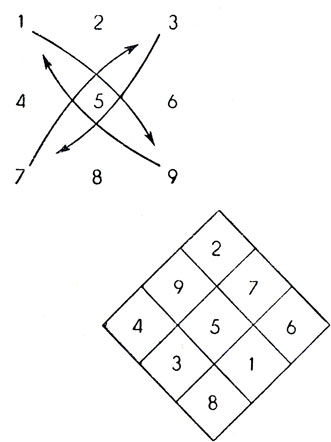
Рис. 141. Как построить талисман ло-шу

"Порядком" магического квадрата называется число клеток, примыкающих к его стороне (безразлично, к какой именно). Магических квадратов порядка 2 не существует, а порядка 3 существует только один (если не считать магических квадратов, получающихся из него при поворотах и отражениях). Запомнить единственный магический квадрат третьего порядка нетрудно. Сначала впишем во все клетки квадрата цифры в том порядке, как показано на рис. 141 слева, затем поменяем местами цифры, стоящие на противоположных концах главных диагоналей (эта операция на рисунке показана стрелками). В результате мы получим магический квадрат (рис. 141 справа), постоянная которого (то есть сумма чисел, стоящих в любой строке, в любом столбце и на каждой из главных диагоналей) равна 15. (Постоянная всегда равна полусумме n³ и n, где n - порядок магического квадрата.) В Китае, где этот магический квадрат называют ло-шу, он издавна считается талисманом. И по сей день его можно увидеть на амулетах, которые носят в Восточной Азии и в Индии, и на многих больших пассажирских судах, где он украшает крышки столиков для карточных игр.

Как только мы переходим к порядку 4, сложность магических квадратов резко возрастает. Если и на этот раз не считать различными квадраты, которые можно перевести друг в друга поворотами и отражениями, то различных магических квадратов будет ровно 880 типов, причем многие из них будут даже "более магическими", чем это требуется по определению магического квадрата. Одну из интересных разновидностей квадратов, известных под названием симметричных, можно увидеть на знаменитой гравюре Альбрехта Дюрера "Меланхолия" (рис. 142).

Рис. 142. Альбрехт Дюрер. 'Меланхолия'. В верхнем углу справа - магический квадрат

Дюрер никогда не объяснял богатую символику своего шедевра, но многие авторитеты сходятся во мнении, что гравюра изображает мрачное настроение мыслителя, не способного решиться на действие. В эпоху Возрождения меланхолический темперамент считался свойственным творческому гению, он был уделом ученых мужей, "чья бледность - печать глубоких мыслей". (Представление о том, что блестящий интеллект неспособен, подобно Гамлету, принять решение, бытует и поныне. Публичная критика, которой Гарри Трумэн во время предвыборной кампании подверг Эдлая Стивенсона, была основана именно на таком предрассудке.)

На гравюре Дюрера инструменты науки и плотницкого ремесла в праздном беспорядке лежат у ног погруженной в глубокое раздумье фигуры Меланхолии. Пусты чаши весов, никто не взбирается по лестнице, спящая борзая полумертва от голода, крылатый херувим приготовился записывать, но Меланхолия безмолвствует, а время, отмеряемое песочными часами, все бежит. Деревянный шар и причудливо усеченный каменный тетраэдр символизируют математическую основу строительного искусства. Вся сцена, по-видимому, залита лунным светом. Лунная радуга, изогнувшаяся над чем-то вроде кометы, скорее всего означает надежду на то, что мрачное настроение рассеется.

Джиорджио де Сантильяна в своей книге "The Age of Adventure" усмотрел в этой картине "загадочную и удивительную паузу человеческого разума эпохи Возрождения накануне невиданного расцвета науки". Джеймс Томсон завершает свою замечательную поэму "The City of Dreadful Night", выдержанную в пессимистических тонах, описанием именно такого настроения, которое создает гравюра Дюрера, видя в нем "еще одно проявление все того же отчаяния":

Идя на бой, готовься к пораженью, 
Нет лавров у судьбы победу увенчать; 
Молчат оракулы, и ложь - те откровенья, 
Что пифии должны нам прорицать. 
У рока тайны нет... 
Кто сможет приподнять 
Завесу, мрачную и зыбкую как тень? 
Стремимся к свету мы, но только тьма за ней.
Все суета сует... 

Астрологи эпохи Возрождения связывали магические квадраты четвертого порядка с Юпитером. Такие квадраты считались действенным средством от меланхолии (поскольку покровитель меланхоликов Сатурн и Юпитер, если верить астрологам, враждовали между собой). Вот поэтому в правом верхнем углу гравюры Дюрера изображен магический квадрат именно четвертого порядка. Дюреровский квадрат симметричен, так как сумма любых двух входящих в него чисел, расположенных симметрично относительно его центра, равна 17. Это обстоятельство позволяет выделить в квадрате много групп из четырех чисел помимо строк, столбцов и главных диагоналей, сумма которых также равна постоянной квадрата, то есть 34. Таковы, например, четыре числа, расположенных в вершинах квадрата, четыре числа в центре квадрата и четыре числа в каждом из маленьких квадратов размером 2×2, расположенных в углах большого квадрата. Существует до смешного простой способ построения таких квадратов. Стоит лишь взять квадрат, разделить его на 16 клеток и в каждую из них по порядку вписать числа от 1 до 16, а затем поменять местами числа, расположенные на главных диагоналях симметрично относительно центра, и симметричный магический квадрат готов. Дюрер переставил у своего квадрата два средних столбца (что не повлияло на свойства квадрата) так, что числа в двух средних клетках нижней строки стали указывать дату создания гравюры.

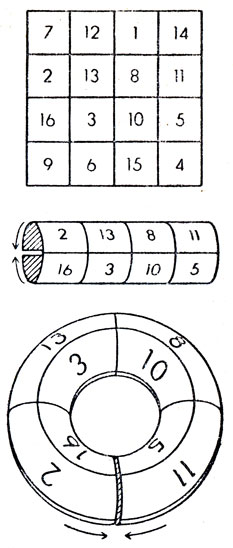
Рис. 143. 'Дьявольский' тор

Древнейший из дошедших до нас квадратов четвертого порядка был обнаружен в надписи XI или XII века, найденной в Кхаджурахо (Индия). Он показан на рис. 143 вверху. Этот магический квадрат относится к разновидности так называемых "дьявольских" квадратов (или "пандиагональных", или "насик"), еще более удивительных, чем симметричные. Помимо обычных свойств, дьявольские квадраты являются магическими по всем "ломаным диагоналям". Например, числа 2, 12, 15 и 5, а также 2, 3, 15 и 14 стоят на ломаных диагоналях, которые можно восстановить, поставив рядом два одинаковых квадрата. Дьявольский квадрат останется дьявольским, если его верхнюю строку переставить вниз или, наоборот, нижнюю строку поместить наверх, а также если вычеркнуть последний столбец справа или слева и приписать его к квадрату с противоположной стороны. Если из одинаковых дьявольских квадратов выложить мозаику (каждый квадрат должен вплотную примыкать к своим соседям), то получится нечто вроде паркета, в котором числа, стоящие в любой группе клеток 4×4, будут образовывать дьявольский квадрат. Числа в четырех клетках, следующих последовательно одна за другой, как бы они ни были расположены - по вертикали, по горизонтали или по диагонали,- в сумме всегда дают постоянную квадрата.

Вероятно, наиболее удивительный способ описания свойств дьявольских квадратов был разработан Дж. Б. Россером и Р. Дж. Уокером. Свернем квадрат в трубку, затем растянем ее и изогнем так, чтобы она превратилась в тор (рис. 143). Все строки, столбцы и диагонали дьявольского квадрата при этом превратятся в замкнутые кривые. Начав двигаться из любой клетки и сделав из нее два шага по диагонали (то есть перепрыгнув через одну клетку), мы всегда окажемся в одной и той же клетке, в каком бы направлении мы ни шли. Эту клетку называют "антиподом" той, из которой Мы начали свое путешествие. Сумма чисел в любых двух антиподах для нашего дьявольского тора равна 17. Любая замкнутая полоска из четырех клеток, расположенных вдоль меридиана, параллели или по диагонали, содержит числа, сумма которых, так же как и для любых четырех клеток, образующих на поверхности квадратную "заплатку", равна 34.

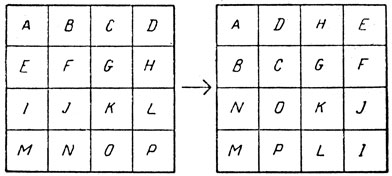
Hbc. 144. Одно из пяти преобразований, сохраняющих 'дьявольские' свойства 'дьявольского' квадрата

Дьявольский квадрат остается дьявольским, если над ним производить пять различных преобразований: 1) поворот; 2) отражение; 3) перестановку строки сверху вниз и наоборот; 4) зачеркивание столбца справа или слева и приписывание его с противоположной стороны и 5) особую перестановку клеток, схема которой показана на рис. 144. Комбинируя эти пять преобразований, можно получить 48 основных типов дьявольских квадратов (если считать, что к допустимым преобразованиям относятся повороты и отражения, то число типов возрастет до 384). Как показали Россер и Уокер, эти преобразования образуют "группу" (то есть некую абстрактную структуру, обладающую определенными свойствами), совпадающую с группой преобразований гиперкуба (четырехмерного куба) в себя.

Связь между дьявольскими квадратами и гиперкубами нетрудно усмотреть, если 16 клеток квадрата сопоставить с 16 вершинами гиперкуба. Соответствие между клетками и вершинами можно показать на хорошо знакомой двумерной проекции гиперкуба (рис. 145). Сумма чисел, стоящих в четырех вершинах каждой из 24 квадратных граней гиперкуба, равна 34. Пары антиподов, дающих в сумме 17, расположены в противоположных концах диагоналей гиперкуба.

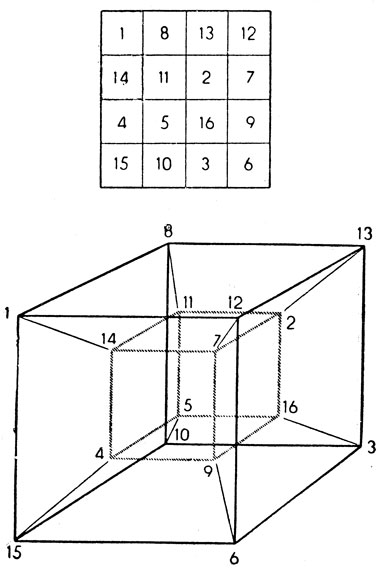
Рис. 145. 'Дьявольский' гиперкуб и один из его 384 'дьявольских' квадратов

Поворачивая гиперкуб и производя отражения, его можно перевести в 384 различных положения, каждое из которых отображается на плоскость как один из 384 дьявольских квадратов.

Клод Ф. Брэгдон, известный американский архитектор, скончавшийся в 1946 году, обнаружил, что, соединив одну за другой клетки магических квадратов ломаной, мы в большинстве случаев получим изящный узор. Подобные узоры можно получать, соединяя клетки только с четными или только с нечетными числами. Полученные таким способом "магические линии" Брэгдон использовал как образцы рисунков для тканей, книжных обложек, архитектурных украшений и декоративных заставок. Последние он сделал к каждой главе своей автобиографии. Придуманный им узор для вентиляционной решетки в потолке Торговой палаты в Рочестере (штат Нью-Йорк), где он жил, построен из магической ломаной талисмана ло-шу. Типичный пример магической ломаной показан на рис. 146, где узор вычерчен прямо на квадрате Дюрера.

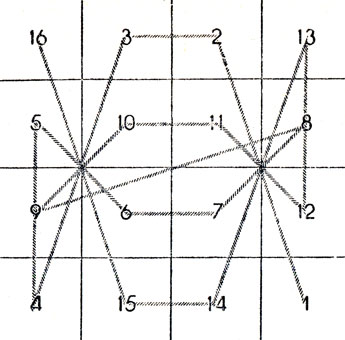
Рис. 146. 'Магическая ломаная' для квадрата Дюрера

Сколько существует различных магических квадратов данного порядка, мы не знаем. Ответ на этот вопрос относится к числу наиболее трудных задач занимательной математики. В настоящее время не известно даже число квадратов пятого порядка, хотя по некоторым оценкам оно превышает 13 миллионов. Россер и Уокер сумели установить, что число дьявольских квадратов пятого порядка равно 28 800 (квадраты, получающиеся друг из друга при поворотах и отражениях, они считали различными). Дьявольские квадраты возможны во всех порядках n, больших 4, за исключением четных я, не делящихся на 4. Например, дьявольских квадратов шестого порядка не существует. Дьявольские кубы и гиперкубы также существуют, но (как показали Россер и Уокер в своих неопубликованных работах) не бывает кубов порядка 3, 5, 7, 8k + 4 и 8k + 6, где k - любое натуральное число. Дьявольские кубы всех остальных порядков возможны^*.

^* (Интересно, что теория магических квадратов третьего и более высоких порядков находит применение в современной квантовой механике. В теории квантования моментов количества движения используется так называемая таблица Редже, которая представляет собой магический квадрат 3×3, составленный из произвольных целых чисел (не обязательно целых). Такая таблица содержит 5 не зависимых целых чисел соответственно тому, что в квадрате 3×3 есть 9 элементов, на которые наложено 5 условий равенства сумм элементов всех строк и столбцов некоторому целому числу J. Таблица Редже Имеет вид:

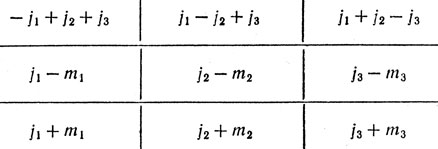
На 6 положительных чисел j и m наложены условие j₁+j₂+j₃ = J; m₁ + m₂ + m₃ = 0 и условие положительности всех 3 чисел, стоящих в первой строке. Эти условия геометрически означают, что из трех отрезков длиной j₁, j₂, j₃ можно составить треугольник, поэтому его называют "условием треугольника". Подставив в таблицу любые положительные значения j и m, удовлетворяющие написанным условиям, мы получим магический квадрат с суммой j. Естественно, этот способ легко обобщить на магические квадраты с дробными и отрицательными элементами.

Если в дополнение к приведенным условиям положить и

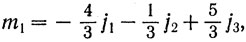
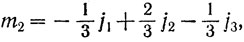
то у магического квадрата и сумма членов, стоящих на каждой диагонали, будет равна J.)