Глава 26. Занимательная логика

Слова Шерлока Холмса: "Сколько раз я говорил вам, отбросьте все невозможное, тогда то, что останется, и будет ответом, каким бы невероятным он ни казался", могли бы послужить эпиграфом к этой главе.

Если для решения головоломки требуется лишь умение логически мыслить и совсем не нужно производить арифметические выкладки, то такую головоломку обычно называют логической задачей. Логические задачи, разумеется, относятся к числу математических, поскольку логику можно рассматривать как очень общую, фундаментальную математику. Все же логические головоломки удобно выделить и изучать отдельно от их более многочисленных арифметических сестер. В этой главе мы рассмотрим в общих чертах три широко распространенных типа логических задач и постараемся выяснить, как следует подходить к их решению.

Чаще всего встречается тип задачи, который любители головоломок иногда называют "задачей о Смите - Джонсе-Робинсоне" (по аналогии со старой головоломкой, придуманной Г. Дьюдени). Она состоит из серии посылок, обычно сообщающих те или иные сведения о действующих лицах; на основании этих посылок требуется сделать определенные выводы. Вот, например, как выглядит последняя американская версия задачи Дьюдени:

1. Смит, Джонс и Робинсон работают в одной поездной бригаде машинистом, кондуктором и кочегаром. Профессии их названы не обязательно в том же порядке, что и фамилии. В поезде, который обслуживает бригада, едут трое пассажиров с теми же фамилиями. В дальнейшем каждого пассажира мы будем почтительно называть "мистер" (м-р).
2. М-р Робинсон живет в Лос-Анджелесе.
3. Кондуктор живет в Омахе.
4. М-р Джонс давно позабыл всю алгебру, которой его учили в колледже.
5. Пассажир - однофамилец кондуктора живет в Чикаго.
6. Кондуктор и один из пассажиров, известный специалист по математической физике, ходят в одну церковь.
7. Смит всегда выигрывает у кочегара, когда им случается встречаться за партией в бильярд.

Как фамилия машиниста?

Данные задачи можно было бы перевести на язык математической логики, воспользовавшись ее стандартными обозначениями, и искать решение с помощью соответствующих методов, однако такой подход был бы слишком громоздким. С другой стороны, без сокращенных обозначений того или иного рода трудно понять логическую структуру задачи. Удобнее всего воспользоваться таблицей, в пустые клетки которой мы будем вписывать всевозможные комбинации элементов рассматриваемых множеств. В нашем случае таких множеств два, поэтому нам понадобятся две таблицы (рис. 139).

Рис. 139. Две таблицы к задаче о Смите, Джонсе и Робинсоне

В каждую клетку впишем 1, если соответствующая комбинация допустима, или 0, если комбинация противоречит условиям задачи. Посмотрим, как это делается. Условие 7, очевидно, исключает возможность того, что Смит кочегар, поэтому в клетку, стоящую в правом верхнем углу левой таблицы, мы вписываем 0. Условие 2 сообщает нам, что мистер Робинсон живет в Лос-Анджелесе, поэтому в левый нижний угол таблицы мы вписываем 1, а во все остальные клетки нижней строки и левого столбца - 0, чтобы показать, что м-р Робинсон не живет в Омахе или в Чикаго, а м-р Смит и м-р Джонс не живут в Лос-Анджелесе.

Теперь нам придется немного подумать. Из условий 3 и 6 известно, что специалист по математической физике живет в Омахе, но мы не знаем его фамилии. Он не может быть ни м-ром Робинсоном, ни м-ром Джонсом (ведь тот забыл даже элементарную алгебру). Следовательно, им должен быть м-р Смит. Это обстоятельство мы отметим, поставив 1 в среднюю клетку верхней строки правой таблицы и 0 - в остальные клетки той же строки и пустые клетки среднего столбца. Третью единицу можно вписать теперь только в одну клетку: это доказывает, что м-р Джонс живет в Чикаго. Из условия 5 мы узнаем, что кондуктор тоже носит фамилию Джонс, и вписываем в центральную клетку левой таблицы и 0 - во все остальные клетки средней строки и среднего столбца. После этого наши таблицы приобретают вид, показанный на рис. 140.

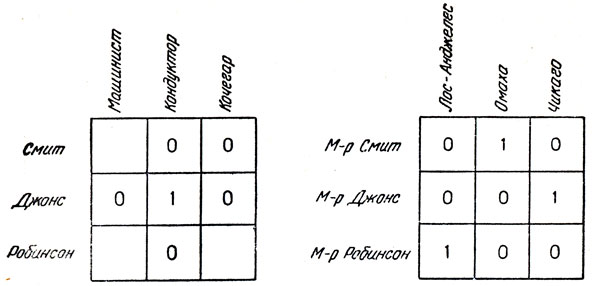
Рис. 140. Таблицы, изображенные на рис. 139, после предварительного заполнения

Теперь уже нетрудно провести рассуждения, приводящие к окончательному ответу. В столбце с надписью "Кочегар" единицу можно поставить только в нижней клетке. Отсюда сразу следует, что в левом нижнем углу должен стоять 0. Пустой остается лишь клетка в левом верхнем углу таблицы, куда можно поставить только 1. Итак, фамилия машиниста Смит.

Чрезвычайно сложные и хитроумные задачи такого рода любил изобретать Льюис Кэррол. Декан математического факультета Дортмутского колледжа Джон Дж. Кемени запрограммировал одну из чудовищных (с 13 переменными и 12 условиями, из которых следует, что "ни один судья не нюхает табак") кэрроловских задач для вычислительной машины ИБМ-704. Машина справилась с решением примерно за 4 минуты, хотя выдача на печать полной "таблицы истинности" задачи (таблицы, показывающей, истинны или ложны возможные комбинации значений истинности переменных задачи) заняла бы 13 часов!

Читателям, которые хотят попытать счастья в решении более сложной задачи, чем задача о Смите - Джонсе - Робинсоне, предлагаем новую головоломку. Ее автор Р. Смулльян (математический факультет Принстонского университета).

1. В 1918 году закончилась первая мировая война. В день подписания мирного договора три супружеские пары собрались, чтобы отпраздновать это событие за праздничным столом.
2. Каждый муж доводился братом одной из жен, а каждая жена была сестрой одного из мужей, то есть среди присутствовавших можно было указать три родственные пары "брат с сестрой".
3. Элен ровно на 26 недель старше своего мужа, который родился в августе.
4. Сестра м-ра Уайта замужем за свояком брата Элен и вышла за него замуж в день своего рождения, в январе.
5. Маргарет Уайт ростом ниже Уилльяма Блэка.
6. Сестра Артура красивее, чем Беатрис.
7. Джону исполнилось 50 лет.

Как зовут миссис Браун?

Не менее распространена и другая разновидность логических задач, которые по аналогии со следующим хорошо известным примером можно назвать задачами типа "задачи о разноцветных колпаках". Троим людям (назовем их А, В и С) завязывают глаза и говорят, что каждому из них на голову надели либо красный, либо зеленый колпак. Затем глаза им развязывают и просят поднять руку, если они видят красный колпак, и выйти из комнаты, если они уверены в том, что знают, какого цвета колпак у них на голове. Все три колпака оказались красными, поэтому все трое подняли руку. Прошло несколько минут, и С, который отличается большей сообразительностью, чем А и В, вышел из комнаты. Каким образом С смог установить, какого цвета колпак на нем?^*

^* (Задача о мудрецах в зеленых колпаках сформулирована в тексте так, что она не может иметь решения. Это особенно хорошо видно, когда число мудрецов велико. Сколько времени понадобится первому мудрецу, чтобы догадаться об истинной ситуации?

Эта задача неоднократно встречалась в литературе.)

С спрашивает себя, может ли его колпак быть зеленым. Если бы это было так, то А сразу же узнал бы, что на нем красный колпак, потому что только красный колпак на его голове мог бы заставить В поднять руку. Но тогда А вышел бы из комнаты. В стал бы рассуждать точно так же и тоже вышел бы из комнаты. Поскольку ни тот, ни другой не вышли, С заключил, что его собственный колпак должен быть красным.

Эта задача допускает обобщение на случай, когда имеется любое число людей и на всех них надеты красные колпаки. Предположим, что в задаче появилось четвертое действующее лицо D, еще более проницательное, чем С. D мог бы рассуждать так: "Если бы мой колпак был зеленым, то А, B и С оказались бы точно в такой же ситуации, какая только что была описана, и через несколько минут самый догадливый из трио непременно вышел бы из комнаты. Но прошло уже пять минут, а никто из них не выходит, следовательно, мой колпак красный".

Если бы появился пятый участник, еще более сообразительный: чем D, то он смог бы прийти к заключению, что на нем красный колпак, выждав минут десять. Разумеется, наши рассуждения теряют в убедительности из-за предположений о различной степени сообразительности А, В, С ... и довольно смутных соображений относительно того, сколько времени должен выжидать наиболее догадливый человек, прежде чем он сможет с уверенностью назвать цвет своего колпака.

Некоторые другие задачи "о цветных колпаках" содержат меньшую неопределенность. Такова, например, следующая задача, также придуманная Смулльяном. Каждый из троих - А, В и С - в совершенстве владеет логикой, то есть умеет мгновенно извлекать все следствия из данного набора посылок, и знает, что остальные также обладают этой способностью.

Берем четыре красные и четыре зеленые марки, завязываем нашим "логикам" глаза и каждому из них наклеиваем на лоб по две марки. Затем снимаем с их глаз повязки и по очереди задаем А, В и С один и тот же вопрос: "Знаете ли вы, какого цвета марки у вас на лбу?" Каждый из них отвечает отрицательно. Затем мы спрашиваем еще раз у А и снова получаем отрицательный ответ. Но когда мы вторично задаем тот же вопрос В, тот отвечает утвердительно. Какого цвета марки на лбу у В?

Третью разновидность популярных логических головоломок составляют задачи о лжецах и тех, кто всегда говорит правду. В классическом варианте задачи речь идет о путешественнике, попавшем в страну, населенную двумя племенами. Члены одного племени всегда лгут, члены другого говорят только правду. Путешественник встречает двух туземцев. "Вы всегда говорите только правду?"- спрашивает он высокого туземца. Тот отвечает: "Тарабара". "Он сказал "да",- поясняет туземец поменьше ростом, знающий английский язык,- но он ужасный лжец". К какому племени принадлежит каждый из туземцев?

Систематический подход к решению заключался бы в выписывании всех четырех возможностей: ИИ, ИЛ, ЛИ, ЛЛ (И означает "истина", Л - "ложь") - и исключении тех из них, которые противоречат данным задачи. Ответ можно получить гораздо быстрее, если заметить, что высокий туземец должен ответить утвердительно независимо от того, лжет ли он или говорит правду. Поскольку туземец поменьше ростом сказал правду, он должен принадлежать к племени правдивых, а его высокий приятель - к племени лжецов.

Самую знаменитую задачу этого типа, усложненную введением вероятностных весов и не очень ясной формулировкой, можно найти довольно неожиданно в середине шестой главы книги английского астронома А. Эддингтона "New Pathways in Science^*". "Если А, В, С и D говорят правду в одном случае из трех (независимо друг от друга) и А утверждает, что В отрицает, что С говорит, будто D лжец, то какова вероятность того, что D сказал правду?"

^* (A. Eddington, New Pathways in Science, Cambridge, 1935; Michigan, 1959.)

Ответ Эддингтона, 25/71, был встречен градом протестов со стороны читателей и породил смешной и путаный спор, который так и не был разрешен окончательно. Английский астроном Г. Дингл, автор рецензии на книгу Эддингтона, опубликованной в журнале Nature (March, 1935), считал, что задача вообще не заслуживает внимания как бессмысленная и свидетельствует лишь о том, что Эддингтон недостаточно продумал основные идеи теории вероятностей. Американский физик Т. Стерн (Nature, June, 1935) возразил на это, заявив, что, по его мнению, задача отнюдь не бессмысленна, но данных для ее решения недостаточно.

В ответ Дингл заметил (Nature, September, 1935), что если встать на точку зрения Стерна, то данных для решения вполне достаточно и ответ будет равен ¹/₃. Тут в драку вступил Эддингтон, опубликовав (Mathemetical gazette, October, 1935) статью с подробным объяснением того, как он получил свой ответ. Спор завершился еще двумя статьями, появившимися в том же журнале, автор одной из них выступил в защиту Эддингтона, а в другой выдвигалась точка зрения, отличная от всех прежних.

Трудность кроется главным образом в понимании эддингтоновской формулировки. Если В, высказывая свое отрицание, говорит правду, то можем ли мы с достаточным основанием предполагать, что С сказал, что D изрек истину? Эддингтон считал, что оснований для такого предположения недостаточно. Точно так же если Л лжет, то можем ли мы быть уверенными в том, что В и С вообще что-либо сказали? К счастью, мы можем обойти все эти языковые трудности, приняв следующие допущения (Эддингтон их не делал):

1. Никто из четырех не промолчал.
2. Высказывания А, В и С (каждого из них в отдельности) либо подтверждают, либо отрицают следующее за ними высказывание.
3. Ложное утверждение совпадает со своим отрицанием, а ложное отрицание совпадает с утверждением.

Все четверо лгут независимо друг от друга с вероятностью ¹/₃, то есть в среднем любые два из трех их высказываний ложны. Если правдивое высказывание обозначить буквой И, а ложное - буквой Л, то для А, В, С и D мы получим таблицу, состоящую из восьмидесяти одной различной комбинации. Из этого числа следует исключить те комбинации, которые невозможны в силу условий задачи. Число допустимых комбинаций, оканчивающихся буквой И (то есть правдивым - истинным высказыванием D), следует разделить на общее число всех допустимых комбинаций, что и даст ответ.

Формулировку задачи о путешественнике и двух туземцах следовало бы уточнить. Путешественник понял, что слово "тара-бара" на языке туземцев означает то ли "да", то ли "нет", но не смог догадаться, что именно. Это позволило бы предупредить несколько писем, одно из которых я привожу ниже.

Сэр!

Мне очень понравилась ваша статья о логических головоломках... Желая поделиться с женой и, вероятно, потешить свое мужское самолюбие, я рассказал ей задачу о племени лжецов и правдолюбцев. Не прошло и двух минут, как она дала разумный ответ, диаметрально противоположный приведенному у вас.

Высокий туземец, по-видимому, не понял ни слова из того, что ему сказал (на английском языке) путешественник, и не мог ответить "да" или "нет" по-английски. Поэтому его "тара-бара" означает нечто вроде: "Я не понимаю" или "Добро пожаловать в Бонго-Бонго". Следовательно, маленький туземец лгал, говоря, будто его приятель ответил "да", а поскольку маленький был лжецом, то он лгал и тогда, когда назвал лжецом высокого туземца. Поэтому правдивым следует считать высокого туземца.

Так женская логика нанесла удар моему мужскому тщеславию. Не задевает ли она немножко и ваше авторское самолюбие?

Первую логическую задачу лучше всего решать с помощью трех таблиц: одной - для комбинаций имен и фамилий жен, второй - для имен и фамилий мужей и третьей - для родственных связей. Поскольку миссис Уайт зовут Маргарет (условие 5), для имен двух других жен у нас остаются только две возможности: а) Элен Блэк и Беатрис Браун или б) Элен Браун и Беатрис Блэк.

Допустим, что имеет место вторая из возможностей. Сестрой Уайта должна быть либо Элен, либо Беатрис. Но Беатрис не может быть сестрой Уайта, потому что тогда братом Элен был бы Блэк, а двумя деверями Блэка оказались бы Уайт (брат его жены) и Браун (муж его сестры); Беатрис же Блэк не состоит в браке ни с одним из них, что противоречит условию 4. Следовательно, сестрой Уайта должна быть Элен. Отсюда в свою очередь мы заключаем, что сестру Брауна зовут Беатрис, а сестру Блэка - Маргарет.

Из условия 6 следует, что мистера Уайта зовут Артур (Браун не может быть Артуром, так как подобная комбинация означала бы, что Беатрис красивее самой себя, а Блэк не может быть Артуром, поскольку из условия 5 нам известно его имя: Уильям). Итак, мистер Браун может быть только Джоном. К сожалению, из условия 7 мы видим, что Джон родился в 1868 году (за 50 лет до подписания мирного договора). Но 1868 год - високосный, поэтому Элен должна быть старше своего мужа на один день больше тех 26 недель, о которых говорится в условии 3. (Из условия 4 мы знаем, что она родилась в январе, а из условия 3 - что ее муж родился в августе. Она могла бы быть ровно на 26 недель старше своего мужа, если бы ее день рождения приходился на 31 января, а его - на 1 августа и если бы между этими датами не было 29 февраля!) Итак, вторую из возможностей, с которой мы начали, следует отбросить, что позволяет нам назвать имена жен: Маргарет Уайт, Элен Блэк и Беатрис Браун. Никакого противоречия здесь нет, поскольку мы не знаем года рождения Блэка. Из условий задачи можно заключить, что Маргарет - сестра Брауна, Беатрис - сестра Блэка, а Элен - сестра Уайта, но вопрос о том, как зовут Уайта и Брауна, остается нерешенным.

В задаче с марками у В имеются три возможности. Его марки могут быть: 1) обе красными; 2) обе зелеными; 3) одна зеленой, а другая красной. Предположим, что обе марки красные.

После того как все трое ответили по одному разу, А может рассуждать так: "Марки у меня на лбу не могут быть обе красными (потому что тогда С увидел бы четыре красные марки и сразу узнал бы, что у него на лбу две зеленые марки, а если бы у С обе марки были зелеными, то В, увидев четыре зеленые марки, понял бы, что у него на лбу две красные марки). Поэтому у меня на лбу одна зеленая и одна красная марки".

Но когда А спросили второй раз, он не знал, какого цвета его марки. Это позволило В отбросить возможность того, что обе его собственные марки красные. Рассуждая точно так же, как и А, В исключил случай, когда обе его марки зеленые. Следовательно, у него осталась единственная возможность: одна марка зеленая, другая красная.

Несколько читателей быстро заметили, что задачу можно решить очень быстро, не занимаясь анализом вопросов и ответов. Вот что написал по этому поводу один из читателей: "Условия задачи полностью симметричны относительно красных и зеленых марок. Поэтому, распределив марки между А, В и С с соблюдением всех условий задачи и заменив красные марки зелеными и, наоборот, зеленые красными, мы придем к иному распределению, для которого все условия также будут выполнены. Отсюда следует, что если решение единственно, то оно должно быть инвариантным (не должно меняться) при замене зеленых марок на красные, а красных на зеленые. Таким решением может быть только такое распределение марок, при котором у В окажется одна зеленая и одна красная марка".

Как выразился декан математического факультета Бруклинского колледжа У. Манхеймер, это изящное решение исходит из того обстоятельства, что в совершенстве владеют логикой не А, В и С (как о том сказано в условии задачи), а Рэймопд Смулльян!

В задаче Эддингтона вероятность того, что D говорит правду, равна 13/41. Все комбинации истины и лжи, которые содержат нечетное число раз ложь (или истину), следует отбросить как противоречащие условиям задачи. В результате число возможных* комбинаций понижается с 81 до 41, из них только 13 заканчиваются правдивым высказыванием D. Поскольку А, В и С говорят правду в случаях, которые отвечают точно такому же числу допустимых комбинаций, вероятность сказать правду у всех четырех одинакова.

Используя символ эквивалентности ≡, означающий, что соединенные им высказывания либо оба истинны, либо оба ложны (тогда ложное высказывание истинно, в противном случае оно ложно), и символ отрицания ∼, задачу Эддингтона на языке исчисления высказываний можно записать так:

или после некоторых упрощений так:

Таблица истинности этого выражения подтверждает уже полученный ответ.