Глава 25. Лабиринты

В одном из древнегреческих мифов рассказывается о единоборстве юного Тезея с чудовищем Минотавром, обитавшим в кносском лабиринте на Крите. Выбраться из лабиринта Тезею помог клубок ниток, подаренный ему Ариадной. Лабиринты - архитектурные сооружения со сложными коридорами, которые строились для того, чтобы приводить в трепет непосвященных,- в древнем мире отнюдь не были редкостью. Геродот описывает египетский лабиринт, в котором было 3000 комнат. Довольно простой лабиринт изображен на монетах из Кносса; более сложные узоры в виде лабиринтов встречаются в рисунках римских мостовых и на одеждах древнеримских императоров. Такими же узорами украшали стены и полы многих соборов континентальной Европы во времена средневековья.

В Англии самым знаменитым архитектурным лабиринтом была беседка Розамунды. Повторно она была построена в вудстокском парке в XII веке королем Генрихом II, который попытался спрятать в этом лабиринте возлюбленную Розамунду Прекрасную от своей супруги Элеоноры Аквитанской. Предание рассказывает, что нить Ариадны помогла Элеоноре проникнуть в центр лабиринта, где ослепленная ревностью королева заставила несчастную Розамунду принять яд. Легенда эта поразила воображение многих авторов. На ее сюжет написал оперу Эддисон, а драматическая поэма Суинберна "Розамунда" представляет собой, по-видимому, наиболее впечатляющую версию.

Любопытно, что в Англии не принят распространенный на европейском континенте обычай украшать полы соборов мозаичными лабиринтами. Вместо этого англичане часто выкладывали лабиринты из дерна рядом с церковью. Прохождение такого лабиринта как бы являлось частью религиозного ритуала. Эти "причудливые лабиринты в пышной зелени", как назвал их Шекспир, были широко распространены в Англии вплоть до XVIII века. Садовые лабиринты из высоких кустарников, предназначенные исключительно для развлечений, вошли в моду в эпоху позднего Возрождения. В Англии самый известный лабиринт из живых изгородей, через который и по сей день пытаются отыскать путь сконфуженные туристы, был сооружен в 1690 году при дворце Вильгельма Оранского в Хэмптон-Корте. План этого лабиринта в его современном виде показан на рис. 136.

Рис. 136. План лабиринта из живых изгородей в Хэмптон-Корте

В США единственный лабиринт из кустарников, имеющий историческую ценность, был создан лишь в XIX веке членами немецкой протестантской секты, поселившимися в небольшом городке Гармония (штат Индиана). (Теперь этот городок носит название Новая Гармония. Его дал городку в 1826 году шотландский социалист утопист Роберт Оуэн, основавший там утопическое поселение.) Лабиринт в Гармонии, подобно средневековым лабиринтам, украшавшим полы соборов, символизирует змееподобные извивы греха и трудности удержания на праведном пути. Восстановлен он был в 1941 году. К сожалению, его первоначальный план не сохранился, и лабиринт был создан по совершенно новой схеме.

С математической точки зрения лабиринт представляет собой топологическую задачу. Если его план нарисовать на куске резины, то правильный путь от входа в лабиринт до цели будет топологическим инвариантом, то есть останется правильным, как бы ни сжимали и ни растягивали резину. Лабиринт, нарисованный на бумаге, можно решить очень быстро: достаточно заштриховать все тупики, тогда останутся только прямые пути к цели. Совсем иное дело, если вам, подобно королеве Элеоноре, нужно пробраться в лабиринт, планом которого вы не располагаете. Если у лабиринта имеется только один вход, а задача заключается в том, чтобы найти дорогу к единственному выходу, то ее всегда можно решить. Для этого достаточно, идя по лабиринту, все время одной рукой касаться стенки. Таким образом вы всегда найдете выход из лабиринта, хотя ваш путь вряд ли будет кратчайшим. Тот же метод пригоден и в более традиционном случае, когда цель находится внутри лабиринта, если в нем нет путей, по которым вы можете кружить вокруг цели и возвращаться в исходную точку. Если же в лабиринте имеются замкнутые маршруты вокруг цели, то, касаясь все время стены, вы просто обойдете вокруг цели по наибольшему замкнутому маршруту и снова выйдете из лабиринта. Попасть же внутрь "островка", вокруг которого проходит замкнутый маршрут, вы не сможете.

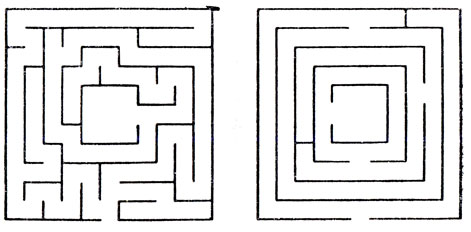
Рис. 137. Односвязный (слева) и многосвязный (справа) лабиринты

Лабиринты, не содержащие замкнутых маршрутов (например, лабиринт, изображенный на рис. 137 слева), топологи называют "односвязными". Односвязный лабиринт означает то же самое, что и лабиринт без отдельно стоящих стенок. Лабиринты с отдельно стоящими стенками заведомо содержат замкнутые маршруты под названием "многосвязиых" лабиринтов (таков, например, лабиринт на рис. 137 справа). В односвязном лабиринте, касаясь рукой стенки, вы пройдете по одному разу туда и обратно по всем закоулкам. Поэтому можно с уверенностью сказать, что где-то по дороге вы дойдете до цели. Лабиринт в Хэмптон-Корте многосвязный, но две его замкнутые петли не окружают цели. Поэтому, войдя в него и держась за стенку, вы сможете добраться до цели и выбраться наружу, ни разу не побывав при этом в какой-то из двух петель.

Существует ли способ (или, говоря языком математики, алгоритм), позволяющий находить верный путь в любых лабиринтах, в том числе и в многосвязных с замкнутыми петлями вокруг цели? Оказывается, существует. Лучше всего такой алгоритм сформулировал Э. Люка^* (правда, честь изобретения алгоритма он приписывает М. Тремо). Суть алгоритма заключается в следующем. Пробираясь по лабиринту, отметим свой путь, проводя линию у стенки, например справа. Дойдя до разветвления, мы можем выбрать любой из путей. Если, идя по новому пути, мы вернемся к перекрестку, на котором уже побывали, или попадем в тупик, то следует повернуться и идти в обратном направлении по тому же пути, по которому мы только что пришли. Если, идя по старому пути (то есть по пути, помеченному линией слева), мы вернемся к перекрестку, где мы уже были раньше, то, пройдя его, следует выбрать новый путь (если таковой имеется). В противном случае выберем старый путь. Никогда не следует идти по пути, уже пройденному дважды (с двумя отметками).

^* (E. Lucas, Recreations mathematiques, I, 1882.)

На рис. 137 справа показан многосвязный лабиринт, в котором центр окружен двумя замкнутыми петлями. Воспользовавшись алгоритмом Тремо и отмечая пройденный путь красным карандашом, читатель обнаружит, что ему действительно удастся побывать в центре и вернуться к входу после того, как он дважды (по одному разу туда и обратно) побывает во всех закоулках лабиринта. Еще лучше, если, дойдя до цели, вы не будете отмечать карандашом свой дальнейший путь: следуя только по тем дорожкам, которые отмечены одной линией, вы автоматически проложите наиболее короткий путь от входа в лабиринт до цели.

Для читателей, которые захотят испробовать предлагаемый метод на более сложном лабиринте, на рис. 138 показан план многосвязного лабиринта, построенного в своем саду английским математиком У. У. Роузом Боллом. Цель указана точкой внутри лабиринта.

Рис. 138. Лабиринт в саду У. У. Роуза Болла

В наше время взрослые люди уже не занимаются такими головоломками, однако существуют две области науки, в которых интерес к лабиринтам остается неизменно высоким: это психология и конструирование вычислительных машин. В самом деле, психологи уже в течение нескольких десятилетий используют лабиринты при изучении обученного поведения людей и животных. Даже простейшего дождевого червя можно научить пробираться по лабиринту, в котором дорожка в одном месте раздваивается. Муравьи способны после обучения преодолеть лабиринт с 10 разветвлениями. Конструкторы вычислительных машин рассматривают роботов, умеющих находить дорогу в лабиринтах, как составную часть многообещающей программы создания самообучающихся машин, то есть машин, способных, подобно животным, извлекать ценные для себя сведения из опыта.

Одним из первых устройств столь необычного типа был "Тезей" - мышь-робот, изобретенная Клодом Э. Шенноном, сотрудником Массачусетского технологического института, которая умела "самостоятельно" находить дорогу в лабиринте. Используя один из вариантов алгоритма Тремо, "мышь" сначала систематически обследует незнакомый лабиринт. Дойдя до разветвления и встав перед необходимостью выбора дальнейшего пути, мышь не действует наугад, как поступил бы человек, а, двигаясь в одну определенную сторону, всегда избирает ближайший коридор. "Нарушить работу машины, содержащей случайный элемент, весьма трудно,- объяснял Шеннон.- Ведь если вы не можете предсказать заранее, что она вообще должна делать, то вам трудно определить, делает ли она что-то не так".

После того как мышь нашла дорогу к цели, запоминающие устройства позволяют ей второй раз пройти через лабиринт уже без ошибок. На языке алгоритма Тремо это означает, что мышь будет избегать всех участков пути, пройденных дважды, и будет следовать лишь по тому маршруту, который был пройден ею только один раз. Мы не можем гарантировать, что мышь изберет кратчайший путь к цели. Можно лишь утверждать, что, идя к цели, мышь нигде не будет заходить в тупики. Живая ("настоящая") мышь обучается отыскивать дорогу в лабиринте гораздо медленнее, поскольку, обследуя незнакомый лабиринт, она в основном использует метод проб и ошибок (хотя в ее поведении имеются и другие элементы). Требуется многократный успех, чтобы правильный путь закрепился в ее памяти.

Позднее научились строить и других роботов, умеющих находить дорогу в лабиринте. Одного из самых "хитроумных" из них сконструировал Ярослав А. Дейч из Оксфордского университета. Если этот робот обучать на одном лабиринте, то он сможет перенести свой опыт на любой другой лабиринт, топологически эквивалентный первому, как бы мы ни изменяли длину и форму стенок. Робот Дейча умеет также находить кратчайшие пути в лабиринте и проделывать другие удивительные вещи.

Все эти устройства, безусловно, лишь первые шаги новой отрасли техники. Весьма вероятно, что будущие обучающиеся машины, обретя огромную мощь, станут выполнять самые неожиданные функции среди автоматов космического века. Лабиринты и космический век - эта комбинация снова возвращает нас к греческому мифу, уже упоминавшемуся в начале этой главы. Лабиринт Минотавра был построен для царя Миноса никем иным, как Дедалом, тем самым Дедалом, который изобрел крылья и чей сын Икар погиб, поднявшись слишком высоко в небо. "Столь хитро придуманного лабиринта еще не видели на свете ни до, ни после,- пишет Н. Хоуторн, пересказывая миф о Дедале.- Ничто не может сравниться с ним по сложности, разве что мозг такого человека, как Дедал, чей разум создал его, или сердце обыкновеннейшего из людей..."