
Глава 28. Фирма "Джеймс Хью Райли, аттракционы и головоломки"
Среди крупнейших американских компаний, занимающихся устройством различных развлечений, забав и зрелищ, несомненно, следует назвать фирму "Джеймс Хью Райли, аттракционы и головоломки", хотя в действительности ее... не существует.
Услышав, что на окраине города вновь открылась ярмарка с аттракционами, каруселью и т. п., я решил подъехать туда, чтобы повидаться со своим давним другом Джимом Райли. Мы познакомились с ним лет 20 назад еще в бытность студентами Чикагского университета. В то время Райли был уже на старшем курсе математического факультета, как вдруг, совершенно неожиданно для всех, он вступил в странствующую труппу, чтобы стать конферансье в танцевальном ревю. В этом амплуа, как говорят актеры, он выступал и в последующие годы. В труппе его называли Профессором. Каким-то образом ему удалось сохранить в себе живой интерес к математике, и когда бы нам ни доводилось встречаться, я всегда мог почерпнуть у него несколько оригинальных тем для раздела занимательной математики в Scientific American.
На этот раз я разыскал Профессора у входа в паноптикум, где он беседовал с контролером, проверявшим билеты. На нем была стетсоновская шляпа, и выглядел он старше и солиднее, чем при нашей последней встрече.
Регулярно читаю твой раздел в журнале,- сказал он, когда мы обменялись рукопожатиями.- Почему бы тебе не написать как-нибудь об игре "Закрой пятно"?
А что это за игра?- спросил я.
- Это один из самых старых наших аттракционов.
Он ухватил меня за руку и потащил за собой по дорожке. Вскоре мы остановились у щита, на котором был нарисован красный круг диаметром в метр. Профессор объяснил мне правила игры. Играющий должен разместить пять металлических дисков (беря каждый раз лишь по одному диску) так, чтобы они закрыли красное пятно. Диаметр каждого диска составлял, примерно 61 см. Положив диск, играющий не имеет права передвигать его. Игра считается проигранной, если после того, как положен последний, пятый диск, между металлическими дисками останется хотя бы малейший зазор и можно будет видеть красное пятно.
- Разумеется,- добавил Профессор,- из всех кругов, которые можно полностью закрыть дисками данного диаметра, мы выбрали круг наибольшего радиуса. Большинство людей считает, что диски следует располагать так.- И он разместил диски симметрично.
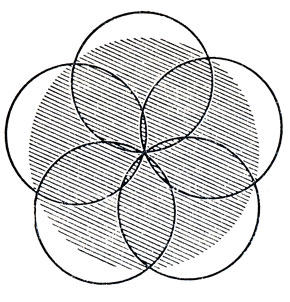
Рис. 147. Неправильное размещение дисков при игре 'Закрой пятно'
При таком расположении (рис. 147) край каждого диска проходит через центр красного круга (на нашем рисунке он заштрихован), а центры дисков образуют вершины правильного пятиугольника. Но пять маленьких кусочков у самого края красного круга остаются незакрытыми.
К сожалению,- продолжал Профессор,- такое решение неверно. Чтобы закрыть как можно большую часть круга, диски следует расположить вот так.- Он передвинул диски, и они легли так, как показано на рис. 148.
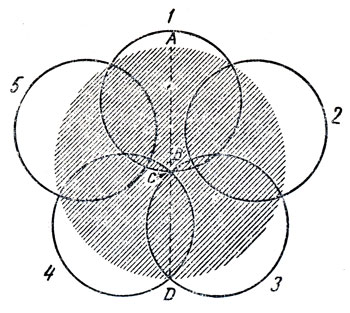
Рис. 148. Правильное размещение дисков при игре 'Закрой пятно'
Центр диска 1,- пояснил Профессор,- лежит на диаметре AD, а край диска проходит через точку С, расположенную немного ниже центра В красного круга. Диски 3 и 4 следует положить так, чтобы их края проходили через точки С и D. Диски 2 и 5 закрывают оставшуюся часть пятна.
Естественно, мне захотелось узнать, чему равно расстояние ВС. Райли не мог привести на память точные цифры, но указал мне на статью, в которой проводится подробное решение этой трудной задачи*. Если радиус пятна равен 1, то расстояние ВС чуть больше 0,285, а наименьший радиус диска будет 0,609... Если же диски расположены так, как показано на рис. 147, то для того, чтобы они полностью закрывали пятно, их радиус должен быть равен 0,6180339... (это число, обратное числу φ - золотому сечению, о котором говорилось в главе 23). Небезынтересно отметить следующую особенность задачи: разность между площадями тех частей красного пятна, которые оказываются закрытыми при первом (см. рис. 147) и втором (см. рис. 148) способах расположения дисков, очень мала и, если диаметр пятна меньше метра, едва различима.
* (Е. Н. Neville, Proceedings of the London Mathematical Society, Second Series, 14, 1915, pp. 308-326.)
- Эта игра напоминает мне,- заметил я,- одну замечательную, но до сих пор не разрешенную задачу, также связанную с минимизацией площади. Определим диаметр фигуры как длину наибольшего отрезка прямой, соединяющего две точки фигуры. Спрашивается, какова форма и площадь наименьшей плоской фигуры, которой можно накрыть любую фигуру единичного диаметра?
Профессор кивнул.
- Наименьший из правильных многоугольников, удовлетворяющих условию задачи,- это правильный шестиугольник со стороной 1/√3, но около 30 лет назад кому-то удалось улучшить это решение, отрезав у шестиугольника два угла.- Он вытащил из кармана пиджака карандаш, блокнот и тут же набросал чертеж, показанный на рис. 149. Углы шестиугольника срезаны по прямым, касательным к вписанной окружности (единичного диаметра) и перпендикулярным к прямым, проведенным из центра окружности в вершины шестиугольника.
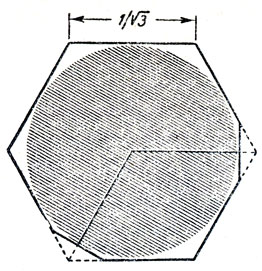
Рис. 149. Шестиугольник с обрезанными углами, которым можно накрыть любую фигуру единичного диаметра
- А это решение считается наилучшим из известных?- спросил я.
Райли отрицательно покачал головой.
- Я слышал, что несколько лет назад какой-то математик из Иллинойсского университета показал, как от усеченного шестиугольника можно отрезать еще кусочек, но подробностей не знаю.
Разговаривая, мы не спеша прогуливались по дорожке и остановились перед другим аттракционом. Он состоял из трех огромных игральных костей, которые нужно было скатывать по волнистой наклонной поверхности на расположенную внизу горизонтальную плоскость, и больших белых цифр от 1 до 6, нарисованных на специальном щите. Играющий может поставить любую сумму денег на любую из цифр. Затем он бросает кости. Если названное им число выпадает на одной из костей, он получает обратно свою ставку плюс равную ей сумму денег. Если число, на которое он поставил, выпадает на двух костях, ему возвращают его ставку плюс удвоенную сумму денег. Если же названное им число выпадает на всех трех костях, то он получает свою ставку и сверх нее утроенную сумму денег. Разумеется, если цифра, на которую он поставил, не выпадает ни на одной из костей, ставка считается проигранной.
- Разве такая игра может приносить доход?- спросил я.- Ведь вероятность выпадения задуманного числа на одной кости равна 1/6. Так как у нас имеются три кости, то вероятность выпадения числа хотя бы на одной из них равна 3/6, или 1/2. Если число выпадает более чем на одной кости, то играющий получает прибыль, превышающую его ставку. Мне кажется, что в этой игре все преимущества на стороне игрока.
Профессор довольно рассмеялся:
- Вот так простаки и попадаются. Подумай-ка получше.
Поразмыслив над этой игрой позднее, я был поражен. Может быть, некоторым читателям доставит удовольствие самостоятельно вычислить, сколько можно выиграть на каждый поставленный доллар при достаточно продолжительной игре. Когда я стал собираться домой, Райли завел меня в одну из "обираловок" (так он называл закусочные) перекусить перед дорогой. Кофе нам подали сразу же, но я решил подождать, когда принесут сандвичи.
- Если хочешь пить горячий кофе,- сказал Профессор,- лучше наливать сливки сразу. Чем горячей кофе, тем быстрее он остывает.
Я послушно налил сливки в кофе. Когда Профессору принесли его сандвич с ветчиной - два одинаковых кусочка хлеба, между которыми зажат ломтик ветчины,- он спросил:
- Тебе никогда не встречалась статья Тьюки и Стоуна "обобщенная теорема о сандвиче с ветчиной"?
- Ты имеешь в виду Джона Тыоки и Артура Стоуна - изобретателей флексатонов?
- Именно их.
Я покачал головой.
- Я не знал даже, что существует простая, не обобщенная теорема о сандвиче с ветчиной.
Райли снова вытащил свой блокнот и нарисовал сначала отрезок прямой.
- Любую одномерную фигуру всегда можно разделить на две равные по длине части с помощью одной точки. Правильно?- Я кивнул. Тогда он нарисовал две замкнутые кривые неправильной формы и прямую, которая пересекает обе нарисованные кривые (рис. 150).
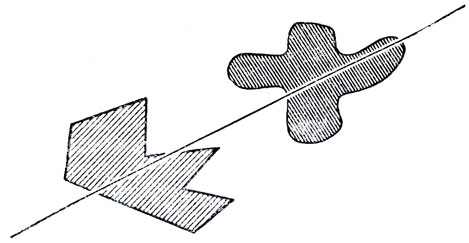
Рис. 150. К 'теореме о сандвиче с ветчиной' для размерности 2
Через любые две плоские кривые всегда можно провести прямую так, что она разделит каждую из фигур на две равновеликие (по площади) части. Правильно?
- Поверю тебе на слово.
- Это нетрудно доказать. Элементарное доказательство можно найти в книге Куранта и Роббинса "Что такое математика?"*. Оно основано на использовании теоремы Больцано.
* (Р. Курант, Г. Роббинс, Что такое математика? М., изд-во "Просвещение", 1967.)
- Я еще помню ее формулировку,- сказал я,- непрерывная функция, принимающая как положительные, так и отрицательные значения, обращается в нуль по крайней мере в одной точке.
- Верно. Теорема Больцано хотя и кажется тривиальной, тем не менее служит мощным средством для доказательства различных теорем существования. Разумеется, в интересующем нас случае теорема Больцано позволяет доказать утверждение о том, что прямая, делящая обе фигуры на две равновеликие части, существует, но ничего не говорит о том, как построить такую прямую.
- А какое отношение имеют сандвичи с ветчиной к нашей задаче?
- Это станет ясным, если перейти к трехмерному случаю. Объемы любых трех трехмерных тел, независимо от их размеров, формы и расположения в пространстве, всегда можно рассечь на две совершенно одинаковые (по объему) части одной плоскостью - так же, как ломтик ветчины в сандвиче разделяет два одинаковых кусочка хлеба. Стоун и Тыоки обобщили эту теорему на случай произвольной размерности. Они доказали, что всегда можно найти гиперплоскость, которая делит пополам четыре четырехмерных тела, как угодно расположенных в четырехмерном пространстве, или пять пятимерных тел и т. д.
Профессор выпил чашку кофе и указал на груду бубликов на прилавке.
- Если уж речь зашла о разрезании тел, то вот любопытный вопрос, который ты, может быть, как-нибудь задашь своим читателям. Каково максимальное число частей, на которые можно рассечь тор тремя плоскостями? Над этой задачей я размышляю и сам.
Закрыв глаза, я попытался представить себе, как три плоскости могут рассечь тор, но муза - покровительница аттракционов хорошенько запрятала ключ к задаче, у меня заболела голова, и наконец я сдался.
* * *
Аттракцион с тремя игральными костями известен в Соединенных Штатах под названием "Лови счастье" или "Клетка для птиц". Он широко распространен в игорных домах, где кости при бросании попадают в специальную проволочную клетку, или, как ее еще называют, "ловушку". (Иногда при бросании костей жульничают, используя электромагниты.) Один из знатокоц азартных игр отзывается об этом аттракционе так:
"Замысел игры весьма остроумен. Больше половины всех бросаний не приносит банкомету никакого выигрыша. Когда же ему случается выиграть, он тут же выплачивает в увеличенном размере выигрыши другим игрокам, и глаза проигравшего скорее с завистью устремятся на удачливого игрока, чем с подозрением - на банкомета. Выигрыши игроков сведены до минимума, и все же, когда кто-нибудь из них проигрывает, удар для него смягчается той явной щедростью, с которой банкомет выплачивает выигрыши кому-нибудь другому".
Мнения читателей по поводу того, когда лучше наливать сливки в кофе, разделились: одни были согласны с Профессором, другие считали, что сливки лучше наливать позднее, непосредственно перед тем, как пить кофе, а третьи полагали, что правы и те и другие, поскольку на самом деле выбор момента для наливания сливок роли не играет.
Я попросил Нормана Т. Гриджмена, специалиста по статистике из Канадского национального совета по исследованиям в Оттаве, разобраться в существе дела. Проведенный им анализ подтверждает мнение Профессора. Если исходить из закона остывания Ньютона (который гласит, что скорость остывания пропорциональна разности температур нагретого тела и окружающей его среды) и учесть, что объем жидкости в чашке после добавления сливок в кофе возрастает (на это обстоятельство, несмотря на его важность, часто не обращают внимания), то оказывается, что тепло лучше сохраняется в том случае, когда мы смешиваем кофе со сливками сразу, не давая ему остыть. Другие факторы - изменение интенсивности излучения из-за просветления жидкости, увеличение поверхности остывания в чашках с наклонными стенками и т. д.- оказывают столь малое влияние, что ими можно пренебречь.
Выкладки для типичного примера выглядят следующим образом. Пусть начальная температура 250 г кофе 90° С, начальная температура 50 г сливок составляет 10°С, а температура окружающей среды 20° С. Если сливки налить в кофе сразу, то температура смеси через полчаса окажется равной 48° С. Если же сливки налить через полчаса, то температура смеси будет составлять 45°С, то есть она будет на 3°С ниже.
Ответы
Бросающий кости в описанном нами аттракционе может надеяться выиграть немногим более 92 центов на каждый поставленный доллар. Три кости могут выпасть 216 равновероятными способами, в 91 случае играющий выигрывает. Поэтому вероятность выигрыша для него на каждой ставке равна 91/216. Предположим, что он бросает кости подряд 216 раз, ставя каждый раз по одному доллару, и что каждый раз кости выпадают по-разному. В 75 выигрышных для него случаях названное игроком число выпадает лишь на одной кости, следовательно, он получает 150 долларов. В 15 случаях названное число выпадает на двух костях сразу, и он получает 45 долларов. В одном случае заветное число выпадает сразу на всех трех костях, и игрок получает 4 доллара. Общая сумма, выплаченная ему, составляет 199 долларов. Чтобы получить ее, он поставил 216 долларов. Следовательно, при достаточно продолжительной игре он ожидает выиграть на каждый поставленный доллар 199/216, или 0,9212... доллара. Это означает, что владелец аттракциона на каждом поставленном игроком долларе получает прибыль в 7,8 цента, или 7,8%.
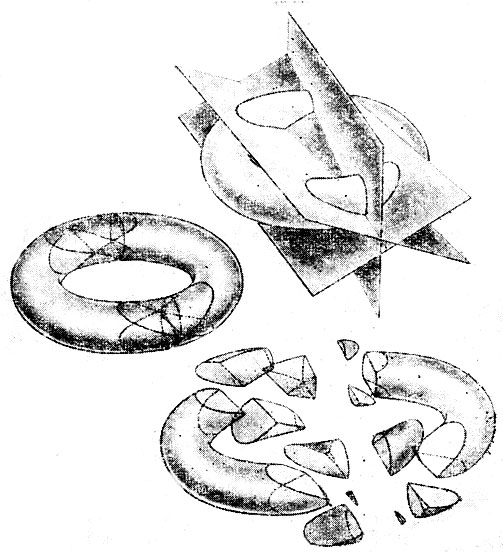
Рис. 151. Как тремя плоскостями рассечь тор на 13 частей
На рис. 151 показано, как разрезать тор на 13 частей, используя для этого три плоскости. Формула для наибольшего числа кусков, на которые можно рассечь тор n плоскостями, имеет вид
n3 + 3n2 + 8n/6
Если куски после каждого сечения плоскостью можно переставлять, то тремя плоскостями тор можно рассечь на 18 кусков.
В связи с этой задачей я получил много интересных писем. Один из читателей задал трудный вопрос: каково оптимальное отношение диаметра дырки в торе к диаметру его поперечного сечения, при котором размеры наименьшего куска, отсекаемого от тора плоскостями, будут максимальными?
Другой читатель после нескольких тщательно проведенных опытов над бубликами прислал нам следующее письмо.
Уважаемая редакция!
Некоторое размышление над задачей заставляет заключить, что максимальное число кусков равно 13. На этом вопрос можно было бы считать исчерпанным, если бы при первом же посещении булочной я не купил несколько бубликов и не обнаружил, что технические проблемы, связанные с их разрезанием, не менее увлекательны, чем математические.
Чтобы получить тринадцать кусков, из бублика необходимо вырезать узкую пирамиду, вершина которой расположена внутри бублика. Я обнаружил, что проводимые сечения удобно намечать воткнутыми в бублик зубочистками. Однако, произведя все необходимые разрезы, я так и не смог найти даже следов двух самых маленьких пирамид. (Правда, было много крошек, но они, я полагаю, не в счет.) Оказывается, что при проведении трех секущих плоскостей через бублик следует не только соблюдать все меры предосторожности при каждом разрезе, но и следить за тем, чтобы при последовательных разрезах клинообразные кусочки бублика не сдвигались относительно друг друга. Даже при соблюдении всех предосторожностей самые маленькие пирамиды чуть-чуть сдвигались, но все же не настолько, чтобы лезвие ножа могло их полностью уничтожить.
При разрезании последнего бублика я воспользовался вместо зубочисток стальными шпильками и достиг полного успеха: получилось 15 четко выраженных кусков. Все пирамиды были выше всяких похвал. Приняв чрезвычайные меры для того, чтобы предотвратить перемещения одних кусков бублика относительно других, я получил даже два лишних куска. Это произошло из-за того, что дырка в бублике не имела строго круглой формы и после проведения двух первых разрезов от бублика отделился маленький, но вполне различимый кусочек.
Может быть, очень тонкий тор типа кольца для хула-хупа разрезать было бы легче, но эта мысль появилась уже после того, как бублики были съедены, и не была исследована экспериментально.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'