Код ДНК. С. В. Голомб. Калифорнийский технологический институт, Пасадена, Калифорния

(За последние 3-4 года в изучении кода ДНК достигнуты большие успехи. Поэтому статья Голомба сейчас во многом устарела. Тем не менее мы сочли целесообразным сохранить ее при переводе сборника, поскольку ряд рассматриваемых в ней вопросов теории кодирования представляет достаточно серьезный общий интерес, независимо от биологических применений.- Прим. ред.)

1. Введение. В этой статье рассматривается проблема кодирования генетической информации при ее передаче от родителей к потомкам. Давно известно, что значительное количество информации, необходимое для построения организма, каким-то образом хранится в хромосомах каждой из его клеток. Однако существенные успехи в понимании механизма хранения этой информации достигнуты лишь в последнем десятилетии. Было показано, что генетическая информация заключена не в белках хромосом, а в других соединениях - нуклеиновых кислотах. (Более подробно биологическая сторона этого вопроса освещена в работе [1], где приведена также соответствующая библиография.)

Нуклеиновые кислоты, содержащиеся в хромосомах, относятся к типу так называемых дезоксирибонуклеиновых кислот, или сокращенно ДНК. Молекулы ДНК представляют собой длинные цепи, скрученные в двойные спирали. Каждую цепь можно условно считать перфорированной лентой, на которой пробиты отверстия четырех типов; ими и закодирована информация. Химически эти "перфорации" представляют собой четыре различные боковые группы, называемые нуклеотидами, присоединенные к остову молекулы ДНК в определенной последовательности. Таким образом, молекула ДНК представляет собой сообщение, записанное с помощью четырехбуквенного алфавита. Обычно на одной цепи ДНК размещается несколько тысяч символов, а в хромосомах содержится несколько тысяч таких цепей; все вместе это составляет полный генетический "план" организма. Эти четыре символа генетического кода обозначают буквами А, Ц, Г и Т (начальные буквы слов "аденин", "цитозин", "гуанин" и "тимин", представляющих собой названия оснований, соответствующих четырем нуклеотидам: дезоксиадениловой, дезоксицитиди-ловой, дезоксигуаниловой и тимидиловой кислотам). Все известные организмы, населяющие нашу планету, от вирусов и до самых высокоорганизованных растений и животных, используют для кодирования генетической информации четырехбуквенный алфавит нуклеиновых кислот. У некоторых организмов единственной нуклеиновой кислотой является РНК (рибонуклеиновая кислота), которая существует в виде одиночных цепей; однако в большинстве случаев генетическая информация хранится в двухцепочечной ДНК. В спаренных цепях ДНК один из элементов каждой пары представляется как бы избыточным, так как А одной цепи всегда соответствует Т другой, а Ц одной цепи всегда соответствует Г другой, и обратно. Считается, что каждая цепь ДНК может служить матрицей для синтеза другой цепи, и всякий раз, когда клетка делится, парные цепи ДНК расходятся и, присоединяя комплементарные нуклеотиды, образуют две новые парные цепи. Интересно, что такие парные цепи закручены в двойную спираль (это установили в 1953 г. Фрэнсис Крик и Джеймс Уотсон) и что спаривание цепей ДНК характерно для всех организмов, использующих ДНК; единственное исключение - один определенный бактериофаг (бактериофаги - это вирусы, убивающие бактерии), частицы которого столь малы, что вмещают только одну цепь ДНК, содержащую всего лишь несколько тысяч символов. Этот бактериофаг - простейший из организмов, известных биологам.

Суммируем сказанное: генетическая информация записана на своего рода органической ленте, называемой ДНК, с помощью четырехбуквенного алфавита: А, Ц, Г, Т. При клеточном делении "позитивная" и "негативная" копии ленты расходятся, и по позитиву образуется новый негатив, а по негативу - новый позитив; таким образом, репликация может продолжаться бесконечно.

Возникает естественный вопрос: какова природа кодируемой таким способом информации, или, иными словами, каким образом происходит считывание с "ленты" и что строится на основе прочитанного "чертежа"? Основной функцией клетки является синтез белков из блоков, называемых аминокислотами. Число различных аминокислот, используемых для этого, колеблется от 20 до 27-28, в зависимости от того, кто их подсчитывает и для какой цели. Общепринято, что при считывании происходит непосредственная интерпретация, или декодирование, и что каждая данная последовательность ну-клеотидов определяет какую-нибудь аминокислоту. В дальнейшем описании мы будем считать, что некий процесс непосредственного декодирования позволяет перейти от последовательности нуклеотидов к аминокислотам, которые образуют белковые молекулы нового организма. (В этом процессе декодирования важную роль, по-видимому, играет РНК. Общепризнано, что при считывании сообщения с ДНК оно сначала воспроизводится в матричной РНК, являющейся чем-то вроде временной памяти для всех организмов, кроме тех, которые используют только РНК и не содержат ДНК. Затем более короткие цепи растворимой РНК выполняют задачу переноса аминокислот и расположения их вдоль РНК-матрицы. В оставшейся части этой статьи такие подробности не будут приниматься во внимание, так как они не существенны для рассматриваемых ниже вопросов.) Еще одной данью ортодоксальной точке зрения будет предположение, что все населяющие нашу планету организмы используют один и тот же код. В пользу этого предположения говорит тот факт, что все известные организмы ограничиваются двадцатью с небольшим аминокислотами для синтеза белков, а если бы код эволюционировал вместе с использующими его живыми существами, то следовало бы ожидать появления на сцене и других аминокислот, столь же простых химически, как и те, которые используются сейчас. Настоящая статья посвящена попыткам четко определить проблему кодирования ДНК - белок и даже "разрешить" ее.

2. История вопроса. Первым, кто высказал, мысль, что было бы полезно подойти к вопросу о природе генетического кода с математической точки зрения, был Гамов [2]. Он предложил использовать соображения о том, какими свойствами этот код должен обладать, исходя из его функций (хотя экспериментальных данных о физической структуре нуклеотидных последовательностей почти не было). Гамов выдвинул гипотезу об одинаковой длине кодирующих блоков: он предложил считать, что для кодирования любой аминокислоты используется одно и то же число нуклеотидов. Так как сочетания нуклеотидов по два обеспечивают лишь шестнадцать возможностей, что недостаточно для кодирования двадцати с лишним аминокислот, то длина блока не может быть менее трех. Однако из трех нуклеотидов можно образовать шестьдесят четыре последовательности, так что необходимы дополнительные ограничения, чтобы теперь уже уменьшить число возможностей. Гамов предположил, что для кодирования каждой аминокислоты используется три нуклеотида, но порядок их расположения не играет роли. Так, ААВ, ABA, BAA кодируют одну и ту же аминокислоту. (Код, в котором одному объекту соответствует более чем одно кодовое слово, называется вырожденным.) Совершенно удивительным казался факт, что этот код позволял закодировать ровно двадцать различных аминокислот - в высшей степени подходящее число. Вот эти двадцать классов эквивалентных кодовых слов:

Вырожденный триплетный код Гамова является также перекрывающимся кодом, т. е. если одна аминокислота кодируется первым, вторым и третьим нуклеотидами, то следующую аминокислоту кодируют второй, третий и четвертый нуклеотиды. Такой перекрывающийся код налагает ограничения на возможные комбинации аминокислот в аминокислотной последовательности. Однако экспериментально было показано, что разнообразие фактически встречающихся комбинаций аминокислот столь велико, что гипотеза перекрывающегося триплетного кода должна быть отвергнута. Это доказал Бреннер. Основным вкладом Гамова было не то, что он разрешил проблему, а то, что он увидел и сформулировал ее.

Главной причиной, по которой Гамов предложил перекрывающийся триплетный код, была попытка избежать проблемы синхронизации, возникающей в случае неперекрывающегося кода. Так, если АТА и ЦТГ - кодовые слова двух соседних аминокислот, то при их последовательном расположении комбинация ... АТАЦТГ ... содержит, кроме триплетов АТА и ЦТГ, также триплеты ТАЦ и АЦТ, которые могут кодировать две другие аминокислоты. Если благодаря какому-либо химическому процессу эти аминокислоты образуются раньше, то смысл генетического сообщения будет утрачен.

Другой подход к проблеме синхронизации, предложенный Криком и др. [3], состоит в предположении о существовании триплетного неперекрывающегося кода, названного Криком кодом без запятой. Код называется кодом без запятой, если для любых кодовых слов (а₁а₂ ... a_k) и (b₁b₂ ... b_k), одинаковых или нет, никакое из "промежуточных" слов, появляющихся при выбрасывании запятой из записи а₁а₂ ... a_k, b₁b₂ ... b_k - а именно слова (а₂ ... a_kb₁), (a₃ ... b₁b₂), ..., (a_kb₁ ... b_k-1),- не является словом из словаря. Например, если в словаре кода без запятой есть слова MAN и DOG, то слова AND там не должно быть (чтобы исключить mANDog). Если в словаре есть слово EAT, то в нем не должно быть ни ATE ни TEA, чтобы исключить eAT Eat и eaTEAt. В словаре не должно быть также слов типа XXX, так как иначе возникла бы проблема синхронизации при расшифровке ... XXXXXX ...

Крик и др. показали, что словарь кода без запятой при четырехбуквенном алфавите и словах из трех букв включает максимум двадцать слов, и привели примеры таких словарей. В словаре

буквы a, b, c, d могут быть отождествлены с нуклеотидами А, Ц, Г, Т любым из 4! = 24 способов.

В работе [4] получены некоторые общие математические результаты относительно кодов без запятой, использующих k-буквенные слова n-буквенного алфавита. Применение этих методов к биологическим ситуациям подробно рассмотрено в [1], где описаны все возможные словари кодов без запятой, состоящие из двадцати слов при k = 3 и n = 4. Было показано, что в любом сообщении, составленном с помощью такого словаря, один и тот же символ не может подряд повторяться более чем три раза. Однако последующие эксперименты показали, что в ДНК нуклеотиды иногда повторяются четыре и даже пять раз подряд, из чего следовало, что гипотеза триплетного кода без запятой неверна - по крайней мере в той простой форме, в которой она описана в работе [3]. Это не исключает, правда, возможности, что используемый код есть код без запятой, но с длиной слова (что существенно) более трех.

Последующие разделы настоящей статьи содержат краткий обзор теории кодов без запятой, обсуждение параметров, ограничений и предположений, делаемых при рассмотрении проблемы генетического кодирования, описание "биортогональных кодов" и их отношения к генетическому коду, попытки синтеза некоторых из этих концепций в новую модель генетического кода, которая объясняет (верно или неверно) экспериментальный феномен, известный под названием генетических "горячих точек", а также возможные пути эволюции. В заключительной части приведен список основных вопросов, которые, быть может, окажутся разрешимыми с помощью подходящих экспериментов и ответы на которые будут иметь важное значение как для проблемы кодирования, так и для понимания генетического процесса в целом.

3. Современное состояние теории кодов без запятой. Хорошей иллюстрацией известного положения о том, что биологические проблемы могут приводить к интересным математическим теориям, которые в свою очередь могут находить приложения в самых разных областях, являются коды без запятой. С тех пор как Крик и др. [3] предложили эту проблему в ее биологическом контексте, она уже рассматривалась как комбинаторная проблема, представляющая математический интерес [4], а впоследствии [5] - как проблема, представляющая интерес для инженеров-специалистов по теории связи, так как она относится к общей проблеме эффективной передачи информации.

Нижеследующий краткий обзор теории* кодов без запятой основан на статье [6]. Для более полного ознакомления с основными результатами мы отсылаем читателя к работам [1, 3, 4]. В приведенном далее обсуждении использованы результаты Баумерта, Хейлса, Джуита и Селфриджа, а также авторов работы [4].

а) Введение. Набор D k-буквенных слов называется словарем кода без запятой, если для любых двух слов (a₁a₂ ... a_k) и (b₁b₂ ... b_k) из D никакие из промежуточных слов (а₂а₃ ... a_kb₁), (a₃a₄ ... a_kb₁b₂) ..., (a_kb₁ ... b_k-1) не принадлежат D. Два k-буквенных слова принадлежат одному и тому же классу эквивалентности, если одно из них получается из другого циклической перестановкой. Класс эквивалентности называется полным, если он содержит k различных элементов.

Свойство кода быть кодом без запятой нарушается, если в словаре присутствуют слова из неполных классов эквивалентности или если из одного и того же класса выбирается более одного слова. Поэтому если слова образуются из фиксированного n-буквенного алфавита, то можно определить верхнюю границу объема словаря кода без запятой, подсчитав число полных классов эквивалентности. Пусть W_k(n) обозначает наибольшее число слов, которое может содержаться в таком словаре. Тогда [4]

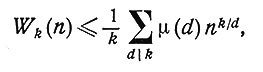
(1)

где суммирование производится по всем делителям d числа k, a μ(d) - функция Мёбиуса, определяемая равенствами

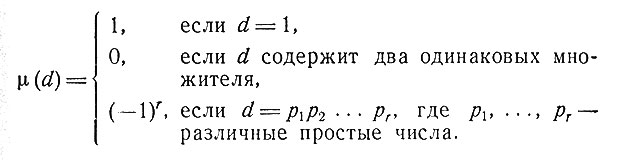
Первые (последние) n букв слова называются начальной (финальной) n-граммой (для чисел 2, 3, 4 используются соответственно названия диграмма, триграмма, тетраграмма).

В работах [4] и [1] исследуются эти коды и доказывается много их свойств. Мы остановимся в основном на результатах, полученных после опубликования работ [4] и [1].

б) Результаты для четных k. Приведенная ниже теорема 1 есть усиление теоремы 4 из [4].

Теорема 1. Если k = 2j, то при n>2^j+j верхняя граница для W_k(n), задаваемая соотношением (1), не достигается.

Теорема 2. Если при k = 2i, n≥4 объем словаря D достигает верхней границы, задаваемой соотношением (1), то каждая буква встречается в каждой позиции.

Следствие. Если k = 2i, n≥4 и объем D достигает верхней границы, то никакая начальная (k-1)-грамма не является финальной (k-1)-граммой.

Теорема 3. Если k = 4, n>2, то объем D достигает верхней границы лишь при условии, что никакая начальная триграмма не является финальной триграммой.

Теорема 4. W₄(4)<60.

Доказательство этого результата основано на следующих леммах. Пусть |D| обозначает число слов в D.

Лемма 1. Если |D| = 60 и n = k = 4, то каждая диграмма является либо начальной, либо финальной.

Лемма 2. Если |D| = 60 и n = k = 4, то каждая буква начинает (оканчивает) по крайней мере две начальные и две финальные диграммы.

Лемма 3. Если |D| = 60 и n = k = 4, то не каждая диграмма, начинающаяся (оканчивающаяся) буквой X, является одновременно начальной и финальной.

Лемма 4. Если |D| = 60 и n = k = 4, то каждая буква начинает диграмму, которая является одновременно начальной и финальной.

Лемма 5. Если |D| = 60 и n = k = 4, то никакая буква не начинает три диграммы, являющиеся одновременно начальными и финальными.

Лемма 6. Если |D| = 60 и n = k = 4, то никакая буква не начинает три диграммы, не являющиеся одновременно начальными и финальными.

Лемма 7. Если все диграммы, начинающиеся с фиксированной буквы, являются начальными (финальными), то |D|<60, n = k = 4.

Лемма 8. Если в точности три начальные и три финальные диграммы начинаются с одной и той же буквы, то |D)|<60, n = k = 4.

Теорема 5. Если n = k = 4, |D|>56, то никакая начальная триграмма не является финальной.

в) Результаты расчетов. Для n = 2, k = 8 были найдены коды, достигающие верхней границы (1). Если использовать в качестве алфавита символы 0 и 1, то такой код должен удовлетворять неравенствам

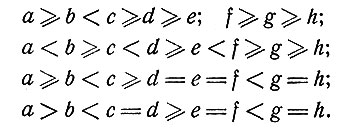
С помощью перебора было показано, что W₄(4) = 57. Так как эта процедура потребовала больших затрат времени при выполнении ее на цифровой вычислительной машине, то проверка результатов с помощью ручного счета не представляется возможной. Поэтому было бы интересно математическое доказательство этого факта. Заметим, что все словари из 57 слов, найденные при этих расчетах, пропускают классы одного и того же типа, а именно один класс типа (xyzw) и два класса типа (pgpr). Типичным кодом, достигающим верхней границы 57, является следующий:

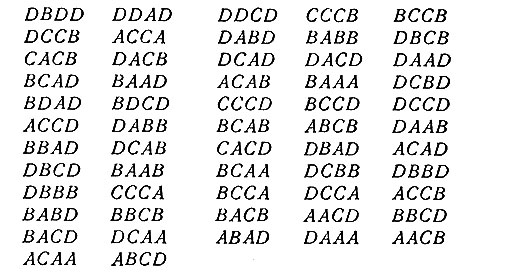
После трудоемких расчетов оказалось, что исчерпывающий перебор с целью поиска кодов, достигающих верхней границы, равной 116, для случая n = 3, k = 6 неосуществим. Однако расчеты на вычислительной машине показали, что верхняя граница 116 не достигается, если слово ААВВСС используется в качестве представителя своего класса. Таким образом, любой код, достигающий верхней границы 116, должен быть изоморфен коду, содержащему АВВССА.

г) Результаты для нечетных k. Методом, используемым при доказательстве теоремы 2 из работы [4], было показано, что I7w₁₇(n) = n¹⁷ - n, так что коды без запятой, достигающие верхней границы (1), существуют для всех нечетных k≤17 при всех значениях n.

Далее было показано, что при всех нечетных k верхняя граница (1) достигается для класса словарей, удовлетворяющих более слабому ограничению, чем свойство быть словарем кода без запятой. А именно, набор D k-буквенных слов при n-буквенном алфавите называется локально дешифруемьм, если для любых слов (a₁ a₂ ... а_k) и (b₁ b2 ... b_k) из D при любых i = 1, 2, ..., k-1 не выполняются одновременно следующие три условия:

Ясно, что каждый словарь кода без запятой является локально дешифруемым, но не обратно. Этот результат заставляет усомниться в том, что W_k(n) должно достигать верхней границы (1) при всех нечетных k, как это предсказывалось в [4].

д) Асимптотика. Был получен следующий результат, являющийся усилением теоремы 7 из [4]. Обозначим

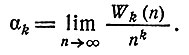
Теорема 6. Для четных k>2

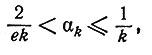
где e = 2, 71828... .

Как показано в работе [4], α₂ = ¹/₃ и W₂(n) =[n²/3], где квадратные скобки означают "целую часть".

4. Параметры, ограничения, предположения. Один из немногих твердо установленных фактов относительно генетического кода состоит в том, что сообщение написано с помощью четырехбуквенного алфавита, состоящего из символов А (аденин), Ц (цитозин), Г (гуанин) и Т (тимин). Считается, что нуклеотидные триплеты кодируют индивидуальные аминокислоты, число которых заключено между 20 и 28 (т. е. 24±16%). Недавние эксперименты показывают, что для кодирования каждой аминокислоты используется в среднем от 4 до 8 символов (нуклеотидов), т. е. "кодовое число" равно 6±33%. Эти экспериментальные данные противоречат триплетно-му коду, предложенному как Гамовым [2], так и Криком и др. [3].

Во всех работах, посвященных проблеме кодирования, предполагается однородный код, т. е. код, использующий одно и то же число нуклеотидов для кодирования каждой аминокислоты. Хотя это предположение поддерживается структурными соображениями и, кроме того, удобно для математического рассмотрения, но прямых экспериментальных подтверждений его нет. Кажущееся отсутствие ограничений на комбинации аминокислот друг с другом является сильным аргументом против перекрывающихся кодов [2], при которых, кроме того, кодовое число должно быть очень небольшим (очевидно, единица); это казалось правдоподобным в 1954 г., но сейчас считается невероятным.

Вырожденный код - это код, ставящий в соответствие одному объекту несколько кодовых слов. Вырожден ли генетический код, неизвестно. Код называется полностью дешифруемым, если при пользовании им всякая последовательность символов может быть интерпретирована как сообщение, т. е. если невозможно образовать бессмысленный, нерасшифровываемый текст. Перекрывающийся триплетный код Гамова вырожден и полностью дешифруем. Код без запятой Крика не является ни вырожденным, ни полностью дешифруемым. Ответ на вопрос, существует ли последовательность нуклеотидов, которая не может быть дешифрована как белок, экспериментально не получен.

О механизме считывания с ДНК при синтезе белков известно очень немного. Если считывание начинается с одного конца цепи ДНК и происходит последовательно вплоть до другого ее конца, то обеспечение синхронизации не представляет проблемы, особенно в случае кодовых групп одинаковой длины. Однако если считывание происходит одновременно по всей цепи ДНК, что весьма вероятно с химической точки зрения, то использование кода без запятой обязательно.

В течение последних двух лет было получено много экспериментальных данных о последовательности расположения нуклеотидов в молекулах ДНК различных организмов. Был проведен статистический анализ последовательных пар нуклеотидов, изучение распределения последовательностей пуринов (А и Г) и пиримидинов (Ц и Т), а также некоторые другие исследования. Хотя полученные данные и не привели к созданию четких представлений о генетическом коде, любое детальное объяснение явлений, связанных с кодированием генетической информации, должно согласовываться с этими экспериментальными результатами. Изучение структуры ДНК значительно затрудняется тем фактом, что молекулы ДНК существуют в виде спаренных комплементарных цепей. Например, суммарное число АА-диграмм равно суммарному числу ТТ-диграмм просто в силу комплементарное, хотя, если бы было возможно получить статистические результаты для отдельной цепи ДНК, эти числа могли бы оказаться совершенно различными.

5. Биортогональные коды.Адамаровой (n×n)-матрицей называется матрица, состоящая из +1 и -1 и обладающая тем свойством, что любые две ее строки ортогональны (т. е., по статистической терминологии, некоррелированы). Если к списку n векторов-строк присоединить эти же n векторов-строк со знаком минус, то мы получим набор из 2n векторов, или кодовых слов, обладающих тем свойством, что кросс-корреляция между двумя различными кодовыми словами равна либо О (в большинстве случаев), либо -1 (в некоторых избранных случаях).

Благодаря ортогональности достигается возможность различать кодовые слова; это один из типов избыточности, благодаря которому наиболее эффективно обеспечивается надежность при передаче информации.

Условия существования адамаровых матриц и основные сведения об их структуре содержатся в работе [7], где, в частности, показано, что для того чтобы существовала адамарова матрица порядка n>2, необходимо, чтобы n делилось на 4. Идея использования строк биортогональных матриц в качестве кодов, несущих информацию, восходит к кодам Рида - Мюллера [8], хотя эти коды определены только для n, являющихся степенями двойки.

Чтобы можно было использовать биортогональные коды для решения проблемы генетического кодирования, должны быть выполнены некоторые необходимые условия. Во-первых, алфавит должен состоять не из двух символов, а из четырех. Во-вторых, величина n должна быть выбрана так, чтобы суммарное число кодовых слов согласовывалось с требуемым числом аминокислот. В-третьих, необходимо учитывать ограничения, налагаемые проблемой синхронизации (код без запятой). Удовлетворяющие этим ограничениям коды (если таковые найдутся) должны быть использованы с целью получения их экспериментально проверяемых характеристик, включая сюда попытки математически вывести хотя бы некоторые из феноменологических свойств генетического процесса.

Возможные значения n для адамаровой (n×n)-матрицы - это 1, 2, 4, 8, 12, 16, 20, ... . Возникающие при этом биортогональные словари имеют размеры 2, 4, 8, 16, 24, 32, 40, ... . Величина 24 является идеальной с точки зрения числа аминокислот. (История, однако, показывает, что не стоит слишком радоваться всякий раз, когда удается подобрать семейство кодов так, что число кодовых слов приблизительно соответствует числу аминокислот!) Обозначив символы четырехбуквенного алфавита через +1, i, -1, -i, а символы двоичного алфавита через 1 и 0, можно установить следующее соответствие между четверичными символами и парами двоичных;

Для двух "комплексных" векторов v₁ и v₂ с компонентами из этого четырехбуквенного алфавита подходящей мерой корреляции является C(v₁, v₂) = Re(v₁*v₂), т. е. действительная часть их скалярного произведения. Такой выбор меры корреляции обеспечивает для векторов, угол между которыми равен 0°, корреляцию +1, при угле 90° - корреляцию 0, а при угле 180° - корреляцию - 1, что априори и хотелось бы иметь. Мы не будем устанавливать соответствия между алфавитом нуклеотидов (А, Г, Ц, Т) и алгебраическим четырехбуквенным алфавитом (+1, i, -1, -i), хотя здесь и могут быть высказаны различные суждения.

Рассмотрим теперь биортогональные коды. Существует много преобразований (2n×n)-матрицы, сохраняющих биортогональность. Именно, никакая перестановка столбцов не влияет на корреляцию строк. Кроме того, любое число столбцов может быть обращено (т. е. умножено на -1) без изменения корреляции. Таким образом, существует группа из 2ⁿ*n! перестановок и обращений столбцов, порождающая только такие коды, которые обладают свойством биортогональности. Для n = 12 предварительный расчет показал, что среди словарей, которые можно получить таким путем из исходного словаря, имеется 2¹¹ = 2048 различных. (Если некоторая перестановка столбцов дает тот же результат, что и перестановка строк, то полученный словарь эквивалентен исходному, так как порядок расположения кодовых слов не является существенной характеристикой словаря.) Даже если исходный биортогональный словарь не является словарем кода без запятой, не исключено, что он будет переведен в таковой с помощью описанных преобразований (перестановок и обращений). В табл. 1 приведен биортогональный словарь из 24 слов (где использованы символы 0 и 1 вместо +1 и -1); словарь, полученный из него обращением последней цифры каждого слова (0 заменен на 1, а 1 на 0), и результат преобразования двоичного алфавита в четырехбуквенный. В итоге получился словарь кода без запятой, состоящий из 24 слов, а каждое слово - из шести четверичных символов. Параметры этого словаря находятся в наилучшем соответствии с современными экспериментальными данными. Избыточность использована для достижения максимальной различимости слов, обеспечивая таким образом эффективное кодирование в смысле теории информации. В двоичной форме этот код может быть описан как код, корректирующий две ошибки и обнаруживающий три. Перефразируя это для четверичного кода, мы можем сказать, что этот последний позволяет скорректировать суммарную ошибку менее 270° и обнаружить ее, если она равна 270°. Это означает, что если суммарная ошибка не превосходит 270°, то искаженное слово имеет большую корреляцию с его исходной формой, чем с любым другим словом из словаря. Если же ошибка равна 270°, то корреляция с исходным словом по крайней мере не меньше, чем с любым другим кодовым словом. Правдоподобность предположения об участии в генетическом процессе кодов, корректирующих ошибки, обсуждается в следующем разделе, где рассматриваются биортогональные коды с биологической точки зрения.

Таблица I

6. Биортогональные коды, "горячие точки" и возможные пути эволюции. С полинуклеотидной цепью ДНК связаны два различных процесса. Один из них - синтез ДНК, осуществляющийся посредством репликации цепи. Другой - синтез белка, для которого необходимо считывание с ДНК. Ошибки, происходящие при этих двух процессах, в корне различны. Здесь мы рассмотрим следующую гипотезу.

Гипотеза. Генетический код основан на биортогональном словаре из 24 слов, состоящих из шести четверичных символов. Репликация обычно осуществляется безошибочно, если только не действуют мутагенные факторы. Если в ДНК последовательность нуклеотидов не соответствует стандартному коду какой-либо аминокислоты, то при считывании осуществляется коррекция ошибки.

Можно предложить и более явную модель. Каждый блок из шести нуклеотидов благодаря химическому сродству в конце концов присоединяет аминокислоту. Если в блоке нет ошибок, то это присоединение происходит быстро, благодаря чему свойство кодов без запятой самосинхронизироваться проявляется также и в случае редко рассеянных ошибок. После расшифровки всех безошибочных блоков будут заполняться блоки с одной ошибкой, и лишь затем - с двумя.

Вовсе не обязательно предполагать полную дешифруемость кода (отсутствие бессмысленных сочетаний в коде); это свойство легко получится само. В случае тройной ошибки будет присоединена одна из тех аминокислот, которые одинаково подходят для данного кодового слова; если же вычислить точные величины химического сродства, то возможно, что в каждом случае будет лишь одна наиболее подходящая аминокислота. В случае четырех ошибок весьма вероятно, что получившееся слово будет больше похоже на некоторое новое, чем на исходное,- произошла мутация.

Феномен генетической "горячей точки" можно описать следующим образом. Мутации в данном организме возникают на одних участках генетической ленты значительно легче, чем на других, например при воздействии химических мутагенов. Эти изменчивые участки и называются "горячими точками". Расположение "горячих точек" передается по наследству от родителей к потомкам, хотя у представителей различных "триб" одного и того же вида могут быть различные "горячие точки". Кроме того, большинство участков генетической ленты, по-видимому, не может превращаться в "горячие точки".

С помощью кодов, корректирующих ошибки, легко можно объяснить наличие "горячих точек" с разной степенью чувствительности. Если ни один из шести символов данного слова не изменен, то блок можно считать "холодным", так как в этом случае должно было бы произойти слишком много ошибок, чтобы их влияние сказалось на синтезе белка. В случае одиночной ошибки (90°) достаточно меньшего числа ошибок, так что мы имеем "теплую" точку. В случае двух одиночных ошибок (каждая по 90°) или одной двойной (180°) уже легко получить регистрируемую мутацию, и мы имеем настоящую "горячую" точку. При тройной ошибке получится "сверхгорячая" точка. Ясно, что возникновение благодаря такой "частичной" мутации горячих точек является наследственным признаком, который, однако, не обязательно проявляется у всех особей данного вида.

Однако возможны и возражения против такого описания. Во-первых, не исключена возможность того, что генетический код является просто вырожденным кодом, в котором одной и той же аминокислоте соответствует несколько различных последовательностей нуклеотидов, так что введение представления о кодах, корректирующих ошибки, ничего не дает. Во-вторых, не обнаружено механизма, который бы предотвращал появление или хотя бы проводил отбор, направленный против появления частичных мутаций, или субмутаций, воздействующих на ДНК, но не проявляющихся в синтезе белка, благодаря чему все участки должны иметь тенденцию становиться чувствительными. Кроме того, это описание никак не объясняет того факта, что некоторые участки всегда остаются "холодными" и лишь определенные участки могут стать "горячими точками".

Все затруднения легко преодолеваются, если должным образом ввести ограничения, налагаемые кодом без запятой. Удобно предположить, что если сообщение, записанное на ДНК, нарушает это ограничение, то синтез соответствующего белка не происходит и никакого результата не будет обнаружено. Таким образом, ошибки, нарушающие требования кодов без запятой, никогда не будут обнаружены на уровне синтеза белка. Поскольку очень большая часть всех ошибок нарушает эти требования, то этим можно объяснить известный из экспериментов факт, что лишь некоторые определенные участки могут стать "горячими точками". Число различных мутаций в разных "горячих точках" неодинаково, быть может, потому, что в одних участках требования кода без запятой сохраняются лишь при замене не более чем одного старого нуклеотида новым, а в других участках могут оказаться допустимыми все три ошибки. Скорость декодирования также может иметь значение для отбора, обеспечивая тенденцию к исключению субмутаций и контролируя их частоту. Поскольку не все различные представления одной и той же аминокислоты могут быть одинаково удачными (в отношении времени декодирования, возможности быть кодом без запятой и т. д.), становится затруднительным доказать, что генетический код не является обычным вырожденным кодом, а в нем есть "избранные" кодовые слова, которые даже при искажениях поддаются прочтению.

Идея о возможности субмутаций (т. е. ошибок или изменений в ДНК, не проявляющихся в синтезе белков) является сама по себе новой, и ее экспериментальное подтверждение или опровержение было бы в высшей степени желательно. Развивая это представление и требуя, чтобы субмутации удовлетворяли ограничениям, налагаемым кодами без запятой, можно получить непосредственные выводы о возможных путях эволюции. Для всякого допустимого эволюционного изменения, осуществляющегося благодаря мутации ДНК, необходимо, чтобы не только исходная и конечная формы, но и формы, возникающие на промежуточных этапах при субмутациях, были допустимыми (точнее, удовлетворяли требованиям кодов без запятой). Легко построить примеры, из которых видно, что допустимые субмутации не являются коммутативными операциями и что если происходит по одной субмутации за раз, то не всегда возможно попасть из состояния А в состояние В, не нарушив при этом требований кодов без запятой. Однако существует вероятность, не исключенная с биологической точки зрения, что две субмутации произойдут одновременно и позволят коду развиваться по новым путям.

Коды такого типа, как четверичный код, приведенный в табл. 1, не только оказались удовлетворительными по всем параметрам, но также позволили объяснить феномен генетических "горячих точек" и указать допустимые пути эволюции организма. Хотя эта кодовая система оказалась в высшей степени эффективной и, по-видимому, удовлетворяет основным ограничениям, известным в настоящее время, все же очень вероятно, что не на ней основана земная жизнь. Однако и в этом случае можно привлечь стандартный аргумент о миллионах галактик с миллиардами звезд, окруженных планетами, и считать, что по крайней мере на одной из планет жизнь основана на описанных здесь кодах и, без сомнения, является в некотором смысле более удачной, чем земная.

7. Обзор основных результатов. Основной философский вопрос, поднимаемый настоящей работой, состоит в следующем: является мутация в обычном понимании этого слова (т. е. мутация на уровне синтеза белка) делимой или неделимой? Предложенное здесь объяснение феномена "горячих точек" основано на допущении того, что при образовании ДНК возможны столь малые ошибки, что они не проявляются в синтезе белков. Это представляет собой аналогию с рецессивными мутациями, правда весьма поверхностную. Однако здесь для проявления эффекта необходимо, чтобы произошли дальнейшие ошибки.

Другой фундаментальный вопрос: существуют ли генетически бессмысленные сообщения? Прочитывается ли всякий блок хоть как-нибудь или существуют не имеющие смысла наборы символов, которые прекращают процесс декодирования? Далее, если используются коды без запятой, то, кроме проблемы интерпретации кода при отсутствии всякой информации о синхронизации, возникает вопрос: как можно воспользоваться такой информацией для выявления смысла слов, переданных с ошибками? (Заметим, что код без "бессмыслицы" почти наверняка должен быть вырожденным, т. е. нескольким кодовым словам должна соответствовать одна и та же аминокислота.)

Еще один интересный вопрос, хотя и не такой фундаментальный,- сравнение надежности репликации с надежностью считывания. В какой степени они подтверждены ошибками - совершенно неизвестно, и нет оснований ожидать каких-либо соотношений между их надежностями. Возможно также, что большинство ошибок совершается, когда ДНК находится в покоящемся состоянии, т. е. когда не происходит ни репликации, ни считывания.

Можно предложить еще следующий список вопросов:

1. Является ли процесс декодирования непосредственным переводом с языка нуклеиновых кислот на язык аминокислот или существуют промежуточные стадии?
2. Одинакова ли длина всех кодовых слов?
3. Не достигается ли синхронизация благодаря последовательному считыванию от одного конца цепи ДНК вплоть до другого?
4. Все ли земные организмы пользуются одинаковым кодом?

Ответы на все эти вопросы могут иметь важное значение для понимания процессов генетического кодирования. Интересно будет посмотреть, сколь много для окончательного решения этой проблемы смогут сделать математики, предсказав факты, не известные экспериментаторам, и насколько экспериментаторы смогут опередить математиков.

Литература

1. Golomb S. W., Welch L. R., Delbruck M., Construction and properties of comma-free codes; Biol. Medd. Dan. Vid. Selsk., 23, № 9 (1958). (Русский перевод: Голомб С. У., Велч Л. Р., Дельбрюк М., Строение и свойства кодов без запятой, Математика, 4 : 5 (1960), 137-160.)
2. Gamov G., Possible mathematical relation between deoxyribonucleic acid and proteins, Biol. Medd. Dan. Vid. Selsk., 22, № 2 (1954).
3. Crick F. H. C, Griffith J. S., Orgel L. E., Codes without commas, Proc. Nat. Acad. Set. USA, 43 (1957), 416-421.
4. Golomb S. W., Gordon В., Welch L. R., Comma-free codes, Canad. J. Math., 10 (1958), 202-209. (Русский перевод: Голомб С. У., Гордон Б., Велч Л. Р., Коды без запятой, Кибернетический сборник, вып. 5, ИЛ, М, 1962.)
5. Jaynes E. Т., Note on unique decipherability, IRE Trans, on Information Theory, IT-5, № 3 (1959), 98-102.
6. Recent results in comma-free codes; Research Summary 36-7, т. 1, стр. 44-45, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, Calif., 15 февраля 1961.
7. Paley R. E. A. C., On orthogonal matrices, J. Math. Phys., 12 (1933), 311-320.
8. Reed I. S., A class of multiple-error-correcting codes and the decoding scheme, IRE Trans, on Information Theory, IT-4 (1954), 38-49. (Русский перевод: Рид И. С, Класс кодов с исправлением нескольких ошибок и схема декодирования, Кибернетический сборник, вып. 1, ИЛ, М., 1960.)