
Приложение. Мера зацепленности. Ф. Б. Фуллер. Калифорнийский технологический институт, Пасадена, Калифорния
Для оценки степени зацепленности двух цепей можно использовать контурный интеграл Гаусса. Если С и С' - две ориентированные непересекающиеся замкнутые кривые в пространстве, то контурный интеграл Гаусса
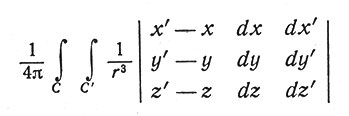
(где точка (x, y, z) лежит на С, а (x', y', z') - на С' и r = √((x' - x)2 + (y' - y)2 + (z' - z)2) ) является целым числом, равным взятому со знаком минус коэффициенту зацепления кривых С и С'. На рис. 1, а и 1, б изображены типичные примеры; на рис. 1, в показано, что две кривые могут быть зацеплены даже когда коэффициент зацепления равен нулю, а соленоид на рис. 1, г демонстрирует физический смысл интеграла Гаусса как работы по переносу единичного магнитного полюса по замкнутой кривой в магнитном поле, вызванном протеканием единичного электрического тока по другой кривой.
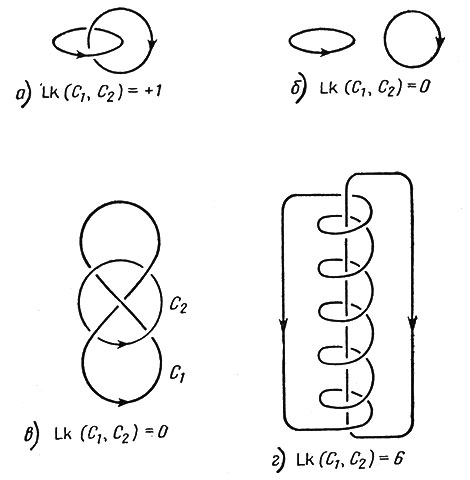
Рис. 1. Примеры пар кривых с соответствующими значениями связности. В случае (в) связность равна нулю, так как зацепленность можно устранить, пересекая кривую C1 ею же, а такое пересечение не отражается в интеграле Гаусса
Если непересекающиеся ориентированные кривые С и С' не замкнуты, то коэффициент зацепления для них никак не определяется. Тем не менее для таких кривых интеграл Гаусса сохраняет смысл и определяет действительную функцию С*С' двух кривых, обладающую следующими свойствами:
- С*С' не зависит от параметризации этих кривых, за исключением того, что обращение ориентации одной кривой влечет изменение знака величины С*С';
- С*С' = С'*С;
- С*(С1'+C2') = С*С1' + С*С2';
- С*С' инвариантна относительно переносов, вращений и гомотопии пространства, содержащего кривые С и С';
- если С и C' составлены из отрезков, как цепочки в модели Дельбрюка, то С*С' является непрерывной функцией расположения С и С';
- если кривые С и С' плотно намотаны одна на другую в виде двойной спирали с тысячью или более витков, то значение С*С' по существу равно числу витков. С другой стороны, если С и C' не зацеплены в интуитивном смысле, то значение С*С' обычно мало; в частности, если С и C' лежат в одной плоскости, то С*С' = 0.
Геометрическая интерпретация интеграла Гаусса в значительной мере помогает выявить его свойства. Зафиксируем кривую С', а кривую С перенесем в бесконечность движением Tλ, определенным в пространстве, содержащем С. (Здесь Т0 оставляет все точки пространства на месте, а изменение λ от нуля до бесконечности означает перенос кривой С в бесконечность.) Вообще говоря, некоторые из промежуточных кривых TλС должны иметь общие точки с кривой С', в то время как С не пересекает С'. Положим, что эти общие точки образуют конечное множество P1, P2,..., Pm и что в каждой точке Pi вектор L (касательная к TλС), вектор М (касательная к С') и вектор N (направление скорости движения Tλ) не лежат в одной плоскости. Пусть μi равно +1 или -1 в зависимости от того, образуют векторы (L, M, N) правую или левую тройку, и положим E(Tλ) = ∑mi=1μi. Тогда число E(Tλ) равно алгебраической сумме общих точек кривых TλС и С'. В общем случае Е(Тλ) зависит от Tλ, но если обе кривые С и С' замкнуты, то число Е(Tλ) является инвариантом движения Tλ и равно -Lk(C, С'). Определение числа Е(Tλ) проиллюстрировано на рис. 2. Движения Tλ,u, которые переносят С в бесконечность (здесь 0≤λ≤∞, а u - единичный вектор), являются смещениями, переводящими каждую точку х пространства в точку Tλ,u (х) = х + λu. Если С и C' - ломаные, то Е определяется для почти всех u; в этом случае можно показать, что интеграл Гаусса С*С' равен среднему значению величины E(Tλ,u) по единичной сфере, образованной концами векторов.
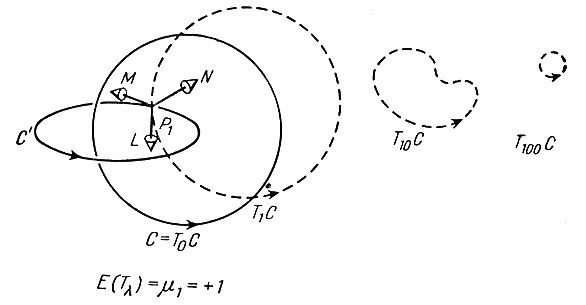
Рис. 2. Подсчет числа связностей между двумя кривыми С и С'; С' зафиксирована, а С перемещается в бесконечность. Показано несколько промежуточных положений. В одном из них кривые пересекаются в точке P1. Этому пересечению отвечает число +1, так как (L, M, N) - правая тройка векторов
Эта последняя интерпретация интеграла Гаусса дает возможность ввести упрощенную меру зацепленности: вместо усреднения Е(Tλ) по сфере направлений образуем среднее величин E(Tλ,j), отвечающих конечному множеству движений Tλ,1, Tλ,2 ..., Tλ, n. В случае цепей модели Дельбрюка, лежащих в кубической решетке, рассматривать сферу неудобно в силу ее изотропности. Более естественными были бы переносы в шести направлениях, определяемых единичными векторами ±(1,0,0), ±(0,1,0) и ± (0,0,1). Сначала для того чтобы избавиться от движений, для которых Е не определяется, имеет смысл сдвинуть С на один из восьми векторов вида (±1/2, ±1/2, ±1/2); тогда С попадет в кубическую решетку, дуальную к той, которая содержит С'. Затем Е можно усреднить по 48 движениям, которые соответствуют сдвигам в эту дуальную решетку и переносам, параллельным одной из осей координат; результат обозначим C▫C'.
Пусть S1 и S2 - два непересекающихся ориентированных отрезка этой кубической решетки, тогда S1▫S2 = 0, если только их проекции на одну из трех координатных плоскостей не образуют пару пересекающихся перпендикулярных отрезков. В этом случае S1▫S2 равно +1/24 или -1/24 в зависимости от того, является тройка (S1, S2, V) правой или левой (здесь V - вектор из любой точки отрезка S1 в любую точку отрезка S2). Это правило для двух отрезков применимо и для вычисления C▫C' любых двух непересекающихся цепей в кубической решетке, поскольку каждая цепь представляет собой сумму отрезков, а используя билинейность, можно разложить произведение C▫C' в удвоенную сумму произведений Si▫Sj' этих отрезков. Рис. 3 иллюстрирует расчет C▫C' для двойной спирали, состоящей из двух витков, а также для тех же самых двух цепей после сдвига одной из них на две единицы вправо. Рассматривая флуктуации величины C▫C' отвечающие описанным Дельбрюком перемещениям С и C' под влиянием броуновского движения, интересно отметить, что изменение C▫C' вызванное одним из элементарных переносов кривой С, равно B▫C', где В - малая замкнутая кривая, состоящая из измененного участка кривой С и его первоначального контура.
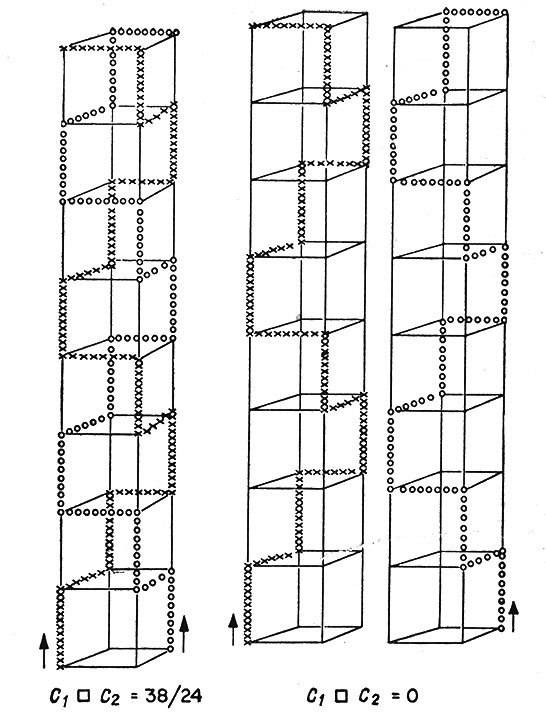
Рис. 3. Зацепление между двумя цепями, образующими двойную спираль с двумя витками, и теми же цепями, разделенными между собой. В первом случае E = 38/24, во втором E = 0. В общем случае для n витков E = 5n/6 - 1/12. В такой двойной спирали величина зацепления одного полного витка с одним полным витком другой спирали равна E0 = 18/24, если данные два витка расположены на одном и том же уровне; E1 = 1/24, если один виток смещен вверх или вниз относительно другого на шаг спирали, и E≥2 = 0 для смещений на два или более шагов
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'