
Проблема узлов в биологии. М. Дельбрюк. Калифорнийский технологический институт, Пасадена, Калифорния
Многие из разнообразных и высокоспециализированных функций живых организмов осуществляются с помощью молекул в форме цепи, причем длина этих молекул нередко очень велика по сравнению с их шириной. Для структуры таких молекул характерно наличие простых повторяющихся звеньев, образующих остов молекулы. К этим повторяющимся звеньям присоединены боковые группы, по одной к каждому звену, причем последовательность боковых групп может быть либо периодической, либо непериодической. В белках имеется около 20 различных боковых групп, так что такие цепи можно рассматривать как нечто похожее на сообщение, записанное при помощи английского алфавита. Это касается всех белков, выполняющих специфические функции катализаторов. Подобная конструкция этих цепей обеспечивает им возможность переплетаться весьма специфическим нерегулярным способом, в результате чего создается пространственная структура, обращенная к окружающей среде высокоспециализированной поверхностью, хорошо соответствующей конфигурации тех молекул, которые участвуют в катализируемой реакции. Можно сказать, что здесь мы имеем дело с конструкторской задачей, состоящей в специфическом заполнении трехмерного пространства одномерным материалом. В других белках, например в белках сухожильных или мышечных волокон, должна решаться другая задача; она состоит в построении макроструктур с заданными физическими свойствами: упругостью, пластичностью, электропроводностью и т. д. Нуклеиновые кислоты представляют собой другой класс соединений, молекула которых имеет вид длинной цепи и состоит из определенных единиц, повторяющихся вдоль осевой линии, и боковых групп, прикрепленных по одной к каждой такой единице. В этом случае существует только четыре типа боковых групп, находящихся друг с другом в таком же отношении симметрии, как четыре масти в колоде карт, где имеются две различные красные масти и две различные черные масти. Такие цепи поэтому более похожи на сообщения, записанные азбукой Морзе, а задачей, для выполнения которой предназначена такая структура, является хранение информации, точное ее удвоение и обеспечение "считывания" ее в соответствующее время.
Организаторы данного симпозиума обращали особое внимание приглашаемых докладчиков-биологов на выдвижение новых проблем, которые могли бы быть связаны с математикой. Мне кажется, что упомянутые выше проблемы образования узлов и переплетений принадлежат к этому классу, и мне хотелось бы обсудить их здесь. Я вовсе не уверен в том, что вводимые здесь математические идеализации соответствуют физической реальности и являются достаточно изящными или хотя бы последовательными. Для того чтобы решить эти вопросы, понадобится гораздо более глубокое исследование, чем то, результаты которого излагаются в этой статье.
Рассмотрим следующую модель молекулы, представляющей собой свернутую случайным образом длинную цепь. Пусть молекула состоит из N+1 бусин, связанных N жесткими стержнями единичной длины, так что общая, или контурная, длина данной молекулы равна N. Пусть в каждой бусине имеется шарнир, и пусть угол между двумя стержнями (валентный угол в реальной молекуле) равен 90°, а вся цепь "вписана" в кубическую решетку. Другими словами, следуя вдоль цепи, после прохождения каждого стержня мы встречаемся с необходимостью выбрать одно из четырех возможных направлений. Таким образом, здесь моделируется наличие фиксированного валентного угла, свободного вращения вокруг каждой из связей и выбора ориентации. При этом не допускается, чтобы две бусинки после прохождения некоторой петли оказались в одном и том же месте. Это в сущности означает, что цепь имеет некоторую толщину, равную длине одного звена.
Следует иметь в виду, что эта модель должна быть аналогом, а не копией реально существующих молекул в форме цепи. Ряд свойств нашей модели установлен до некоторой степени произвольно и носит искусственный характер. Так, например, реальная молекула может состоять из звеньев различной длины, чередующихся периодически. Кроме того, хотя валентные углы вообще фиксированы, они почти никогда не равны 90°; они больше походят на углы тетраэдра, равные 120°. Возможные повороты вокруг каждого звена могут быть ограничены больше, чем мы предполагали, например как в случае двойных связей, или меньше - как в случае одинарных связей. Далее, длина каждого звена не является строго фиксированной, но подвержена колебательным изменениям с очень высокой частотой, причем амплитуда колебаний, возможно, достигает 10%. Во всех этих отношениях наша модель идеализирует действительность, и любые выводы, которые мы можем сделать применительно к этой модели, представляют физический интерес лишь постольку, поскольку они не слишком сильно зависят от исходных допущений этой модели. Имея в виду эти оговорки, мы приступим теперь к проверке некоторых свойств модели и постановке интересующих нас задач.
Внутреннюю конфигурацию данной цепи можно описать ориентацией каждого звена lj относительно плоскости, образованной двумя предшествующими звеньями lj-1 и lj-2. В общем случае lj может иметь четыре ориентации с углами 0, π/2, π и 3π/2 (j = 3, 4, ..., N). Общую внутреннюю конфигурацию задают, фиксируя каждый из этих углов. В соответствии с правилом, запрещающим перекрытия, многие из комбинаций этих углов исключаются. Для того чтобы задать положение цепи в пространстве, достаточно задать координаты ее начала и ориентацию двух первых стержней.
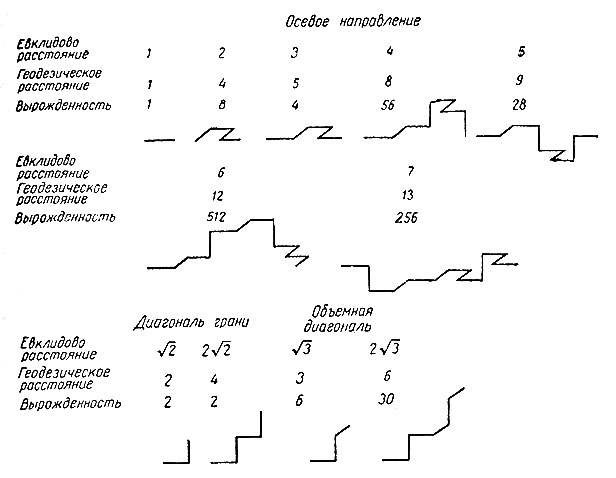
Рис. 1. Связи по геодезическим линиям. Приведены примеры связей между точками по осевым направлениям (верхний и средний ряды) и по диагоналям граней и объемным диагоналям (нижний ряд). Для каждой пары таких точек указаны евклидово расстояние, расстояние по геодезической линии и вырожденность. Заметим, что связи по диагоналям граней отличаются слабой вырожденностью (2) для любой длины и что вырожденность осевых связей немонотонно возрастает с длиной. Вырожденность каждого нечетного евклидова расстояния равна половине вырожденности предыдущего евклидова расстояния. Отметим значительное ее увеличение у связи по геодезической линии, соответствующей осевому расстоянию, равному 6
Следует заметить, что кратчайшее расстояние между двумя точками ("геодезическая линия") обладает некоторыми свойствами, которые могут показаться странными. Очевидно, что длина геодезической линии больше, чем длина прямой, но коэффициент удлинения очень сильно зависит от направления относительно осей той кубической решетки, в которую вписана цепь. Вдоль осей этот коэффициент примерно равен 2, вдоль диагоналей граней он равен √2, вдоль объемных диагоналей равен √3. Кроме того, эта геодезическая линия обладает большой степенью вырожденности, т. е. существует много линий (соединяющих данные вершины), имеющих минимальную длину. В то время как некоторые из этих геодезических линий как будто стремятся пройти от одного конца к другому по возможности прямо, другие из них удивительно "горбаты". Эти соотношения иллюстрируются табл. 1 и рис. 1. Среди длинных геодезических линий слабой вырожденностью обладает только та, которая образована диагоналями граней. Анизотропия, связанная с этим явлением, вызывает здесь больше всего затруднений. Такая анизотропия неестественна для модели, которая должна имитировать поведение длинных цепеобразных молекул в изотропном растворителе.
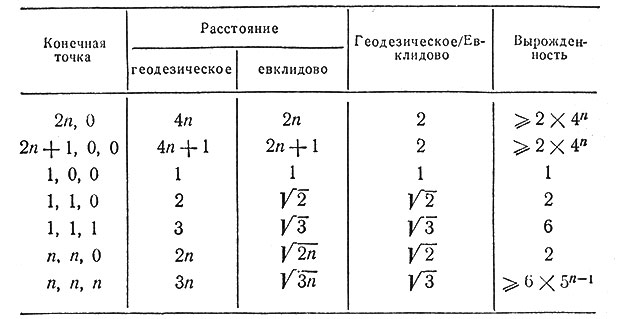
Таблица 1. Геодезические линии, связывающие начальную точку с точкой (m, n, p)
В дальнейшем нас будут интересовать главным образом вопросы образования узлов в пределах одной цепи и скручивания цепей друг с другом (зацепление), а также статистика этих конфигураций и скорости преобразований одних конфигураций в другие.
Начнем с простейшего вопроса, касающегося наличия узлов в отдельной цепи. Какая доля допустимых конфигураций цепи данной длины будет содержать узел? Конечно, с точки зрения топологов, правильным будет ответ: "никакая", так как наши цепи по определению незамкнуты и поэтому не могут быть заузлены в строгом топологическом смысле. Следовательно, топологическое определение оказывается слишком узким для наших целей, и нам надо прежде всего дать определение узла, соответствующее нашим целям. Мы можем условиться, что данная цепь содержит узел, если после соединения ее концов прямой линией она содержит истинный узел. Или мы можем условиться не соединять концы прямой линией, а продлить их до бесконечности. Первое из этих определений имеет то преимущество, что среднее расстояние между концами данной цепи примерно равно √N и, следовательно, для длинной цепи добавочное расстояние мало по сравнению с контурной длиной N. Таким образом, добавляются сравнительно небольшие цепи. В действительности, поскольку мы добавляем прямую линию, мы имеем не добавочную цепь, а новый, по существу чужеродный элемент. И все же удобнее, видимо, соединять концы прямой линией, а не геодезической, чтобы избежать той неопределенности, которую внесла бы вырожденность последней.
Минимальная длина модельной цепи, содержащей истинный узел, по-видимому, равна 36 (рис. 2), причем вырождение этой конфигурации оказалось слабым. Таким образом, конфигурации, содержащие узел, составляют лишь малую долю всех возможных конфигураций цепи длиной 36. Теперь рассмотрим цепь гораздо большей длины, например 10 000. Такая цепь может содержать большое число разнообразных узлов, а у каждого узла может быть любая "слабина" (или "свободная петля"), т. е. этот узел может захватывать участок любой длины, большей, чем минимальная, необходимая для образования узла. Поэтому наш первый вопрос будет касаться статистики этих узлов и особенно того, какова доля конфигураций, не имеющих узлов. Я не знаю ответа на этот вопрос, но предполагаю, что доля конфигураций без узлов довольно быстро стремится к нулю с ростом длины цепи.
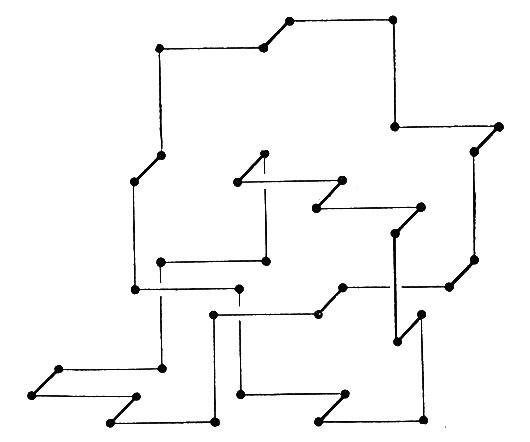
Рис. 2. Истинный узел. Длина этого узла равна 36 единицам. Можно считать, что эта длина является минимальной
Наш второй вопрос: как быстро будут завязываться и развязываться узлы в тех или иных условиях случайного движения? Для определенности мы снова должны сделать некоторые "модельные" предположения об этом случайном движении. Та модель, которую мы собираемся предложить, должна имитировать броуновское движение реальных цепей, а поведение этой модели представляет интерес лишь постольку, поскольку оно не слишком сильно зависит от ее специфических свойств.
Мы будем предполагать, что броуновское движение состоит из элементарных движений определенных типов; с помощью композиции и итерации этих движений можно получить любую из возможных конфигураций цепи и переместить ее в любую досягаемую часть пространства. Эти элементарные движения будут в каждый момент времени затрагивать возможно меньшее число звеньев. Мы будем классифицировать эти движения по числу звеньев, на которые они воздействуют.
1) Одно звено. Допустимо только для концевых звеньев. Вообще говоря, для каждого концевого звена существуют три возможных движения.
2) Два звена. Внутри цепи каждое движение затрагивает по крайней мере два звена, причем допускается только скачкообразный переход от одного угла квадрата к противоположному. Однако даже это движение допустимо только в том случае, если ни одно из двух звеньев a и b, смежных с рассматриваемой парой, не лежит в плоскости, образованной данной парой. Это иллюстрируется на рис. 3. Следовательно, если бы нам пришлось ограничить движение внутри цепи этими элементарными движениями двух звеньев, то большие участки цепи были бы достаточно жесткими и могли бы изменять свою конфигурацию только посредством движений, "заползающих" с концов. Поэтому целесообразно сделать еще один шаг и допустить элементарные движения, затрагивающие одновременно три звена. Такие движения можно классифицировать, исходя из начальной конфигурации рассматриваемых трех звеньев и звеньев, смежных с ними.
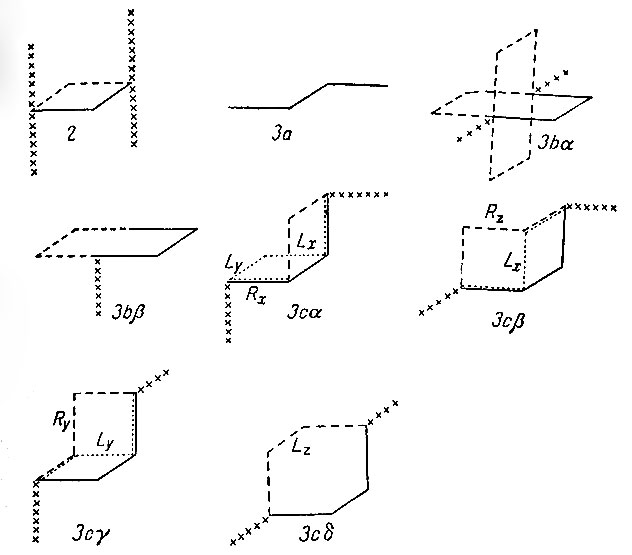
Рис. 3. Элементарные движения двух или трех звеньев. Показаны: исходная конфигурация (______), новые конфигурации (------) и смежные звенья (XXXXX)
3) Три звена.
a) Звенья лежат в одной плоскости, образуя зигзаг (рис. 3а). Движений нет: никаких других допустимых конфигураций для этих трех звеньев не существует.
b) Звенья лежат в одной плоскости, образуя выступ (рис. 3b).
α) Если а и b лежат в плоскости рассматриваемого триплета, то существуют три движения.
β) Если хотя бы одно из звеньев а, b не лежит в плоскости триплета, то возможно одно движение.
c) Рассматриваемые три звена не лежат в одной плоскости. Имеется шесть таких триплетов: три правых и три левых. Назовем их Rx, Ry, Rz, Lx, Ly, Lz. Пусть исходной конфигурацией будет Rx. Назовем звено а компланарным, если оно лежит в плоскости, образованной первыми двумя звеньями триплета. Аналогично назовем звено b компланарным, если оно лежит в плоскости, образованной последними двумя звеньями триплета.
α) Ни а, ни b не компланарны. В этом случае допустимы лишь переходы в состояния Lx и Ly, а эти переходы являются на самом деле переходами, затрагивающими только два звена.
β) Звено а компланарно, b не компланарно. Переходы в Rz и Lx, последний - движение двух звеньев.
γ) Звено а не компланарно, b компланарно. Переход в Ry и Ly, последний - движение двух звеньев.
δ) Оба звена а и b компланарны. Переход в Lz.
Определив элементарные движения, мы можем далее описать броуновское движение следующим образом: за время dt может произойти любое из перечисленных элементарных движений с вероятностью pidt, где коэффициент pi характеризует класс движений. Возможно, что этот коэффициент тем меньше, чем больше число звеньев, участвующих в движении.
Это определение случайного движения дает матрицу вероятностей переходов для всех конфигураций. Эта матрица симметрична и в основном состоит из нулей. Попутно заметим, что эта матрица - двоякостохастическая, а пространство конфигураций - эргодическое. Может возникнуть вопрос: является ли пространство конфигураций "неприводимым", т. е. можно ли из любого его участка попасть в любой другой участок? В некоторых случаях этого сделать нельзя. Например, если кубическая решетка, в которую вписана цепь, содержит "стенку" с небольшим отверстием, то могут существовать конфигурации, которые допустимы, но недостижимы; это те конфигурации, у которых цепь проходит через отверстие. Аналогичные конфигурации могут существовать в углах, ограничивающих имеющийся объем. Такие недостижимые конфигурации будут исключаться из общего объема пространства конфигураций. После этих исключений мы будем приписывать одинаковое значение терминам "объем в пространстве конфигураций" и "вероятность пребывания в данном классе конфигураций". В частности, мы вновь можем высказать предположение, что конфигурация длинной цепи, вероятно, содержит узлы. Тогда возникает новый вопрос: сколько времени нужно для того, чтобы на цепи мог завязаться или развязаться узел? Я не берусь ответить на него. Это время может быть очень большим, поскольку для изменения своей заузленности цепи приходится как бы проходить через довольно узкий перешеек в пространстве конфигураций. Возможно, что эта проблема связана с более простым вопросом о диффузном прохождении длинной цепи через узкое отверстие. Рассматриваемая проблема является более сложной, так как размер отверстия не фиксирован, а один из концов цепи как бы привязан к этому отверстию. Каждое из этих обстоятельств может сделать более вероятным развязывание узла, а не диффузию через отверстие.
Обратимся теперь к взаимодействию двух случайных цепей. Среднее расстояние между концами одной случайной цепи будет порядка N1/2. Рассмотрим две случайные цепи, вписанные в кубическую решетку с линейными размерами, достаточно большими, но не слишком, по сравнению с N1/2. Какова вероятность того, что произойдет скручивание двух заданных цепей друг с другом? Здесь нам вновь приходится модифицировать обычное топологическое определение зацепления. Мы снова можем сделать это, соединяя концы каждой цепи прямой линией и отыскивая после этого истинные зацепления*. Исходя из ранее сказанного об эргодических свойствах пространства конфигураций, ясно, что в состоянии равновесия цепи, по-видимому, не будут скручены. Это заключение противоречит, как может показаться некоторым, интуитивному представлению, основанному на следующем рассуждении: если цепи уже скручены, то прежде чем разойтись, они будут очень долго оставаться вместе, тогда как после расхождения они могут сравнительно свободно двигаться друг к другу и легко зацепиться при соприкосновении. Таким образом, может возникнуть предположение о большой вероятности зацеплений в состоянии равновесия. Это заблуждение частично обусловлено тем, что в нашей модели мы пренебрегаем силой трения между цепями. Более детальный анализ очень ясно показывает, что данным двум цепям одинаково трудно как зацепиться, так и расцепиться.
* (Проф. Фуллер предположил, что для получения меры зацепленности можно обобщить контурный интеграл Гаусса. Эта очень полезная идея развивается им в приложении к этой статье.)
Теперь нас интересует вопрос: сколько нужно времени для того, чтобы коэффициент зацепления мог измениться в том или ином направлении? И снова я не берусь делать предположения. Похоже, что эту проблему можно исследовать экспериментально, путем изучения вязкости. Здесь зацепление между молекулами должно быть показателем некоторого дополнительного взаимодействия, отличного от гидродинамического, которому до сих пор уделяли исключительное внимание. Взаимодействие, основанное на зацеплении, должно сильно зависеть от скорости сдвига, и эта зависимость может служить показателем скорости изменения зацепления.
Эта последняя проблема уже немного приближает нас к реальным молекулам. Нуклеиновые кислоты, несущие генетическую информацию, имеют любопытную форму двойных цепей, причем эти цепи закручены одна вокруг другой в виде правильной двойной спирали с ты* сячью и более витков. Эта двойная спираль обладает достаточной жесткостью и практически нулевой энтропией; при каждом делении клетки она подвергается репликации. Как нам кажется, это происходит следующим образом: две цепи отходят одна от другой, после чего каждая цепь дополняется в результате синтеза новой комплементарной цепи. Иными словами, происходят организованные процессы расцепления и повторного зацепления. Существенно, чтобы этот процесс происходил с большой скоростью и надежностью, с минимальным износом и без разрывов цепи. Недостаток знаний о том, как это происходит in vivo, не позволяет нам построить правдоподобную модель, на основании которой можно было бы делать расчеты. In vitro, т. е. в пробирке, возникает более простая ситуация. Некоторые воздействия, а именно высокая температура, повышенная кислотность или некоторые химические реакции, вызывают распад цепей. Любое из этих воздействий преодолевает те слабые силы притяжения, удерживающие две цепи вместе, без которых эта конфигурация не могла бы существовать. Когда эти силы устранены, то при условии, что пространство, в котором размещены двойные спирали, достаточно велико, цепи должны разойтись, и они действительно расходятся. Ни эксперимент, ни теория в настоящее время не могут адекватно справиться с проблемой скорости этого расхождения. Эксперимент показывает, что цепи, несомненно, могут быстро приходить в состояние, в котором зацепление мало, если не отсутствует полностью. Однако данные, представленные для доказательства того, что это расцепление происходит быстро, неудовлетворительны. Было бы желательно иметь в руках теоретический аппарат, который позволил бы выяснить, с какой скоростью может происходить зацепление или расцепление. Вопрос о разделении двух цепей рассматривается в теоретических работах [1] и [2]. В работе [1] предполагается, что разделение происходит следующим образом. Сначала двойная спираль ослабляется по всей длине путем раскручивания, скажем ста из тысячи всех ее витков. Предполагается, что при этом отдельные цепи теряют свою жесткость, обеспечивавшуюся плотностью закручивания, и они могут путем диффузии свободно отделяться друг от друга в продольном направлении. Наоборот, в работе [2] предполагается, что при разделении двух цепей большая часть двойной спирали не раскручивается, а распутывание начинается на обоих концах. Распутанные части образуют на каждом конце две неправильные спирали, вращающиеся одна вокруг другой. Преодоление вязкости при вращении происходит за счет высвобождения энергии. Каждое распутанное звено переходит из жестко закрепленного состояния в состояние довольно свободного вращения.
По причинам слишком сложным, чтобы обсуждать их здесь, ни одно из этих описаний способа раскручивания двух цепей нельзя считать соответствующим действительности. Трудности определения правильного способа не столько математические, сколько физические. Не хватает знания некоторых параметров, особенно относительной величины сил, связывающих цепи в поперечном и продольном направлениях. Как только эти параметры станут лучше известны, задачу можно будет поставить математически, и тогда вопрос зацепления будет играть значительную роль. В работах же [1] и [2] проблема зацепления в общем виде не рассматривалась.
Литература
- Kuhn W., Zeitbedarf der Langsteilung von miteinander verzwirn-ten Fadenmolekulen, Experientia, 13 (1957), 301-307.
- Longuet-Higgens M. C, Zimra В., Calculation of the rate of uncoiling of the DNA molecule, J. Molec. Biol., 2 (1960), 1-4.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'