Биохимия для математиков-бесплодная пустыня или целина? Артур Парди. Калифорнийский университет, Беркли, Калифорния

I. Математика в биохимии. В этой статье мы покажем, какого рода проблемы существуют в биохимии, и выделим те из них, которые могли бы представлять интерес для математиков. Мы рассмотрим два вопроса: есть ли в биохимии системы, представляющие математический интерес, и могут ли в настоящее время математики внести полезный вклад в биохимию. Как видно из этих вопросов, математиков в биохимии могут привлекать две различные цели; при этом математик обычно не может одновременно сделать ценный вклад и в математику, и в биохимию.

Образование и интересы у математиков и биохимиков весьма различны. Большинство биохимиков, например, вряд ли хорошо владеет школьным курсом алгебры, а большинству математиков, вероятно, не известны структурные и функциональные различия между белками и нуклеиновыми кислотами. Однако некоторые из биохимиков получили математическое образование, а кое-кто из математиков изучал биологию (см., например, [10] и [14]). Между этими дисциплинами существует лишь слабая связь, но можно надеяться, что со временем она будет крепнуть.

В настоящее время трудно перекинуть мост между математикой и биохимией. Конечно, биохимики все время пользуются простейшим математическим аппаратом - арифметикой, алгеброй и кое-чем из дифференциального исчисления. Прикладные математические методы, причем иногда довольно сложные, использовались для изучения физических свойств биологических молекул, и особенно макромолекул. Однако многочисленные расчеты поведения сложных биологических систем не дали практически ничего для биохимического понимания явлений. Возможно, математика могла бы внести фундаментальный вклад в анализ сложных процессов, в изучение экономики роста, в проблемы оптимизации и в описание статистических свойств, общих для всех биохимических систем. Решать эти вопросы должен, пожалуй, не биохимик, а математик, имеющий представление об общих принципах биохимии.

Настоящая статья написана с точки зрения биохимика. Мы начнем с описания основных проблем "чистой" биохимии - области, в которой большинство математических приложений мало эффективно. Затем перейдем к рассмотрению сложных систем реакций и их поведения, представляющих интерес благодаря нелинейности и наличию обратной связи. Закончим рассмотрением возможного математического подхода к изучению таких систем, основанного на постулате: система формируется таким образом, что максимизируется скорость ее роста. Математик легко представит себе трудности, стоящие перед автором при изложении этого материала, если вообразит себя пишущим аналогичную статью для биохимиков.

II. Структурная биохимия. Конечная цель биохимии состоит в описании жизненных процессов в химических терминах. Удобно разбить биохимию на следующие три раздела: 1) природа химических веществ, 2) реакции, переводящие одни вещества в другие, и 3) интеграция реакций в единое функциональное целое. Первый из этих разделов тесно связан с физической органической химией. Он изучает различные группы химических веществ, встречающихся в живых организмах, и свойства этих веществ. Из растений, животных и бактерий были выделены тысячи различных соединений, определены их структура и свойства. Размеры их молекул - от нескольких атомов (различные сахара) до десятков тысяч атомов (белки и нуклеиновые кислоты). Эти последние представляют собой комбинации меньших молекул, компоновка которых в настоящее время является предметом интенсивного изучения.

Выделение биохимических соединений само по себе не порождает математических проблем, но при попытке описать эти соединения с учетом их взаимодействия с различными физическими факторами, например светом или силовыми полями, такие проблемы уже появляются. Математики-прикладники, рассматривая такие взаимодействия, обычно просто распространяют на них результаты классической механики и гидродинамики. Примером может служить определение структуры веществ методом дифракции рентгеновских лучей; определение формы молекул по вязкости, изучение взаимодействия спиральных структур в поляризованном свете, а также изучение флуоресценции и передачи энергии между молекулами, поведения молекул в электрическом поле и при центрифугировании (см. работы [14, 20]).

Такого рода математические методы определения структуры соединений достаточно хорошо разработаны и в большинстве случаев позволяют правильно интерпретировать наблюдения. Когда биохимическая проблема требует математического решения, оно находится, и лимитируют здесь данные биохимии, а не возможности математики.

III. Ферменты и обмен веществ. Вторая из упомянутых проблем биохимии - превращение одних соединений в другие - относится к динамическому аспекту. Какие происходят превращения и каковы их химические механизмы? В основе динамической биохимии лежат два общих положения. Первое: практически каждая биохимическая реакция катализируется каким-нибудь ферментом. Даже такая простая реакция, как реакция двуокиси углерода с водой

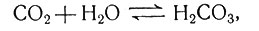
может быть ускорена особым ферментом. Правда, эта реакция протекает достаточно быстро и без фермента, но большинство химических реакций в отсутствие специфического фермента протекает с едва заметной скоростью. В настоящее время идентифицировано около 1000 ферментов и около 100 ферментов получено в очищенном виде. Все ферменты являются белками. Выяснение механизмов каталитической активности ферментов - одна из самых увлекательных проблем современной биохимии. Были предприняты попытки математического рассмотрения этого вопроса с точки зрения квантовой механики (например, [18]); однако представления о механизме катализа, основанные на физической и органической химии, по-видимому, еще не настолько развиты, чтобы было целесообразно широкое математическое изучение.

Математические методы часто пытались применить для изучения скоростей превращения одних соединений в другие. При описании элементарной кинетики катализа биохимики часто пользуются уравнением Михаэлиса, основанным на модели, в которой фермент и субстрат (реагирующая молекула) объединяются, а затем диссоциируют на исходный или измененный субстрат (продукт реакции) и неизменный фермент:

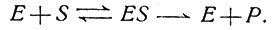
(1)

Уравнение для стационарного состояния (при ^d[ES]/_dt = 0 и [E]<<[S]) таково:

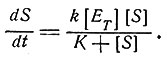
(2)

Здесь [S] и [E_T] - концентрация субстрата и суммарная концентрация фермента соответственно, t - время, а k и K - константы. Учение о кинетике катализа было значительно развито и обобщено в работах [19, 8]. Вообще говоря, для каждого субстрата считают справедливой кинетику первого порядка. Скорости обратных реакций обычно считаются пренебрежимо малыми. Трудности при описании кинетики появляются в тех случаях, когда в реакции участвуют несколько субстратов, или когда реакция обратима, или когда рассматривается переходная кинетика, или же когда присутствуют соединения, влияющие на активность ферментов (активаторы или ингибиторы). Прежде чем приводить какие-либо расчеты биохимических процессов, необходимо быть уверенным, что методы измерений позволяют получить надежные результаты. Кинетические исследования, проводимые на целом организме или в системах с неочищенными ферментами, во многих случаях трудно интерпретировать.

Второе важное общее положение динамической биохимии: всякое сложное изменение состоит из ряда последовательных простых реакций. Каждая простая реакция катализируется отдельным специфическим ферментом и приводит лишь к небольшому изменению субстрата - обычно к разрыву какой-либо одной химической связи и образованию новой связи между другими атомами. Возникновение сложных молекул из простых происходит не скачкообразно, а в результате постепенного изменения структуры. Даже реакции, которые кажутся простыми, могут происходить в несколько этапов. Например, при образовании из молекулы сахара двух молекул молочной кислоты

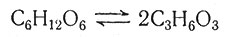
шестиуглеродная цепь сахара разрывается пополам и происходит перегруппировка атомов кислорода и водорода. Это достаточно сложный процесс; он состоит по крайней мере из И отдельных реакций, каждая из которых катализируется своим ферментом. Такая сложность не является результатом несовершенства и своенравия природы; напротив, она обеспечивает эффективный способ освобождения энергии реакции и образования промежуточных продуктов, которые могут стать исходными субстратами для новых реакций.

В течение последних тридцати лет было потрачено много усилий на изучение последовательностей реакций в живых тканях. Большинство основных путей теперь уже хорошо обследовано. Некоторые из них представляют собой линейные последовательности реакций, другие разветвляются, а изредка встречаются и циклические реакции; при этом продукт является одним из двух субстратов для исходной реакции и вовлекается в нее повторно (рис. 1).

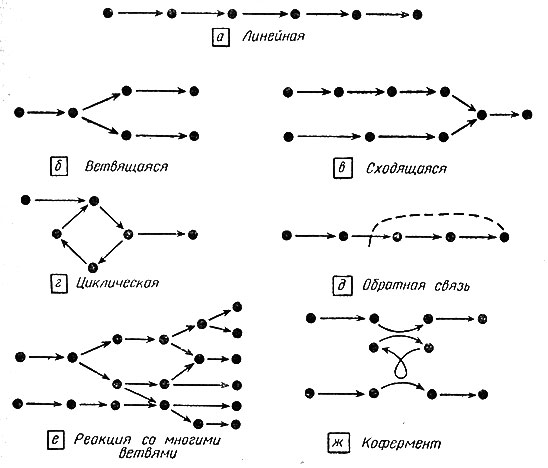
Рис. 1. Возможные типы биохимических реакций

Изучение кинетики такого рода последовательностей реакций часто проводилось с математической точки зрения. Первый фермент использует ресурсы системы и поставляет субстрат для второго фермента. Продукт второго фермента обеспечивает исходным материалом третий фермент и т. д. Задача состоит в описании потока веществ в зависимости от количественных характеристик компонентов системы. Такие открытые системы рассматривались достаточно часто (см. [3]). Исследовались как стационарные состояния, так и переходные процессы, вызванные различными изменениями.

Прежде чем рассматривать суммарную реакцию, рассмотрим подробнее ее отдельные стадии. Скорость каждой элементарной реакции зависит от двух факторов. Один из них - концентрация молекул фермента, катализирующего эту реакцию. Мы будем пока считать суммарную концентрацию фермента фиксированной. Другой фактор - зависимость скорости от концентрации субстратов. В первом приближении считают, что если в ре^ акции участвуют два субстрата, то один из них присутствует в избытке и его концентрация не ограничивает скорости. Учитывают лишь изменение концентрации другого: считают, что оно описывается уравнением Михаэлиса. (Случаи, когда три субстрата участвуют в одной реакции, встречаются редко.) Еще одним важным фактором является влияние ингибиторов на активность ферментов. Некоторые продукты, образующиеся под действием ферментов в одной части цепи реакций, являются ингибиторами для других ферментов.

Торможением по типу обратной связи называют торможение активности одного фермента продуктом деятельности другого фермента, катализирующего одну из последующих реакций (см. рис. 1, д). В случае торможения по типу обратной связи синтез может прекратиться, если скорость синтеза данного продукта превышает скорость его удаления из системы. Таким способом предотвращается перепроизводство данного соединения. Этот механизм весьма полезен в живых системах. Хорошим примером служит синтез пиримидинов - составных частей нуклеиновых кислот (см. [24]). В этом случае образование конечного продукта из более простых исходных веществ происходит в результате 8 последовательных реакций. Этот конечный продукт является ингибитором первой реакции как в интактной клетке, так и в очищенных системах. Торможение по типу обратной связи было обнаружено фактически во всех основных путях биохимических превращений, в которых его искали. Действие ингибиторов проявляется очень быстро, по-видимому потому, что комплекс фермент - ингибитор очень похож на комплекс фермент - субстрат, но уже не участвует в дальнейших превращениях.

Еще один способ взаимодействия различных реакций можно наблюдать, когда субстратом для некоторого фермента являются конечные продукты двух других реакций. Возможно также, что два фермента, участвующие в двух различных реакциях, используют в качестве субстрата одно и то же соединение; при этом возникает конкуренция (см. рис. 1, е и ж). Ряд специфических задач возникает при рассмотрении циклических систем, которые могут входить в качестве составных частей в те или иные метаболические пути (рис. 1, г).

Эти открытые системы можно рассматривать как сильно идеализированные модели систем реакций, протекающих в живой клетке. Такие модели наиболее применимы в тех случаях, когда ростом клетки можно пренебречь. Одним из больших преимуществ моделей биохимических систем является то, что их поведение в новых ситуациях относительно нетрудно исследовать (по сравнению, например, с экономическими моделями). Методы изучения потока веществ в различных реакциях несложны. Например, радиоактивные соединения, поглощаемые организмом, вовлекаются в те же реакции, что и аналогичные соединения, не обладающие радиоактивностью (см. [2]). А поток радиоактивных соединений и размеры фондов радиоактивных промежуточных продуктов во многих случаях определяются без труда [3, 21].

Всегда в таких случаях приходится постоянно учитывать степень надежности биохимических данных. Существует много способов постановки эксперимента, но большинство из них некорректны. На результаты биохимических реакций в сложных системах могут влиять многочисленные неизвестные факторы. Кроме того, кинетические данные не могут доказать, что модель выбрана правильно; другие модели могут дать те же результаты. В лучшем случае они могут лишь отвергнуть гипотезу.

Результаты теории кинетики открытых систем недавно были использованы для изучения конкретной биохимической системы, осуществляющей разложение глюкозы на двуокись углерода и воду. Была разработала упрощенная схема этой реакции [4], включающая 21 стадию, для описания которых нужно соответствующее число уравнений. С помощью цифровой вычислительной машины были обработаны необходимые данные и получены графики зависимости концентраций компонентов от времени; результаты оказались вполне удовлетворительными и подтвердили качественные представления о взаимодействиях между частями этой системы. Кроме того, стало ясно, какие большие усилия требуются для разрешения такой проблемы. Лишь очень немногие системы изучены настолько подробно, чтобы была возможна подобная работа по их моделированию.

При синтезе гигантских молекул, таких, как белки или нуклеиновые кислоты, из большого числа составляющих их субъединиц должно быть координировано множество отдельных реакций. Достаточно широкого изучения математических вопросов, связанных с биосинтезом полимеров, пока еще не проводилось.

Математические методы применялись для изучения воздействия ферментов на большие молекулы. Здесь может, например, представлять интерес вопрос, разрывает ли фермент связи внутри молекулы хаотически или упорядочение от одного конца молекулы к другому [1].

IV. Координация реакций. Третий раздел биохимии изучает, каким образом отдельные цепи реакций складываются в общую картину того, что происходит в живой клетке. Наиболее подходящим объектом для такого изучения являются бактерии - с ними проще всего работать. Хотя бактерии и состоят из единственной клетки с очень небольшими размерами (несколько тысячных миллиметра), они невероятно сложны с биохимической точки зрения. Многие бактерии могут из единственного соединения, такого, как сахар, и некоторых неорганических веществ синтезировать все несколько сотен соединений, необходимых для размножения делением. Необходимые реакции протекают с невероятными скоростями: некоторые бактерии могут создать себе подобных менее чем за 20 минут. В бактериальной клетке каждую минуту подвергаются изменениям несколько сот миллионов молекул. Эффективность и точность этих реакций несравнимы с тем, что достигнуто человеком. Высоко-координированные системы реакций, гибко приспосабливающиеся к изменениям окружающей среды, выдвигают проблемы качественного изучения механизмов их координации, а в итоге - и количественного их изучения.

При переходе от отдельных реакций к изучению функционирования клетки в целом возникают следующие три осложнения. Первое - одновременно происходит множество реакций. Многие реакции начинаются с какого-нибудь компонента среды или же ответвляются от какой-нибудь промежуточной стадии других реакций. Общая схема будет похожа на джунгли, где реакции представлены ветвящимися деревьями, увешанными лианами, которые соединяют разные ветви. Конечными продуктами являются в основном гигантские молекулы - белки и нуклеиновые кислоты. Координация реакций осуществляется, по-видимому, на тех стадиях, где конвергируют несколько реакций. Быстро синтезируемые вещества небольших размеров не могут быть включены в гигантские молекулы раньше, чем будут готовы более медленно синтезируемые вещества. Это связано с тем, что различные вещества используются в определенных пропорциях. Избытки продуктов накапливаются, а их синтез тормозится по типу обратной связи [15].

Для создания математической модели сложной системы множественных реакций можно считать, что в каждой последовательности реакций есть одна, скорость которой лимитирует скорость всей системы. Такие реакции, лимитирующие суммарную скорость, можно включить в модель наряду с торможением по типу обратной связи.

При некоторых условиях клетки могут расти, и это является вторым осложняющим обстоятельством. Продукты реакций могут поставлять новый клеточный материал, в том числе ферменты, так что система с течением времени увеличивается в объеме. Качественное исследование растущих систем широко проведено в работе [16]. Одним из результатов роста является разбавление старых продуктов новыми. Некоторые количественные аспекты этого вопроса рассмотрены в статье [16а].

Третье осложнение - это повышенная концентрация некоторых веществ внутри живой клетки по сравнению с окружающей средой. Эта разница в концентрациях обусловлена наличием клеточных барьеров, препятствующих свободной диффузии молекул. Концентрация веществ в клетке зависит как от концентрации его во внешней среде, так и от относительных скоростей его поступления и выведения из клетки и происходящих химических реакций. Особый интерес представляет активный перенос, "накачивающий" некоторые вещества внутрь клетки; благодаря ему концентрация вещества внутри клетки может во много раз превышать наружную концентрацию. Некоторые из ферментов, обеспечивающих механизм активного переноса (называемые пермеазами), образуются только в присутствии веществ, подлежащих переносу. Говорят, что такое вещество индуцирует образование пермеаз. В результате появляется так называемый эффект памяти: клетки, подвергнутые воздействию высоких концентраций индуцирующего вещества, могут в течение некоторого времени после этого реагировать на такие низкие концентрации, какие ранее не могли быть использованы. Кратковременное воздействие высоких концентраций вещества индуцировало образование пермеазы, которая и обеспечивает нагнетание этого вещества внутрь клетки, например бактериальной. Математическое изучение образования эффекта памяти и его длительности проведено в работе [13], где рассматривается пример, иллюстрирующий положение о том, что живые клетки могут находиться более чем в одном относительно стабильном реакционноспособном состоянии, но переходы между ними осуществляются лишь при специальных условиях [7].

V. Изменения количества ферментов. Скорость синтеза многих ферментов определяется концентрациями в клетке некоторых небольших молекул. Здесь имеют место два тесно связанных процесса: индукция и репрессия. Индукция - это специфическая стимуляция образования фермента каким-либо веществом, например субстратом, изменяемым под влиянием фермента. Репрессия - это подавление синтеза фермента некоторым специфическим веществом, обычно одним из продуктов реакции. Влияние индукторов и репрессоров может быть довольно сильным. Они могут изменить концентрацию фермента более чем в 1000 раз. Следовательно, скорости отдельных этапов в цепи биохимических реакций могут сильно зависеть от степени индукции или репрессии и, следовательно, от количеств индукторов и репрессоров, синтезируемых на других этапах реакции.

И торможение по типу обратной связи, и репрессия - все это проявления обратной связи, но их не надо путать: в первом случае подавляется активность фермента, а во втором - его образование (см. рис. 2).

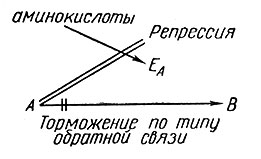
Рис. 2

В некоторых случаях добавление какого-либо одного компонента к питательной среде может запустить новую реакцию, состоящую из нескольких этапов. Это явление известно под названием последовательной индукции: добавленное вещество индуцирует появление фермента Е_А, который превращает это вещество в продукт В, а В индуцирует появление фермента Е_B, который превращает В в С, и т. д. (см. [22]).

Влияние индукторов и репрессоров проявляется довольно быстро: уже через несколько минут концентрация фермента начинает изменяться. Однако равновесная концентрация достигается лишь спустя несколько часов. Аналогично, если удалить индуктор, концентрация фермента вернется к первоначальной (благодаря разбавлению при росте) очень нескоро.

Первые попытки математического описания таких явлений были сделаны в работах [9] (индукция) и [23] (репрессия). Хотя эти математические работы основаны на моделях, которые, возможно, неточны в деталях, они служат основой для сравнения с опытными данными, а также подсказывают новые эксперименты.

VI. Кинетические модели метаболических систем. Математическое описание процесса роста клетки - одна из существенных проблем, и ей посвящены многочисленные работы. Обычно в них используется кинетический подход; модель состоит из набора ферментов, некоторым образом связанных с субстратами, фонды которых конечны. Относительно числа молекул фермента делаются либо самые общие предположения, либо указываются конкретные числовые значения для моделирования некоторой определенной системы. Связи между ферментами осуществляются через идеализированные последовательности реакций, например линейные, или выбранные согласно некоторой схеме, как в работе [4], где делается попытка по возможности точно, хотя и схематично, представить часть процессов обмена веществ. Считая, что действия ферментов подчиняются основным законам, таким, как уравнение (2), можно математически описать свойства системы. Свойства таких систем обсуждаются в работе [3]. Однако в большинстве случаев эти модели носят, по-видимому, слишком общий характер, чтобы с их помощью можно было получить глубокие представления о функциях клетки.

В работе [6] описывается рост клетки в терминах кинетической модели, в которой скорость увеличения концентрации каждого из ферментов пропорциональна концентрации некоторого другого фермента:

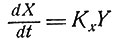
и т. д. Там показано, что такая система стремится к состоянию, в котором каждая компонента нарастает экспоненциально. Общая скорость роста всей системы максимальна. Интересно было бы проследить, в какой степени поведение этой системы зависит от предположения, что скорость роста каждой компоненты пропорциональна концентрации лишь одного из метаболитов. Каково будет поведение системы, если, согласно уравнению Михаэлиса,

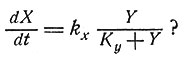
При любых ли начальных условиях система будет стремиться к возможно более быстрому экспоненциальному росту? Если скорость образования каждого фермента регулируется с помощью репрессий, то основное уравнение должно иметь вид

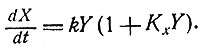
А как ведет себя такая система? До сих пор еще не делалось попыток построить модели, отражающие известные способы взаимодействия ферментов.

VII. Модели, максимизирующие метаболизм. В этом разделе мы хотим предложить новый подход к изучению метаболизма, отличный от ранее использованного кинетического. Мы сформулируем постулаты, которым Должна подчиняться система, и выведем из них ее свойства. Именно такой подход используется в термодинамике: законы термодинамики утверждают, что энергия сохраняется, а энтропия возрастает. Из этих термодинамических законов выводятся далеко идущие следствия, имеющие как научное, так и прикладное значение. Приложимость этих следствий к реальным явлениям основана, конечно, на справедливости законов термодинамики. Можем ли мы аналогичным образом изучать свойства живых систем, исходя из некоторых общих законов?

Для растущих систем часто постулировалось свойство максимизировать тот или иной из параметров, определяющих систему. Интуитивно эта концепция кажется вполне приемлемой, а справедлива она или нет, необходимо проверять опытным путем. Возможно минимизировать потери, максимизировать производство энергии, энтропию или скорость ее возникновения. В работе [17] исследуется термодинамика необратимых процессов и показывается, что в стационарном состоянии скорость роста энтропии открытой системы минимальна. Возможно, это условие выполняется и для биохимической системы в целом, включая и скорости образования в ней ферментов. Однако расчеты здесь производить довольно трудно.

Микроорганизмы, по-видимому, сочетают способность к быстрому росту при оптимальных условиях с гибкостью реакций на изменения внешней среды. Многие бактерии, перенесенные в лабораторию из своей естественной среды, условия которой подвержены значительным колебаниям, обычно хорошо растут при самых разных условиях. Они обладают механизмами индукции, репрессии и торможения по типу обратной связи, и с помощью этих механизмов регулируют содержание в клетке многих ферментов, способность к синтезу которых заложена в них генетически. Другие микроорганизмы, обнаруживаемые, например, в молоке или в живых тканях, значительно более требовательны к условиям роста. Эти организмы не обладают некоторыми из ферментов, необходимых для синтеза важных соединений; которые они обычно получают из окружающей среды. Однако они могут обладать другими приспособлениями для выживания (например, образование спор или выделение токсинов), которые хотя и снижают временно скорость роста, но создают преимущества для роста этих организмов в течение длительных сроков.

В этой статье предлагается относительно простой и интуитивно привлекательный подход. Мы прежде всего постулируем, что максимизируется скорость роста, т. е. скорость, с которой увеличивается общая масса сбалансированного набора конечных продуктов метаболической системы. Это предположение вполне оправдано для клеток, число которых непрерывно возрастает, например для бактерий, так как в условиях борьбы за существование смогли выжить и пройти естественный отбор лишь наиболее быстро размножающиеся организмы. Действительно, такой естественный отбор можно продемонстрировать в лаборатории. Поместив организмы в условия, отличные от естественных, можно наблюдать появление новых организмов (мутантов) с измененным характером метаболизма (см. [5, 12]).

На систему необходимо наложить некоторые ограничения. Мы предположим в качестве граничных условий, что общее число молекул фермента в клетке не может превышать некоторого уровня: в бактериальной клетке может быть размещено лишь конечное число молекул фермента, так как каждая молекула занимает конечный объем. Задача состоит в выборе числа молекул ферментов каждого типа в такой пропорции, которая обеспечила бы максимальную скорость роста.

Можно ввести граничные условия и по-другому, считая фиксированной скорость роста или скорость производства конечного продукта, и таким образом ограничить сверху число молекул фермента. Такой подход может быть полезным при рассмотрении нерастущей клетки или подсистемы, которая должна обеспечивать поступление некоего компонента в более сложную систему. Например, таким образом можно рассматривать реакции, задачей которых является снабжение клетки энергией со скоростью, в точности обеспечивающей потребности клетки. Если существуют альтернативные пути производства энергии, высвобождающие различное количество энергии при разных условиях, как в системе, рассмотренной в работе [4], то такая система, поставляющая необходимое количество энергии в зависимости от условий, может обеспечивать минимальное общее число молекул фермента.

Идеализированная система должна состоять из n ферментов и запасов одного или нескольких исходных веществ. В результате последовательных реакций эти исходные продукты превращаются в промежуточные, а потом и в конечные продукты обмена, которые существуют внутри клетки в виде пулов различных концентраций. Удельная скорость превращения каждого метаболита в следующий должна зависеть от концентрации этого метаболита, концентрации молекул фермента, катализирующего реакцию, и некоторых других факторов, таких, как ингибиторы. Допускается возможность некоторой утечки каждого метаболита в окружающую среду, в результате чего происходит известная потеря веществ в системе. Конечные продукты также уходят из системы; в растущей системе они превращаются в пропорциональное количество новых клеток.

Используя указанные выше постулаты и граничные условия, можно рассчитать концентрации различных ферментов, скорости синтеза каждого из промежуточных и конечных продуктов, а также утечку веществ из системы.

Это можно проиллюстрировать следующим простым примером. Предположим, что исходное вещество N с помощью фермента Е_n превращается в метаболит А, а А превращается в конечный продукт Z с помощью фермента E_a. Концентрация промежуточного вещества А в системе обозначается через [А]; его утечка из клетки происходит со скоростью v_q = [A]q, пропорциональной концентрации вещества А. Пусть скорости синтеза вещества А из N и Z из А будут равны соответственно v_n и v_a:

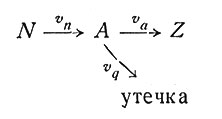
Согласно уравнению Михаэлиса (2), при [N]<<K_n и [A]<<K_a имеем

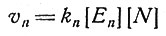
(3)

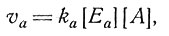
(4)

где [E_n] и [Е_a] - концентрации обоих ферментов. Должно выполняться условие

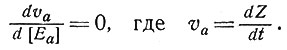
(5)

Необходимо максимизировать скорость синтеза вещества Z, изменяя соотношение количеств ферментов так, чтобы

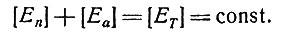
(6)

В установившемся состоянии, т. е. при d[A]/dt = 0, должно установиться равновесие между синтезом вещества А и его расходом. Тогда

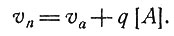
(7)

Из этих уравнений можно определить значения [E_n] и [E_a], удовлетворяющие уравнениям (5) и (6), если с помощью исключения переменных представить v_a как функцию от [E_a] и выполнить дифференцирование. Получим

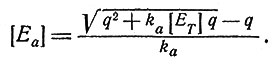
Можно определить и другие параметры, т. е. [E_n], v_n, v_a, v_q и [A].

Эту элементарную модель можно усложнить, чтобы она точнее отражала действительные биохимические процессы. Можно увеличить число реакций (см. рис. 1). Наиболее непосредственное усложнение модели состоит в увеличении длины линейной цепи реакций (рис. 1, а). Каждая отдельная реакция должна иметь свой собственный фермент, свой фонд исходных продуктов и свои скорости их расходования. Необходимо максимизировать конечную скорость по отношению к величинам [E_i]. Другой случай представляют ветвящиеся цепи (рис. 1, б), начинающиеся с одного и того же исходного вещества и выдающие много различных продуктов, синтезируемых различными дивергентными последовательностями реакций (рис. 1, е). Количества конечных продуктов должны получаться в таких пропорциях, чтобы для всех продуктов Z_i≥αZ_i⁰, где Z_i - константы, а коэффициент α должен быть максимизирован.

Реакции, протекающие в клетке, могут быть гораздо сложнее; некоторые типичные усложнения показаны на рис. 1. Нередко метаболит образуется в результате соединения двух ранее существовавших метаболитов (рис. 1, б). Или же два метаболита изменяются в процессе одной и той же реакции, а затем один из них вновь возвращается в исходное состояние, вступая в реакцию с третьим метаболитом (рис. 1, ж). Это характерно для коферментов, которые осуществляют связь между реакциями различных путей биосинтеза. Возможны также и другие усложнения: петли (рис. 1, е), активация или торможение продуктами других реакций (рис. 1, д), циклы (рис. 1, г) и системы, нуждающиеся в нескольких исходных веществах. Правила максимизации сложных систем, вероятно, можно сформулировать в терминах максимизации подсистем. Для этих задач можно использовать методы линейного программирования. Другой вопрос для таких систем - выяснение их общих свойств безотносительно к месту локализации всевозможных усложнений.

Некоторые типы реакций встречаются не часто. Например, участие более двух метаболитов или образование более двух конечных продуктов в реакции с единственным ферментом - явления редкие. Относительно некоторых веществ, таких, как вода, обычно предполагают, что их влияние на скорость реакции не меняется в процессе реакции, так как они находятся в избытке. Хотя обычно два реагента, вступая в реакцию, дают два конечных продукта, часто не принимают во внимание один из двух реагентов или один из продуктов, или даже одновременно и реагент и продукт.

Свойства живых систем также вносят некоторые модификации. Суммарная емкость растущей системы увеличивается пропорционально количеству образовавшихся продуктов. Кроме того, при изменении размеров клетки меняется отношение ее поверхности к объему. Если считать скорость диффузии питательных веществ в клетке и скорость выведения продуктов обмена пропорциональными поверхности клетки, то условие деления клетки можно сформулировать следующим образом: деление произойдет, если две клетки будут расти быстрее, чем одна, имеющая тот же суммарный объем.

Весьма интересно было бы также проследить за изменением концентрации [E_i] ферментов при изменении концентрации одного или нескольких питательных веществ. Если концентрации питательных веществ быстро изменяются, то каковы средние концентрации ферментов, обеспечивающие в среднем наиболее быстрый рост? Способствует ли торможение по типу обратной связи более быстрому в среднем росту клетки? Торможение по типу обратной связи должно приводить к увеличению скорости роста в условиях понижения концентраций питательных веществ.

Всякое регулирование требует затрат. Торможение по типу обратной связи даже при не слишком высоких скоростях реакции несколько подавляет активность фермента. Следовательно, для обеспечения той же скорости реакции в оптимальных условиях чувствительные к торможению ферменты должны присутствовать в больших концентрациях, чем нечувствительные. Кроме того, известен конкретный фермент, который в условиях торможения по типу обратной связи даже сам по себе является менее эффективным, чем при отсутствии такого торможения; для него коэффициент k в уравнении (3) при наличии торможения уменьшается процентов на пятьдесят. Интересно, окупается ли столь высокая цена торможения по типу обратной связи в тех случаях, когда метаболиты поступают медленно, как например, при синтезе коферментов.

Проблема затрат при регулировании имеет параллели и в деловом мире. Появившееся недавно "приглашение" подписаться на один широко известный журнал содержало следующие строки: "Пожалуйста, извините нас..., если Вы уже являетесь нашим подписчиком. Настоящее приглашение разослано согласно спискам, которые мы не в состоянии постоянно проверять и вычеркивать имена тех, кто уже успел подписаться". По-видимому, разослать больше приглашений дешевле, чем проверить списки.

Основная часть энергии в клетке заключена в молекулах аденозинтрифосфата (АТФ). Производство энергии можно отразить в схеме метаболизма, включив в нее реакции, оканчивающиеся синтезом АТФ. Для избыточного синтеза АТФ потребовалось бы больше фермента, чем для его синтеза в оптимальных количествах. Следовательно, максимальное производство энергии вряд ли может соответствовать максимальной скорости роста. Существуют ли какие-нибудь общие свойства у систем, максимизирующих скорость роста? Есть ли соответствие между быстрым ростом и высокой экономичностью системы на клеточном уровне? Потери в клетке происходят в результате утечки промежуточных продуктов, а также из-за производства конечных продуктов в количествах, избыточных по сравнению с тем продуктом, производство которого минимально.

Реакции, осуществляющиеся в бактериях, значительно сложнее, чем описанные здесь. Например, при повышении поступления питательных веществ бактерии не только растут быстрее, но и имеют большие средние размеры и большую концентрацию веществ (рибону-клеопротеидов), необходимых, как считают, для синтеза ферментов (см. [11]). Следует также рассмотреть системы, в которых скорость роста связана с изменением отношения поверхности к объему (и зависящим от него изменением потока веществ из клетки и в клетку и изменением скоростей реакций). Чтобы подобрать правильное соотношение между ферментами и производительностью ферментообразующих механизмов, необходимо принимать во внимание, кроме этих факторов, еще и скорость роста и общую концентрацию ферментов.

VIII. Выводы. Математические методы могут принести пользу биохимии. Обычно такие методы применяются тогда, когда в них возникает реальная потребность. Если же математические методы остаются без применения, то это происходит либо потому, что биохимия, по-видимому, не настолько еще развита, чтобы ее задачи можно было сформулировать математически, либо потому, что эти математические результаты не могут быть проверены опытным путем. Необходимо помнить, что биохимия - это в основном экспериментальная наука, где всякую систему, подлежащую изучению, можно легко изменить и затем проследить влияние таких изменений. Поэтому биохимики обычно предпочитают прямую проверку любой гипотезы построению моделей для расчетов. Для математиков, занимающихся прикладными вопросами, такая экспериментальная гибкость биохимии является несомненным преимуществом, делающим привлекательным построение соответствующих математических моделей и облегчающим проверку этих моделей.

Сотрудничество биохимиков и математиков, по-видимому, сможет оказаться ценным, если будут разрабатываться важные для современной биохимии проблемы. В конечном счете мы, биохимики, хотели бы описать основные принципы своей науки - науки об основах жизни - в математических терминах. Но я считаю совершенно невероятным, чтобы этот математический подход в ближайшем будущем занял центральное место в биохимическом мышлении или в биохимическом языке. Однако по мере того, как данные биохимии смогут все более точно отражать основные количественные свойства живой материи, будут укрепляться и ее связи с математикой, в основном усилиями заинтересованных лиц. Но уже и сейчас математики могут найти в биохимии ожидающие их любопытные проблемы, особенно в области сложных способов взаимодействия реакций.

Резюме. В статье рассматриваются общие проблемы биохимии и указываются случаи применения математических методов. Особенно полезным оказалось применение математики для изучения взаимодействия молекул со светом и различными силовыми полями. Математика оказалась полезной и при исследовании кинетики реакций, катализируемых ферментами. Кинетическими методами, а в самое последнее время - с помощью вычислительных машин были исследованы сложные регулируемые системы многочисленных взаимодействующих реакций в живой клетке.

В статье предлагается новый подход для математического описания систем реакций. Это по существу тот же подход, который используется в термодинамике. Приводится основной постулат и граничные условия, касающиеся глобальных свойств биохимических систем; из них выводятся параметры отдельных систем и константы индивидуальных реакций. Постулат: растущая система организуется так, чтобы максимизировать свою скорость роста. Граничные условия состоят в том, что клетка может содержать лишь конечное число молекул ферментов. Согласуются ли с опытом полученные отсюда результаты, еще предстоит проверить. В настоящее время могут быть исследованы некоторые математические проблемы, связанные с применением этих идей к различным гипотетическим системам.

Литература

1. Bailey J. M., French D., J. Biol. Chem., 226 (1957), 1.
2. Bassham J. A., Kirk M., Biochim. et Biophus. Acta, 43 (1960), 447.
3. Bray H. G., White K., Kinetics and thermodynamics in biochemistry; New York, 1957.
4. Chance В., Garfinkel D., Higgins J., Hess В., J. Biol. Chem., 235 (1960), 2426.
5. Cohen-Bazire G., Jolit M., Ann. Inst. Pasteur, 84 (1953), 937.
6. Dean A. C. R., Hinshelwood С. N., Progr. Biophys. and Biophys. Chem., 5 (1955), 1.
7. Delbruck M., Unites biologiques douees de continuite gene-tique; Paris, 1949, стр. 33.
8. Hear on J. Z., Bernhard S. A., Friess S. L., Botts D. J., Morales M. F., The enzymes, New York, 1959, т. 1, 2-е изд., стр. 49.
9. Heinmets F., Herschman A., Bull. Math. Biophys., 23 (1961), 69 и 227.
10. Lotka A. J., Elements of mathematical biology. New York 1956.
11. Neidhardt F. C, Magasanik В., Biochim. et Biophus, Acta, 42 (I960), 99.
12. Novick A., Szilard L., Dynamics of growth processes, Princeton, New York, 1954, стр. 21.
13. Novick A., Weiner M., A symposium on molecular biology, Chicago, III, 1959, стр. 78.
14. Oncley J. L., Schmitt F. O., Williams R. C, Rosenberg M. D., Bolt R. H., Biophysical science -A study program, New York, 1959.
15. Pardee А. В., The enzymes, New York, 1959, т. 1, 2-е изд., стр. 681.
16. Perret С. J., J. Gen. Microbiol., 22 (1960), 589.
17. Perret С. J., Levey H. C., J. Theoret. Biol., 1 (1961), 542.
18. Prigogine I., Introduction to thermodynamics of irreversible processes, Springfield, III, 1955.
19. Pullman A., Pullman B.,( Proc. Nat. Acad. Sci. USA, 45 (1959), 1572.
20. Reiner J. M., Behavior of enzyme systems, Mineapolis, Minn., 1959.
21. Schachman H. K., Williams R. C., The viruses, I, New York, 1959, стр. 223.
22. Solomon A. K., Mineral metabolism, New York, 1960, стр.119.
23. Stanier R. Y., Bacteriol Revs., 14 (1950), 179.
24. Szilard L., Proc. Nat. Acad. Sci. USA, 46 (1960), 277.
25. Yates R. A., Pardee А. В., J. Biol. Спет., 221 (1956), 757.