
Изучение лермановской модели диффузии и поглощения экситонов в ДНК. Вальтер Гоад. Калифорнийский университет, Лос-Аламос, Нью-Мехико
Несколько лет назад профессор Леонард С. Лерман из Колорадского университета высказал предположение, что некоторые из полученных им экспериментальных результатов по инактивации ДНК ультрафиолетом можно объяснить диффузией экситонов. Он предложил детальную модель, и я согласился посмотреть, можно ли из этой модели получить результаты, согласующиеся с экспериментом. В отношении физических принципов лежащих в основе модели, предстоит еще многое сделать, но я надеюсь, что расчет следствий из этой модели будет представлять некоторый интерес и как одно из приложений математики к биологии.
Лерман и Толмач [1], работая с пневмококками изучали влияние облучения ДНК ультрафиолетом на некоторый генетический признак (устойчивость к различным лекарственным препаратам). Они обнаружили, что вероятность сохранения признака не уменьшается экспоненциально с увеличением дозы. Один из полученных экспериментальных результатов приведен на рис. 1. По-видимому, часть ДНК, контролирующая изучаемый признак, не является простой мишенью для фотонов ультрафиолетовых лучей. При других повреждающих воздействиях, в том числе и при воздействии рентгеновскими лучами, вероятность сохранения признака зависит от дозы почти экспоненциально. Из этих данных Лерман заключил, что за этот признак отвечает участок с размерами около одной десятой средней длины молекулы ДНК у пневмококков.
![Рис. 1. Вероятность выживания сегмента ДНК в зависимости от дозы облучения ультрафиолетом согласно модели Лермана. Данные экспериментов взяты из работы [1]](pic/000289.jpg)
Рис. 1. Вероятность выживания сегмента ДНК в зависимости от дозы облучения ультрафиолетом согласно модели Лермана. Данные экспериментов взяты из работы [1]
В этих экспериментах использовалось излучение с длиной волны, соответствующей сильному резонансному поглощению на изолированных нуклеотидных основаниях. В молекуле ДНК эти основания расположены на расстоянии около 3,6 Å друг от друга в виде двойной спирали; поглощение ультрафиолетового излучения такой сложной электронной системой представляет собой довольно запутанное явление. В частности, из-за взаимодействия соседних оснований энергия возбуждения благодаря поглощению кванта в принципе не может быть локализована на одном основании, поскольку существует вероятность передачи возбуждения (или "экситона") с одного основания на другое.
Модель Лермана приближенно описывает поведение такой структуры. Предполагается, что экситоны случайно возникают в молекуле ДНК и исчезают, причем их энергия преобразуется в тепло или в энергию химических превращений, что приводит к биологической инактивации того сегмента молекулы, в котором расположен поврежденный участок. Далее предполагается, что в части поврежденных участков повреждение таково, что этот участок превращается в ловушку для экситонов,- любой попавший сюда экситон обязательно рассеивает свою энергию.
Все время от момента образования до момента поглощения или исчезновения экситонов происходит их диффузия: предполагается, что длина свободного пробега экситона равна λs для рассеивания и λa для поглощения; для нахождения распределения поврежденных участков по длине молекулы решается одномерное уравнение переноса. Пусть расположение участков вдоль молекулы приближенно описывается параметром l, и пусть N(l)dl - вероятность того, что экситон будет поглощен на участке (l, l + dl). Уравнение переноса в этом случае имеет вид
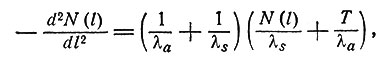
(1)
где Т - вероятность возникновения экситона на единицу длины. Если ловушки находятся в точках с координатами li, i = 1, 2, ..., n, то на концах каждого сегмента мы имеем граничные условия
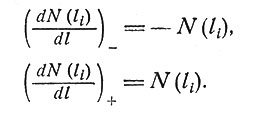
(1')
Для удобства будем считать, что те же самые граничные условия выполнены и на концах молекулы.
Эти предположения вполне правдоподобны, однако никаких более сильных утверждений в настоящее время высказать нельзя. Именно ловушки обеспечивают своеобразное поведение вероятности выживания, защищая соседние с ловушкой участки от дальнейшего повреждения. Данные по радиационному повреждению сцинтиллирующих материалов были интерпретированы подобным же образом [2]. Можно говорить о диффузии экситонов, обусловленных наличием оснований, если пренебречь квантовомеханическими взаимодействиями между ними. Для рассматриваемой задачи это будет хорошим приближением, так как можно предполагать, что в решении получится в явном виде затухание корреляций по фазе при переходах между состояниями упругих колебаний системы, включающей в себя основания вместе с их окружением.
Теперь мы будем рассматривать вероятность того, что некоторый участок молекулы ДНК, по предположению ответственный за изучаемый признак, не поврежден при облучении данной дозой ультрафиолета. Вероятность повреждения сегмента абсорбированным фотоном зависит от расстояния в каждом направлении до ближайших ловушек, так что мы имеем случайный процесс, в котором осуществляются переходы между состояниями системы, определяемой переменными l и r - расстояниями до ближайших ловушек. Поскольку мы будем использовать численные методы, будем считать, что l и r принимают лишь дискретные значения, для удобства целые. Введем следующие обозначения:
G - длина рассматриваемого сегмента;
L, R - начальные значения величин l, r;
p(l, r, τ) - вероятность того, что сегмент остался неповрежденным после дозы τ, а ближайшие ловушки, или концы молекулы, расположены на расстояниях l и r;
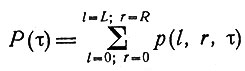
- суммарная вероятность выживания нашего сегмента;
q(m|m') - вероятность на единицу дозы возникновения новой ловушки на расстоянии m' от конца на сегменте, ограниченном ловушками (или концами молекулы) с расстоянием m.
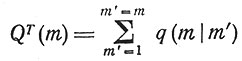
- суммарная вероятность на единицу дозы появления ловушки на сегменте длины m;
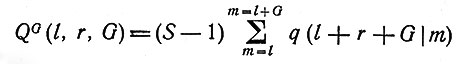
- вероятность на единицу дозы инактивации сегмента длины G без появления ловушки; S - отношение числа всех случаев инактивации к числу случаев образования ловушек.
Вероятность g(m|m') пропорциональна интегралу от соответствующего решения уравнения (1), взятому по интервалу m'≤;≤m'+1. После соответствующей нормировки (константы считаем включенными в определение единицы дозы) получим
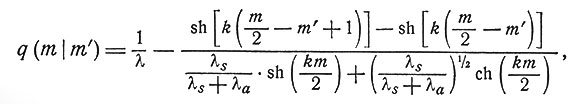
где
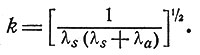
Теперь процесс описывается дифференциально-разностным уравнением:
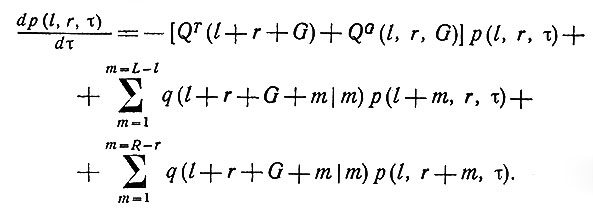
(2)
Мы проинтегрировали это уравнение на машине ИБМ-704 для многих наборов значений параметров λs, λa, L, R и G. Результаты оказались слабо зависящими от λs и λa при λs<G, λa/λs>1 что физически является вполне разумным диапазоном. На рис. 1 изображены для G = 5, R = L = 20 графики функции P(τ) - вероятности выживания сегмента размером в одну девятую длины молекулы, расположенного в ее центре. Видно, что при S (число случаев инактивации на одно образование ловушки) около 8 эти кривые обнаруживают качественно то же поведение, что и экспериментальные кривые.
Литература
- Lerman L. S., Tolmach L. J., Biochim. et Biophys. Acta, 33 (1959), 371.
- Rosenstock H. В., Schulman J. H., J. Chem. Phys., 30 (1959), 116.
- Hardwick E. R., McMillan W. G., J. Chem. Phys., 26 (1957), 1463.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'