Математические методы интерпретации электрокардиограмм. М. А. Вудбери, Л. Д. Кэди. мл. Нью-йорский университет, Нью-Йорк

Введение. Электрокардиограмма (ЭКГ). Ритмические сокращения мышечных волокон сердца сопровождаются возникновением электрических потенциалов, создаваемых большим числом перемещающихся диполей; эти потенциалы могут быть зарегистрированы с поверхности тела с помощью парных или множественных электродов. Линейная комбинация разностей электродных потенциалов называется "потенциалом отведения"; совокупность электродных потенциалов также представляет интерес, однако регистрировать можно только их разность.

Надо отметить, что в норме потенциалы отведения представляются функцией, которая близка к периодической. При измерении частоты пульса функция V(L, t), описывающая зависимость потенциала от времени в данном отведении, меняется определенным образом. Это изменение вызывается физической нагрузкой, утомлением, недостатком кислорода, изменениями состава электролитов плазмы крови и т. д. Несомненно, существуют индивидуальные различия между здоровыми людьми одного и того же пола, а также различия, зависящие от пола. Кроме того, существуют изменения, связанные с возрастом, с различными отклонениями от нормы и с болезнями.

Сейчас врачи-кардиологи для классификации и диагностики сердечных заболеваний используют запись потенциалов определенных отведений, так называемую электрокардиограмму с 12-ю стандартными отведениями. Обычно здесь возникают затруднения, связанные с различным расположением сердца у худых и полных людей, что приводит к различиям в графиках регистрируемых напряжений.

Сравнительно недавно был разработан новый метод электрокардиографического исследования - векторная электрокардиография. Этот метод основан на предположении о том, что электрическую активность сердца можно хорошо описать, рассматривая сердце как диполь с изменяющимися направлениями и величиной тока. Тогда каждый потенциал отведения можно достаточно полно представить скалярным произведением постоянного вектора отведения на переменный дипольный вектор. Заметим, что суммарный диполь сердца вызывает такое пространственное распределение потенциала на поверхности тела, которое несколько отличается от распределения, приписываемого иногда "дипольной гипотезе". Согласно этой гипотезе, такое распределение соответствует направлению электродов от центра в сердце в пространство снимаемых сигналов. А следовательно, линейное пространство потенциала отведений является точно трехмерным, т. е. справедлива "гипотеза трех функций".

Однако поскольку на самом деле система трех функций представляет собой лишь некоторое приближение к действительности, никакая из "дипольных гипотез" не может описать истинную физическую картину явления. Хорошо известно (Гельмгольц), что одна и та же картина распределения потенциалов на поверхности тела может. соответствовать бесконечному множеству различных распределений диполей внутри этого тела. Поэтому можно утверждать, что никакие описания или интерпретации распределения потенциалов на поверхности тела, вообще говоря, не вскрывают физической природы источников электрических потенциалов в сердце. В заключение надо подчеркнуть, что в данной работе мы ограничимся анализом электрокардиограмм с точки зрения их описания и классификации и не будем касаться физической стороны дела.

Диагностика и классификация. Электрокардиограмма (ЭКГ) используется для диагностики заболеваний и пороков сердца обычно в сочетании с данными медицинского обследования, наследственности, истории болезни и с другой информацией (применяемые методы лечения и т. п.). При таком использовании определенные показатели ЭКГ являются "диагностическими". Например, по форме зубцов Q_III и T_III^* можно поставить диагноз инфаркта задней стенки при наличии таких клинических симптомов, как стойкие сильные боли в области сердца, иррадиирующие в левую руку, и повышение содержания глутамат-оксалат-трансаминазы в сыворотке от 30 ед. (в норме) до 400. Здесь решающим фактором является форма комплекса Q_III - T_III. Остальная информация не может служить основанием для диагноза инфаркта задней стенки; она лишь указывает на наличие инфаркта миокарда. Чаще всего ЭКГ является подтверждением клинической картины заболевания. Особое значение в форме ЭКГ придается таким факторам, как понижение сегмента S - T, заострение и увеличение зубцов Р, возникновение различных аритмий, например экстрасистолы, и многое другое.

^* (Большой зубец Q и инвертированный зубец Т в III отведении.)

Математическое описание этих элементов ЭКГ и их изменений, определение границ нормы и отклонений от нормы в зависимости от возраста, пола, метода лечения, истории болезни и т. д. представляют собой интересную и трудную проблему. Такое описание необходимо для эффективного использования вычислительных машин для обработки получаемой информации и как средства для диагностирования заболевания.

Современные исследования в этой области (включая "и исследования авторов) ведутся в направлении автоматизации установления тех параметров электрокардиограммы, которые врачами и исследователями в прошлом были признаны полезными. Разрабатываются машинные программы, которые будут определять эти параметры для исследовательских и стандартных систем отведений. Например, существующая программа для машины ИБМ-650 менее чем за минуту обрабатывает данные одного сердечного цикла, полученные при одном отведении. Более быстродействующие машины даже без дополнительных усовершенствований смогут обрабатывать сигналы от системы с 12 стандартными отведениями в реальном масштабе времени. Конечно, результирующий поток информации будет необозримым и высоко избыточным. Далее, разработанная нами машинная программа позволяет только быстро и точно "измерять" параметры ЭКГ и обеспечивает весьма незначительный анализ данных, воспринимаемых "без разбору".

Можно наметить два направления для дальнейших исследований. Одно направление состоит в том, чтобы определить те правила, которыми обычно пользуются при постановке диагноза крупные электрокардиологиклиницисты, и дать математическое описание исследования параметров ЭКГ согласно этим правилам. Ясно, что такой путь чреват опасностями, особенно если результаты будут применяться для назначения лечения без наблюдения со стороны компетентного кардиолога, который понимает, какой результат может выдать машина, а также осознает ограниченность любой "замороженной" системы правил подобного типа. Не исключено, однако, что, несмотря на возможные опасности и серьезную оппозицию, дальнейшие исследования пойдут в первую очередь именно в этом направлении.

Другое направление заключается только в проведении измерений, необходимых для выполнения машинного анализа параметров ЭКГ, а не для постановки диагноза, как выше. В этом направлении для выявления существенных сторон информации, получаемой клиницистом или исследователем, гораздо нужнее математический анализ. Та информация, которой сейчас пользуются на практике, отчасти интуитивна, очень сложна и большей частью трудно поддается строгому описанию, и это не страшно. Но информация, которая явится результатом математической обработки, должна быть выдана клиницисту четко в различных формах, но не должна быть жестко интерпретирована, так как ясно, что ее интерпретация изменяется в зависимости от достижений теории и практики. Кроме того, в программе, предназначенной для обработки информации, должна предусматриваться возможность выявления ошибочных и, если возможно, неверно снятых данных (например, неправильное расположение электродов, неверные данные об обследуемом пациенте и т. д.).

В основе этого подхода лежит предположение, что если возможно восстановить данные, представленные потребителю (в нашем случае - клиницисту), до исходного вида, то вся "информация" сохраняется в некоторой системе суммарных величин.

Для дальнейшего развития этого направления в качестве основного положения было выдвинуто положение о "выделимости" образа. Ряд исследователей понимает анализ и распознавание образов как создание некоторой классификации, необходимой для установления категорий и создания метода (алгоритма) отнесения образа к одной из этих категорий. Этот подход заменяет правила, которыми пользуется клиницист, более обширной и объективной системой правил.

Если в клинической практике будет применен этот метод анализа и обработки информации, то врачу останется наряду с остальными обязанностями использовать полученные результаты. В первую очередь этот подход преследует практические задачи. Можно почти с уверенностью сказать, что, во-первых, мало кто отличит этот путь решения проблемы от первого направления, рассмотренного выше, и, во-вторых, на этом пути обычно часть избыточной информации, подаваемой на вход, теряется.

В результате краткого знакомства с проблемой примем, что она может быть решена, если удастся создать наиболее удачную систему сжатого представления информации в ЭКГ в том смысле, что результат обработки может быть использован для восстановления картины работы сердца с заданной точностью. Грубо говоря, мы предлагаем осуществить это путем составления своего рода "атласа" образов. Тогда количественные значения определенных параметров (соответствующих данному образу) работы сердца предопределят ЭКГ и исходные данные могут быть восстановлены по этим значениям с заданной точностью. Если для группы больных имеется ряд диагнозов, полученных на основе клинических наблюдений, то степень и природу связи диагноза и параметров ЭКГ можно определить с помощью методов линейного или нелинейного дискриминантного анализа или множественного регрессионного анализа, как, например, в работе [7].

Предполагается, что информация будет представляться в машину в канонической математической форме. По представленной таким образом информации путем добавления составных частей можно будет восстанавливать картину работы сердца. При необходимости клинического использования результаты будут выдаваться в соответствующей форме, определяемой специалистами.

Анализ полученных результатов. Представление новой информации в некоторой канонической форме влечет за собой необходимость создания нового способа ее расшифровки. С помощью метода аналогий было показано, что графики, "восстановленные" в результате обработки описываемым методом, поддаются клинической расшифровке, если в качестве базиса используются три независимых отведения [4, 5]. Для того чтобы элементы ЭКГ в уже понятной кардиологу форме могли служить для диагностики (в сочетании с другими клиническими данными), необходимо произвести некоторый предварительный анализ, и может оказаться, что большая часть существенной информации содержится вовсе не в электрических потенциалах, зарегистрированных на ЭКГ.

В этих предварительных рассуждениях предполагается, что изучается один человек, который находится в физиологически устойчивом состоянии - обычно в состоянии покоя. Однако иногда кардиологу приходится иметь дело со случаями отклонения оси сердца или так называемой "декстракардии", когда сердце находится в правой половине грудной полости. Естественно, что при этом записи потенциалов в 12 стандартных отведениях представят необычную картину. В таких случаях восстановление истинной картины (нормальной или патологической) может занять некоторое время, поскольку даже в норме, скажем, максимальное отличие будет проявляться не в обычном отведении. Некоторые тесты, например тесты на выносливость при физической нагрузке, построены на сравнении ЭКГ, снятых до и после выполнения упражнений. Форма ЭКГ изменяется и различна для разных людей. Природа этих изменений такова, что одна и та же система трех функций не может описать ЭКГ и до и после проведения теста. Отсюда следует необходимость описать ЭКГ в более точных терминах, а для этого очень важно изучать ЭКГ людей с известными отклонениями и снятые в самых различных условиях. Некоторые изменения, появляющиеся с возрастом или после начала болезни, уже изучены, но все еще не решены проблемы, связанные с представлением и со снятием нужной информации. Очень дорога аппаратура, используемая для сбора, регистрации и анализа экспериментальных данных, но без нее нельзя ни разработать методы сбора данных, ни проверить математический аппарат.

Математическое рассмотрение. Как уже указывалось, любая линейная комбинация разностей потенциалов между парами электродов на поверхности тела S называется потенциалом отведения V(L, t). Здесь временная зависимость выступает в явном виде. Такое понимание отведения, несмотря на трудности, которые оно ставит перед человеком, не имеющим математической подготовки, имеет большое значение для унификации теории, из него непосредственно следует, что система возможных отведений образует линейное пространство, а при добавлении понятия ортогональности (или скалярного произведения)-векторное пространство. Однако это не есть векторное пространство векторной кардиограммы, а возникающее здесь понятие ортогональности отведений является одним из принципиальных источников недоразумений в этом вопросе. Далее заметим, что потенциалы отведений можно складывать, умножать на скаляры и находить обратные и что существует нулевое отведение, так что если принимать результирующие разности потенциалов за потенциалы для нового отведения, то для отведений определяются обычные операции в векторном или линейном пространстве.

Важно определить эквивалентность отведений, и это мы делаем, обращаясь к векторной функции Шмитта преобразования импеданса или к полю отведения Мак-Фи. Следуя Шмитту [6], мы видим, что вектор m момента диполя, расположенного в точке р области сердца Я, вносит составляющую Z^T(L, p)m, где Z^T(L, p) - транспонированная вектор-строка функции преобразования импеданса в точке р, а m - вектор-столбец. Будем считать два отведения эквивалентными, если они описываются одинаковыми функциями преобразования импеданса. Существование Z(L, р) зависит от линейности среды, но не от ее изотропности или однородности.

Теперь важно рассмотреть "идеальные отведения", т. е. отведения, для которых Z(L, р) не зависит от положения р диполя в области Н (отличной от самого сердца, так как сердце движется внутри области Н), а также не зависит от времени. Следовательно, векторная функция преобразования импеданса для идеальных отведений L сводится к Z(L), а потенциалы отведений теперь выражаются формулой

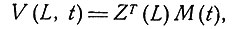
где M(t)-общий или суммарный (по Н) вектор момента сердечного диполя в момент времени t. Заметим, что M(t) никак не локализован, так как идеальные отведения строятся таким образом, чтобы они были независимы от положения диполя; поэтому смещения сердца внутри области H не влияют на M(t). Говорить об ортогональности идеальных отведений имеет смысл потому, что они однозначно соответствуют векторам Z, направления которых хорошо определяются как направления внутри тела и величины которых также легко определяются. В случае неидеальных отведений понятие ортогональности не вводится.

Существует самое большее три линейно независимых идеальных отведения, обозначаемых X, Y и Z и направленных по трем осям тела, которые определяются симметрией и приблизительно цилиндрической формой грудной клетки. X направлено горизонтально влево, Y - вниз и Z - назад. Представив каждое такое отведение через единичные импедансы, введем обозначения

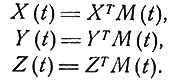
Вместо X, Y и Z можно для удобства использовать обозначения X₁, X₂ и X₃. Временной след вектора

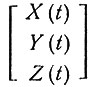
мы называем идеальной векторной кардиограммой. Подобную систему, отличающуюся только масштабными коэффициентами при X, Y и Z, представляет собой система отведений Шмитта - Симонсона SVEC-III.

Понятие ортогональности как понятие, относящееся к физическим направлениям, теряет смысл, если отведения не идеальны. Конечно, если два отведения L₁ и L₂ таковы, что Z(L₁, p) и Z(L₂, p) некоторого диполя везде ортогональны в области сердца, то мы можем назвать такие отведения ортогональными, но поскольку Z(L, p) изменяется с изменением р, не существует ни одного физического направления, независимого от активности и положения сердца. Тем не менее даже в таком обобщенном смысле возможны самое большее три ортогональных отведения. Ниже это положение можно будет естественным образом обобщить, но, по-видимому, проблемы здесь нет.

Другой, в некоторой степени эмпирический подход основан на циклическом характере сердечной активности и, следовательно, графиков потенциалов различных отведений. Различные эксперименты с исключением и совмещением отведений, а также [2] и работы авторов показали, что для здоровых людей функции потенциалов большинства отведений, как идеальных, так и неидеальных, образуют некоторую "трехфункциональную" систему. Это значит, что можно найти три временные функции V₁(t), V₂(t), V₃(t), реализуемые в качестве функций потенциалов отведений, такие, что для каждого отведения L существуют три таких вещественных числа a₁(L), a₂(L) и a₃(L), что будет (приблизительно) справедливо равенство

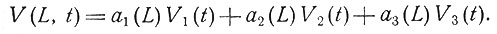
Если V₁, V₂ и V₃ выбраны так, что

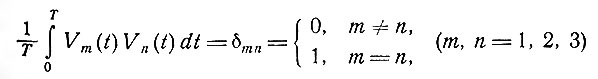
(а это всегда возможно), и если определить

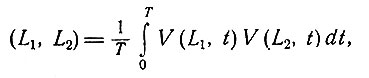
то будем иметь

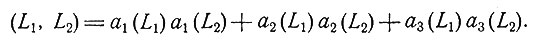
Это определение скалярного произведения отличается от определения, использовавшегося для идеальных отведений; и здесь возникает иное понятие ортогональности. Для идеальных отведений L

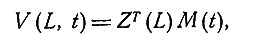
так что для двух идеальных отведений

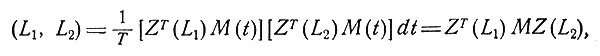
где M - матрица

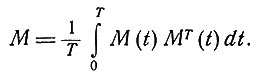
Можно выбрать три новых идеальных отведения L₁, L₂ и L₃ (для начала обеспечив их линейную независимость) таким образом, чтобы они были ортогональны во времени и как идеальные отведения. То есть мы имеем

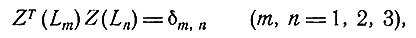
а также

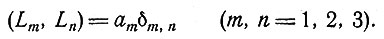
Этого можно достичь, определив собственные значения и собственные векторы указанной выше матрицы М. Основные трудности практической реализации заключаются в измерении Z(L,t) и построении идеальных отведений.

Эквивалентные диполи и псевдодиполи. Идеальные отведения являются особыми в том смысле, что в области сердца векторная функция преобразования импедансов не изменяется. Учет следующего члена (в разложении Тейлора) дает класс отведений первого порядка, т. е. отведений, для которых

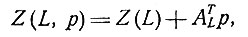
где под р подразумевается вектор, направленный из центра области Н в точку р, a A_L есть (3×3)-матрица.

Если m(р) - плотность дипольных моментов, определенная для р в H, то потенциал отведения выражается формулой

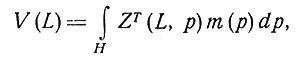
где интеграл берется по объему области Н (тройной интеграл), a dp - объем элемента dxdydz, где p^T = (x, y, z). Тогда потенциал отведения L первого порядка становится равным

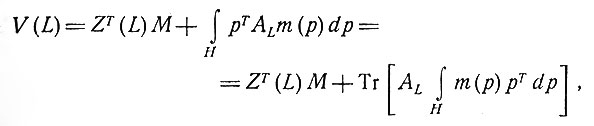
где 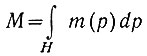- общий дипольный момент. След матрицы, как обычно, есть сумма диагональных элементов.

Надо отметить, что система возможных отведений первого порядка (включая отведения нулевого порядка, или "идеальные") оказывается 12-мерной [3 от Z(L) и 9 от AL]. Если имеется двенадцать линейно независимых отведений первого порядка, то из них можно получить любое другое отведение первого порядка, вне зависимости от характера работы сердца и ее изменения во времени, а также от индивидуальных особенностей обследуемого, хотя коэффициенты в этой комбинации могут зависеть от строения тела и т. д., но не от положения или режима работы сердца. Это число двенадцать, вероятно, случайно соответствует числу стандартных отведений, использующихся в клинической практике.

Обратимся теперь к эквивалентным диполям и псевдодиполям. Мы говорим, что в р* существует эквивалентный диполь М*. если для всех отведений L имеем V(L) = Z^T(L, p*)M*. Поскольку для всех идеальных отведений это должно иметь место, можно видеть, что М* = М, где М - общий дипольный момент сердца. В качестве условия существования эквивалентного диполя для отведения первого порядка требуется, чтобы выполнялось равенство

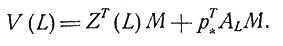
Это выражение должно быть тождественно с

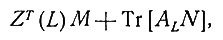
где

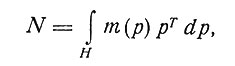
так что эквивалентный диполь существует тогда и только тогда, когда ранг матрицы N равен 1 и она имеет вид

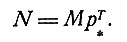
Вообще говоря, требование существования эквивалентного диполя является слишком сильным. В этой связи интересно рассмотреть несколько линейно независимых отведений первого порядка, для которых потенциал отведения

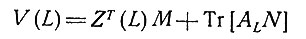
дается также выражением

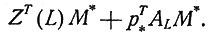
Как было отмечено ранее, равенство этих выражений для идеальных отведений может быть достигнуто, если положить М* = М; кроме того, должно быть

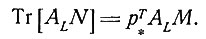
Анализ этого уравнения показывает, что оно может удовлетворяться для трех отведений L₁, L₂ и L₃ с соответствующими матрицами A₁, A₂ и A₃, если векторы q₁ = A₁M, q₂ = A₂M и q₃ = A₃M линейно независимы, так что матрица Q = (q₁, q₂, q₃) имеет обратную. Таким образом, система отведения, для которых существуют псевдодиполи, может состоять из шести отведений: трех идеальных и трех неидеальных.

Надо отметить, что расположение псевдодиполя для некоторой системы отведений зависит от m(p, t) благодаря зависимости от общего диполя M{t) и матрицы

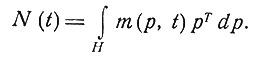
Теперь ясно, что псевдодиполь, вообще говоря, со временем перемещается; эквивалентный диполь, если он существует, в этом случае также перемещается, так как распределение диполей изменяется во времени. Заметим, что эквивалентный диполь является также и псевдодиполем, но не обратно. Условия инвариантности расположения эквивалентного диполя и (или) псевдодиполя не исследовались.

Стоит отметить, что для одного человека существование эквивалентного диполя означает (с явным учетом времени), что

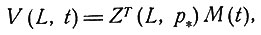
т. е. что система временных функций потенциалов отведений оказывается трехфункциональной системой, в которой основными функциями служат составляющие M₁(t), M₂(t) и M₃(t) вектора М. Поскольку известно, что отведения первого порядка (можно считать, что они достаточно хорошо совпадают с реальными отведениями) образуют 12-функциональную систему, число двенадцать представляет собой максимальное число временных функций линейно независимых потенциалов отведений у одного человека. Неудачи экспериментов с исключением четырех отведений и совмещением трех фиксированных отведений и анализ, выполненный Шером, показали, что даже для здоровых людей существует более трех линейно независимых временных функций. Следовательно, введение понятия эквивалентного диполя справедливо только как некоторая аппроксимация. Что же касается концепции псевдодиполей, то она, конечно, остается в силе независимо от ее полезности.

n-функциональные системы. Разработанный Шером [2] и авторами данной работы подход к использованию электрокардиограммы основан на анализе временных функций разностей потенциалов от нескольких отведений. Шер ограничивал анализ индивидуальных ЭКГ комплексом QRS. Авторы проанализировали ЭКГ от трех отведений, разбив испытуемых на две группы, одна из которых, N, согласно клиническим критериям, состояла из здоровых людей, другая, LVH,- из лиц с гипертрофией левого желудочка. Интересно рассмотреть получающиеся при этом функции и условия того, что они образуют n-функциональную систему.

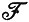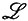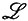Пусть f(L, t) - множество функций , причем 0≤t<T и L∈ где - некоторая система индексов (соответствующая здесь системе отведений, но вообще произвольная); мы говорим, что множество 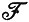образует n-функциональную систему, если существует n таких функций g₁(t), g₂(t), ..., g_n(t), 0≤t<T что для каждого L∈ 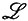можно найти n таких чисел a₁(L), a₂(L),... , a_n(L), зависящих от L, что

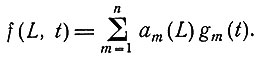
Обычно 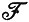рассматривается как n-функциональная система временных функций, но очевидно, что здесь 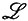и [0, T) равноправны, а функция f(L, t) определена на прямом произведении 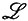×[0, Т) и представляет собой обобщенную матрицу ранга n.

Как уже указывалось, если существует эквивалентный диполь, то система временных функций потенциалов отведений образует трехфункциональную систему.

Практически задача сводится к определению функций g_m(t), их числа и коэффициентов a_m(L). Это делается на основе соответствующей матричной теоремы путем выбора достаточного количества отведений или, в более общем случае, точек в системе индексов и допущения, что ранг матрицы S есть n; элементы матрицы S получаются по формуле

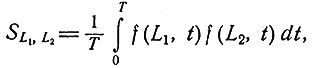
где L₁ и L₂ принимают значения из одного и того же конечного подмножества 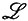_N множества 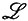. Конечно, размерность N матрицы S должна превышать n, а ранг, который обычно рассматривается,- это ранг некоторого "достаточно хорошего приближения" матрицы S (статистический ранг). Для решения этой проблемы надо заметить, что (N×N)-матрица S является симметричной неотрицательно определенной матрицей. Следовательно,

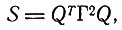
где Q - это (N×N)-матрица, а Г² - неотрицательная диагональная (N×N)-матрица. Теперь можно убедиться, что ранг матрицы S представляет собой число ненулевых элементов матрицы Г² и что "статистический ранг" получается отбрасыванием малых элементов Г как нулевых (из-за "случайных вариаций", связанных с "ошибками" в f(L,t)).

Данное представление матрицы S позволяет нам образовать такую систему функций g₁(t), g₂(t),..., g_n(t) (где n - ранг S), что

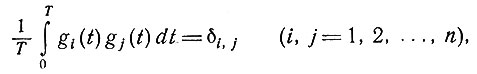
т. е. эти функции образуют ортогональную систему. В частности, если

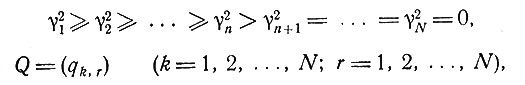
то

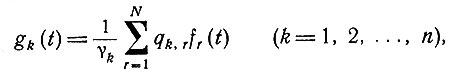
что можно легко проверить. Далее,

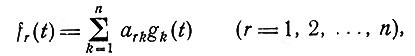
где

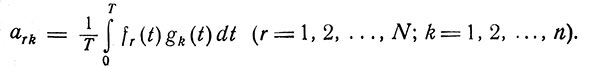
Анализ образов применительно к электрокардиограмме. Можно по-разному анализировать совокупность временных функций потенциалов отведений, например: несколько отведений, взятых одновременно у одного человека, или одно отведение у данного человека для нескольких различных отрезков времени; одну группу отведений у нескольких человек и т. д. В каждом случае можно найти статистический ранг, скажем п, как основу для конструирования я-функциональной системы и для проведения дальнейшего анализа. В этой части статьи берется группа измерений для трех ортогональных отведений в модифицированном варианте системы отведений SVEC-III.

При анализе трех отведений у каждого человека из групп N и LVH приходится иметь дело с большим числом отведений. Начиная отсчет времени с вершины R-зубпа в отведении X и учитывая общий интервал времени для всех лиц, включающих активный период (зубцы Р, QRS и Т), получаем основу для всех ^-функциональных систем. (Практически такой анализ для экономии машинного времени был произведен с помощью коэффициентов Фурье, но представленные здесь результаты преобразованы во временные зависимости.) Каждое из трех отведений имеет восемь составляющих (по восьми базисных функций), так что общую векторную кардиограмму можно восстановить по 24 числам (и таблицам восьми базисных временных функций).

Как указывалось в вводном разделе, мы теперь подошли к тому, что, в частности,

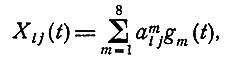
где индекс о соответствует отведению X, Y или Z, индекс i соответствует данному человеку, a t - время. Базисные функции g₁(t), g₂(t), ..., g_n(t) представляют восемь классов образов, а коэффициенты a^m_ij, по 24 для каждого i, характеризуют индивидуальную векторную кардиограмму данного пациента.

Теперь сложная исходная задача анализа формы ЭКГ сводится к геометрии 8-мерного пространства. Имеет смысл сделать несколько замечаний относительно применения этого подхода к решению других задач.

Из трех отведений у одного человека можно образовать трехмерное подпространство общего 8-мерного пространства; таким образом, индивидуальные электрокардиограммы значительно различаются, однако не все люди вносят новое в форму ЭКГ - существует только восемь классов образов.

С другой стороны, 24 числа, которые здесь характеризуют индивидуальную векторную кардиограмму, могут быть использованы в качестве критериев для распознавания. Для различения результатов исследования кардиограмм двух упомянутых групп можно использовать теорему Байеса. В зависимости от распределения этих 24 чисел внутри групп и между группами можно применить нелинейный или линейный анализ полученных результатов или еще более общий метод, требующий рассмотрения отношения плотности двух функций распределения.

Выводы. Понятие образа, до сих пор не определенное во многих областях, свелось к геометрии векторных пространств небольшой размерности и к применению вычислительных методов для разложения вектора на компоненты для данной электрокардиограммы. После того как это выполнено, для эффективного решения таких важных проблем, как классификация образов и постановка предварительного диагноза, могут быть использованы классические статистические методы. Применение этих методов без соответствующей предварительной обработки данных не дает хороших результатов.

В работе освещаются такие проблемы, как установление необходимого количества отведений. Далее охарактеризовано соотношение векторной кардиограммы и ЭКГ от 12 стандартных отведений и показаны возможности использования векторной кардиограммы для обследования отдельных лиц и системы 12 отведений - для целых групп. Иными словами, информацию, представленную совокупностью всех отведений у здоровых людей, можно получить из трех отведений. Могут понадобиться все 12 отведений для того, чтобы определить по кардиограмме информацию о строении тела, положении сердца и о смещении отведений у данного обследуемого, если известна группа, к которой он принадлежит.

Результаты данной работы дают основу для правильного использования методов машинного распознавания образов в электрокардиографии.

Литература

1. Cady L. D., A computer program for measurement of electrocardiogram wave amplitudes, areas and durations, Am. Heart J., 61 (1961), 138.
2. Scher A. M., Young A. C, Meredith W. M., Factor analysis of the electrocardiogram: a test of electrocardiographic theory. Normal hearts, Circulation Research, 8 (1960), 519.
3. Rogers D. J., Tanimoto T. T., A computer program for classifying plants, Science, 132 (1960), 1115.
4. Abildskov J. A., Street W. W., Solomon E., Toomajian A. H., Clinical observations with the frank precordial lead system, Circulation, 17 (1958), 1069.
5. Pipberger H. V., Bialek S. M., Perloff J. K., Schnaper H. W., Correlation of clinical information in the standard 12-lead ECG and in a corrected orthogonal 3-lead ECG, Am. Heart J., 61 (1961), 34.
6. Schmitt O., Lead vectors and transfer impedance, Ann. N. Y. Acad. Set., 65 (6), (1957), 1092-1109.
7. Woodbury M. A., Cady L. D., Tick L. J., Gertler M. M., A computer procedure for screening heart records for normal and enlarged hearts; не опубликовано, представлено в American Society for Clinical Investigation, Atlantic City, April, 1960.