
Медицинская диагностика и современные методы выбора решения. Р. Ледли. Национальный Биомедицинский исследовательский центр, Силвер Спринг. Л. Ластед. Рочестерская Медицинская школа, Рочестер
1. Введение
1.1. Логика в диагнозе. В процессе установления диагноза и выработки рекомендуемого лечения врач часто сталкивается с целой последовательностью сложных решений. В большинстве случаев врач находит решения эвристическим путем, полагаясь на свою интуицию. Для выработки соответствующих навыков ему приходится проходить долгий курс обучения, включающий 10-12-летние занятия в учебных заведениях, практику в больнице и часто еще несколько лет специальной подготовки. К сожалению, за эти годы будущему специалисту лишь изредка, если вообще когда-либо, приходится сталкиваться с логическими основами диагностики или с самими методами выбора решения, хотя и то и другое составляет важную часть его ответственной деятельности. Соответствующими приемами врач постепенно овладевает чисто практически. Из публикаций в медицинских журналах, обширных дискуссий и историй болезней явствует, что вопросы эффективности методов диагностики имеют огромное значение в медицине*. В медицинской литературе находят свое отражение и крайне трудные случаи, в которых врачу часто приходится принимать ответственные решения**. Отсюда с очевидностью вытекает потребность аналитически сформулировать такого рода задачи, с которыми сталкивается врач. Цель этой статьи - отчетливо сформулировать в математических терминах логические основы диагностики и выбора метода лечения***.
* (См., например, Douthwarte A. H., Mistakes in diagnosis, Med. World London, 79 (1953), 113-115; Douthwarte A. H., Pitfalls in medicine, Brit. Med. J., 2 (1956), 895-900, 958-967; Misdiagnoses (editorial), Lancet, 1 (1953), 1034; Clendening L., Hachinger E. H., Methods of diagnosis, St. Louis, Mo., 1947, стр. 73-76. В New Engl. J. Med. еженедельно публикуются клинико-патологические задачи, извлекаемые из архива Массачусетской больницы.)
** (Sperry W. L., The ethical basis of medical practice, New York, 1950.)
*** (См. также Ledley R. S., Lusted L. В., Reasoning foundations of medical diagnosis, Science, 130, № 3366 (1959), 9-21. (Русский перевод: Ледли Р. С, Ластед Л. Б., Объективные основания диагноза, Кибернетический сборник, вып 2, ИЛ, М., 1961.) Ledley R. S., Lusted L. В., The use of electronic, computers to aid in medical diagnosis, Proc. JRE, 47, № 11 (1959) 1970-1977.)
1.2. План статьи. Мы покажем здесь, как с помощью метода последовательного принятия решений, использующего логический анализ для выделения возможных диагнозов, можно найти их вероятности и выбрать метод лечения. В своей практической деятельности врач начинает с того, что применяет итерационный процесс, каждый этап которого состоит из логического анализа и дополнительных исследований, сужающих шаг за шагом круг возможных диагнозов. Если какая-то неопределенность в диагнозе все же остается, то по формуле Байеса можно получить полезные количественные оценки влияния на диагноз соотношений между заболеваниями и симптомами, а также влияния случайных факторов, как-то времени года, наличия эпидемий и т. п. Основная цель установления диагноза - это, безусловно, назначенние соответствующего лечения. Однако мы часто располагаем несколькими возможными методами лечения, и выбор одного из них может происходить в различных условиях: в бесспорной ситуации, в условиях риска, в условиях неопределенности. Во многих случаях, когда точный диагноз не установлен, последовательность циклов "диагноз-лечение" можно выбрать методами динамического программирования. Если пытаться использовать все эти рекомендации на практике, то почти неизбежным окажется применение быстродействующих вычислительных устройств; но даже используя эти машины, нужно следить за тем, чтобы данные перерабатывались ими достаточно быстро. Здесь важно заметить, что корреляционные методы не играют существенной роли в медицинской диагностике, так как установление диагноза - это не таксономическая классификация, и цель его состоит в том, чтобы логическим путем прийти к однозначному указанию заболевания (даже в том случае, когда формулировка окончательного диагноза учитывает и результаты терапии).
Описываемые в статье методы основываются на весьма общем подходе к проблеме; они представляют собой попытку создать основу, на которой можно было бы в дальнейшем разрабатывать отдельные детали и практические применения. Здесь во всей общности рассматривается логическая сторона задач диагностики и область приложения новых методов, а обзор других проблем дает возможность охватить перспективы этой теории. Такой подход позволит в дальнейшем дать точное математическое описание отдельных частных случаев и выявить скрытые предположения, используемые в некоторых других приемах диагностики. В этой статье мы бегло касаемся многих проблем и подходов к их решению.
1.3. Подход к задачам и ограничения. Наша цель состоит в применении уже разработанных математических методов к задачам медицинской диагностики. Мы не будем предлагать новых математических методов, а вместо этого постараемся ставить задачи, которые можно решить уже известными методами.
В нашей статье, однако, не рассматривается ряд условий, необходимых для практического применения описанных методов. Во-первых, ясно, что данные, не попавшие на "вход", влияния на "выход" не окажут, а неверные данные, пробелы в истории болезни, ошибки в лабораторных исследованиях, неправильное истолкование результатов исследования,- все это должно сказаться на результатах, выданных вычислительной машиной. Это замечание относится, впрочем, ко всякому методу установления диагноза и выбора лечения. Во-вторых, использование вычислительных машин потребует стандартизации медицинской номенклатуры, ибо машина может отождествить одинаковые вещи, по-разному названные, но она, очевидно, не сможет вложить различный смысл в один и тот же термин. В-третьих, остается извечная проблема единообразного истолкования результатов исследований. Например, какое содержание сахара в крови свидетельствует о наличии диабета? Стандартное истолкование должно свести к минимуму возможность ошибок, но следует помнить, что полностью исключить ошибки невозможно. Наконец, чрезвычайно важно, чтобы врач был в курсе новейших достижений в области диагностики, терапии и мер, предупреждающих заболевания. Некоторые врачи считают, что неизбежное опоздание, с которым внедряются новые методы, обеспечивает возможность более тщательного ознакомления с этими методами, но это отражает лишь несовершенство путей, по которым достижения науки доходят до врача-практика. Все перечисленные проблемы также можно решать математическими методами, но эти проблемы часто оказываются слишком трудными и требуют особого рассмотрения.
Предлагаемый здесь математический аппарат должен оказать помощь врачу, например, в отделении логических основ диагностики от побочных соображений, основанных на факторах, трудно поддающихся учету, и в установлении некоторых количественных оценок. Такое отделение даст возможность врачу точнее определить трудно уловимые факторы и тем самым сосредоточить внимание на наиболее сложных вопросах. Кроме того, поскольку логические процессы допускают точный анализ, появление ошибок с этой стороны можно исключить.
Использование вычислительных устройств ни в коей мере не означает передачу этим устройствам функций врача. Наоборот, роль врача становится при этом еще более трудной. Врачу придется быть более образованным: помимо своих профессиональных знаний, которыми он пользуется в настоящее время, ему придется овладеть и теми новыми методами, о которых говорится в этой статье. Однако мы надеемся, что ценой дополнительных усилий можно будет добиться выигрыша в точности диагноза и эффективности лечения.
2. Логика в диагностике
2.1. Роль логики. Логические элементы в задаче установления диагноза имеют следующие источники: 1) медицинские знания, 2) симптомы, обнаруживаемые у больного, и 3) сам окончательный диагноз. Медицинские знания содержат некоторую информацию о соотношениях между симптомами и болезнями. Симптомы* дают дальнейшую информацию о самом больном. Исходя из этих двух источников информации, методами исчисления предложений ставится диагноз. Пусть n - число симптомов, а m - число болезней. Обозначим симптомы
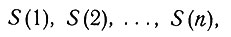
а болезни -
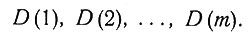
* (В этой статье термины симптом, признак, результат исследования считаются синонимами. Они охватывают данные истории болезни, лабораторных анализов и т. п. В каждом конкретном случае врач решает, обнаруживается или нет определенный симптом.)
По отношению к определенному больному символ S(i) будет означать, что этот больной обнаруживает i-й симптом, а символ D(j) - что больной страдает j-м из перечисленных заболеваний. В табл. 1 дана сводка обозначений, употребляемых здесь для отрицания, (логических) произведений и суммы, а также для импликации. Представим себе всевозможные комбинации перечисленных симптомов и заболеваний, которые могут быть обнаружены у данного пациента; общее число таких комбинаций равно 2n+m. Например, столбцы рис. 1 образуют такой перечень для случая трех симптомов и трех заболеваний; при этом единица означает, что соответствующий симптом обнаруживается или соответствующее заболевание имеет место, а нуль означает, что такого симптома или заболевания нет. Так, столбец, отмеченный стрелкой, содержит следующие данные: у больного наблюдаются симптомы S(1) и S(2) и не наблюдается S(3); в то же время он страдает заболеванием D(2), тогда как D(1) и D(3) у него нет. Любую такую комбинацию мы условимся называть комплексом симптомов и заболеваний (в дальнейшем кратко КС3) и обозначать Сij; произвольную комбинацию симптомов будем называть комплексом симптомов (кратко КС) и обозначать si, а комбинацию заболеваний - комплексом заболеваний (кратко КЗ) dj. В этих обозначениях
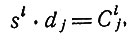
а рис. 1 можно рассматривать как иллюстрацию этого соотношения.
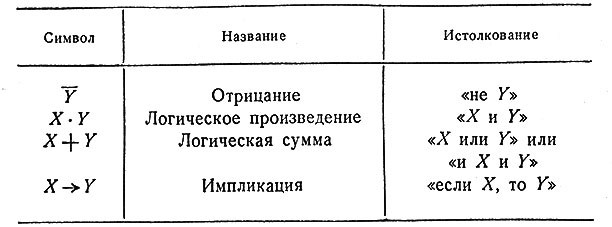
Таблица 1. Сводка обозначений
Матрицу из нулей и единиц, пример которой приведен на рис. 1, назовем логическим базисом данных симптомов и заболеваний. Столбцы этой матрицы изображают все мыслимые КСЗ.

Рис. 1. Логический базис к примеру в тексте (указаны комплексы симптомов и заболеваний; число их сокращено на основании данных медицины)
Мы употребили слово "мыслимые", а не "возможные", так как не все они могут иметь место в действительности. Указать, какие КСЗ могут иметь место, а какие нет,- дело медицины. Предположим, что в нашем примере медицина дает нам следующие указания:


1 (Мы понимаем, конечно, что наличие симптома может свидетельствовать о наличии заболевания, но отсутствие явных симптомов вовсе не означает отсутствия заболевания.)
Логическое произведение этих предложений является булевской функцией
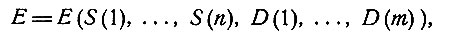
выражающей соотношения между заболеваниями и симптомами, почерпнутые из медицинской науки. В нашем примере
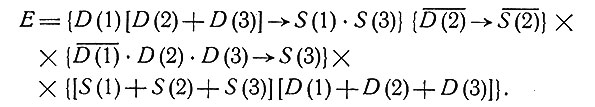
Столбцы, вычеркнутые на рис. 1, представляют собой КСЗ, для каждого из которых ложно хотя бы одно из предложений, входящих в E в качестве сомножителей. Рассмотрим, например, столбец С67, самый правый из вычеркнутых:

Этот КСЗ относится к пациенту, страдающему всеми тремя заболеваниями D(1), D(2), D(3), но не обнаруживающему симптома S(1). Такая картина противоречит утверждению 1, поэтому указанный столбец вычеркивается. Другими словами, после вычеркивания остаются столбцы, содержание которых согласуется с данными медицины. Оставшиеся столбцы в совокупности образуют так называемый приведенный логический базис.
Пусть теперь перед нами конкретный больной, и мы должны поставить диагноз. Какие-то симптомы у него обнаружены, какие-то другие - нет; в общем случае есть еще и третья группа симптомов, относительно которых в данный момент мы не располагаем сведениями. Такая совокупность симптомов, быть может неполная, называется профилем симптомов больного и обозначается G. Одновременно рассматривается совокупность заболеваний (быть может, неполная) - профиль заболеваний f. Оба профиля вместе образуют профиль симптомов и заболеваний f*G. Профиль G есть булевская функция симптомов
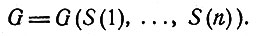
Теперь мы можем сформулировать логическую задачу: по заданным профилю симптомов G и функции Е найти профиль заболеваний f как булевскую функцию аргументов D(1),..., D(m):
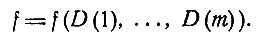
Предположим в нашем примере, что у пациента наблюдается симптом S(2) и не наблюдается симптома S(1), т. е.
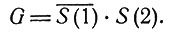
В приведенном логическом базисе этому условию удовлетворяют КСЗ в столбцах С22, C62 и C66 которые соответствуют комплексам заболеваний d2 и d6. Итак, мы приходим к диагнозу
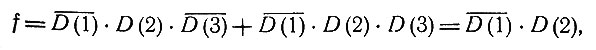
т. е. у пациента есть заболевание D(2), нет D(1), а относительно D(3) мы ничего сказать не можем.
2.2. Формулировка в терминах булевских алгебр. Теперь мы в состоянии сформулировать в абстрактном виде логическую задачу медицинской диагностики. Сначала мы рассмотрим свободную булевскую алгебру В, образующими которой служат элементы
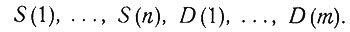
Булевскую функцию Е, содержащую данные медицинской науки, мы будем рассматривать как ограничение, с помощью которого строится несвободная булевская факторалгебра
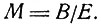
Построение это осуществляется следующим образом. Пусть Н - гомоморфизм алгебры В в себя, т. е. такое отображение алгебры B в B, что для любых Xr, Xs∈B выполнены равенства
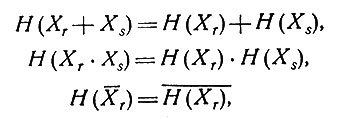
причем H(E) = I, где I - "всегда истинный" элемент (такой, что Xr*I = Xr для любого Xr∈B). Пусть {Е} - ядро этого гомоморфизма. Булевская алгебра М = В/Е есть, по определению, совокупность классов {X}i, устроенных таким образом, что вместе с произвольно выбранным Xr в класс {X}i входят все те Xs, для которых H(XS) = H(Xr). Операции в М определяются равенствами
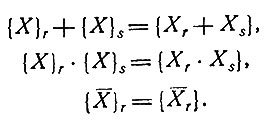
В М автоматически выполняется соотношение, которое в В было обозначено Е.
Существует довольно простой вычислительный метод, использующий представление элементов булевской алгебры В в виде векторов с компонентами, принимающими значения лишь 0 и 1*. (В нашем примере образующими свободной булевской алгебры служат столбцы на рис. 1.) С помощью логических операций сложения, умножения и обращения можно найти любой элемент булевской алгебры. Операции эти таковы: 1 + 0 = 0 + 1 = 1 + 1 = 1, 0 + 0 = 0, 1*0 = 0*1 = 0*0 = 0, 1*1 = 1, 1- = 0, 0- = 1; P→Q эквивалентно P-+Q. Например,

* (См. Ledley R. S., Digital computer and control engineering, New York, 1960, гл. 11-14.)
Если пользоваться лишь векторами приведенного базиса, то можно получить аналогичное представление булевской факторалгебры. Приведенный базис состоит из векторов, оставшихся после вычеркивания тех столбцов матрицы, которые соответствуют нулям в векторном представлении функции Е. В нашем примере Е есть произведение (в указанном выше смысле) только что перечисленных четырех векторов, т. е.
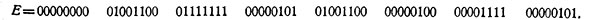
На рис. 1 вычеркнуты как раз те столбцы, которые соответствуют нулям этого вектора. Приведенный базис, образованный оставшимися столбцами, согласуется сданными медицины.
Теперь мы можем сформулировать основную формулу медицинской диагностики:
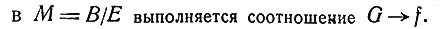
Здесь М - описанная выше булевская факторалгебра, G - совокупность симптомов, обнаруженных у больного, f - искомый диагноз. Логическая задача медицинской диагностики состоит в том, что по заданному G ищется такое f, чтобы в факторалгебре М имела место импликация G→f.
Эту основную задачу можно решить с помощью различных алгоритмов; мы упомянем три из них. Первый - алгоритм полного поиска - по существу тождествен с элементарным способом, разобранным выше. Полный поиск состоит в том, что просматриваются столбцы, образующие приведенный базис, и отмечаются те из них, КС которых согласуется с G, профилем симптомов больного. Искомый диагноз f получится, если взять логическую сумму комплексов заболеваний в отмеченных столбцах.
Пусть, например,
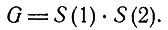
Такому G соответствуют четыре возможных КЗ, а именно d2, d3, d6 и d7, и мы приходим к диагнозу
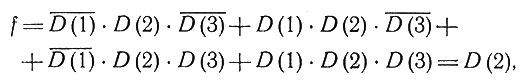
согласно которому пациент страдает заболеванием D(2), а D(1) и D(3) мы пока ничего не можем сказать. Пусть теперь
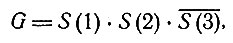
т. е. при первом исследовании мы ничего не знали о симптоме S(3), а при дополнительном исследовании мы его у больного не обнаружили. В результате получаем однозначный диагноз
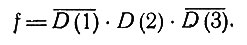
Второй алгоритм, требующий построения ветвящейся схемы, подобен методу последовательных поисков. На рис. 2 показана ветвящаяся схема, относящаяся к рис. 1.
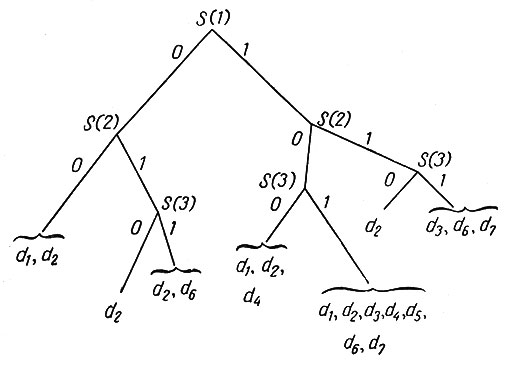
Рис. 2. Ветвящаяся схема (к примеру на рис. 1)
Заметим, что, применяя этот метод, мы должны рассматривать симптомы в том порядке, в каком они появляются на схеме, а на практике это не всегда осуществимо. Третий метод, использующий уравнения с булевскими матрицами, подробно изложен в гл. 13 книги, указанной в сноске на стр. 151*.
* (См. также Ledley R. S., Digital computational methods in symbolic logic with examples in biochemistry, Proc. Nat. Acad. Set USA, 41, № 7 (1955), 498-511.)
2.3. Минимальное воспроизведение алгебры М. Все эти методы было бы желательно применять практически в различных областях медицины. Интересно отметить, что такие области очень редко охватывают более 300 болезней и, скажем, 200 характерных симптомов (даже врач-терапевт или хирург в своей практике обычно имеет дело с весьма ограниченным числом болезней, предпочитая в остальных случаях направлять больных к другим специалистам). Но уже при 500 образующих потребуется память объемом 500×2500≈500×10150 бит! Конечно, нам нужна только булевская факторалгебра М = В/Е, а не сама В. Учебник по какой-либо отрасли медицины должен фактически воспроизводить М в некоторой символической записи (поскольку слова представляют собой символы идей), так как в нем должны содержаться данные о связях между симптомами и заболеваниями. Текст, занимающий 400 страниц, содержит около 1 200 000 букв (считая в каждой странице по 40 строк из 75 знаков), для фиксации которых нужно примерно 7 200 000 двоичных знаков (если считать по 6 двоичных знаков на каждую букву). Если предположить, что применение соответствующей логической символики дает 10-кратную экономию в знаках, то нам понадобится 720 000 двоичных знаков, что вполне достижимо в современных устройствах с памятью на магнитных барабанах.
Для вычислений, описанных в предыдущем пункте, представление М формулами математической логики не является наилучшим. В запоминающее устройство на магнитном барабане на 10 000 000 бит можно ввести 20 000 столбцов, каждый на 500 бит; таким образом, если ядро алгебры М (т. е. приведенный базис) содержит не более 20 000 столбцов, то оно может быть непосредственно введено в запоминающее устройство. С другой стороны, если допустить, что 300 болезней, которые мы рассматриваем, входят лишь в 1000 различных комплексов заболеваний и что для записи каждого dj достаточно 20 бит, то на комплексы симптомов остается 9 980 000 бит, по 200 бит на каждый si; при этом мы можем располагать 49 900 комплексами симптомов, т. е. по 50 si на каждый dj.
Однако задача воспроизведения алгебры М допускает дальнейшее упрощение, в основе которого лежит важное понятие минимального множества первичных импликантов булевской функции Е. Произведение Р' некоторого числа образующих называется импликантом булевской функции Е, если Р' → Е; если не существует такого Р≠Р' что Р'→Р и Р→E, то Р' называется первичным импликантом. Это понятие используется при построении так называемой простейшей дизъюнктивной формы булевской функции Е. Рассмотрим, например, вектор
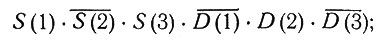
среди его компонент есть только одна 1, и она соответствует столбцу С25. Просуммируем все такие произведения, у которых единица не может появиться на том месте, где у Е стоит нуль. Тогда Е запишется в дизъюнктивной форме, т. е. в виде суммы произведений. Однако среди этих произведений может встретиться следующее:
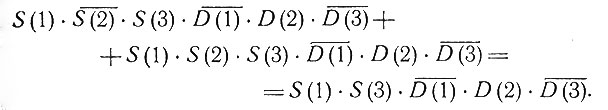
Правая часть равенства не только состоит из меньшего числа образующих, но его векторное представление содержит две компоненты, равные 1. Им соответствуют два столбца

где на месте двойки может стоять и нуль и единица. Аналогично четыре столбца

что соответствует произведению
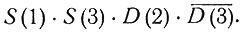
Чем дальше проводить такое приведение столбцов, тем меньше образующих войдет в соответствующие произведения; эти последние будут следствиями исходных произведений, и в то же время они будут служить импликантами булевской функции Е. Процесс можно продолжать до тех пор, пока получаемый импликант не окажется первичным*. Если мы образуем всевозможные первичные импликанты булевской функции Е, то, взяв их сумму, получим для Е простейшую дизъюнктивную форму**. Одновременно мы находим наименьшее число столбцов, содержащих 0, 1 и 2, которые представляют Е, и таким образом строим ядро алгебры М. Приведем здесь столбцы, отвечающие примеру, показанному на рис. 1:

* (Заметим, что X→Y тогда и только тогда, когда любой компоненте векторного представления X, равной 1, соответствует компонента Y, также равная 1.)
** (См. стр. 331-343 и 365 книги, указанной в сноске на стр. 151.)
Мы получили 9 столбцов вместо 22. При большем числе образующих относительное сокращение оказывается еще более значительным. Если столбцы, образующие базис, рассматривать как вершины (m + n)-мерного куба, то описанный процесс можно истолковать как процесс отыскания куба меньшего числа измерений, все вершины которого представляют собой столбцы, соответствующие единицам в векторном представлении функции Е. Именно в силу значительного уменьшения количества столбцов желательно записывать приведенный базис алгебры М в такой форме.
3. Задача последовательного уточнения диагноза
3.1. Пример, иллюстрирующий задачу. Проведение различных анализов или обнаружение различных симптомов может быть как очень простым, так и весьма затруднительным из-за различий в сложности необходимого оборудования, в цене препаратов, из-за неудобств, причиняемых больному, и т. д. В любой конкретной области медицины возможные симптомы можно классифицировать по степени трудности их обнаружения. Так, например, часто бывает совсем просто получить некоторые сведения из истории болезни; одни этапы непосредственного обследования самого больного проще других; анализы крови и рентгенографические исследования также различны по своей сложности и стоимости; наконец, к некоторым исследованиям, таким, как, например, биопсия или пробные операции, следует прибегать лишь тогда, когда необходимую информацию нельзя получить иными способами. Ясно, что для установления диагноза нет надобности проводить все возможные исследования. Более реален такой метод, при котором сначала проводится некоторая совокупность исследований, выясняется, можно ли на основе полученных данных поставить точный диагноз и, если нельзя, какие дополнительные исследования нужны, потом проводятся эти дополнительные исследования и т. д. (см. рис. 3).
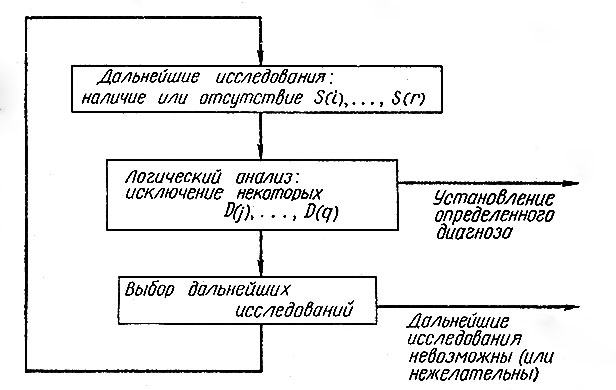
Рис. 3. Итерации процесса 'диагноз - лечение'
Покажем на примере, каким образом эту задачу можно сформулировать в терминах математической логики. На рис. 4 отмечены комплексы симптомов и заболеваний, соответствующие 14 симптомам и 8 заболеваниям. В этом примере симптомы разделены на следующие группы: данные истории болезни, данные физического осмотра, результаты анализов крови и результаты анализов костного мозга; они расположены в порядке увеличения сложности исследования. Заметим, что S(1) ничего не дает для диагноза: во всех столбцах верхняя цифра есть 1. Предположим, что у какого-то больного обнаружены, помимо S(1), также симптомы S(2) и S(3). На этом этапе исследования можно сделать заключение, что искомый комплекс заболеваний пациента заключен в первых 11 столбцах; остальные столбцы (затененные на рис. 4) можно исключить из рассмотрения. Переходя ко второй группе симптомов (данных непосредственного осмотра), замечаем, что, поскольку мы рассматриваем лишь первые 11 столбцов, все три исследования S(4), S(5) и S(6) не нужны, достаточно любых двух из них. Возьмем S(4) и S(5) и предположим, что у больного обнаружен симптом S(4) и не обнаружен S(5). При этом возможными оказываются только 7 столбцов, с 3-го по 9-й (см. рис. 4). Значительно труднее указать, какие следует проделать анализы крови S(7), ..., S(12). Ниже будет показано, что необходимы лишь S(9), S(10) и S(12). Допустим, что на S(9) и S(12) получена положительная реакция, а на S(10) - отрицательная. Тогда, как указано на рис. 4, остается только 5-й столбец. Надобность в исследованиях костного мозга отпадает. Больной страдает некоторой комбинацией заболеваний D(4) и ?>(5) и никакими другими из фигурирующих в этой таблице. Если же предположить, что в результате физического осмотра у больного обнаружены оба симптома 5(4) и 5(5), то отпадут все столбцы, кроме двух первых; в этом случае анализы крови не нужны, но придется прибегнуть к анализу 5(13) костного мозга.
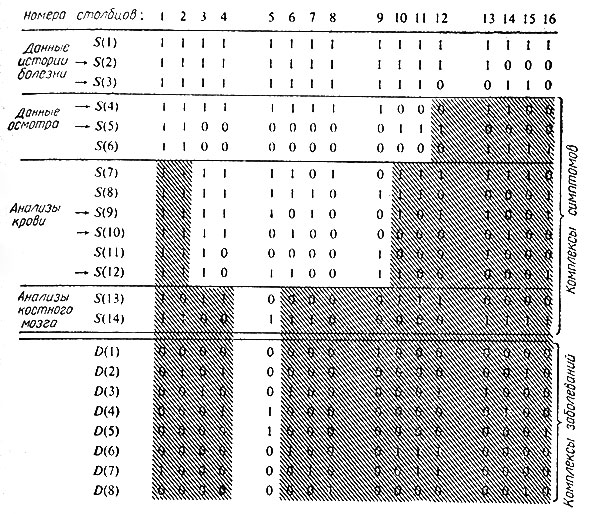
Рис. 4. Логический базис для комплексов симптомов и заболеваний (случай 14 симптомов и 8 заболеваний). После очередной серии исследований рассматриваются возможные диагнозы и решается вопрос о дальнейших исследованиях
Возникает задача об определении на каждой стадии наименьшего количества исследований. Очевидны практические выводы такой минимизации: во-первых, из-за того, что врачи обычно мало заботятся или вовсе не думают о том, чтобы отказаться от ненужных для пациента исследований, госпитальные и клинические лаборатории оказываются перегруженными; во-вторых, сведение ля абораторных исследований к минимуму избавляет пациента от лишних расходов. Кроме того, в отношении исследований, связанных с операциями или с другими рискованными мерами, можно было бы установить, насколько они необходимы. Но надо иметь в виду, что исключение избыточных исследований приводит к тому, что случайная ошибка в результатах проведенных анализов может совершенно исказить диагноз. Поэтому некоторые избыточные исследования могут быть полезны в качестве контрольных.
3.2. Отыскание минимальной серии исследований на каждом этапе. Отыскание на каждой стадии наименьшего числа исследований основывается на следующем замечании: для того чтобы некоторая серия испытаний была эффективной, нужно, чтобы при помощи этих испытаний можно было выделить любой из столбцов, рассматриваемых на данной стадии. Это означает, что для каждого такого столбца существует произведение испытаний из данной серии, векторное представление которого имеет единственную единицу именно в этом столбце. Мы покажем два приема, с помощью которых можно находить такого рода эффективные серии исследований, если только последние вообще существуют. Первый из этих двух приемов требует составления для каждой пары столбцов их "разности", т. е. столбца, содержащего О на тех местах, где исходные столбцы содержат одинаковые цифры, и 1 на тех местах, где в одном из исходных столбцов 0, а в другом 1. Так, например, столбцы

Составим разности незаштрихованных столбцов на рис. 4:

1 (Первые шесть столбцов представляют собой разности 1-го и 2-го, 1-го и 3-го, ..., 1-го и 7-го столбцов, стоящих слева, следующие пять - разности 2-го и 3-го, .... 2-го и 7-го, следующие четыре - разности 3-го и 4-го, 3-го и 7-го и т. д.- Прим. ред.)
Если некоторое исследование S(i) различает какую-либо пару столбцов, то в разности этих столбцов против S(i) будет стоять 1. Следовательно, произведение исследований, не содержащее ни одного из тех S(i), против которых в некоторой разности двух столбцов стоят 1, не будет различать эту пару столбцов. Например, произведение S(7)-S(8)-S(9)-S(10) не содержит обоих исследований, которым соответствуют две единицы в разности 1-го и 2-го столбцов; поэтому в векторном представлении этого произведения компоненты, попадающие в эти столбцы, будут равны 1. Роль разностей столбцов становится ясной. Мы ищем наименьшую серию исследований, обладающую следующим свойством: какова бы ни была пара рассматриваемых столбцов, исследования S(i), соответствующие единицам разности этих столбцов, не должны все оказаться вне искомой серии. Некоторые разности могут быть лишними, а именно те, для которых найдется хотя бы одна другая разность с меньшим числом единиц, но на тех местах, где у последней стоят единицы, у лишней разности тоже должны быть единицы. Тогда эти лишние разности можно вообще изъять. В нашем примере лишние разности отмечены снизу звездочкой. Из этой таблицы видно, что наименьшее количество исследований для всех семи столбцов равно трем. Пробуя различные сочетания из трех S(i), мы обнаруживаем, что лишь тройка S(9), S(10), S(12) удовлетворяет высказанному выше условию; следовав тельно, восемь произведений из этих трех исследований могут дать подходящие векторы. Итак, S(9), S(10) и S(12) образуют минимальную серию необходимых испытаний.
Если один и тот же комплекс заболеваний соответствует нескольким столбцам, изображающим различные комплексы симптомов, то эти столбцы не должны различаться. Поэтому разности таких столбцов не нужны.

Рис. 5. Оставшиеся столбцы, относящиеся к анализам крови (см. рис. 4)
Второй прием, к описанию которого мы переходим, последовательно определяет испытания, разделяющие столбцы на две, по возможности равные, группы. Обращаясь к нашему примеру, прежде всего подсчитаем число единиц в каждой строке, соответствующей симптомам S(7), ..., S(12) на рис. 4 (см. рис. 5). После этого мы выбираем испытание, которое делит столбцы на две примерно равные части; в нашем примере должно быть 3 или 4 единицы в строке, т. е. можно выбрать S(9). Далее мы рассматриваем столбцы, содержащие 1 в строке S(9), и выбираем испытание, делящее их пополам. То же проделываем со столбцами, содержащими 0 в строке S(9); если подойдет то же испытание, что и для единиц, то это еще лучше. Описанный процесс повторяем для выбранного испытания. На рис. 6 иллюстрируется (на том же примере) выбор минимальной серии S(9), S(10) и S(12).
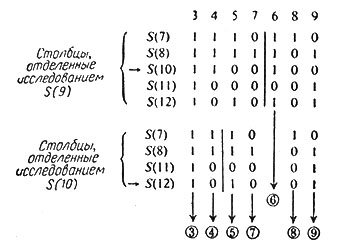
Рис. 6. Отыскание наименьшего числа необходимых исследований
В том случае, когда целью исследования является выяснение того, страдает или нет пациент определенным комплексом заболеваний, найденная таким способом серия испытаний может оказаться не минимальной. Допустим, мы хотим знать, имеет ли место комплекс заболеваний, указанный в 9-м столбце, т. е. заболевание D(1) при отсутствии D(2), ..., D(8). При этом можно рекомендовать такой способ отыскания серии испытаний, "близкой" к минимальной. Перепишем часть таблицы на рис. 4 так, чтобы в 9-м столбце стояли только единицы; для этой цели мы заменим те симптомы S(i), которым отвечают в 9-м столбце нули, их отрицаниями (см. рис. 7).

Рис. 7. Отыскание наименьшего числа исследований, необходимых для выделения 9-го комплекса симптомов и заболеваний
Отметим количество единиц (по строкам), стоящих в столбцах с наименьшим числом нулей*. В примере на рис. 7 наименьшее число нулей, равное 3, содержат столбцы 3-й, 5-й, 6-й и 7-й; в строке 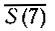 на пересечениях с отмеченными столбцами оказывается единствен-* ная единица, в строке S(8) - четыре единицы, и т. д. Берем сначала испытание, которому в указанном смысле соответствует наименьшее количество единиц. В нашем примере мы можем выбирать между
на пересечениях с отмеченными столбцами оказывается единствен-* ная единица, в строке S(8) - четыре единицы, и т. д. Берем сначала испытание, которому в указанном смысле соответствует наименьшее количество единиц. В нашем примере мы можем выбирать между 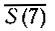 ,
, 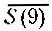 и S(11). Взяв
и S(11). Взяв 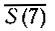 , вычеркнем соответствующую (первую) строку и столбцы, которые на пересечении с этой строкой содержат нули. Затем повторяем эту процедуру с оставшейся таблицей. Ясно, что на втором этапе в нашем примере (см. 7-й столбец на рис. 7) мы можем выбрать любое из испытаний
, вычеркнем соответствующую (первую) строку и столбцы, которые на пересечении с этой строкой содержат нули. Затем повторяем эту процедуру с оставшейся таблицей. Ясно, что на втором этапе в нашем примере (см. 7-й столбец на рис. 7) мы можем выбрать любое из испытаний 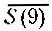 , S(11) или S(12). Таким образом, для того чтобы обнаружить у пациента комплекс заболеваний
, S(11) или S(12). Таким образом, для того чтобы обнаружить у пациента комплекс заболеваний 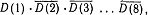 достаточно проделать два испытания.
достаточно проделать два испытания.
* (Столбец 9-й, вовсе не содержащий нулей, при этом не учитывается.- Прим. ред.)
4. Вероятности в диагностике
4.1. Роль вероятностей. Продолжение испытаний с целью уточнения диагноза часто бывает невыполнимо или нежелательно. В таких условиях возникает следующий вопрос: какова вероятность данного комплекса заболеваний при имеющемся у больного профиле симптомов? Вероятность может проникнуть в диагноз прежде всего потому, что она содержится в данных медицины. Действительно, в учебниках медицины мы можем прочитать: "При заболевании dj у больного может обнаружиться симптом si". В настоящее время можно утверждать, что числовые значения вероятностей бывают известны редко; в медицинских справочниках они редко фигурируют. Однако ниже мы покажем, что получить такого рода статистические данные можно сравнительно легко. Так как наше изложение носит достаточно отвлеченный характер, предположим, что мы уже располагаем нужными нам данными о вероятностях или по крайней мере что эти данные доступны. Покажем, как их можно использовать для установления диагноза. Во многих случаях будет ясно указано, какие именно статистические данные понадобятся и как их представить в наиболее полезном виде.
Рассмотрим, например, больного с профилем симптомов 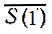 *S(2) (см. рис. 2). Эта комбинация логически указывает два различных заболевания: d2 и d6. Обозначив
*S(2) (см. рис. 2). Эта комбинация логически указывает два различных заболевания: d2 и d6. Обозначив
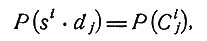
мы получим следующие значения условных вероятностей:
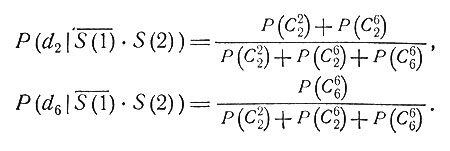
Итак, основная теоретико-вероятностная задача медицинской диагностики состоит в отыскании условных вероятностей
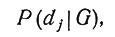
где G - профиль симптомов, обнаруженных у больного, а значения j∈f соответствуют комплексам заболеваний, выявленным логическими методами и методами последовательных испытаний. Эти вероятности, очевидно, зависят от характеристик рассматриваемой группы больных и от количества подлежащих рассмотрению заболеваний. Выберем из исходной совокупности заболеваний D некоторую ее часть D' и обозначим через di' некоторый определенный комплекс заболеваний из D' в сочетании со всевозможными другими заболеваниями из D. Тогда при заданном контингенте больных вероятность P(di'|G) не зависит от количества заболеваний, входящих в D; при этом комплекс заболеваний di', разумеется, интерпретируется так, что те заболевания, входящие в di', которые принадлежат D, но не принадлежат D', могут иметь или не иметь места.
Следует, наконец, заметить, что вероятности, получающиеся на различных стадиях установления диагноза, ни в каком смысле не "стремятся" к какому-либо окончательному значению. Пусть, например, больной страдает определенным заболеванием, которое можно обнаружить специальным анализом. Пока этот анализ не сделан, вероятность заболевания может становиться все меньше и меньше на каждой новой стадии исследования, а когда этот анализ будет сделан, эта вероятность примет значение, равное единице! Тем не менее, когда по той или иной причине врач не прибегает к дополнительным исследованиям, существенную роль в выборе лечения должны играть теоретико-вероятностные соображения.
4.2. Роль формулы Байеса. Формула Байеса позволяет глубоко проникнуть в теоретико-вероятностную сторону диагностики. Пусть заданы комплекс заболеваний dj и комплекс симптомов si; формула Байеса устанавливает связь между условными вероятностями P(dj|si) и P(si|dj), а именно
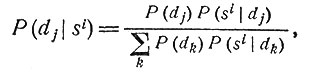
где в знаменателе суммирование распространяется на всевозможные комплексы заболеваний. Роль знаменателя сводится к нормировке, поэтому мы сосредоточим свое внимание на числителе
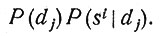
Множитель P(si|dj) есть вероятность того, что при заданном комплексе заболеваний dj больной обнаружит комплекс симптомов si. Оценки таких вероятностей содержатся в учебниках медицины, когда речь идет об определенных болезнях; правда, в настоящее время учебники не дают указаний относительно числовых значений P(si|dj), но они содержат утверждения вроде следующих: при данном заболевании одни симптомы обычны, другие часты, третьи обнаруживаются редко и т. д. О вероятностях P(si|dj) речь идет чаще, чем о P(dj|si), потому что симптомы связаны с болезнями и являются производными от них. Вероятность P(si|dj) обнаружить симптомы si в предположении, что больной страдает заболеваниями dj, есть в общем случае постоянная, зависящая от данного комплекса заболеваний и почти не меняющаяся с изменением других факторов.
Далее, множитель P(dj) есть вероятность того, что больной, выбранный наугад из определенной группы, страдает комплексом заболеваний dj. "Определенной группой" может быть группа всех больных, обслуживаемых определенным врачом, или всех больных, лечащихся в определенной клинике, и т. д. Вероятность P(dj), конечно, существенно зависит от выбора группы больных. В этом множителе сказывается влияние географических, эпидемиологических и социальных факторов, времени года и т. п. Так, тропические заболевания наиболее распространены в тропиках; в период эпидемии азиатского гриппа простудные явления скорее всего могут быть вызваны азиатским гриппом; некоторые заболевания (например, полиомиелит) сильно связаны с сезонными изменениями и т. д. Ясно, что обе эти группы факторов влияют на диагноз. Знать значение знаменателя в формуле Байеса
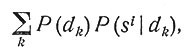
который связан лишь с нормировкой, редко требуется, так как, выбирая наиболее правдоподобный диагноз из нескольких возможных, мы оцениваем не сами вероятности, а их отношения.
Итак, мы можем составить таблицу значений P(si|dj) - постоянных, зависящих лишь от патолого-этиологических особенностей заболевания dj. Далее, для определенной группы больных, например больных, находящихся на излечении в определенной клинике или в ведении определенного врача, выясняются значения вероятностей P(dj), которые определяются внешними условиями. После этого формула Байеса позволяет вычислить вероятности диагнозов P(dj|si). Приблизительно то же, хотя бы с качественной стороны, делает врач, когда говорит своему пациенту по телефону: "Ваше самочувствие - головная боль, озноб, кашель, общее недомогание - указывает, по-видимому, на азиатский грипп; сейчас много случаев гриппа, сами знаете - эпидемия".
Выше было замечено, что нам в сущности важно иметь вероятности P(dj|G), где G - профиль симптомов больного, т. е. некоторая булевская функция симптомов S(i). Легко видеть, что в этом случае формулу Байеса можно записать в виде
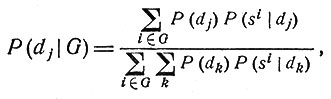
где внешнее суммирование (по i∈G) распространяется по всем комплексам симптомов si входящим в G, т. е. по всем тем комплексам, которым соответствуют столбцы, имеющие единицы в пересечении с вектором G. Аналогичная формула для P(f|G), где профиль заболеваний f представляет собой некоторую булевскую функцию заболеваний, имеет вид
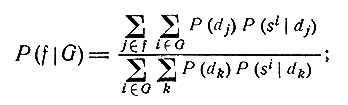
внешнее суммирование в числителе (по j∈f) распространяется по всем комплексам заболеваний, которым соответствуют столбцы, имеющие единицы в пересечении с вектором f.
4.3. Использование формулы Байеса для получения статистических данных. Используя теоретико-вероятностные методы, мы допускаем некоторую натяжку, относящуюся, впрочем, к самой статистике, а не к основам диагностики. Дело в том, что вероятности P(dj) и P(si|dj) относятся к больному, выбранному случайно из некоторой известной группы, а мы применяем их к новому больному (не принадлежащему к этой группе), обратившемуся за помощью к врачу. Мы не будем детально обсуждать вопрос, почему такое применение этих вероятностей оправдывает себя; подобная ситуация встречается в самых разнообразных областях человеческой практики. Но некоторые общие статистические соображения помогут нам уяснить отдельные детали теоретико-вероятностного подхода к задачам медицинской диагностики.
Заметим, что врач не выбирает больных, которые к нему обращаются; в этом смысле "выбор" больного оказывается случайным. Заметим далее, что хотя очередной больной не принадлежит к данной группе, с которой связаны интересующие нас вероятности, он все-таки o живет приблизительно в тех же условиях, т. е. в той же местности, в то же время года и т. д., поэтому к нему можно подойти с теми же числовыми значениями вероятностей. Из этих замечаний следуют два важных вывода.
Во-первых, поскольку на вероятности P(dj) влияют, как было отмечено выше, многочисленные внешние факторы, для разных клиник и для разных врачей значения P(dj) должны быть различными, и, кроме того, они, вообще говоря, меняются во времени.
Во-вторых, возникает такой вопрос: если вероятности P(dj) так сильно зависят от места и времени, то как вообще их можно вычислить? Ответ на этот вопрос основывается на том, что, коль скоро больному поставлен диагноз определенным врачом (или в определенной клинике) в данный момент, его комплексы симптомов и заболеваний включаются в статистику, относящуюся к этому врачу (этой клинике) и к этому моменту. Иначе говоря, больной с установленным диагнозом автоматически присоединяется к данной группе, с которой связаны используемые вероятности.
Способ получения статистических данных, естественно, вытекает из вышеизложенного. Следует вести учет числа больных, имеющих любой комплекс симптомов и заболеваний. Каждый раз, когда для заданной группы больных и для заданного комплекса симптомов и заболеваний диагноз оказывается установленным точно или хотя бы с разумной степенью достоверности, количество больных в соответствующей графе списка увеличивается на 1. Когда такие списки окажутся достаточно обширными, их можно будет использовать для вычисления приближенных значений вероятностей. Следует заметить, что такие данные могут накопляться очень быстро. Например, если в поликлинику ежедневно на прием приходят 200 больных, то за месяц их пройдет более 4000; если в этом направлении будут совместно работать пять поликлиник, мы получим более 20 000 пациентов в месяц.
Для извлечения из этих статистических данных практически полезных сведений о вероятностях различных симптомов и заболеваний, необходимо их обработать, лучше всего на вычислительной машине. Чтобы имеющиеся сведения не устаревали, новые данные должны поступать в вычислительное устройство сразу, по мере их получения. Одновременно следует освобождаться от старых сведений, так чтобы в работе были все время данные, отражающие обстановку сегодняшнего дня. Весьма эффективными для нахождения нужных нам вероятностей были бы статистические методы последовательного анализа.
До сих пор мы предполагали, что для каждого больного удается установить полный комплекс симптомов и возможных заболеваний. Практически не всегда удается это сделать, и возникает вопрос об использовании неполной информации. Так бывает, когда неизвестно, обнаруживает ли больной симптом S(i) и страдает ли он определенным заболеванием D(j). В этих случаях единица должна прибавляться к каждому списку, относящемуся к такому комплексу симптомов и заболеваний, который соответствует единичным компонентам вектора булевской функции, содержащей известную частичную информацию.
Мы уже говорили, что интересующие нас статистические данные, т. е. те, которые используются для вычисления P(dj|si), зависят от местных условий и меняются с течением времени; поэтому такие данные должны собираться "локально". С другой стороны, для того чтобы статистические методы были применимы, данные должны быть "достаточно обширны", что может быть недостижимо в местных условиях. Формула Байеса помогает устранить это затруднение, поскольку для определения вероятности P(dj) нет необходимости иметь выборку столь большого объема, как для нахождения P(dj|si). Что же касается условных вероятностей P(si|dj), то они по существу постоянны, ибо не зависят ни от времени, ни от местных условий и поэтому могут быть извлечены из статистики национального масштаба, собранной за большой промежуток времени. Итак, из данных местного характера нам понадобятся лишь значения P(dj), и формула Байеса даст нам тогда искомые вероятности P(dj|si). Заметим, что собирать статистический материал о вероятностях P(dj), в которые не входят симптомы, гораздо проще, чем непосредственно вычислять P(dj|si). Отсюда ясна практическая важность для наших целей формулы Байеса.
Другая важная задача возникает в связи с редкими заболеваниями, сведения о которых, как устаревшие, могут вовсе исчезнуть из собранной статистики, относящейся к данной местности. Вопрос отпадает, если имеется специальная клиника редких болезней; в группе больных, связанных с этой клиникой, данное заболевание не будет редким. В обычных условиях графа комплекса симптомов и заболеваний, связанная с редкой болезнью, не должна давать нулевой вероятности, так как тогда можно просто упустить из виду эту болезнь. Итак, для редкой болезни должны сохраняться все статистические данные о ней, чтобы всегда существовала некоторая ее минимальная ненулевая вероятность. Последняя может оказаться завышенной, но ее использование, продиктованное соображениями предосторожности, не может привести к ошибкам тогда, когда редкое заболевание сопоставляется с частым; если же одно редкое заболевание сопоставляется с другим, также редким, то соответствующие количественные результаты могут оказаться бессодержательными.
Рассмотрим, наконец, вопрос о задержке, с которой текущая статистика отражает изменения, связанные с временем. Очевидно, что даже если мы будем с той же скоростью избавляться от устаревших статистических данных, с какой вводятся новые, то появление какой-либо эпидемии (равно как и ее ликвидация) будет зафиксировано с известным опозданием. Это явление имеет место независимо от метода получения статистических данных, и с ним приходится считаться не только при установлении диагноза, но и при решении всех других вопросов здравоохранения. Оно отражает неизбежные задержки, происходящие при сборе и обработке информации. Здесь действует некоторый "принцип неопределенности", подобный известному принципу в квантовой механике; его можно выразить неравенством
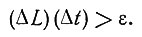
В самом деле, желая сделать статистику более чувствительной к изменениям во времени (т. е. уменьшить время запаздывания Δt), мы должны увеличить количество информации, поступающей за единицу времени, иначе говоря, собирать данные с большей области; при этом возрастает некоторый множитель ΔL, зависящий от географических условий. С другой стороны, сократив область, по которой собираются статистические данные, т. е. уменьшив ΔL, мы тем самым уменьшим скорость поступления информации; при этом для обнаружения нового явления потребуется больше времени, т. е. Δt должно возрасти. Но дело обстоит вовсе не так безнадежно, как это кажется. Существует ряд возможностей обойти подобные трудности. Так, врачам заведомо известны сезонные колебания в частоте тех или иных эпидемических заболеваний, например полиомиелита, что позволяет заранее подготовиться к сезонным эпидемическим вспышкам. Основываясь на опыте предыдущих эпидемий, можно заранее искусственно завысить некоторые вероятности и лишь через некоторое время начать использовать статистические данные, получаемые обычным путем.
4.4. Приближенные и дискриминантные методы. Естественным недостатком приближенных методов является неизбежное привнесение ошибок. Применение таких методов в процессе установления диагноза оправдывается тем, что запоминающее устройство вычислительной машины не в состоянии вместить все возможные комплексы симптомов. Но мы полагаем, что при разумной классификации областей медицины, т. е. при разумном разбиении болезней на логически независимые классы, количество симптомов и заболеваний, а следовательно, и количество комплексов тех и других, которые придется рассматривать в каждом отдельном случае, будет приемлемо с точки зрения возможностей современной вычислительной техники, так что приближенные методы не понадобятся (см. п. 2.3).
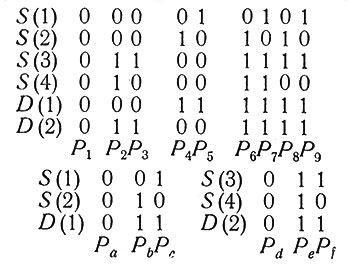
Рис. 8. Пример независимых заболеваний (потеря вероятностной информации обнаруживается в том, что в то время, как Pa, ..., Pf могут быть найдены по P1, ..., P9, обратное невозможно).
В качестве примера логически независимых классов болезней можно привести некоторые болезни ног и некоторые болезни, поражающие зрение. Мы осторожно говорим о "некоторых болезнях", так как существуют так называемые "системные" заболевания, поражающие определенные системы органов или тканей, скажем все мышцы, и тогда мышцы ног и глаз могут быть поражены одновременно; такого рода заболевания должны быть выделены в особую группу. Дадим теперь более точное определение логической независимости классов Di заболеваний. Любое заболевание D(j) может быть представлено в виде булевской функции связанных с ним симптомов S(i). Пусть Sj - объединение множеств симптомов, связанных с заболеваниями определенного класса Dj. Классы Di и Dj заболеваний назовем логически независимыми, если Si∩Sj = 0, т. е. если соответствующие классы симптомов не пересекаются. Рассмотрим, например, нижнюю часть рис. 8. Легко видеть, что
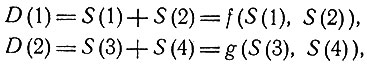
следовательно, заболевания D(1) и D(2) принадлежат к логически независимым классам*.
* (Существует регулярный метод, использующий векторное представление заболевания D(j) и позволяющий определить симптомы, которые должны входить и которые могут не входить в булевскую функцию, представляющую D(j) (см., например, стр. 326-329 и стр. 364-365 книги, указанной в сноске на стр. 151). Этот метод может быть применен для изучения групп заболеваний, входящих в независимые классы.)
Таким образом, для представления заболеваний в виде булевских функций мы можем использовать меньшие базисы, состоящие из заболеваний одного только класса, и при этом логическая информация не теряется. Однако мы теряем некоторое количество вероятностной информации, так как заболевание одного класса может создать предрасположение к заболеванию другого класса. Взять хотя бы тот же пример одновременного заболевания ног и глаз: при пораженном зрении увеличивается вероятность повредить ногу. Впрочем, такая потеря информации несущественна, во-первых, потому, что практически не встречаются случаи, когда нужно сделать выбор между различными комбинациями независимых заболеваний; во-вторых, лечение независимых заболеваний также, вообще говоря, проводится независимо. Следовательно, вероятности комбинаций независимых заболеваний не понадобятся.
Здесь целесообразно отметить некоторые приближенные приемы, которыми можно пользоваться, и тщательно взвесить связанные с ними неудобства и опасности. Неудобства могут быть двух родов: первые могут помешать логическому анализу, вторые - уменьшить точность теоретико-вероятностных оценок. Более опасны первые, так как, исказив результат логического анализа, они могут привести к ошибочным выводам, что совершенно нетерпимо.
Чтобы не исказить логический анализ, важно сохранить все симптомы и исследования, которые приводят к различным диагнозам. Поэтому приближенные приемы должны заключаться в изъятии тех столбцов, соответствующих комплексам симптомов, отсутствие которых не вызывает утраты логической информации. Мы рассмотрим вкратце три таких приема.
Первый состоит в употреблении первичных импликантов. Как было сказано выше в п. 2.3, никакой потери логической информации при этом не происходит. Заметим, что вероятность, соответствующая такому импликанту, равна сумме вероятностей всех столбцов, которые образуют этот импликант. Отсюда следует, что на значении вероятности не скажется, войдет или не войдет в столбец первичного импликанта симптом, соответствующий числу 2. Конечно, когда применяется формула Байеса и имеется таблица значений P(si|dj) для всех компонент первичного импликанта, никакие приближенные значения вероятностей не нужны.
Второй прием основан на том, что комплексы симптомов любой данной болезни обычно группируются вокруг некоторой "типичной" комбинации симптомов. Назовем "расстоянием" lik между двумя комплексами симптомов si и sk число строк, на пересечении с которыми столбцы, соответствующие si и sk, имеют различные элементы. Эта метрика удовлетворяет, очевидно, условиям
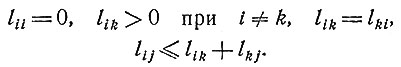
Пусть теперь di и dk - два различных комплекса заболеваний, для которых si и sk соответственно служат "типичными" комплексами симптомов. Это означает, что, каковы бы ни были комплексы симптомов sh и sj, относящиеся соответственно к di и dk, для них
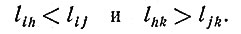
Тогда очевидно, что для того, чтобы провести различие между di и dk, достаточно ограничиться фиксацией "типичных" комплексов si и sk. Однако такая частичная фиксация симптомов может привести к ошибочному заключению. Поэтому этот прием должен применяться для исключения лишь маловероятных столбцов, "близких" к другим столбцам, связанным с тем же комплексом заболеваний. Поскольку столбцы "близки", они различаются лишь по малому числу симптомов, и вероятность того, что частичная фиксация симптомов приведет к ошибке, мала.
Третий прием представляет собой уточнение предыдущего, но теперь оставшимся столбцам приписываются определенные веса. Этот метод близок к методам максимума правдоподобия или минимального риска, применяемым в таких вопросах, как выбор оптимального решения, распознавание образов и теория самоорганизующихся систем*. Каждому элементу ekij, соответствующему симптому S(k) из комплекса Cij. приписывается вес Wkij, а вероятностям Pij - значения Vij.
* (См., например, Minsky M., Steps towards artificial intelligence, Proc. IRE., 49, № 1 (1961), 8-30; Hawkins J. K., Self-organizing systems - A review and commentary, Proc. IRE., 49, № 1 (1961), 31-40, В обеих статьях приведена обширная библиография.)
Делается это следующим образом. Сначала все Wkij приравниваются 1. Затем всякий раз, когда исключается столбец Crt, соответствующий некоторому комплексу симптомов и заболеваний, для тех систем индексов, при которых ekij = ekrt, вес Wkrj получает приращение ΔWkrj при j=t, а при j≠t - приращение - ΔWkrj. После этого вероятности Pij нормируют и через Vij обозначают их новые значения. При каждом исключении столбца все эти операции повторяют и Pij каждый раз заново нормируют. Теперь мы опишем те четыре этапа, на которые распадается процедура установления диагноза после того, как для каждого элемента определен его вес.
- Для каждого столбца, содержащегося в запоминающем устройстве, образуется сумма тех Wkij, которые согласуются с симптомами, обнаруженными у больного. Обозначим через Qj сумму Wkij по некоторым i.
- Каждая сумма Qj сравнивается с произведением a*n, где n - число симптомов, замеченных врачом, и 0<a≤1.
- Для любого комплекса заболеваний dj образуется сумма Rj вероятностей Vij, соответствующих тем столбцам, для которых сумма всех Wkij не меньше чем a*n.
- Наибольшая из сумм Rj указывает тот комплекс заболеваний dj, которым вероятнее всего страдает больной.
Заметим, что конкурирующего диагноза может и не быть: если возможно установить точный диагноз, то только он и появится в итоге описанной процедуры.
Интересно отметить, что если ни один столбец не исключается, то все Wkij = 1, a = 1 и Vij = Pij, как и следовало ожидать; в этом случае применим описанный выше первоначальный метод установления диагноза.
5. Выбор лечения с учетом эффективности
5.1. Роль эффективности. Если после проведения всех возможных исследований налицо оказываются несколько конкурирующих диагнозов, то необходимо сравнить эффективность соответствующих методов лечения. Так же приходится поступать и тогда, когда решается вопрос, идти ли на более сложные исследования или остановиться на диагнозе, который можно поставить при имеющихся результатах анализов.
При определении эффективности того или иного курса лечения приходится сталкиваться с факторами, трудно поддающимися учету, так как во многих случаях могут действовать социальные, экономические, этические и моральные соображения, относящиеся к самому больному, его семье и к обществу, в котором он живет.
Предположим, что все эти деликатные факторы каким-то образом учтены. Вопрос о разумном выборе лечения все же остается. Часто речь идет о применении сравнительно простых, широко распространённых терапевтических средств. Но, может быть, так же часто выбор средств лечения требует разбора сложной и противоречивой ситуации. Мы рассмотрим случаи*, когда решение принимается а) в бесспорной ситуации, б) в условиях риска и в) в условиях неизвестности.
* (Luce R. D., Raiffa H., Games and decisions, New York, 1957. (Русский перевод: Льюс Р. Д., Райфа, Х., Игры и решения, ИЛ, М., 1961.))
5.2. Выбор метода лечения в различных условиях. Под "выбором метода лечения в бесспорной ситуации" понимается выбор, который делается в предположении, что комплекс заболеваний пациента точно известен, а также известны прогнозы возможных способов лечения. В простейшем случае задача может быть оформлена, например, в виде таблицы
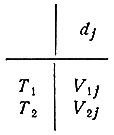
где dj - комплекс заболеваний, T1 и T2 - возможные методы лечения, V1j и V2j - соответствующие меры эффективности (согласно прогнозам) этих методов. Разумеется, всегда выбирается тот метод, мера эффективности которого максимальна. Впрочем, более сложные задачи о выборе лечения требуют применения методов линейного программирования. Рассмотрим такой пример: имеются две возможности лечения рака - лучевая терапия и химиотерапия, причем эффективность того и другого метода выражена в некоторых общих единицах; скажем, химиотерапевтический препарат обладает эффективностью в 1000 единиц на единицу веса, а облучение 1000 единиц в минуту. Допустим, что больному требуется не менее 3000 единиц эффективности. Однако оба метода токсичны, причем, опять-таки в каких-то общих единицах, токсичность лекарственных средств составляет 400 единиц на единицу веса, а токсичность облучения 1000 единиц в минуту. Допустим, что больной не должен получить более 2000 таких единиц. Наконец предположим, что введение одной единицы веса лекарственного препарата причиняет больному в три раза большие неудобства, чем облучение в течение одной минуты. Задача состоит в подборе такого сочетания обоих методов лечения, которое удовлетворяет двум сформулированным выше требованиям и одновременно минимизирует причиняемые больному неудобства. Если X1 - прописанное больному количество лекарственного препарата (в рассматриваемых единицах веса), а X2 - длительность облучения (в минутах), то прежде всего должно быть выполнено неравенство
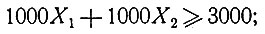
с другой стороны, токсические свойства лекарства и облучения выдвигают ограничение
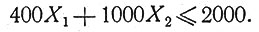
Мы хотим выбрать такие значения X1, X2, которые удовлетворяют этим двум неравенствам и одновременно минимизируют величину
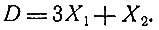
Так как, кроме того, X1≥0 и X2≥0, то искомая точка (X1, X2) должна принадлежать заштрихованной области на рис. 9. Очевидно, далее, что решение (X1, X2) должно лежать в одной из вершин заштрихованного треугольника. Вычислим значения D = 3X1 + X2 в этих вершинах, т. е. в точках (3,0), (5,0) и (5/3, 4/3); получим соответственно D = 9, D = 15 и D = 6,3. Таким образом, следует назначить комбинированное лечение - введение 5/3 единицы лекарственного препарата и облучение в течение 4/3 минуты. Конечно, приведенный пример совершенно нереален, но лишь из-за чрезмерного упрощения, присущего всякой иллюстрации. В реальных задачах приходится сталкиваться с множеством факторов и рассматривать системы многих неравенств. Но сейчас мы хотим подчеркнуть, что даже в бесспорной ситуации возникают экстремальные задачи, требующие привлечения методов линейного программирования.
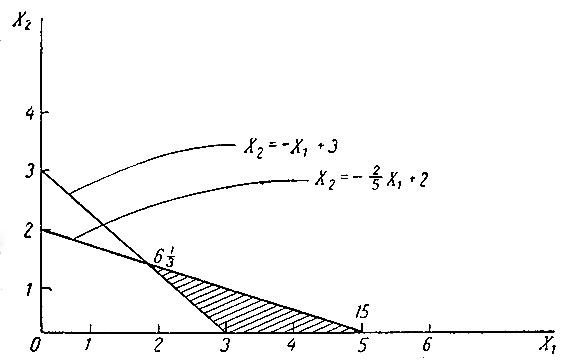
Рис. 9. Решение задачи о совместном применении лекарства и облучения
Говоря о "выборе лечения в условиях риска", мы имеем в виду, что есть несколько конкурирующих диагнозов, обладающих известными вероятностями. При этом известны меры эффективности Vkj различных методов лечения Tk одного и того же комплекса заболеваний dj, которым с вероятностью Pj страдает больной. Пусть, например, высказаны два конкурирующих диагноза, d2 и d3, соответственно с вероятностями P2 = 5/7 и P3 = 2/7. Предположим, что мы располагаем методом лечения T1, имеющим 90 %-ную эффективность при заболевании d2 (т. е. V12 = 90/100) и 30 %-ную эффективность при заболевании d3 (V13 = 30/100). Пусть одновременно имеется метод лечения T2, обладающий всего лишь 10%-ной эффективностью при заболевании d2 и 100%-ной эффективностью при заболевании d3 (т. е. V22 = 10/100 и V23 = 100/100). Перечисленные данные собраны в табл. 2. Требуется установить, какой метод лечения предпочтительнее. Ответ на этот вопрос дает понятие математического ожидания процента больных, излеченных рассматриваемыми методами:
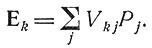
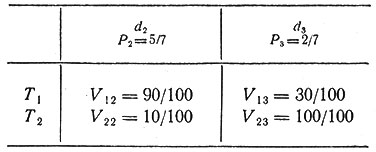
Таблица 2
В нашем примере E1 = 51/70, E2 = 25/70, так что нам следует отдать предпочтение методу T1.
До сих пор мы принимали за меру эффективности лечения данного комплекса заболеваний процент больных, излеченных этим методом. Такой подход не всегда оправдан; так, например, многие хирургические операции сопряжены с определенным риском: если операция проходит успешно, больной выздоравливает (или по крайней мере операция идет больному на пользу); в случае неудачи больной может погибнуть. При таких условиях определить меру эффективности лечения труднее. В примере, содержащемся в табл. 3, значения меры эффективности заключены между -10 и +10. Здесь E1 = 5/7, E2 = -9/7, и мы выбираем метод лечения T1.

Таблица 3
Два пункта требуют дополнительных замечаний. Во-первых, мы рассматривали нашу задачу с точки зрения множества больных, каждому из которых поставлен диагноз d2 и d3, и показали, как выбрать такой метод лечения, чтобы число излеченных больных было наибольшим. Но в частной практике врач обычно имеет дело с единичным больным. Нетрудно видеть, что, добиваясь увеличения математического ожидания числа излеченных больных, мы тем самым увеличиваем вероятность излечения индивидуального больного; следовательно, описанные методы применимы и к единичным больным.
Во-вторых, мы не ставим перед собой задачу принятия решений, связанных с учетом ценности того или иного метода лечения. Фактически мы отделили задачу выбора стратегии от задачи оценки эффекта лечения и рассматриваем только первую из них. Вторая задача часто включает трудно учитываемые факторы морального и этического характера, и решение ее в конечном счете предоставляется на усмотрение врача.
Следует еще заметить, что рассматриваемые dj должны образовывать полную систему попарно несовместимых заболеваний, т. е. у больного должно быть одно и только одно заболевание из комплекса dj. Если обозначить одним значком dj совокупность всех тех заболеваний, которые не были отброшены в результате логического анализа, то высказанное условие выполняется автоматически. Аналогичному условию должны удовлетворять и Tk; это означает, что один из рассматриваемых методов лечения обязательно должен быть применен, тогда как любые два из этих методов считаются несовместимыми.
Итак, мы изложили вкратце логическую схему, лежащую в основе установления диагноза; показали, как можно найти вероятности истинности диагнозов, полученных логическим методом; описали способ, с помощью которого можно, опираясь на вычисленные вероятности, выбрать целесообразный метод лечения. Однако, как было уже замечено, мы не всегда располагаем данными, достаточными для вычисления искомых вероятностей; в применении к некоторым заболеваниям такие данные всегда будут трудно доступны. Таким образом, во многих случаях выбор метода лечения должен опираться только на логический анализ. Мы приходим к задаче "выбора лечения в условиях неизвестности", т. е. в такой ситуации, когда имеется несколько конкурирующих диагнозов, но нет никаких данных о вероятностях, с которыми эти диагнозы могут оправдаться.
Выбор наилучшего метода лечения при таких условиях можно описать в терминах "теории игр". Налицо два "игрока" - врач и природа. Врач пытается, основываясь на имеющихся неполных знаниях о природе, выработать оптимальную стратегию. Данные, содержащиеся в табл. 2, показывают, что "выигрывает" врач и "проигрывает" природа. Но теперь нам не известны вероятности наличия у пациента заболевания d2 или заболевания d3. Наша задача по-прежнему состоит в отыскании такого метода, который обеспечил бы излечение наибольшего числа больных, иначе говоря, максимизировал бы наименьшее возможное число излеченных больных. Фактически мы располагаем тремя возможностями:
- подвергнуть всех больных лечению T1;
- подвергнуть всех больных лечению T2;
- часть больных подвергнуть лечению T1, а остальных - лечению T2. Первые два варианта составляют так называемые чистые стратегии, третий вариант - смешанную стратегию.
Обратимся снова к табл. 2 и изберем смешанную стратегию (чистую стратегию можно рассматривать как частный случай смешанной). Пусть Q - доля больных, к которым решено применить лечение T1; тогда доля больных, к которым прилуняется лечение T2, составит 1 - Q. Если бы все больные страдали заболеванием d2, то математическое ожидание доли излеченных больных было бы равно
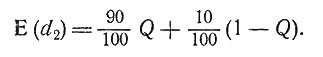
На рис. 10 нанесен график E(d2) как функции от Q. Аналогично если бы все больные страдали заболеванием d3, то мы имели бы математическое ожидание доли излеченных больных
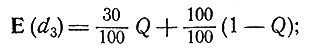
этот график также нанесен на рис. 10. Если же мы имеем как случаи заболевания d2, так и случаи заболевания d3, то значение математического ожидания излеченных больных при любом Q будет равно ординате одной из точек заштрихованной области.
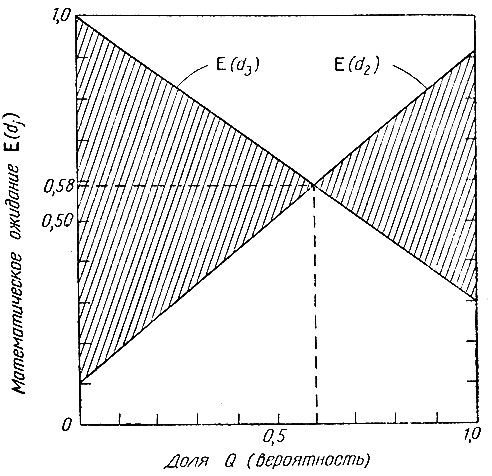
Рис. 10. Математическое ожидание в примере со смешанной стратегией
Нижний участок границы этой области соответствует наименьшей доле излеченных больных, которую мы ожидаем получить, не зная, как распределены заболевания d2 и d3. При Q = 0,6 это наименьшее значение достигает максимума, и при таком значении Q математическое ожидание доли излеченных больных составит 58% общего количества больных. Следовательно, к 60% больных следует применить лечение T1, а к 40% - лечение T2.
Осуществить такую рекомендацию весьма просто - разделить случайным образом всех больных на две группы, содержащие соответственно 60% и 40% общего числа больных; первая группа подвергается лечению T1, вторая - лечению T2. Можно действовать иначе, выбирая для каждого больного лечение T1 или T2 случайно. Действительно, второй метод оказывается единственно возможным, когда речь идет об одном больном (которого нельзя разделить на две части в отношении 6:4!). Именно так применяется смешанная стратегия в тех случаях, когда речь идет об индивидуальном больном.
Такой метод выбора лечения трудно оценить по достоинству при первом знакомстве с ним, но как раз так применяются в отдельных случаях теоретико-вероятностные соображения. Конечно, только что рассмотренный пример крайне схематичен, в реальных условиях выбор метода лечения оказывается гораздо сложнее, поскольку на практике обычно ищется дополнительная информация сверх той, которой мы располагаем в этом примере. В заключение мы процитируем высказывание Дж. Вильямса* о роли теории игр:
* (Williams J. D., The compleat strategyst, New York, I960, p. 217. (Русский перевод: Вильяме Дж. Д., Совершенный стратег или букварь по теории стратегических игр, изд. "Сов. радио", M.f 1960.))
"Теория игр, несмотря на ее ограничения, имеет в настоящее время приложения. Однако основная заслуга теории игр в том, что она дала ориентацию людям, которые сталкиваются с крайне запутанными проблемами. И хотя теория игр не дает строгого решения этих проблем, по крайней мере в настоящее время и, вероятно, в течение неопределенного срока в будущем, тем не менее она указывает основу и направление усилий, предназначенных для их разрешения. Понятие стратегий, различие между игроками, роль случайных событий, матричное представление платежей, понятие о чистых и смешанных стратегиях и т. д. дают полезную ориентацию людям, которым приходится иметь дело со сложными конфликтными ситуациями."
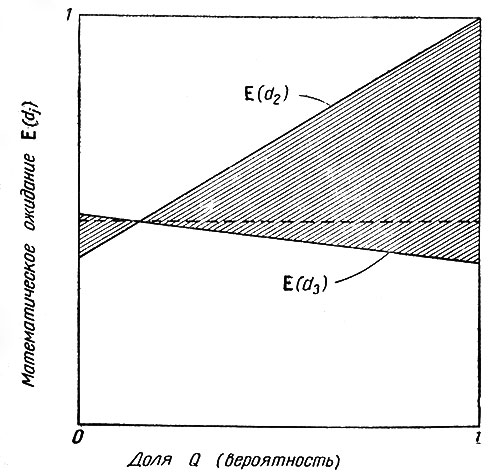
Рис. 11
Примененный здесь способ седловой точки не всегда оказывается наилучшим. Рассмотрим, например, графики на рис. 11. Способ седловой точки приведет к смешанной стратегии со значением Q, соответствующим точке пересечения графиков; однако при Q = 1 минимальное значение несколько меньше, но увеличивается вероятность больших значений Е.
5.3. Отделение факторов, трудно поддающихся учету. На значениях Vki сказывается влияние двух источников; трудно уловимые факторы и известные вероятности излечения. Последние легко учесть с помощью сбора статистического материала. Что же касается первых, то они по самой своей сути ускользают от математика или статистика. Однако задача состоит в том, чтобы оценить Vki, учитывая оба источника. Один из возможных подходов к решению этой задачи таков. В идеализированной ситуации верный метод лечения должен излечить всякого больного, страдающего данным заболеванием. Если метод лечения таков, что при известном комплексе заболеваний положительный результат достигается лишь с определенной вероятностью, большей нуля, но меньшей единицы, то это объясняется либо тем, что само лечение оказывает различное действие на различных больных, либо тем, что диагноз устанавливается не вполне точно. Первое объяснение может быть приемлемо, в частности, тогда, когда свойства применяемых лечебных средств варьируют- в значительных пределах; этот случай мы не будем рассматривать. Второе объяснение подходит, например, тогда, когда заболевание вызывается бактериями нескольких видов, которые мы еще плохо отличаем друг от друга. При этом лечебное средство может воздействовать на один вид бактерий и не воздействовать на другой, создавая впечатление случайности в исходе лечения, тогда как в действительности случайным оказывается вид бактерий, вызвавших заболевание. При этом неопределенность исхода лечения сводится к неопределенности, которая может быть устранена путем дальнейшего уточнения диагноза. Тем самым удается выделить "в чистом виде" такие Vkh значения которых полностью зависят от факторов, трудно поддающихся учету.
Пусть, например, мы имели возможные диагнозы d1, d2 с известными вероятностями P1 и Р2. Пусть, далее, Р1 и P2 - соответственно вероятности, с которыми лечение T1 применяется с успехом при заболеваниях d1 и d2. Эти первоначальные данные могут быть сведены в таблицу

Здесь значения fji(pji, -) отражают влияние вероятностей pji и трудно уловимых факторов. Вспоминая сказанное выше, введем вместо d1 комплексы заболеваний d1' и d1", а вместо d2 - комплексы d'2 и d"2. Их вероятности будут соответственно равны P1p11, P1(1-p11), P2p12 и P2(1-p12). Таблица примет следующий вид:

Здесь значения Vji' и Vji" зависят теперь уже только от не поддающихся учету факторов.
6. Динамическая задача
6.1. Описание задачи. Предположим, что после проведения логического анализа для данного больного возможны различные диагнозы; допустим, что вычислены вероятности этих диагнозов и выбрано определенное лечение. Ясно, что первые показатели воздействия на больного лечения дают дополнительную информацию о возможных диагнозах и что по прошествии некоторого времени может потребоваться пересмотреть выбранный метод лечения. В своей практической деятельности врачи постоянно используют этот цикл "лечение-диагноз", в котором метод лечения играет роль дополнительного исследования. Особенностью такого дополнительного исследования является то, что источником информации оказывается воздействие лечения на состояние здоровья больного.
В предыдущем разделе рассматривался случай, когда для возможных методов лечения были определенные вероятности их успешного применения при данном заболевании и когда с каждой комбинацией "диагноз - лечение" связывалась некоторая ее числовая оценка. Там была сделана попытка выяснить смысл случайности в исходе лечения. В настоящем разделе вероятности излечения имеют обычный смысл. Говоря точно, pkj есть вероятность изменения состояния больного, т. е. перехода от плохого состояния к хорошему, при воздействии лечения Tk на определенный комплекс заболеваний dj. Ясно, однако, что при оценке эффективности лечения можно рассматривать не два, а большее число состояний больного. В целях иллюстрации рассмотрим три состояния H1, H2, H3. При этом для каждого комплекса заболеваний и для каждого метода лечения мы будем иметь девять вероятностей перехода от любого Hr к любому Ht. Мы обозначим их prtkj, где верхние индексы указывают исходное и окончательное состояние, а нижние, как и раньше, относятся к методу лечения и к комплексу заболеваний. С каждой вероятностью возможного перехода от одного состояния здоровья к другому сопоставляется некоторое число vrtkj - "ценность" этой вероятности. В табл. 4 приведены данные, которые относятся к двум комплексам заболеваний, выступающим в качестве двух возможных диагнозов, и двум методам лечения. Если больной находится в состоянии Hr и к нему применен метод лечения Tk, то эффективность этого последнего измеряется величиной
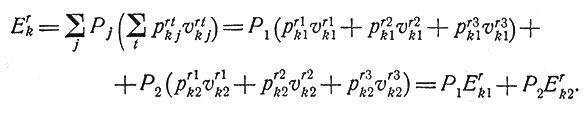
6.2. Метод динамического программирования при наличии естественного возможного диагноза. В этом разделе мы ограничимся случаем, когда имеется лишь один возможный диагноз dj, и займемся выбором "наилучшего" метода лечения этого комплекса заболеваний. Разумеется, после того как лечение применено, здоровье больного может перейти из одного состояния в другое, в связи с этим может понадобиться пересмотр метода лечения, что в свою очередь вызовет изменение состояния больного, и т. д. Выбор лечения, который обеспечивает наибольшую эффективность, производится согласно так называемому принципу оптимальности в теории динамического программирования*.
* (См., например, Bellman R., Dynamic programming, Princeton, 1957, гл. XI. (Русский перевод: Беллман Р., Динамическое программирование, ИЛ, М, 1960.) Или Howard R. A., Dynamic Programming and Markov processes (гл. З, 4), Cambridge, Mass., New York, 1960.)
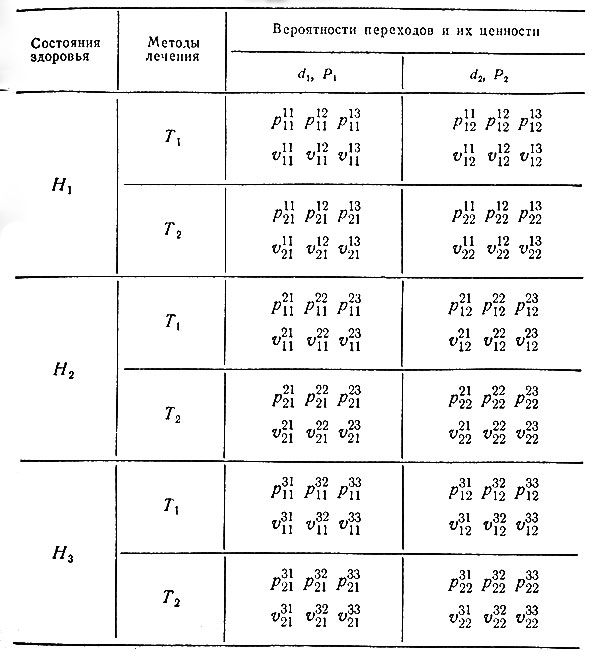
Таблица 4. (Hr - состояния здоровья больного, Tk - методы лечения, prtkj - вероятности перехода, vrtkj - их ценность, r = 1, 2, 3; k, j = 1, 2)
Пусть Vrj(n) означает суммарную меру эффективности лечения за n шагов в предположении, что Hr есть исходное состояние больного и что на каждом шаге выбирается наилучший метод лечения. Согласно принципу оптимальности,
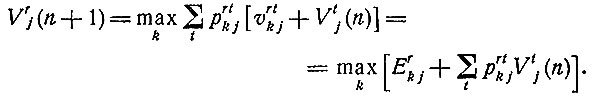
Таким образом, выбор наилучшего лечения на (n+1)-м шаге определяется значением k, при котором достигается указанный максимум.
Вычисления производятся в следующем порядке: сначала выбираются начальные значения Vrj(0) для всех r (в нашем примере r = 1, 2, 3); далее вычисляются значения
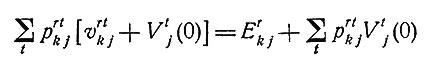
для всех r и k (в нашем случае k = 1, 2) и для каждого r находится k, при котором это выражение достигает максимума, обозначаемого Vj(1); затем вычисляются
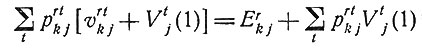
для всех r, находится k, при котором это выражение имеет наибольшее значение Vrj(2), и т. д. Пусть, например, исходное состояние больного будет Н3 (т. е. r = 3). Если V3j (n) при некотором n = n' достигает наибольшего значения, то выбор лечения рекомендуется пересмотреть n' раз. Если же Vj3 (n) возрастает вместе с n, приближаясь к некоторому предельному значению, то в качестве n' выберем какое-нибудь из n, при которых V3j(n) "достаточно близко" к этому пределу. На рис. 12 изображен график для случая, когда имеется больной с заболеванием dj. Наибольшее значение Vj3 (n) достигается при n = n' = 3; рекомендуются три цикла лечения (для n = 3, 2 и 1). Для любых r и n указаны значения k, определяющие оптимальный выбор лечения. Функция vrtkj, соответствующая методу лечения Tk, должна отражать такие факторы, как вероятность для больного остаться в живых, терапевтическую эффективность, побочное действие, связанное с длительным лечением, а также экономические, социальные и моральные соображения.
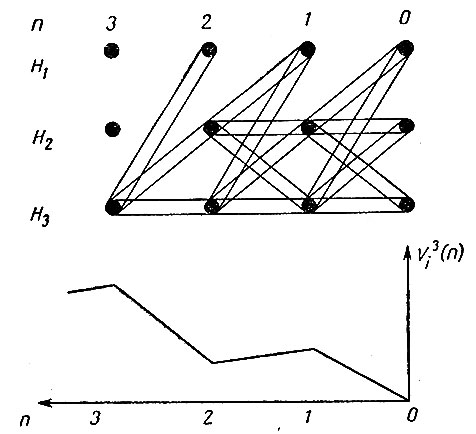
Рис. 12. Переоценка методов лечения. Больной страдает заболеванием dj, его исходное состояние H3. Предположено (для упрощения чертежа), что H1 - состояние полного выздоровления. По чертежу видно, что Vj3(n) достигает наибольшего значения при n = 3
6.3. Итерации процесса "лечение - диагноз". Пусть теперь имеются два или более возможных диагноза, и пусть они будут взаимно исключающими; каждый диагноз dj установлен с вероятностью Pj, которую можно вычислить методами разд. 4. Для каждого комплекса заболеваний dj описанным выше способом определяется число n'j планируемых циклов, а также рассматривается применение первоначального лечения на n'j-м этапе; при этом мы как бы совмещаем плоскости на рис. 12, соответствующие различным dj (см, рис. 13). Процесс итераций "лечение-диагноз" начинается с вычисления для каждого k величины
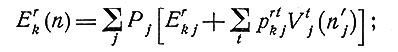
в нашем примере r = 3. В качестве исходного метода лечения мы выбираем тот метод Tk, для которого Erk (n)
оказывается наибольшей. После того как лечение применяется достаточно долго, чтобы можно было оценить его эффективность, определяется то новое состояние H'r в которое перешел больной. Это наблюдение можно использовать как дополнительный тест в логическом анализе. При этом может произойти сокращение числа возможных диагнозов, подлежащих рассмотрению. Затем вычисляются новые значения P'j вероятностей диагнозов dj. Эти вероятности используются при вычислении для каждого метода лечения Tk выражения
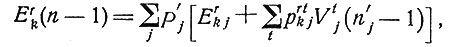
где индекс j пробегает новое, может быть, урезанное, множество значений. То k, при котором Erk(n - 1) достигает максимума, определяет новый выбор лечения, и мы продолжаем итерации согласно схеме на рис. 14.
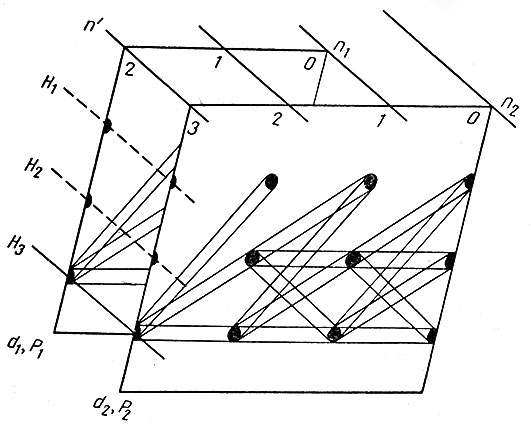
Рис. 13. Совмещение графиков, относящихся к заболеваниям d1 и d2 (итерации начаты при n'2 = 2 и n'2 = 3).
Процесс итераций заканчивается, когда число циклов n = min (n'j) будет исчерпано либо когда больной выздоровеет- смотря по тому, что произойдет раньше. Если итерации закончены, а больной еще не выздоровел, то для оставшихся комплексов заболеваний процесс повторяется точно так же, как раньше.
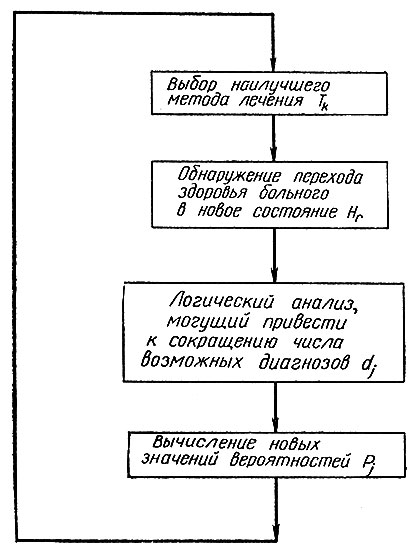
Рис. 14. Схема отдельного цикла в динамической задаче
7. Учет индивидуальных особенностей больного. Заключение
7.1. Индивидуальные особенности. Состояние здоровья определяется физиологическими и биохимическими показателями. Изменение или стандартное отклонение такого показателя у отдельного индивидуума меньше стандартного отклонения этого показателя у всей популяции, и среднее значение такого показателя у отдельного индивидуума может не совпадать со средним, вычисленным для всей популяции. Поэтому значение, лежащее в пределах нормы для популяции, может не быть нормальным для отдельного индивидуума; возможно и обратное. Вообще говоря, такого рода показатели варьируют от индивидуума к индивидууму гораздо больше, чем принято считать. Р. Уилльямс* замечает, что "практически любой человеческий организм представляет собой в том или ином смысле отклонение от нормы". Поэтому, производя какое-либо исследование, мы должны исходить из норм для данного индивидуума, а не из норм, установленных для популяции, как делают обычно. Впрочем, как указывает Уилльямс, изучение биохимической индивидуальности стало возможно лишь в последнее время с появлением таких методов исследования, как хроматография, изотопные методы и физические методы анализа и разделения.
* (Williams R. J., Biochemical individuality, New York, 1956.)
Другая причина, заставляющая нас ориентироваться на индивидуальные нормы, состоит в том, что биохимические и физиологические показатели изменяются с возрастом. Вместе с ними меняется и индивидуальная восприимчивость к той или иной болезни. Это обстоятельство ясно выступает при изучении данных о смертности: именно индивидуальные отклонения в процессе "выхода из строя", или дегенерации, различных биохимических и физиологических систем объясняют "квантовый" характер дифференциальных кривых смертности*. Обнаружив на ранней стадии этого процесса значительное отклонение какого-либо биохимического показателя от нормы, присущей данному индивидууму, можно прибегнуть к предупредительным мерам. Но в настоящее время имеется мало данных о биохимических и физиологических состояниях в начальных и последующих стадиях заболеваний.
* (См., например, статью Sacher G. A., Reparable and irreparable injury; a survey of the position in experiment and theory, в сборнике Radiation biology and medicine, под редакцией Claus W. D., Mass., 1958, стр. 297.)
Данные такого рода могут быть включены в наши схемы диагностики и выбора метода лечения. Ясно, что в том случае, когда результат соответствующего исследования может дать любое числовое значение из некоторого промежутка, последний следует заменить совокупностью дискретных значений. Ошибки, неизбежно возникающие при этом в отдельных случаях, можно устранить, если брать дискретные значения, сообразуясь с индивидуальными биохимическими и физиологическими нормами.
Вычислительная машина понадобится для фиксации значений таких показателей, периодически измеряемых у каждого больного, и для сравнения результатов измерений с индивидуальными нормами. При этом с большой точностью можно уловить сдвиги показателей, свидетельствующие о наличии патологических явлений, и своевременно принять должные меры. В этом направлении многое еще предстоит сделать, и вычислительные устройства, несомненно, принесут существенную пользу.
7.2. Практическая применимость изложенных методов. По нашему мнению, изложенные в настоящей статье методы допускают практическое применение в двух направлениях. Первое связано с обучением студентов-медиков, второе относится к применению вычислительных устройств в качестве подсобного средства в руках врача. Д-р Э. Мерфи, врач и президент Канзасского университета, отметил, что в настоящее время математики заняты переработкой самого представления о преподавании молодежи XX века современной математики. Он высказал мысль, что профессора-медики даже не подошли к проблемам эффективности педагогической техники в медицине*. Многие другие выдающиеся деятели медицинского образования также высказывали мысль о том, что практическая подготовка студентов-медиков должна в значительной мере относиться к логическим основам медицинской диагностики. Тем, кто интересуется новыми методами обучения, мы хотим показать, что современная математика содержит целый ряд дисциплин, которые могут быть использованы в преподавании медицинской диагностики нынешним студентам-медикам. В настоящей статье мы положили в основу методов диагностики понятия, относящиеся к математической логике, теории вероятностей и динамическому программированию. Мы полагаем, что эти понятия могут помочь будущим врачам быстрее и точнее использовать логику в анализе медицинских данных их будущих пациентов.
* (Anual meeting of Association of American Medical Colleges. Murphy F. D., The president's panel, J. Med. Educ, 34 (1959), 247-261.)
Могут ли вычислительные устройства практически помочь врачу в установлении диагноза? На этот вопрос сейчас нелегко ответить, и трудность заключена не в возможностях самих вычислительных машин, а в том, что понимать под их "практичностью". Будем рассуждать следующим образом: предположим, что некоторой быстродействующей электронной цифровой машине задана определенная программа, по которой эта машина должна давать сведения, помогающие установить диагноз. Предположим, что для ответа на каждый конкретный запрос врача машине предстоит произвести не более чем, скажем, 100 000 операций. Современной вычислительной машине потребуется на это около секунды. При стоимости часа работы машины 360 долларов мы получим расход 10 центов. Прибавив еще 10 центов на телефонную связь между врачом и машиной, мы получим стоимость разовой консультации 20 центов. Конечно, эти подсчеты носят лишь ориентировочный характер, но, опираясь на них, можно попытаться ответить на поставленный выше основной вопрос, который теперь можно сформулировать так: имеет ли информация, полученная при однократном использовании вычислительной машины, стоимость, существенно превышающую 20 центов? В настоящее время мы не можем ответить на этот вопрос. Отметим лишь, что вычислительная машина увеличивает возможности врача в четырех направлениях:
- она предлагает план лечения, состоящий из последовательных сеансов лечения и уточнений диагнозов, который имеет максимальную вероятность дать наибольший положительный эффект;
- указывает при этом минимальное количество необходимых для данного больного лабораторных или других исследований и процедур;
- быстро дает справку по какому-либо конкретному вопросу;
- может, основываясь на ранее собранных данных, относящихся к индивидуальному больному, объективно оценить результаты дальнейших анализов.
7.3. Сеть вычислительных устройств, обслуживающих органы здравоохранения. Гипотетическая схема такой сети вычислительных устройств показана на рис. 15. Каждая вычислительная машина обслуживает отдельных врачей и лечебные учреждения определенного района, получая, обрабатывая и передавая информацию. Все эти машины связаны со специальным вычислительным центром, который собирает данные, нужные для исследовательских и других целей. Разумеется, создание такой сети требует большой исследовательской и организационной работы*.
* (Такого рода сети, значительно более сложные, чем предлагаемая нами, используются для целей противовоздушной обороны, метеослужбы и др.)
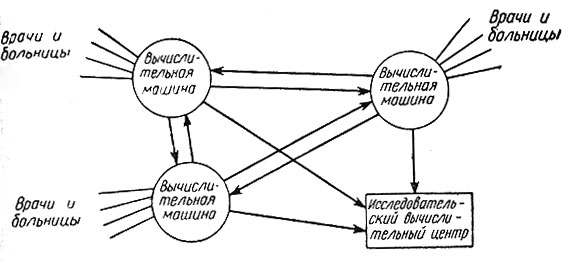
Рис. 15. Схема сети вычислительных устройств, обслуживающих органы здравоохранения
Невозможно переоценить значение такой сети вычислительных устройств для здравоохранения - не только для улучшения состояния здоровья и увеличения средней продолжительности жизни населения (что в свою очередь ведет к повышению национального дохода), но и для медицинского образования*. Насколько нам известно, в настоящее время такого рода проект не разрабатывается. Это представляется странным, так как польза такой системы очевидна, а технические возможности для ее создания более чем достаточны.
* (Подробнее об этом см. Ledley R. S., Lusted L. В., Reasoning foundatoins of medical diagnosis, Science, 130, № 3366 (1959), 9-21. (Русский перевод: Ледли Р. С, Ластед Л. Б., Объективные основания диагноза, Кибернетический сборник, вып. 2, ИЛ, М., 1961.))
Литература
- Lusted L. В., Ledley R. S., Electronic computer aids to medical diagnosis, Proc. 2nd Int. Conf. Med. Electr., Paris, 1959, 415-424.
- Ledley R. S., Lusted L. В., The use of electronic computers to aid in medical diagnosis, Proc. IRE, 47, № Ц (1959), 1970- 1977.
- Ledley R. S., Lusted L. В., The use of electronic computers in medical data processing: Aids in diagnosis, current information retrieval, and medical record keeping, IRE Trans. Med. Electr., ME-7 (I960), 31-47.
- Lusted L. В., Logical analysis in roentgen diagnosis, Radiology, 47, № 2 (1960, 178-193.
- Lusted L. В., Ledley R. S., Mathematical models in medical diagnosis, I. Med. Educ, 35, № 3 (1960), 214-222.
- Ledley R. S., Lusted L. В., Computers in medical data processing, Operations Research, 8, № 3 (1960), 299-310.
- Lusted L. В., Computer programming of diagnostic tests, IRE Trans. Med. Electr., ME-7 (1960), 225-258.
- Ledley R. S., Using electronic computers in medical diagnosis, IRE Trans. Med. Electr., ME-7 (1960), 274-280.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'