
Математические аспекты адаптивного регулирования. Роберт Калаба. Корпорация РЭНД, Санта-Моника, Калифорния
Резюме
Во многих процессах биологического, технического, экономического и статистического регулирования нужны приборы, с помощью которых можно было бы принимать решения при самых разных условиях неопределенности в отношении подлежащих регулированию физических процессов. Эти условия охватывают весь возможный интервал, включая крайние случаи полного знания и полного незнания. По мере лечения процесса регулирующей системе становится доступной добавочная информация, в результате чего эта система получает возможность "обучаться" и на основании накопленного опыта улучшать свою работу. Иначе говоря, регулирующая система может адаптироваться к окружающей ее среде.
Основная цель этой статьи состоит в том, чтобы изложить математический подход к процессам такого адаптивного регулирования, основанный на применении метода функциональных уравнений динамического программирования. Эта статья претендует на то, чтобы быть понятной читателю, не имеющему специальных предварительных познаний.
I. Введение
1. Природа адаптивного регулирования. Явление адаптации, т. е. приспособления к окружающей среде, играет в биологии важную роль. Понятие адаптивного регулирования, аналогичное понятию адаптации в биологии, быстро заняло главенствующее положение в мире автоматического регулирования. Цель этой статьи - показать, как можно применить методы функциональных уравнений динамического программирования для формулировки и решения (аналитического и численного) различных задач адаптивного регулирования [1,2].
В своей статье, опубликованной в 1933 г., В. Р. Томпсон [3] рассмотрел один интересный частный случай. Предположим, что для лечения какой-то болезни имеются два лекарства, но не известно, какое из них более эффективно. Как следует использовать эти два лекарства, чтобы спасти как можно больше больных? Если бы мы начали с обследования двух больших выборок, то с большой достоверностью смогли бы определить, какое лекарство лучше, но следствием такого способа явилось бы лечение многих больных худшим лекарством. По-видимому, более разумная процедура должна состоять в том, что сначала лекарства апробируются на небольших выборочных группах и в соответствии с наблюдениями за исходом лечения в следующем испытании отдается предпочтение тому лекарству, которое на основании имеющихся в текущий момент знаний кажется лучшим, далее процедура продолжается таким же образом. При этом, очевидно, обучение происходит в самом процессе деятельности.
Беллман и Калаба [4] рассмотрели родственные процессы, возникающие в статистической теории связи [5]. Так, для определения количества информации, проходящей по каналу связи, нужно знать статистические свойства как шума, так и сообщения. Как можно оценить это количество, если сначала сама информация недоступна и ее можно получить только путем последовательных наблюдений и их обработки?
Процессы, которые мы хотим изучить, имеют ряд интересных и новых характеристик. Они представляют собой процессы оптимизации, в которых, по-видимому, очень существенная часть информации недоступна принимающему решения. Рассмотрение таких процессов требует слияния в единое целое идей теории случайных процессов, статистики, вариационного исчисления, дифференциальных уравнений, вычислительной математики и динамического программирования. В процессах адаптивного регулирования прибор, с помощью которого принимаются решения, или контролер, вынужден работать при различных условиях неопределенности относительно регулируемого физического процесса; эти условия могут охватить весь возможный интервал, включая как полное знание, так и полное незнание. По мере течения процесса регулирующей системе становится доступной добавочная информация, в результате чего эта система получает возможность "обучаться", улучшая свою работу на основании уже накопленного опыта; т. е. регулирующая система может адаптироваться к тем условиям, при которых она работает.
Заслуживает внимания то обстоятельство, что, имея дело с такими процессами, мы должны рассматривать не только физическое состояние системы в текущий момент времени и возможные изменения в системе в результате принятия определенного решения, но также мы должны рассмотреть знания контролера о том, какие следствия вызовут принятые решения, и то, как эти знания меняются в ходе процесса. Не только контролер может оказать влияние на ход процесса, но также и ход процесса может оказать влияние на сами представления контролера о процессе. Ясно, что мы столкнулись с фундаментальным вопросом, связанным с взаимным влиянием теории и эксперимента.
В качестве первого шага рассмотрим процесс детерминированного регулирования, в котором контролер располагает всеми существенными данными. Использование метода функциональных уравнений является основой для рассмотрения процессов адаптивного регулирования, излагаемых ниже.
2. Детерминированное регулированием динамическое программирование. Предположим, что если в момент, когда система находится в состоянии с, принимается решение q, то новое состояние системы p1 будет
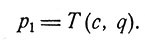
(1)
И если в момент, когда система находится в состоянии p1, принято решение q1, то система перейдет в состояние
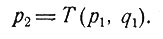
(2)
Далее, наблюдая систему в состоянии p2 и выбирая решение q2, получаем новое состояние
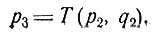
(3)
И, наконец, после N шагов система придет в состояние pN, где
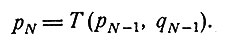
(4)
Предположим, что целью процесса регулирования является достижение конечного состояния с наименьшей стоимостью, где стоимость измеряется некоторой функцией φ(pN) от конечного состояния. Точнее, мы хотим знать целесообразное решение вопроса о том, что делать с системой, находящейся в данный момент времени в определенном состоянии, когда остается еще сделать любое заданное число шагов.
Наиболее подходящим здесь является принцип оптимальности Беллмана [1, стр. 571)].
Оптимальная последовательность решений обладает тем свойством, что независимо от исходного состояния и решения, принятого в первый момент, последующие решения должны быть оптимальными относительно состояния, получающегося из исходного в результате первого решения.
Для того чтобы применить этот принцип, введем функцию
fk(с) - стоимость k-шагового процесса (k = 0, 1, 2, ..., N), отвечающая оптимальной последовательности решений, при условии, что исходное состояние системы было с.(5)
Тогда получим уравнения
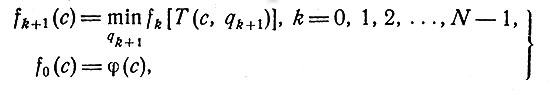
(6)
которые связывают стоимости процессов в k шагов и в (k + 1) шаг. Первое уравнение имеет следующий смысл. Когда система находится в состоянии с и осталось сделать (k+1) шагов, решение qk+1, принятое за первое, переводит систему в состояние T(c,qk+1). Тогда по определению функции fk(c) минимальная стоимость процесса в k шагов для системы с исходным состоянием T(c,qk+1) равна fk[T(c,qk+1)]. Ясно, что первое решение в (k+1)-шаговом процессе, а именно qk+1 должно быть выбрано так, чтобы минимизировать стоимость fk[T(c,qk+1)]. Это минимальное значение есть тогда стоимость (k+1)-шагового процесса при исходном состоянии с.
Если предположить, что система находится в состоянии с и предстоит еще сделать (k+1) шагов, то значение qk+1, минимизирующее правую часть первого из уравнений (6), дает оптимальное первое решение для (k+1)-шагового процесса. Решение задачи о регулировании свелось, таким образом, к решению уравнений (6), дающих как стоимости fk(c), так и оптимальные решения qk(c), k = 1, 2, ..., N.
Цель этой статьи состоит в том, чтобы показать, как можно использовать метод функциональных уравнений динамического программирования - схематически описанный выше для детерминированных процессов - в качестве руководящего принципа для формулировки и аналитического и численного изучения процессов адаптивного регулирования.
3. Другие методы. Прежде чем продолжить обсуждение вопроса, мы обратим внимание читателя на работы ряда авторов, добившихся большого успеха в исследовании сходных проблем: М. Флуд [6], С. Карлин, Р. Брадт и С. Джонсон [7], X. Роббинс [8], А. Вальд [9], Л. Задех [10], X. Роббинс и С. Монро [11], Дж. Кифер и Дж. Волфовиц [12], Н. Винер [13], Г. Бокс [14] и У. Эшби [15]. Другие ссылки можно найти в книге Белл* мана [1]; см. также библиографию П. Стромера [16]. О работе русских ученых в данной области свидетельствует, например, статья Фельдбаума [24].
Во второй части нашей статьи рассматриваются некоторые процессы, в которых не известны ни точный результат принятого решения (т. е. результат выбора контролером поведения), ни даже точное распределение этих результатов. Сначала задача рассматривается в общем виде, а потом обсуждаются два частных случая.
Третья часть относится к процессам, в которых решение должно быть принято на основании неполной информации относительно состояния системы, а в четвертой рассматриваются процессы, в которых только частично известна цель. Некоторые проблемы, представляющие в настоящее время интерес, обсуждаются в общих чертах в пятой части.
II. Частично известные преобразования
В § 2 мы рассмотрели процесс, в котором результат принятого решения точно известен контролеру. Сейчас мы хотим рассмотреть некоторые процессы регулирования, в которых исход решения точно не известен. Точнее, мы хотим рассмотреть процессы, в которых принятие определенного решения в случае, когда система находится в известном нам состоянии, приводит к новому состоянию системы, предсказать которое можно лишь в вероятностном смысле. Более того, предполагается, что контролер не знает точного распределения состояний, в которые, возможно, перейдет система после решения. Вернее, контролер имеет первоначальную оценку этого распределения и в ходе процесса регулирования он способен в свете реально наблюдаемого течения процесса изменить эту оценку. Вообще говоря, будет существовать своего рода соревнование между стремлением возможно раньше начать хорошо регулировать и желанием поскорее получить возможно больше информации о неизвестных аспектах процесса.
Сначала мы рассмотрим общий случай, затем приведем пример, когда первостепенную роль играет физическое регулирование, и, наконец, рассмотрим случай, включающий в себя последовательную оценку неизвестной вероятности, когда стоимость эксперимента меняется от шага к шагу.
4. Рассмотрение общего случая [17]. Пусть физическое состояние рассматриваемой системы обозначено буквой p - точкой фазового пространства. Кроме того, пусть состояние знаний контролера определяется информационной моделью P. Эта информационная модель содержит все те сведения о прошлом, на которых должны быть основаны последующие действия. Информационная модель может меняться от простого перечисления предыдущей истории процесса до сжатого резюме в виде задания немногих важных параметров. В последующих примерах это понятие информационной модели будет конкретизировано. Полное состояние системы и контролера обозначается точкой (p, P) нового фазового пространства.
Предположим, что если в момент, когда состояние системы есть (p, P), принимается решение q, то новое состояние физической системы будет
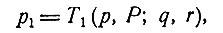
(1)
где r - случайная величина, имеющая априорное распределение G (p, P, q, r), знание которого само есть часть информационной модели. Кроме того, новая информационная модель P1 определяется преобразованием T2:
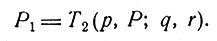
(2)
Крайне сомнительно, чтобы это преобразование можно было определить на самом деле. На современном этапе нашего развития трудно разумным образом описать как состояние знаний контролера в любой момент, так и их изменение в свете вновь поступившей информации.
Мы предположим, что физическое состояние, в которое система перешла после принятия решения, наблюдаемо, хотя, как мы увидим позднее, возникают интересные вопросы, если допустить возможность ненаблюдаемости.
Наша цель состоит в том, чтобы определить последовательность решений {q1, q2, ..., qN}, минимизирующую математическое ожидание заданной функции φ(pN, PN) конечного состояния. Так как истинные функции распределения нам не известны, то для нахождения математического ожидания мы примем априорное распределение вероятностей за истинное.
Введем далее последовательность функций
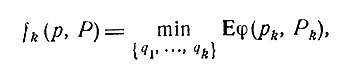
(3)
где E обозначает математическое ожидание. Тогда, как и выше, принцип оптимальности дает соотношение
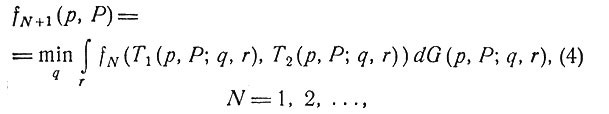
а для N = 0 мы имеем
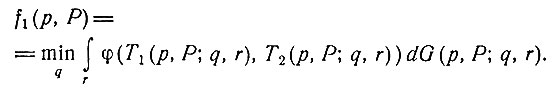
Соотношения (4) и (5) можно использовать для установления существования оптимальной политики и для получения различных свойств структуры процесса [1].
Посмотрим теперь, как можно использовать приведенные выше формулы.
5. Один частный случай процесса адаптивного регулирования. Предположим, что если в момент n система находится в состоянии xn(xn - скаляр), то в момент n+1 система будет в состоянии
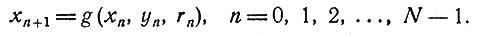
(1)
Переменная yn характеризует решение; она удовлетворяет условию
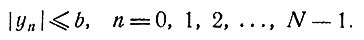
(2)
Переменные {r0, r1, ..., rN-1} образуют последовательность независимых случайных величин с одним и тем же распределением, причем rn может принимать лишь значения 1 и 0. Если обозначить через P вероятность какого-либо события, то
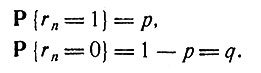
(3)
Точное значение параметра p контролеру не известно. С другой стороны, хочется предположить, что контролер делает первоначальную оценку, которая может меняться в результате наблюдения случайной последовательности {rk}.
Цель процесса - минимизировать математическое ожидание функции φ(xN) конечного состояния системы.
Теперь мы вплотную приступим к обсуждению информационной модели в случае оценки неизвестной вероятности р и к обсуждению того, как она преобразуется на каждом последовательном шаге процесса [4].
Так как вероятность р не известна, то мы будем рассматривать ее как случайную величину с функцией распределения dG(p). В том случае, когда дополнительные наблюдения дают для случайной переменной значение 1, функция распределения, согласно формуле Байеса, преобразуется в новую функцию распределения, равную 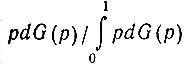 а когда наблюдение дает значение переменной rk = 0, новая функция распределения равна
а когда наблюдение дает значение переменной rk = 0, новая функция распределения равна 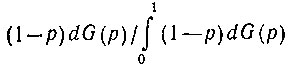 Если при дополнительных наблюдениях переменная rk принимала m раз значение 1 и n раз значение 0, то в качестве новой функции распределения следует взять функцию
Если при дополнительных наблюдениях переменная rk принимала m раз значение 1 и n раз значение 0, то в качестве новой функции распределения следует взять функцию
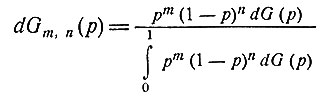
(4)
Таким образом, мы в состоянии определить информационную модель в виде двух чисел m и n, равных соответственно числу наблюдаемых единиц и нулей в случайной последовательности {rk}. Кроме того, при этом устанавливаются простые правила перехода от данной модели (m, n) к новой модели, например к (m+1,n), если в последовательности {rk} была наблюдена еще одна единица.
Далее, при отсутствии дополнительной информации мы будем принимать оценки распределения за истинные распределения и, исходя из этого, находить математические ожидания всех величин.
Мы можем теперь для k-шагового процесса с исходным состоянием с, исходной информационной моделью (m, n) и оптимальной политикой адаптивного регулирования ввести последовательность функций {fk(c; m, n)} формулой
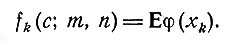
(5)
Для одношагового процесса мы имеем
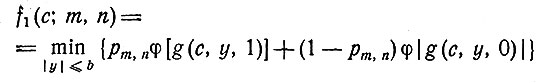
(6)
а для (k+1)-шагового процесса принцип оптимальности дает
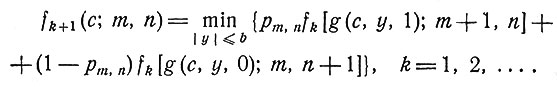
(7)
В формулах (6) и (7) простоты ради введено обозначение
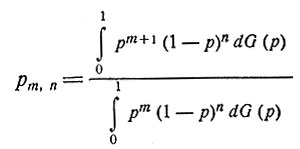
(8)
Форма подинтегрального выражения в уравнении (8) подсказывает, что исходное распределение было бы удобно считать бета-распределением.
Пусть
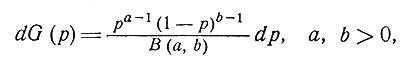
(9)
где В (а, b) - бета-функция. Тогда из уравнения (8) получим
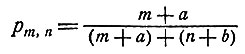
(10)
Величины а и b можно интерпретировать как априорные значения числа тех испытаний, в которых rn равно соответственно 1 и 0. Если число а + b велико, то несколько первых дополнительных наблюдений мало повлияют на оценку pm,n; если же а + b мало, то первые несколько дополнительных наблюдений сильно повлияют на априорную оценку
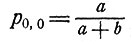
В этом случае априорная информация мало надежна.
Теперь исходная задача адаптивного регулирования сведена к решению уравнений (6) и (7). Для отыскания функций f1, f2, ... можно использовать вычислительную машину. Знание функций f1, f2, ... позволяет определить оптимальный выбор переменной у, определяющей решение для любого возможного состояния системы. К сожалению, при этом существует угроза столкнуться с расширяющейся сеткой, ибо для нахождения fk+1(c;m,n) требуются и fk(a; m+1, n) и fk(b; m, n+1). В случае когда g - линейная фикция, а φ - квадратная, что является вполне обычным допущением, аналитические методы позволяют продвинуться весьма далеко, как это показано в работе [1].
6. Процесс последовательной оценки [18,19]. Рассмотрим случай, когда контролеру приходится оценивать значение неизвестной вероятности p. Предположим, что p - неизвестная вероятность, с которой некоторая случайная величина принимает значение 1, и что (1-p) - вероятность, с которой эта же величина принимает значение 0. Контролер должен провести серию экспериментов, записать их результаты и, исходя из этих экспериментов и доступной ему априорной информации, сделать оценку p. Существует цена, связанная с проведением каждого такого эксперимента, и цена, связанная с неправильной оценкой p. Мы хотим определить, когда следует прекратить эксперимент и какую оценку следует принять контролеру. Ясно, что этот вопрос является важной общей проблемой в теории эксперимента.
С процессами последовательной оценки и родственными им процессами последовательного обнаружения приходится встречаться в вопросах связи и в радиолокации, когда приемник (т. е. получающий информацию прибор или человек) использует выборку переменной, а не фиксированной длины. Как мы увидим, принцип оптимальности дает подход к математической формулировке и численному решению таких задач.
Мы должны теперь определить процесс более детально. Предположим, что еще до начала процесса принятия решения контролер обладает априорной информацией о том, что в s испытаниях n раз будет получено значение 1. Далее, поскольку дело касается именно самого процесса наблюдения исходов, мы предположим, что в m случаях из r будет получено значение 1. Конечно, мы не используем информацию о последовательности наступления событий, но зато сильно выигрываем в простоте описания знаний контролера. Так как вероятность p неизвестна, мы будем рассматривать ее как случайную величину, функция распределения которой меняется в ходе процесса. Мы предполагаем, что если известна только априорная информация, то это распределение имеет вид
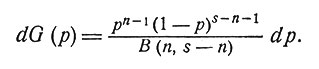
(1)
Тогда после наблюдения m единиц в r дополнительных испытаниях мы будем считать, как и ранее, что новое распределение (согласно формуле Байеса) имеет вид
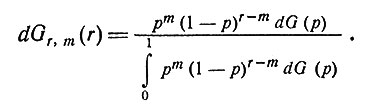
(2)
Пусть cr,m обозначает математическое ожидание стоимости неправильной оценки после r дополнительных испытаний, в которых в m случаях была получена единица. Положим
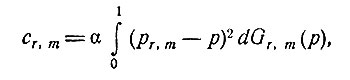
(3)
где pr,m - оценка, минимизирующая cr,m. Значение pr,m даваемое формулой
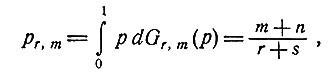
(4)
представляет собой, конечно, интуитивно разумную оценку для p. С помощью несложных преобразований получаем
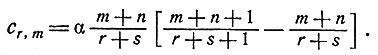
(5)
Предположим, что после осуществления m экспериментов цена следующего эксперимента равна k(m); отметим при этом, что цена одного эксперимента может меняться в течение процесса - свойство, которое приводит ко многим интересным возможностям. Предположим далее, что в случае отсутствия дополнительной информации мы в качестве истинной вероятности примем имеющуюся оценку вероятности. И, наконец, мы хотим потребовать, чтобы проводилось не более R экспериментов, так что после проведения R экспериментов процесс должен быть прекращен. Займемся теперь определением политики оптимального регулирования.
Введем функцию стоимости fr(m) и положим ее равной
математическому ожиданию стоимости процесса, в котором используется оптимальная последовательность решений и который начинается после (6) того, как в r предыдущих испытаниях m раз наблюдались единицы.(6)
Тогда принцип оптимальности приводит к функциональному уравнению
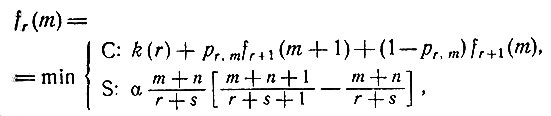
(7)
справедливому при m = 0, 1, 2, ..., r и r = R-1, R-2, ..., 0. (Здесь С означает продолжение экспериментов, а S - остановку.) Из предположения об ограниченности числа проводимых экспериментов имеем
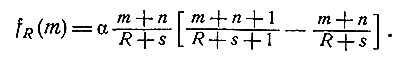
(8)
Соотношения (7) и (8) дают возможность быстро найти последовательность функций fR(m), fR-1(m), ..., f0(m). В то же самое время мы определяем, следует ли прекратить (S) или продолжать (С) проведение экспериментов и какую оценку следует принять для p в случае прекращения процесса.
Вышеприведенные функциональные уравнения были исследованы на вычислительных машинах в широком диапазоне изменения параметров α и R и для различных функций стоимости k(m). Если стоимость эксперимента не меняется в течение процесса или если она возрастает с номером эксперимента и если априорная вероятность равна 1/2, то оптимальная политика состоит по существу в следующем.
- Продолжать эксперименты, если r мало (не имеется достаточно информации для того, чтобы на ее основе дать оценку).
- Прекратить эксперименты, если r достаточно велико.
- Продолжать эксперименты, если r принимает промежуточные значения (если только не имеют место серии, состоящие из одних нулей или из одних единиц,- тогда следует прекратить эксперимент).
С другой стороны, если стоимость каждого нового эксперимента снижается согласно формуле
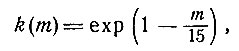
(9)
то оптимальная политика значительно более сложна. Случай n = 1, s = 2, α = 1500 и R = 40 хорошо иллюстрирует это. Когда r≤19, т. е. когда было проведено 19 или меньше экспериментов, то, вообще говоря, правило состоит в том, чтобы провести еще один эксперимент. При r между 20 и 33 правило заключается в том, чтобы немедленно остановиться и сделать соответствующую оценку. Если r заключено между 34 и 39 и приблизительно половина наблюдений дали единицу, то правило снова рекомендует провести по крайней мере еще один эксперимент. Конечно, причина такого поведения кроется в том, что цена эксперимента упала так низко, что выгодно провести по крайней мере еще один эксперимент, до того как дать оценку. Когда r равно 40, то по условию процесс должен быть прекращен.
III. Частично известные состояния
Перейдем теперь к рассмотрению ряда процессов регулирования, в которых контролер вынужден осуществлять свою деятельность, обладая только частичными знаниями о состоянии, в котором находится система. Это как раз и есть та ситуация, в которой практически находятся многие контролеры. В этом случае одна из трудностей возникает при попытке применить понятие обратной связи. Как это сделать - не ясно, ибо одна из операций в цикле обычной обратной связи заключается в измерении мгновенного состояния системы и в передаче этой информации контролеру.
Наш первый пример относится к системе, которая находится в неизвестном состоянии и которую следует перевести в заданное конечное состояние так, чтобы математическое ожидание времени перехода было минимальным. В этом примере мы имеем дело с новой формой задачи на оптимальное быстродействие [20]. Во втором примере рассматривается процесс стохастического регулирования, в котором существует определенная вероятность того, что в некоторый момент времени состояние системы ненаблюдаемо.
7. Восстановление оборудования [21]. Определенная часть сложного оборудования находится в одном из двух возможных состояний: удовлетворительном и неудовлетворительном. В начальный момент времени мы не знаем, в каком состоянии находится оборудование. Над оборудованием можно совершать две операции: операцию восстановления R и операцию проверки Т. Каждая операция для своего выполнения требует единицу времени. Результат проверки состоит в том, что точно определяется, находится оборудование в удовлетворительном состоянии или нет. Результатом операции восстановления является то, что после нее увеличивается вероятность найти оборудование в удовлетворительном состоянии. Мы хотим выполнить последовательность операций, которая минимизирует время, необходимое для приведения системы в удовлетворительное состояние и для проверки того, что система действительно находится в этом состоянии.
Для проведения дальнейшего анализа необходимо сделать несколько предположений. В частности, мы будем считать, что состояние системы в данный момент выражается вещественным числом x, где
x есть вероятность того, что система находится в неудовлетворительном состоянии.(1)
Кроме того, мы предположим, что если x - состояние системы в данный момент и что выполнена операция восстановления, то новое состояние системы есть ах, где 0<а<1.
Мы можем теперь ввести функцию f{x), положив ее равной
математическому ожиданию времени приведения системы в удовлетворительное состояние (причем должно быть известно, что оно удовлетворительное) при использовании оптимальной политики, если состояние системы в исходный момент было x.(2)
Тогда принцип оптимальности приведет к уравнению
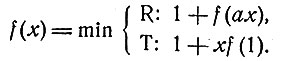
(3)
Теперь наша задача сведена к решению функционального уравнения (3).
Начнем с замечания, что существует значение x = x0, обладающее тем свойством, что если x<x0, то мы выбираем операцию проверки, а если x>x0, то выбираем операцию восстановления. Более того, для x = x0 мы имеем
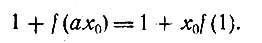
(4)
Так как
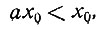
(5)
то мы должны иметь
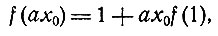
(6)
так что
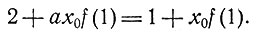
(7)
Итак, мы нашли выражение для порога x0.
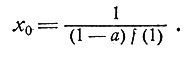
(8)
Осталось еще выразить f(1) через параметр а. Это можно сделать, поскольку должно существовать целое положительное K, для которого справедливы следующие соотношения:
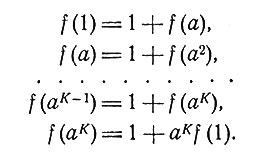
(9)
Отсюда следует, что
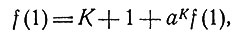
(10)
так что
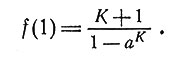
(11)
Все еще не известное значение K должно быть значением, минимизирующим правую часть уравнения (11), так что мы можем написать
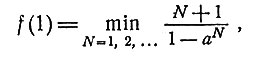
(12)
что и завершает рассмотрение вопроса. Таким образом, определен порог x0 и найдено правило оптимального решения.
8. Регулирование в случае, когда возможна ненаблюдаемость [22]. Рассмотрим процесс дискретного стохастического регулирования, в котором состояние системы в момент времени n определяется вектором состояния xn, вектор регулирования обозначается yn, а изменение состояния определяется соотношениями
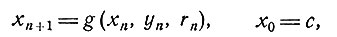
(1)
где {rn} - последовательность независимых случайных векторов с общим для всех них известным распределением. Если мы потребуем, чтобы для минимизации математического ожидания некоторой заданной функции h(xN) конечного состояния xN был использован контроль с обратной связью (представленный вектором yn), то непосредственное применение динамического программирования даст алгоритм решения. Напишем
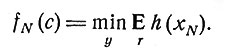
(2)
Принцип оптимальности дает рекуррентное соотношение
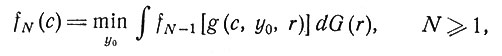
(3)
причем f0(c) = h(c). Подробное изложение этого вопроса можно найти в работах [1, 21].
Предположим теперь, что мы рассматриваем предыдущий процесс, наделенный еще следующим дополнительным свойством: на любом шаге процесса состояние системы в рассматриваемый момент времени может оказаться не известным принимающему решение. Назовем такой процесс процессом регулирования в случае, когда возможна ненаблюдаемость.
Задача об определении оптимального регулирования в ситуациях такого типа была предложена нам Дж. Крейгом (корпорация РЭНД). Как мы увидим ниже, процессы этого типа обладают некоторыми интересными и новыми аспектами и ставят сложные аналитические и вычислительные вопросы.
Так как существует возможность того, что действительное состояние системы будет оставаться неизвестным в течение нескольких последовательных шагов, мы определим состояние системы тремя числами: m, n и с. Здесь n - число шагов, которые еще предстоит сделать до конца процесса, m - номер последнего шага, на котором было точно известно состояние системы, и с - физическое состояние системы на этом шаге.
Пусть
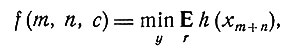
(4)
где x0 = с. Введем теперь преобразование состояний следующим образом. Мы имеем рекуррентные соотношения (1) и простоты ради зафиксируем p - вероятность того, что на любом шаге процесса мы не можем наблюдать действительное физическое состояние системы.
Пусть
zm(c) есть случайная величина, характеризующая состояние, в которое система пришла из состояния c через m шагов, в течение которых ее состояние не наблюдалось.(5)
Величина zm(c) будет зависеть от случайных векторов r0, r1, ..., rm-1 и от векторов регулирования, выбираемых в течение первых m шагов.
Принцип оптимальности приводит теперь к функциональному уравнению
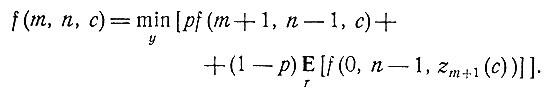
(6)
Вектор y, минимизирующий правую часть уравнения (6), является функцией от m, n и с. Положим y = ym,n(с).
Необычным в этом уравнении является именно его неявная форма (к счастью, большинство предыдущих функциональных уравнений динамического программирования было получено в явном виде). Проанализируем теперь уравнение (6).
Мы должны определить условное математическое ожидание величины f(0, n-1, zm(c)) при условии, что последним известным физическим состоянием системы было с, а потом в течение m шагов состояние системы было ненаблюдаемо. На первом шаге был выбран вектор регулирования y0,m+n (мы пользуемся введенными выше обозначениями), и это привело к состоянию системы, определяемому случайной величиной:
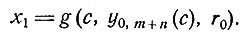
(7)
На этом шаге при отсутствии информации о действительном состоянии был выбран вектор регулирования y1,m+n-1(c) и новое случайное состояние стало
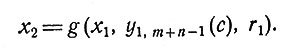
(8)
Продолжая таким же образом, получаем, что случайная величина zm(c) зависит от векторов регулирования yk,m+n-k(c), k = 0, 1, ... , m-1.
Следовательно, уравнение (6) при m + n≤N определяет функции f(m,n,c) и yk,m+n-k(с), 0≤m + n≤N, k = 0, 1, ..., m + n. Заметим, что эта система является неявной и нет простых прямых способов получить из нее явное выражение одновременно для функций f (m, n, c) и yk,m+n-k(с). Если надо получить численные решения,то, вероятно, метод последовательных приближений был бы наиболее подходящим.
Для случая когда рекуррентные соотношения (1) имеют вид
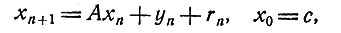
(9)
и задача состоит в минимизации 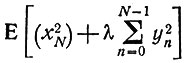 можно найти явное аналитическое выражение для функций fm,n и ym,n, но выкладки не тривиальны.
можно найти явное аналитическое выражение для функций fm,n и ym,n, но выкладки не тривиальны.
IV. Частично известные критерии
Исследуем теперь еще один тип неопределенности - неопределенности целей, которых добивается контролер. В рассматриваемом процессе контролер стремится поместить систему "в надлежащее место в надлежащее время", но не знает, где оно. Чертами такого процесса обладают различные процессы регулирования транспорта [23].
9. Частный случай процесса. Рассмотрим систему, изменение состояния которой описывается уравнениями
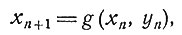
(1)
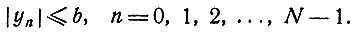
(2)
Исходное состояние системы - с.
Детерминированная задача может состоять в определении последовательности y0, y1,..., yN-1, минимизирующей |xN - d|.
Если величина d заранее не известна контролеру, но известно, что
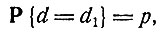
(3)
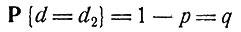
(4)
(значение р известно контролеру), то на процесс регулирования можно повлиять таким образом, чтобы минимизировать математическое ожидание величины J, которое равно
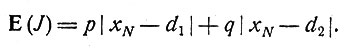
(5)
В случае адаптивного регулирования предполагается, что контролеру не известно значение р. Мы, однако, будем считать, что перед каждым решением контролер наблюдает исход аналогичного процесса и определяет, являются ли d1 и d2 конечными точками. Тогда значение р можно оценить, и, как и ранее, эта оценка равняется
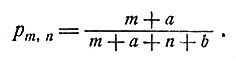
(6)
Предполагая теперь, что эта оценка используется в качестве истинного значения р, введем функцию fk(c,m,n), положив ее равной
цене k-шагового процесса, в котором использовалась оптимальная политика, исходным состоянием было c, m раз наблюдалась реализация d1 и n раз - реализация d2.(7)
Принцип оптимизации теперь дает
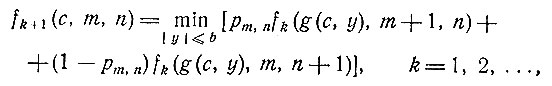
(8)
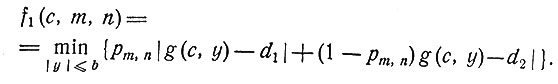
(9)
Численное решение этих уравнений довольно трудно, поскольку получается расширяющаяся сетка,
V. Обсуждение
Цель теории процессов адаптивного регулирования - определение решений, обеспечивающих оптимальное регулирование в условиях, когда существуют неопределенности, но существует также и возможность обучения. Как правило, одно лишь введение случайных величин с известными распределениями не адекватно описанию физических ситуаций, к которым предполагается применить теорию.
Существуют серьезные трудности, касающиеся самих понятий, когда мы стремимся дать точное математическое описание этих сложных процессов. Как мы видели, следует рассматривать не только физическое состояние системы и его изменения в ходе процесса, но также и состояние информации, имеющейся у контролера, и ее изменения в свете накопленного опыта. При этом мы столкнулись с задачей краткого описания истории процесса и описания изменений, которые при этом происходят. Ясно, что важную роль будут играть достаточные статистики. Более того, неопределенность может возникнуть почти неограниченным числом способов, и для рассмотрения многих из возникающих здесь задач требуется большое воображение.
Аналитический аспект рассматриваемых задач ставит множество вопросов - от вопросов сходимости решений в случае дискретного времени, решения соответствующих задач в случае непрерывного времени и до определения различных структурных свойств решений нелинейных функциональных уравнений.
Вычислительный аспект адаптивного регулирования включает в себя проблемы, связанные с большим числом степеней свободы, расширяющейся сеткой [1], устойчивостью и т. п. Ограниченная скорость и ограниченная емкость памяти современных вычислительных машин заставляют нас проявлять большую изобретательность при формулировке и анализе задачи, для того чтобы задача допускала возможность численного решения. В настоящее время мы можем сказать, перефразируя Черчилля, что адаптивное регулирование есть тайна, завернутая в головоломку, содержащуюся внутри загадки.
Литература
- Bellman R., Adaptive control processes: A guided tour, Princeton, New York, 1961. (Русский перевод: Беллман Р., Процессы регулирования с адаптацией, "Наука", М., 1964.)
- Bellman R., Kalaba R., Dynamic programming and adaptive processes: Mathematical foundation, IRE Trans, on Automatic Control, AC-5 (1960), 5-10.
- Thompson W. R., On the likelihood that one unknown probability exceeds another in view of the evidence of two samples, Biometrika, 25 (1933), 285-294.
- Bellman R., Kalaba R., On communication processes involving learning and random duration, IRE National Convention Record, 1958, часть 4, стр. 16-21.
- Bellman R., Kalaba R., On the role of dynamic programming in statistical communication theory, IRE Trans, on Information Theory, IT-3 (1957), 197-203.
- Flood M., The influence of environmental nonstationarity in a sequential decision-making experiment; Decision processes, New York, 1954.
- Karlin S., Bradt R., Johnson S., On sequential designs for maximizing the sum of n observations, Ann. Math. Statist, 27 (1956), 1061 - 1074.
- Robbins H., Some aspects of the sequential design of experiments, Bull. Amer. Math. Soc, 58 (1952), 527-535.
- Wald A., Sequential analysis, New York, 1947. (Русский перевод: Вальд А., Последовательный анализ, Физматгиз, М., 1960.)
- Zadeh L., What is optimal, IRE Trans, on Information Theory, IT-4 (1958), 3.
- Robbins H., Monro S., A stohastic approximation method, Ann. Math. Statist., 22 (1951), 400-407.
- Kiefer J., Wolfowitz J., Stohastic estimation of the maximum of a regression function, Ann. Math. Statist., 23 (1952), 462-466.
- Wiener N., Cybernetics, New York, 1948. (Русский перевод: Винер Н., Кибернетика, изд. "Сов. радио", М., 1958.)
- Box G., Evolutionary operations, a method for increasing industrial productivity, Appl. Statist, 6 (1957), 3-23.
- Ashby W., An introduction to cybernetics, New York, 1954. (Русский перевод: Эшби У., Введение в кибернетику, ИЛ, М., 1959.)
- Stromer P., Adaptive or self-optimizing systems - a bibliography, IRE Trans, on Automatic Control, AC-4 (1959), 65-68.
- Bellman R., Kalaba R., A mathematical theory of adaptive control process, Proc. Nat. Acad. Sci. USA, 45 (1959), 1288- 1290.
- Kalaba R., Computational considerations for some deterministic and adaptive control processes, RAND Corporation paper P-2210, January 1961.
- Bellman R., Kalaba R., Middleton D., Dynamic programming, sequential estimation and sequential detection processes, Proc. Nat. Acad. Sci. USA, 47 (1961), 338-341.
- LaSalle J. P., Time optimal control, Bol. Soc. Mat. Mexicana (2), 5 (1960), 120-124.
- Bellman R., Dynamic programming, Princeton, New York, 1957. (Русский перевод: Беллман Р., Динамическое программирование, ИЛ, М., 1960.)
- Bellman R., Kalaba R., Interrupted stochastic control processes, Information and Control, 4 (1961), 346-349. См. также Zadeh L., Remark on the paper by Bellman and Kalaba, Information and Control, 4 (1961), 350-352.
- Kalaba R., Some aspects of adaptive control processes, Bol. Soc. Mat. Mexicana (2), 5 (1960), 90-101.
- Фельдбаум А., Теория дуального управления, Автоматика и телемеханика, 21, № 9 (1960), 1240-1249.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'