Ситуации сохранения

Мы подходим к концу теоретических джунглей и возвращаемся к некоторым наглядным фактам. Прежде всего уточним, что подразумевается под стандартной ситуацией сохранения по Пиаже, который первым изучал эти вопросы по отношению к любым размерам.

Для начала ребенку предлагают два количества, которые выглядят равными и в действительности равны. Можно использовать непрерывные материалы (вода, глина) или псевдонепрерывные (песок, сахар, соль, а также бусинки, морковки или пуговицы, взятые в таком количестве, чтобы их трудно было сосчитать). Обычно вода, песок или фасолины даются в двух одинаковых банках с прозрачными стенками, так что содержимое можно видеть. Глину можно предложить в виде двух шаров равного диаметра.

Дискретные материалы либо предлагаются в такого же рода банках, либо их выкладывают в виде двух рядов или иной простой фигуры. Предметы используются или в небольших количествах, чтобы был возможен счет, или в такой форме представления, при которой легко осуществляется установление попарного соответствия, т. е. два ряда выкладываются параллельно, чтобы было видно, что они одинаковы. Давать указания и следовать им легче, если эти два ряда бусинок или ракушек имеют разную окраску.

Для простоты изложения будем пока говорить о работе с водой. Легче задавать вопросы, особенно маленьким детям, если обе банки обозначены, как "твоя" и "моя" банка. "Это твоя банка, это - моя". Первоначальная эквивалентность устанавливается тем, что в каждую банку наливается одинаковое количество воды из стандартного сосуда, объем которого меньше объема банки. Так как банки прозрачны, то ребенок легко может видеть, что в обеих банках вода стоит на одинаковых уровнях. Соответствующие операции может проделывать как взрослый, так и ребенок, но следует отметить, что с точки зрения ребенка небезразлично, кто это делает: когда он измеряет и переливает сам, то он знает, что "взрослые колдовства" не повлияют на результаты. Имея две банки, заполненные таким образом, взрослый задает первый вопрос, чтобы удостовериться, что ребенок видит и сознает их эквивалентность: "Как ты думаешь, у нас одинаковое количество воды или у одного из нас больше?" Если он не способен увидеть, что у вас обоих одинаковое количество, то нет смысла продолжать. Предположим, что он может установить первоначальное равенство. Тогда следующим шагом будет переливание содержимого одной из банок в другую банку с отличающимся диаметром. Переливают "твое" или "мое", имеет третья банка больший или меньший диаметр, переливает сам ребенок или взрослый - все это может иметь значение. Вы можете сказать: "Теперь я собираюсь перелить мою воду в эту банку", переливая содержимое в банку большего диаметра, так что то же самое количество воды достигает более низкого уровня.

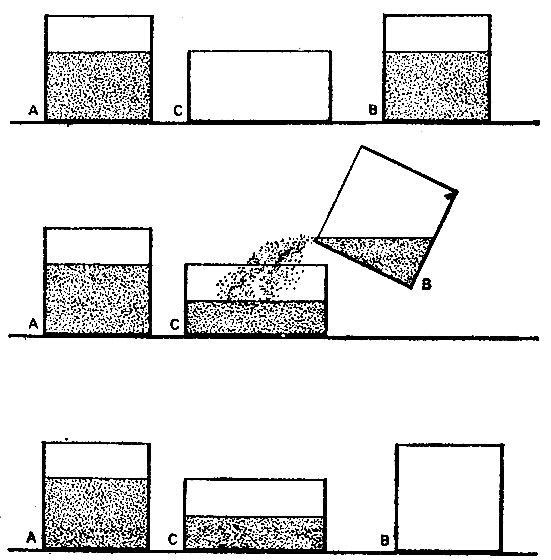
Рис. 24

Следующий вопрос: "У нас обоих все еще одинаковое количество воды или у одного из нас больше?" Любимый обходной путь, если ребенок не может сказать одинаково, это: "У нас обоих больше". Если он говорит, что у вас обоих все еще одинаково, или предлагает другие приемлемые формулировки, то можно задать последний вопрос: "Откуда ты знаешь?" Ребенка можно считать способным понимать сохранение лишь в случае, если он может привести причину. Не очень хорошо, если он будет просто отстаивать: "Я знаю, что это так" или "Потому что это так". Ответ будет обоснованным, если малыш либо отсылает к первоначальному равенству: "Потому что мы налили в каждый из них одинаково", либо принимает в расчет изменение внешнего вида: "Потому что эта банка шире, но ниже". Менее подходящи, но также допустимы мотивировки, которые содержат ссылки на принцип обратимости или включают замечания о том, что ничего не было добавлено или отнято. Строго говоря, согласно канонам логики, единственно правильным аргументом будет комбинация первоначального равенства и того, что ничего не добавлено и не убавлено. Редко ребенок сможет представить подобную утонченную и непробиваемую линию доказательств. Сойдет любая из четырех перечисленных мотивировок.

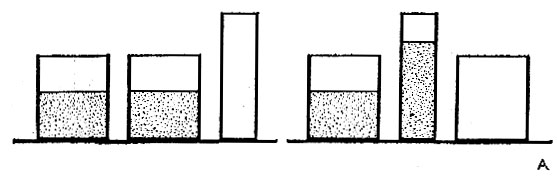
Рис. 25

Такие же действия следует провести с материалами различного вида (глиняные шарики можно раскатывать в колбаски или сплющивать в лепешки) и с разделением количеств (материалы переливаются из одной банки в две другие). Дискретные количества можно поместить в банки и пересыпать из банки в банку или разложить в параллельные ряды, причем один ряд может быть удлинен, укорочен или раздроблен, чтобы изменить его внешний вид (примеры даны на рис. 25-31)

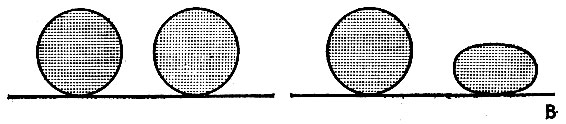
Рис. 26

Если ребенок разбирается во всех этих ситуациях и отвечает удовлетворительно на все три вопроса, то считается, что он способен понимать сохранение. Ему может исполниться 8 лет, а в ряде случаев даже больше, прежде чем он освоит понятие сохранения на этом уровне сложности. Наша забота - сделать так, чтобы развитие ребенка не задерживалось из-за того, что у него не было возможности заострить свое воображение и направить свою энергию в нужную сторону в ситуациях, определяемых его все время меняющимися способностями, интересами и аппетитами.

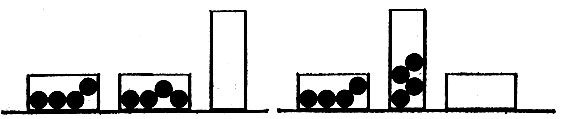
Рис. 27

Пример Тоби (5 л. 4 мес), уровень развития которого во многих отношениях был немного выше уровня развития сверстников, показывает, насколько далеко усвоение понятия сохранения отстоит от положения все или ничего. Он справлялся со всеми приведенными выше заданиями, включая преобразования с разделением количества. Однако его ставила в тупик ситуация В на рис. 26. Тоби отвечал правильно, если второй глиняный шар был лишь чуть-чуть деформирован. Однако, если деформация превышала некоторый предел, он не мог более применять сохранение. Когда шар раскатывали в очень длинную колбаску, он полагал, что теперь в ней больше, чем в шаре. Когда ее скатывали так, что она приобретала первоначальный вид, она сразу же становилась для него такой же. Почему он терялся в этом частном случае - это тема для размышлений.

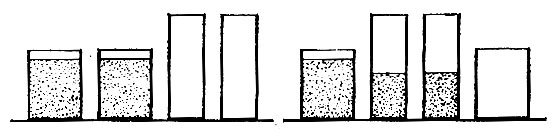
Рис. 28

В предыдущих главах мы приводили ПУСы, проясняющие меняющиеся значения слова одинаковый. В эти ПУСы были введены те типы характеристики внешнего вида и те типы операций, которые допускают употребление этого многозначного слова. Другие ПУСы вводят принципы и средства, упомянутые в тех разделах главы 1, которые посвящены оценке состояний и преобразований. Чтобы ответить на первый из трех вопросов в стандартной ситуации сохранения, ребенок должен подбирать пары, устанавливать попарное соответствие или же считать по биркам. В случае непрерывных количеств, помещенных в банках, первоначальная эквивалентность устанавливается сравнением их внешнего вида, а в случае дискретных материалов, расположенных в ряды,- счетом по биркам, или установлением попарного соответствия, или же, когда используются малые числа, субитированием.

Рис. 29

При постановке второго вопроса, следующего после того, как одно из количеств преобразовано, ребенок больше не может их сравнивать по внешнему виду, а установление попарного соответствия становится для него затруднительным. К дискретным количествам все еще приложим счет по биркам, а в случае малых чисел достаточно непосредственного восприятия. Можно привлечь любые приемы, указанные в главе 1; однако никакой из них не будет нужен, если ребенок опирается на основной принцип сохранения - ничего не добавлено и ничего не убавлено, в то время как способность дать приемлемый ответ на последний вопрос зависит от того, насколько он усвоил этот принцип. Для правильного ответа на второй вопрос не нужны никакие операции. Все же вы обнаружите, что вначале ребенок чувствует необходимость применить те или иные операции к преобразованному количеству, когда перед ним поставлен вопрос: "У нас обоих все еще одинаково?"

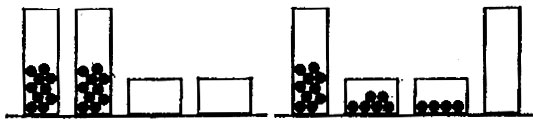
Рис. 30

В этом логическом парадоксе может быть заключен, секрет истинного сохранения. Если операции не нужны, зачем их использовать? Существуют, по крайней мере, две возможные причины, почему он обращается к операциям, когда осваивает концепцию сохранения. Во-первых, он должен сначала использовать такие операции, как счет, чтобы обнаружить, что внешние признаки могут вводить в заблуждение. Во-вторых, он должен использовать эти операции для того, чтобы открыть, что они не имеют отношения к главному выводу - сохранению тождественности данного количества, к которому ничего не добавлено.

Рис. 31

Как помочь ребенку сделать эти два чрезвычайно важных открытия? В том, что касается первого вопроса, мы уже построили значительную часть фундамента. ПУС 39, например, привел нас к тому, что, наблюдая, как вы кладете 3 бусинки на блюдце, он научился класть такое же число на другое блюдце. Он может проделывать это с помощью непосредственного восприятия троичности, установления попарного соответствия или счета по биркам. Не важно, какой метод он использует. Поскольку он устанавливает эквивалентность самостоятельно, прибавляя один объект за другим и продвигаясь к большим числам, он достигнет предела непосредственного восприятия, как в ПУСах 54 и 56.

Выше этого предела он может использовать попарные соответствия, но счет по биркам более эффективен в тех заданиях, которые требуют более долгого решения; такие задания входят в ПУСы 62-65. Наверное, вы видите, к чему ведет обсуждение понятия тождественности, начатое ранее в этой главе. Наша цель - использовать счет по биркам, связанный с его собственной тождественностью, чтобы перекинуть мост между малыми числами, которые могут быть восприняты непосредственно, и большими числами, к которым мы приходим только при счете. От числа 2, ассоциированного с двоичностью его ног, через число 5, ассоциированное с пятиричностью пальцев на одной ноге, он переходит к числу 10 и одновременно к десятиричности, ассоциированной со всеми пальцами ног, взятыми вместе. После того как ребенок освоил количественное свойство малых чисел путем непосредственного восприятия в сочетании со счетом по биркам, он должен обобщить эту операцию и принцип на большие числа, связанные с большими множествами, которые не поддаются субитации. Как только ребенок подготовлен к путешествию в неизведанное и начинает наряду с тождественностью использовать число для подтверждения того, что количество сохраняется, становится возможным привлечь внимание к другому ошеломляюще простому факту. Так как число не изменяется, пока ничего не добавлено и ничего не убавлено, то вообще нет надобности считать.

Поэтому мы стремимся к тому, чтобы ребенок использовал счет, поскольку дело касается дискретных количеств, чтобы установить исходную эквивалентность и правильно ответить на первый вопрос, чтобы он применял сохранение, количества, не проверяя его счетом, а сознавая, что эта проверка не нужна. Чтобы сделать это, он должен пренебречь любыми искажениями формы и внешнего вида как не относящимися к делу и только замечать, что ничего не было добавлено или убавлено. Парадоксально, что он должен научиться технике счета по биркам для того, чтобы открыть, что счет вообще не нужен.

Непрерывные материалы ставят большие проблемы, поскольку они не предоставляют случая применить счет как мостик. Объемы могут быть измерены при помощи средств, которые не всегда имеются под рукой, или с помощью разбиения количества на части и использования малого сосуда в качестве стандартной меры. Простые площади, разграфленные на квадратики, представляют шаг в этом направлении, и они были использованы в предыдущей главе для закрепления идеи о том, что непрерывному двухмерному количеству (площади) можно приписать число. Каждая пластинка обладает и качественной тождественностью "вещи самой по себе", и непосредственно воспринимаемой количественной тождественностью, связанной с пластинкой. Переворачивая пластинку обратной стороной, мы убираем числовой признак. Естественно напрашиваются вопросы: разве число, ассоциированное с пластинкой, изменяется или исчезает только потому, что оно больше невидимо? Или качественная тождественность пластинки несет в себе количественную идентичность, тождественность числа, ассоциированного с ней, даже в том случае, когда прямой признак числа удален? В принципе можно придумать аналогичную ситуацию, использующую вместо площадей объемы, но она эта бы чересчур искусственной и имела бы сомнительную познавательную ценность. Важна сама идея, а рациональное зерно этой идеи содержится уже в двухмерной ситуации. Если она работает в двух измерениях, ее можно перенести и на три измерения. Для этого требуется только немного уверенности.