
Доказательства теорем
1. Достаточно заметить, что а = а×1
2. По условию, найдутся такие d1 и d2 что а = bd1 и b = cd2. Но тогда а = cd1d2, т. е. а с.
с.
3. Мы имеем а = bc1 и b = ас2, откуда следует, что а = ас1с2, т. е. c1c2 = 1. Так как числа с1 и с2 по условию целые, то либо c1 = с2 = 1, либо c1 = с2 = -1. В первом из этих случаев а = b, а во втором а = -b.
4. Пусть а = bс. Если |c| ≥ 1, то поскольку |b| > |а|, должно быть и |bc| > |a|, что, однако, противоречит предположенному. Значит, |с| < 1, а так как по условию число с целое, должно быть c = О, а потому и а = 0.
5. Очевидно, из а = bс следует |а| = |b||с|, а из |a| = |b||c| следует а = bс или а = b(-с), причем числа с, -с и |с| целые или нет одновременно.
6. В самом деле, пусть
а1 = bc1,
а2 = bс2,
......
an = bcn,
где все числа с1, с2, ..., сn - целые. Сложив все эти равенства почленно, мы получим
a1 + а2 + .. аn = b(с1 + с2 + ... + сn).
В скобках стоит целое число, что и доказывает требуемое.
8. Доказательство ведется от противного. Предположим, что простых чисел конечное число, так что все они могут быть выписаны:
p1, p2, p3,....., pn (Д.1)
Произведение всех этих чисел обозначим через Р и рассмотрим разность Р - 1. Эта разность больше каждого из простых чисел, перечисленных в списке (Д.1), и потому не может быть простым числом. Следовательно, она делится хотя бы на одно простое число pk. Но Р также делится на pk. Следовательно, на основании следствия теоремы 6, должно быть и 1 pk, откуда следует, что pk = 1, а это противоречит простоте числа pk (см. стр. 21).
pk, откуда следует, что pk = 1, а это противоречит простоте числа pk (см. стр. 21).
Приведенное доказательство бесконечности множества простых чисел было найдено Евклидом (IV век до н. э.).
9. Если числа аир взаимно просты, то теорема доказана. Если же эти числа не взаимно просты, то оба они делятся на одно и то же число, отличное от единицы. Ввиду простоты р таким числом может быть только само р. Значит, в этом случае a  p, а это и требовалось.
p, а это и требовалось.
10. Разделив М на m с остатком, получим
М = mq + r,
где 0 г <т. Так как Мит делятся на а и Ь, по следствию теоремы б, число г также должно делиться и на а, и на Ь и тем самым быть общим кратным этих чисел. Но г ><т, а т есть наименьшее положительное общее кратное а и Ь. Значит, г не может являться положительным числом, так что г =. 0. Поэтому М; т.
>11. Пусть числа а и b взаимно просты, и m - их наименьшее общее кратное. Так как ab a и ab
a и ab b по предыдущей теореме ab
b по предыдущей теореме ab m. Пусть ab = mk. Положим m = ас. Тогда ab - ack, т. е. b = ck, так что b
m. Пусть ab = mk. Положим m = ас. Тогда ab - ack, т. е. b = ck, так что b k. Точно так же убеждаемся в том, что и а
k. Точно так же убеждаемся в том, что и а k Так как числа а и b по условию взаимно простые, должно быть k = 1, а это и означает, что m = ab.
k Так как числа а и b по условию взаимно простые, должно быть k = 1, а это и означает, что m = ab.
12. Обозначим через m наименьшее общее кратное чисел b и с. По предыдущей теореме m = bс. Далее, по условию ab с, кроме того, очевидно, аb
с, кроме того, очевидно, аb b. Значит, по теореме 10, ab
b. Значит, по теореме 10, ab bc, т. е. ab = bck или, после сокращения на b, а = ck, а это и требовалось.
bc, т. е. ab = bck или, после сокращения на b, а = ck, а это и требовалось.
13. Доказательство ведется индукцией по числу сомножителей. Если сомножитель один, то теорема тривиальна. Предположим, что теорема доказана для любого произведения n сомножителей. Пусть (a1a2...anan+1 p. Обозначим a1a2....an через А. Тогда Аan+1
p. Обозначим a1a2....an через А. Тогда Аan+1 p. Если an+1
p. Если an+1 p, то теорема доказана, а если нет, то по теореме 9 числа аn+1 и р взаимно просты. Но тогда по предыдущему А
p, то теорема доказана, а если нет, то по теореме 9 числа аn+1 и р взаимно просты. Но тогда по предыдущему А р. Так как А есть произведение n сомножителей, по индуктивному предположению один из них должен делиться на р. Теорема доказана.
р. Так как А есть произведение n сомножителей, по индуктивному предположению один из них должен делиться на р. Теорема доказана.
Следствие. Вся дробь представляет собой целое число, т. е. ее числитель делится на знаменатель. Будем считать, что числитель является произведением двух сомножителей: р и 1⋅2 ... (р - 1 ) = (р-1)!
Ни один из сомножителей знаменателя дроби не делится на р. Следовательно, по предыдущей теореме, на р не делится и весь знаменатель. Но тогда на основании теоремы 9 он взаимно прост с р. Поэтому на знаменатель должен делиться второй сомножитель числителя. Обозначая частное от этого деления через q, мы имеем Сkр = pq, и требуемое доказано.
14. Сначала докажем возможность разложения любого числа, отличного от единицы, на простые множители. Предположим, что все числа, меньшие N, могут быть так разложены. Если число N простое, то оно автоматически разлагается в произведение простых (именно, в произведение, состоящее только из одного сомножителя - самого числа N), и теорема доказана. Пусть теперь N составное, N1- некоторый делитель N, отличный как от N, так и от единицы, и N2 - частное от деления N на N1. Тогда N = N1N2, причем, как легко проверить, 1 < N2 < N. Так как N1 и N2 меньше N, то, по предположению, они разлагаются в произведения простых множителей. Пусть N1 = p1p2 ... pk и N2 = q1q2 ... ql - эти разложения. Тогда р1р2 ... pkq1q2 ... ql является искомым разложением числа N. Возможность разложения, таким образом, доказана.
Переходим к доказательству единственности разложения. Пусть нам даны два разложения числам на простые множители: р1р2 ... pk и q1q2 ... ql. Очевидно,
p1p2....pk = q1q2....ql (Д.2)
Так как q1q2 ... ql делится на р1 то по предыдущей теореме хотя бы одно из чисел q1, q2,....., ql делится на р1. Пусть q1 р1 (то, что мы считаем именно первый сомножитель в (Д.2) справа делящимся на р1 никакого дополнительного предположения не означает, так как мы вправе переставлять сомножители местами и обозначить через q1 именно тот из них, который делится на р1). Так как число q1 простое, это возможно лишь при р1 - q1. Сокращая равенство (Д.2) на р1 получаем
р1 (то, что мы считаем именно первый сомножитель в (Д.2) справа делящимся на р1 никакого дополнительного предположения не означает, так как мы вправе переставлять сомножители местами и обозначить через q1 именно тот из них, который делится на р1). Так как число q1 простое, это возможно лишь при р1 - q1. Сокращая равенство (Д.2) на р1 получаем
p1p2....pk = q1q2....ql (Д.3)
Аналогично предыдущему убеждаемся в том, что не которое из чисел q2, q3,...,ql (например, q2) делится на р2, и потому р2 = q2. Сокращая равенство (Д.З) на р2, мы уменьшаем число сомножителей в его частях еще на единицу. Такой процесс сокращения, очевидно, можно продолжать до тех пор, пока мы не сократим одно из произведений полностью. Пусть первым сократится произведение, состоящее в (Д.2) слева. Произведение, стоящее в (Д.2) справа, тоже должно при этом сократиться нацело, так как в противном случае мы получили бы равенство вида
1 = qk+1....ql
которое невозможно, так как единица не делится ни на какое простое число. При этом мы получаем также, что
p1 = q1, p2 = q2, ...., pk = qk
Теорема полностью доказана.
15. Пусть

и
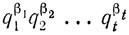
соответственно канонические разложения чисел а и b, a d - некоторый общий делитель этих чисел. Если d ≠ 1, то d делится на некоторое простое число р. Тогда по теореме 3 а  р и b
р и b р, так что р находится как среди чисел р1, р2, ...., pk, так и среди чисел q1, q2, ..., ql. Поэтому среди простых чисел, входящих в каноническое разложение а, существует хотя бы одно, входящее в каноническое разложение b.
р, так что р находится как среди чисел р1, р2, ...., pk, так и среди чисел q1, q2, ..., ql. Поэтому среди простых чисел, входящих в каноническое разложение а, существует хотя бы одно, входящее в каноническое разложение b.
Наоборот, если а и b взаимно просты и р входит в каноническое разложение а, то b не делится на р, так что р не может входить в каноническое разложение b.
16. Необходимость. Так как
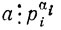
(i = 1, 2, ..., k), мы из b  a получаем требуемое простой ссылкой на теорему 2.
a получаем требуемое простой ссылкой на теорему 2.
Достаточность доказывается по индукции. Делимость b  p1α1 мы имеем в числе условий. Предположим, что нами уже установлено, что
p1α1 мы имеем в числе условий. Предположим, что нами уже установлено, что
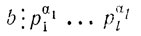
( 1 ≤ l < k)
Кроме того, в нашем распоряжении имеется делимость b pαl+1l+1 . Так как числа pα11.....pαll и pαl+1l+1 по предыдущей теореме взаимно просты, мы можем применить следствие теоремы 11, которое дает нам
pαl+1l+1 . Так как числа pα11.....pαll и pαl+1l+1 по предыдущей теореме взаимно просты, мы можем применить следствие теоремы 11, которое дает нам
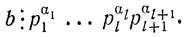
Этим индуктивный переход обоснован.
17. Необходимость. Пусть а  b. Из теоремы 13 следует, что каждый простой делитель b является простым делителем а. Таким образом, b имеет вид
b. Из теоремы 13 следует, что каждый простой делитель b является простым делителем а. Таким образом, b имеет вид
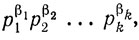
где 0 ≤ β1, 0 ≤ 2, ...., 0 ≤ k. Предположим, что β1 > α1. Так как
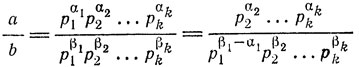
- целое число, числитель последней дроби должен делиться на знаменатель и тем более на число р1β1-α1. Но тогда по теореме 13 на р1 должно делиться хотя бы одно из чисел р2, ..., pk, чего не может быть. Значит, β1 ≤ α1. Так как нумерация простых делителей а для нас безразлична, мы тем самым доказали, что и β2 ≤ α2,...., βk ≤ αk. Необходимость доказана.
Для доказательства достаточности заметим, что если b имеет указанный вид, то
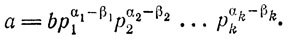
18. Напишем канонические разложения чисел m
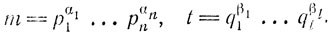
Отберем среди простых р1,...,pn те, которые делят t, т. е. содержатся среди q1,....,ql. Пусть для определенности это будут p1,...,pr равные соответственно числам q1,.....,qr. Положим тогда
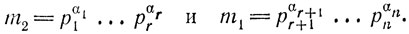
Согласно теореме 15 будет (m1,t) = 1. Кроме того, возьмем натуральное число k, которое было бы не меньше каждого из отношений
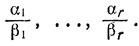
Это значит, что kβi ≥ αi для i = 1,...., r, откуда согласно теореме 17 tk m2.
m2.
19. Необходимость. Пусть
a = mq1 + r1 (0 ≤ r1 <m) (Д.4)
a = mq2 + r2 (0 ≤ r2 <m) (Д.5)
Ввиду равно-остаточности a и b должно быть r1 = r2.
Значит,
a - b = m(q1 - q2),
т. е. (а - b) m.
m.
Достаточность. Пусть (а - b) m. Разделов a и b на m с остатком, мы получим (Д.4) и (Д.5). При этом
m. Разделов a и b на m с остатком, мы получим (Д.4) и (Д.5). При этом
а - b - m(q1 - q2) + r1 - r2
т. е.
(a - b) - m (q1 - q2) = r1 - r2.
По теореме 6 (r1 - r2) m. Но |r1 - r2| < m. Значит, по теореме 4 r1 - r2 = 0 или r1 = r2, а это и требовалось.
m. Но |r1 - r2| < m. Значит, по теореме 4 r1 - r2 = 0 или r1 = r2, а это и требовалось.
20. Из условия на основании теоремы 16 мы имеем
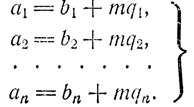
Сложив почленно эти равенства, мы после простых преобразований получаем
(a1 + а2 + ... + аn) - (b1 + b2 + ... + bn) = m (q1 + q2 + ... + qn)
что по теореме 19 и означает равно-остаточность сумм.
Для доказательства равно-остаточности произведений отметим следующее тождество:
(k + bm)(р + qm) - kp + (pq + lp + lqm)m.
Из него следует, что произведение двух чисел вида а + bm снова является числом того же вида. Поэтому, рассуждая по индукции, мы убеждаемся в том, что произведение любого количества чисел вида а + bm есть число этого же вида.
Перемножив теперь почленно все равенства (Д.6) и применив к правой части только что проведенные рассуждения, мы получаем
a1a2....an = b1b2 .... bn + mt,
где t - некоторое целое число. Равно-остаточность произведений, таким образом, доказана.
21. Необходимость. Если описанный алгорифм является признаком равно-остаточности при делении на т, то числа А и b при делении на m должны быть равно-остаточными. В частности, это будет так, если A = tk + b. Но это значит, что A - b = tk m.
m.
Достаточность. В наших обозначениях A - b = atk, т. е. числа А и b равно-остаточны при делении на m. Если tk m, то по следствию теоремы 17 они равно-остаточны и при делении на m. Поэтому конструируемая алгорифмом в этом случае последовательность A0, A1 ... состоит из равно-остаточных при делении на m чисел. Следовательно, процесс построения этой последовательности является признаком равно-остаточности при делении на m.
m, то по следствию теоремы 17 они равно-остаточны и при делении на m. Поэтому конструируемая алгорифмом в этом случае последовательность A0, A1 ... состоит из равно-остаточных при делении на m чисел. Следовательно, процесс построения этой последовательности является признаком равно-остаточности при делении на m.
22. Необходимость. Если описанный алгорифм действительно является признаком равно-остаточности при делении на m, то он, в частности, должен быть применим и к числу A = tk + а0. Здесь f(A) = а0 + 1, и равно-остаточность чисел A и f(A) при делении на m означает (tk - 1) m.
m.
Достаточность. Пусть А ≥ tk. Тогда из определения функции f следует, что
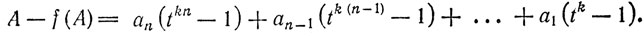
Здесь каждое слагаемое (см., например, задачу 22, п. д)) делится на tk - 1. Значит, если (tk- 1) m, то и (А - f(A))
m, то и (А - f(A)) m. Равно-остаточность остальных членов последовательности (3.4), а также ее членов, если она начинается с числа А < tk, вытекает из ее построения.
m. Равно-остаточность остальных членов последовательности (3.4), а также ее членов, если она начинается с числа А < tk, вытекает из ее построения.
23. Необходимость. В случае А = tk + a0 равно-остаточность чисел А и f(A)= a0 - 1 при делении на m дает нам (tk + 1) m.
m.
Достаточность. Мы имеем в нашем случае при А ≥ tk
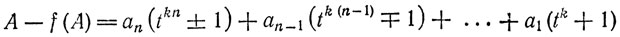
(знак "плюс" стоит здесь в члене, соответствующем нечетному коэффициенту при k в показателе, а знак "минус" - в члене, соответствующем четному коэффициенту). Согласно пп. д) и е) задачи 22 при нечетном r выражение tkr + 1 делится на tk + 1, а при четном r выражение tkr - 1 делится на tk - 1. Значит, если (tk - 1) m, то на m делится каждый член в (Д.7) справа, а потому и вся разность А - f(A). Тем самым числа А и f(A) оказываются равно-остаточными при делении на т. Равно-остаточность остальных членов последовательности (3.4), а также членов этой последовательности, если она начинается с числа А < tk, вытекает непосредственно из ее построения.
m, то на m делится каждый член в (Д.7) справа, а потому и вся разность А - f(A). Тем самым числа А и f(A) оказываются равно-остаточными при делении на т. Равно-остаточность остальных членов последовательности (3.4), а также членов этой последовательности, если она начинается с числа А < tk, вытекает непосредственно из ее построения.
24. Доказательство ведется индукцией по а. При а = 1 имеем
ар - а = 1 - 1 = 0
и 0 р.
р.
Предположим, что ар - а делится на р, и докажем, что (а+1)р - (а+1) также делится на р.
Действительно, разлагая (а + 1)р по формуле бинома Ньютона, имеем
(а + 1)р - (а + 1) = ар + С1pap-1 + C2pap-2+...+Cpp-1a + 1 - a - 1 = ap - a + C1pap-1 + C2pap-2 + ....+ Cpp-1a. (Д-8)
ар - а делится на р по предположению. По следствию теоремы 13 Ckp (при 1 ≤ k ≤ р - 1) также делится на р. Следовательно, на р делится каждое слагаемое правой части соотношения (Д.8), а потому (теорема 6) и вся сумма.
Индуктивный переход обоснован, и вся теорема доказана.
Следствие. По теореме Ферма
ар - а = а(ар-1 - 1 ) р.
р.
 р.
р.Если при этом а не делится на р, то по теореме 13 на р должно делиться ар-1 - 1.
25. Пусть
m1 = p1α1... pkαk и m2 = q1β1 ... qlβl
По теореме 15 каждое из чисел р1 ..., pk отлично от каждого из чисел q1, ..., ql Значит, каноническим
разложением m1m2 будет p1α1....pkαkq1β1.......qlβl. Поэтому
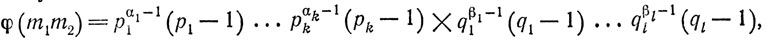
т. е.
φ(m1m2) = φ(m1)φ(m2).
26. Докажем сначала индукцией по α, что аpα-1(p-1) - 1 делится на рα. При α = 1 доказываемое утверждение является, очевидно, следствием теоремы Ферма, справедливость которого уже была установлена. Таким образом, основание индукции доказано.
Предположим теперь, что
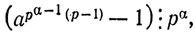
и рассмотрим выражение
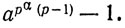
Мы должны доказать, что оно делится на рα+1. Но
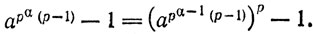
Так как аpα-1(p-1) - 1, по предположению, делится на рα, число аpα-1(p-1) имеет вид Npα + 1. Значит,
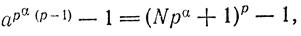
т. е. по формуле бинома
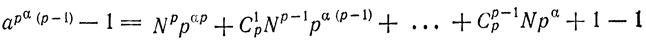
В последней сумме первое слагаемое делится на pα+1, так как оно делится на рαp и αр ≥ α + 1. В каждое из следующих р - 1 слагаемых этой суммы входит р с показателем, не меньшим α, и, кроме того, биномиальный коэффициент, в силу следствия теоремы 13 делящийся на р. Значит, каждое из этих слагаемые также делится на pα+1. Наконец, разность 1 - 1 = 0 может быть отброшена. Поэтому по теореме 6
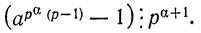
Случай, когда число m имеет только один простой делитель, таким образом, разобран.
Предположим теперь, что теорема Эйлера доказана для показателей m1 и m2, причем числа m1 и m2 взаимно простые. Докажем теорему Эйлера для показателя m = m1m2. Если потом положить
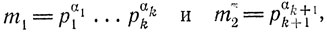
то мы, очевидно, и получим индуктивный переход, необходимый нам для завершения доказательства теоремы. Итак, доказываем высказанное утверждение.
Пусть числа а и m взаимно просты. Тогда а также взаимно просто с m1. Значит, и aφ(m2) взаимно просто с m1. Поэтому, по предположению,
(aφ(m2))φ(m1) - 1 = aφ(m1)φ(m2) - 1 = aφ(m1m2) - 1 = aφ(m) - 1
делится на m1. Точно так же убеждаемся в том, что aφ(m) - 1 делится и на m2. А так как числа m1 и m2 взаимно простые, аφ(m) - 1 делится и на их произведение, т. е. на m. Теорема Эйлера доказана.
27. Пусть
k1 = φ(m)q1 + r,
k2 = φ(m)q2 + r.
Тогда
ak1 = аφ(m)q1+r = (aφ(m))q1ar
На основании теоремы Эйлера и теоремы 20 число aφ(m)q1ar равно-остаточно при делении на m с числом ar. Аналогично устанавливается равноостаточность при этом делении чисел ak2 и ar. Значит, и числа ak1 и аk2 при делении на m равно-остаточны.
28. Найдем сначала хотя бы одно решение (х',y') этого уравнения. Очевидно, что для этого достаточно найти такое число х', что (ах' - с) b. По теореме Эйлера (аφ(b)-1)
b. По теореме Эйлера (аφ(b)-1) b. Значит, (саφ(b) - с)
b. Значит, (саφ(b) - с) b, и в качестве х' можно взять число сaφ(b)-1
b, и в качестве х' можно взять число сaφ(b)-1
Пусть теперь (x",y")-какое-то другое решение уравнения ах + by - с. Покажем, что числа х' и х" равно-остаточны при делении на b. В самом деле, пусть
ах' + by' = с,
ах" + by" - с.
Вычитая почленно второе равенство из первого, получаем
а(х' - х") - b(y' - y") = 0,
откуда а(х' - х") b. Так как а и b по условию взаимно просты, по теореме 12 (х' - х")
b. Так как а и b по условию взаимно просты, по теореме 12 (х' - х") b, и нам остается сослаться на теорему 19.
b, и нам остается сослаться на теорему 19.
Таким образом, все искомые значения х находятся среди чисел
xt = caφ(b)-1 + bt
Но (axt - с) b, так что, полагая
b, так что, полагая
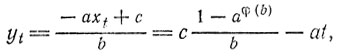
мы получаем, что все пары чисел xt и yt являются решениями нашего уравнения.
29. Ввиду взаимной простоты m и 10, числа 10а + b и (10а + b) по теореме 15 равноделимы на m. Но
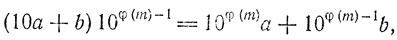
так что по теореме Эйлера и теореме 20 число 10a + b равноделимо на m с числом a + kb.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'