Решения задач

1. 0 = а × 0 при любом а.

2. а = 1 × а, значит, а 1.

3. Пусть 1 а. Это значит, что 1 = ас при некотором целом с. Отсюда следует, что |а|≤1. А так как а ≠ 0, должно быть а = 1.

4. Достаточно взять любое с > 1 и положить b = ас.

5. В качестве такого b можно взять, например, 2а, Пусть при этом для некоторого с и 2а с и с а. Это значит, что найдутся такие d₁ и d₂, что 2а = d₁c и с = d₂a. Отсюда следует, что 2а = d₁d₂a или, после сокращения на а,

Но при целых d₁ и d₂ такое равенство возможно лишь в случае, когда одно из этих чисел равно 1, а другое 2. Если d₁ = 1, то с = 2а = b; если же d₁ = 1, то с = а.

6. Доказательства ничем не отличаются от доказательств в случае обычной делимости.

7. Пусть n - некоторое фиксированное число, большее единицы. Положим а _n b, если найдется такое целое с, что а = bc и c ≤ n. Справедливость теорем, аналогичных теоремам 1, 3 и 4, проверяется без труда. Однако если мы возьмем а = nb и b = nc, то а _n b и b _n с. В этом случае а = n²с, а так как n² > n, делимость а _n с не имеет места. Точно также не имеет места делимость (а + а) _n b.

8. а) Пусть имеются два минимальных числа a₁ и a₂. В силу дихотомичности либо a₁ ≥ а₂, либо а₂ ≥ а₁. Если a₁ ≥ а₂, то из минимальности a₁ следует, что a₁ = а₂. Вели же а₂ ≥ a₁, то a₁ = а₂ следует из минимальности а₂.

б) Пусть а - некоторое число, a b₁ и b₂ - два непосредственно предшествующих ему числа. По дихотомичности должно быть либо b₁ ≥ b₂, либо b₂ b₁. Пусть, для определенности, b₁ ≥ b₂. Мы имеем a ≥ b₁ ≥ b₂, а так как число b₂ непосредственно предшествует числу а, должно быть либо b₁ = а, либо b₁= b₂. Но по условию b₁ ≠ а; значит, b₁ = b₂, и требуемая единственность доказана.

в) Непосредственно следующим за а числом называется такое b, что b ≥ а, b ≠ а, и из b ≥ с ≥а следует либо c = b, либо с = а.

Предположим, что некоторое а не имеет непосредственно следующего за ним числа. Это значит, что для любого а_n ≥ а и отличного от а найдется такое а_n+1 отличное как от а_n, так и от а, что а_n ≥ а_n+1 ≥ а. Возьмем теперь произвольное a₁ ≥ а и отличное от а (в силу 2° это сделать можно) и, исходя из него, построим бесконечную последовательность различных чисел

Существование же этой последовательности противоречит 4°. Следовательно, непосредственно следующее число существует. Единственность его устанавливается при помощи дихогомичности подобно тому как это делалось в пп. а) и б).

9. Остается в силе транзитивность (3°), неограниченность множества чисел (5°), свойство 4° и существование непосредственно предшествующего числа (6°). Дихотомичность заменяется трихотомичностыо (либо a > b, либо b > а, либо а = b).

Становится неверным свойство рефлексивности (1°), ибо а > а всегда неверно.

Что же касается, наконец, утверждения 2°, то формально оно остается в силе (хотя, быть может, и выглядит несколько Парадоксально).

В самом деле, говоря строго, это утверждение в нашем случае формулируется так: для любых натуральных чисел а и b из а > b и b > а следует а = b.

Предположим, что это высказывание неверно. Тогда найдутся такие натуральные числа а и b, что одновременно будет и а > b и b > а, и а ≠ b, а этого не может быть. Полученное противоречие доказывает истинность нашего утверждения.

10. Пусть множество упорядочено отношением 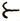обладающим свойствами 1 - 7°. Как уже было установлено, оно обладает минимальным элементом. Обозначим этот элемент через а₀. Из результатов задачи 8 следует, что каждый элемент обладает непосредственно следующим. Обозначим непосредственно следующий за а₀ элемент через a₁, непосредственно следующий за a₁ - через a₂ и т. д. В итоге мы получаем последовательность

в которой а_n+1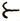a_n при любом n. По рефлексивности и транзитивности отношения 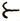отсюда следует, что a_i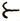a_j тогда и только тогда, когда i ≥ j. Нам остается показать, что последовательность (Р.1) охватывает все рассматриваемые нами объекты. Это достигается довольно тонким рассуждением по индукции.

Предположим, что b₀ не принадлежит последовательности (Р.1). Получение этого b₀ будем считать первым шагом нашего индуктивного рассуждения. Пусть n его шагов уже проведены, в результате чего нами получен некоторый элемент b_n-1.

Если b_n-1 = а₀, то наш процесс будем считать законченным; если же b_n-1 ≠ a₀, то элемент b_n-1 имеет непосредственно пред-шествующий, который мы и возьмем в качестве b_n. В результате получаем последовательность различных элементов

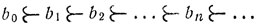
На основании 4° эта последовательность должна иметь последний член. Но по самому принципу построения этой последовательности ее последним членом может быть только а₀. Пусть для определенности b_n = a₀.

Нетрудно проверить, что если некоторое а непосредственно предшествует b, то b непосредственно следует за а. Значит, b_n-1 = a₁, b_n-1 a₁, b_n-2 = a₂, . . .,b₀ = a_n.

Последнее означает, что b₀ принадлежит последовательности (Р.1), но это противоречит предположенному. Следовательно, последовательность (Р.1) содержит все рассматриваемые нами объекты.

11. Пусть а - некоторое число. Всякую последовательность различных чисел а₀ = a, a₁, а₂, . .. , а_n, для которых

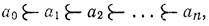
где a_n минимально в смысле упорядочения 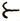, назовем цепью Предшественников а₀. Число n называется длиной этой цепи.

Покажем сначала, что при тех условиях, которые мы наложили на упорядочение 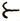, каждое конкретное число не может иметь сколь угодно длинных цепей предшественников.

В самом деле, пусть а - некоторое число, a b₁, b₂, ..., b_k - непосредственно предшествующие ему числа.

Если a₁ не предшествует a₀ непосредственно, мы можем на основании 9° вставить в цепь (Р.2) некоторое непосредственно предшествующее а число. Поэтому если имеются сколь угодно Длинные цепи предшественников а, должны найтись и такие его сколь угодно длинные цепи предшественников, которые начинаются с чисел, непосредственно предшествующих а. Будем далее рассматривать только такие цепи.

Каждая цепь предшественников а ровно на единицу длиннее некоторой цепи предшественников одного из непосредственно Предшествующих ему чисел. Если бы каждое из них имело цепи предшественников ограниченной длины, то само а не могло бы иметь сколь угодно длинных цепей предшественников.

Значит, при нашем предположении хотя бы одно из чисел, непосредственно предшествующих а₀, имеет сколь угодно длинные цепи предшественников. Обозначим это число через а₁ и повторим в применении к нему все только что проведенные рассуждения. Это даст нам некоторое число а₂, непосредственно предшествующее а₁ и имеющее сколь угодно длинные цепи предшественников. Повторяя этот процесс, мы приходим к последовательности

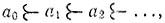
которая в силу 4° должна рано или поздно оборваться. Это значит, что последовательность будет иметь такой член, к которому наши рассуждения уже будут неприменимы. Но применимость рассуждений к каждому последующему члену последовательности нами уже была установлена. Полученное противоречив показывает, что ни одно число не имеет сколь угодно длинных цепей предшественников.

Следовательно, для каждого числа а среди его цепей предшественников можно выбрать самую длинную. Обозначим ее длину через n(а). Если b непосредственно предшествует а, ТО очевидно, n(b) = n(а)-1, а для всех минимальных a n(a) = 0.

Пусть, наконец, А (а)-высказывание, зависящее от а. Обозначим через В(n) высказывание "A(а) верно для всех чисел а, для которых n(а) = n". Тогда, как легко видеть, формулировка принципа индукции в новой форме для утверждений А (а) совпадает с формулировкой этого принципа в старой форме для утверждений В(n).

12. Каковы бы ни были четные числа а и b, существуют такие четные числа q и r, что

Такие числа q и r единственны.

Доказательство. Разделим а на 26 с остатком обычным образом:

При этом числа q и r определяются однозначно. Из четности и 2bq следует четность их разности, т. е. числа r. Нам остается, положив 2q = q', переписать (Р.3) в виде

и заметить, что оба числа q' и r четные и определяются единственным образом.

13. Пусть р - наименьший простой делитель числа а. Отсюда следует, что а = pb. Всякий простой делитель q числа b является вместе с тем и делителем а. Поэтому q ≥ р, значит, и b ≥ р, так что а ≥ р² и, наконец, р ≤ √а .

14. Пусть р₁, р₂,..., p_k - полный список всех простых чисел, входящих хотя бы в одно из канонических разложений а и b. Положим

(Если а не делится на р_i, то α_i = 0; если b не делится на p_i, то β_i = 0.) Пусть γ_i - наибольшее из чисел α_i и β_i для t = 1, 2, ..., k, а δ_i - наименьшее из них.

Тогда, на основании теоремы 17, наибольший общий делитель а и b есть p₁^δ₁p₂^δ₂....p_k^δ_k а их наименьшее общее кратное - p₁^γ₁p₂^γ₂....p_k^γ_k.

15. Как следует из теоремы 17, каждый делитель числа а с каноническим разложением p₁^α₁p₂^α₂....p_k^α_k должен иметь вид p₁^β₁p₂^β₂...p_k^β_k, где β₁ принимает α₁ + 1 значений: 0, 1, 2, ..., α₁, β₂ принимает α₂ + 1 значений и т. д. Так как любые комбинации этих значений возможны и дают нам все делители а, причем; каждый по одному разу (если бы какой-нибудь делитель повторился несколько раз, то это означало бы наличие у него нескольких канонических разложений), число делителей а равно

16. Пусть каноническое разложение а есть p₁^α₁p₂^α₂....p_k^α_k. Очевидно, можно положить p₁ = 2, α₁ ≥ 2 и р₂ = 3, α₂ ≥ 1. Далее, согласно (Р.4), мы имеем

Отсюда k = 2, α₁ + 1 = 7 и α₂ + 1 = 2. Таким образом, α = 2⁶×3 = 192.

17. Мы имеем

так что (2α₁ + 1) (2α₂ + 1) есть разложение числа 81 на два множителя. Так как нумерация простых делителей а зависит от нас, ограничимся рассмотрением следующих возможностей:

В первом из этих случаев α₁ = 0, что противоречит предположенной положительности числа α₁. Оставшиеся случаи дают там

Значит, либо

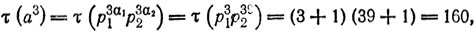
либо

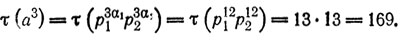
18. Пусть p₁^α₁p₂^α₂....p_k^α_k - каноническое разложение числа а. Условие задачи дает нам

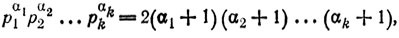
или

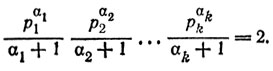
Заметим, что

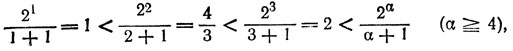
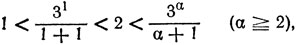
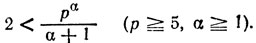
Поэтому в (Р.5) слева каждая дробь не меньше единицы и, следовательно, ни одна из дробей не может быть больше, чем 2. Значит, в левой части (Р.5) могут стоять лишь дроби из следующего набора:

причем их произведение есть 2. Но это может быть лишь в двух случаях: когда в (Р.5) слева стоит только одна дробь 2³/(3+1) или когда там стоят две дроби 2²/(2+1), 3¹/(1+1).Этим двум случаям соответствуют два ответа задачи: 8 и 12.

19. Напишем каноническое разложение числа а:

Тогда

и согласно (Р.4) (задача 15)

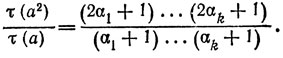
Легко видеть, что каждая дробь (2α_i + 1)/(α_i + 1) с ростом α_i возрастает (приближаясь к 2), так что наименьшее значение этой дроби будет достигаться при α_i = 1 и будет равно 3/2. Это значит, что

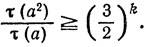
Ясно, что при достаточно большом k будет (3/2) > K. Для этого достаточно взять

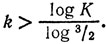
Например, при K = 100 достаточно взять k > 2/0,18 == 11,1; так как число k должно быть целым, можно взять k = 12.

20. Аналоги теорем 11-14 для четной делимости неверны. В самом деле, числа 30 и 42 четно простые. Их наименьшее четное кратное есть 420, а произведение - 1260.

Далее, 60 = 6×10 четно делится на четно простое число 30; 6 и 30 четно взаимно просты, а 10 четно на 30 не делится.

Наконец, 60 = 6 × 10 = 30×2 - два различных разложения числа 60 на четно простые множители.

21. а) 116 при делении на 8 равноостаточно с 4, а 17 - с 1. Значит, А равноостаточно с 5²¹ = (5²)¹⁰×5. Но 5² = 25 при делении на 8 равноостаточно с единицей. Следовательно, А при делении на 8 дает в остатке 5.

б) 14 при делении на 17 равноостаточно с -3. Поэтому А равноостаточно с (-3 )²⁵⁶ = 3²⁵⁶ = (3³)⁸⁵×3. Но 3³ мы можем заменить на 10: 10⁸⁵×3 = (10²)⁴²×30. Далее, 10² при делении на 17 равноостаточно с числом -2, а 2⁴ с -1. Значит, А равноостаточно с (-2)⁴²×30 = 2⁴²×30 = (2⁴)¹⁰×4×30 = (-1)¹⁰×4×30 = 120. Последнее же число при делении на 17 дает в остатке 1.

22. а) Пусть n₁ - остаток от деления n на 6. Тогда n₁ может принимать значения 0, 1, 2, 3, 4 и 5, а n³₁ + 11n₁ при делении на 6 равноостаточно с n³ + 11n. Значит, нам следует испытывать делимость на 6 чисел 0, 12, 30, 60, 108 и 180. Но все эти числа на 6 делятся.

Для получения того же результата можно воспользоваться и более частными соображениями. Число n³ + 11n равноостаточно при делении на 6 с числом n³ + 11n - 12n = n³ - n = (n - 1)n(n + 1). Но из трех последовательных целых чисел n - 1, n и n + 1 хотя бы одно - четное (т. е. делится на 2) и ровно одно делится на 3. Значит (согласно следствию теоремы 11), произведение этих трех чисел делится на 6. Кстати, можно заметить, что

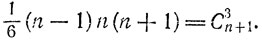
б) При n ≥ 2 мы имеем (пользуясь формулой бинома)

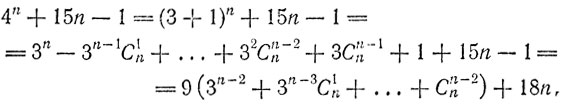
и оба слагаемых, очевидно, делятся на 9.

При n = 1 наше выражение равно 4¹ + 15×1 - 1 = 18.

в) Доказательство ведется по индукции.

При n = О

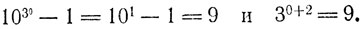
Пусть теперь делимость

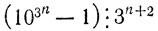
имеет место. Тогда

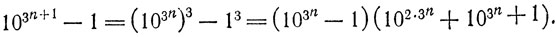
Первый сомножитель справа делится на 3ⁿ⁺² по индуктивному предположению. Во втором же сомножителе мы можем заменить десятки на равноостаточные им при делении на 3 единицы; полученное число 3 показывает, что второй сомножитель делится на 3. Следовательно, все произведение делится на 3ⁿ⁺³ = 3^(n+1)+2 что и требовалось.

г). При делении на а²- а + 1, очевидно, а² равноостаточно с а - 1. Значит,

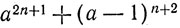
равно-остаточно с

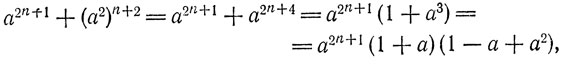
что и требовалось.

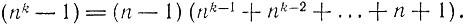
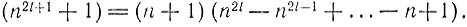
23. Пусть ~ - эквивалентное отношение на множестве чисел. Возьмем произвольное число а и рассмотрим все числа, эквивалентные а. Все они ввиду транзитивности отношения ~ эквивалентны между собой. Обозначим через К класс всех этих чисел.

Рассмотрим теперь произвольное число b, не принадлежащее К? Если бы было b ~ с, где с - некоторое число из К, то было бы и b ~ а, чего, однако, не может быть по выбору b. Значит, ни одно из чисел, лежащих вне К, не эквивалентно ни одному из чисел К. Следовательно, К есть класс эквивалентности, содержащий а.

Так как число а было нами взято совершенно произвольно, проведенные рассуждения показывают, что каждое число принадлежит некоторому классу эквивалентности. Это и требовалось.

24. Очевидно, среди чисел 0, 1, ..., m найдутся два, принадлежащие одному классу. Пусть этими числами будут k и l k ~ l. Таких пар чисел из одного класса может оказаться, вообще говоря, и несколько. Выберем ту из них, для которой величина |k - l| будет наибольшей. Поскольку - l ~ - l, мы, по условию, получаем

Далее, мы находим, что и при любом целом n

Наконец, при любом r

т. е. из а ≡ b(mod k - l) следует а ~ b, Таким образом, классы отношения ~ содержат целиком классы вычетов по модулю m.

Для того чтобы классов ~ -эквивалентности было m, необходимо, чтобы каждый класс ~ -эквивалентности содержал не более одного класса вычетов и чтобы k - l = m.

25. а) Обе части сравнения и модуль можно разделить на одно и то же число (разумеется, отличное от нуля).

В самом деле,

означает, что

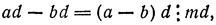
т. e.

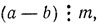
откуда a ≡ b (mod m).

б) Обе части сравнения можно разделить на число, взаимно простое с модулем.

Действительно, если d и m взаимно просты, то из

т. е. из

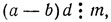
следует на основании теоремы 12, что (а - b) m, что и требовалось.

26. Предположим, что

Это значит, что (l - k)a р. Поскольку а не делится на р, должно быть (l - k) р. Но и этого не может быть, так как 0. < l - k < p.

27. Необходимость. Пусть число р простое. Возьмем 0 < q < р. Среди чисел q, 2q, ..., (p - 1)q найдется ровно одно, дающее при делении на р в остатке единицу. Пусть этим числом будет qq:

С другой стороны, среди чисел q, 2q, ..., (p - 1)q также может быть лишь одно, дающее при делении на р в остатке единицу. Это, как уже установлено, число qq.

Выясним, в каких случаях q = q. Во всех таких случаях сравнение (Р.6) переписывается так:

или, что то же самое,

Это значит, что

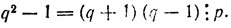
Ввиду того, что число р простое, по теореме 13 должно быть либо (q + 1) р, либо (q - 1) р. Так как число q заключено между нулем и р, первый из этих случаев возможен лишь при q = p - 1, а второй - при q = 1. Таким образом, при р = 2 и р = 3 всегда q = q, при р ≥ 5 - лишь в случаях q = 1 и q = p - 1.

Следовательно, при р ≥ 5 все оставшиеся числа 2, ..., р - 2 можно объединить в такие (р - 3)/2 пары, что произведение чисел, составляющих каждую из пар, при делении на р дает в остатке 1. Выпишем сравнения вида (Р.6) для всех таких пар, добавив в этот список сравнение

и перемножим все (р - 1)/2 полученных сравнений почленно.

В результате такого умножения мы получим слева произведение всех чисел от 2 до р - 1, а справа р - 1:

или

Последнее сравнение означает, что

а это и требовалось.

Остается проверить случаи р = 2 и р = 3. Но для них, очевидно, (1 + 1) 2 и (2 + 1) 3.

Достаточность. Если число р не простое, то оно может быть разложено в произведение двух меньших множителей: р = p₁р₂.

Если р₁ ≠ р₂, то и p₁ и р₂ входят сомножителями в произведение 1×2...(р - 1), которые тем самым делятся на р₁p₂, т.е. на р. Пусть теперь p₁ = р₂ = q. Тогда р = q² (т. е. р есть квадрат простого числа). Если q > 2, то p > 2q, и в произведение 1×2...(р - 1) входят множителями q и 2q, так что в этом случае оно делится на q², т. е. на р. В обоих случаях 1×2...(р - 1) + 1 на р делиться не может. Наконец, если р = 4, то 1×2×3 - 1 = 5, и на 4 не делится.

28. Теорема. Пусть m = р₁^α₁р₂^α₂ ... р_k^α_k - каноническое разложение m. Тогда для того чтобы числа А и В были равноостаточными при делении на m необходимо и достаточно, чтобы они были равноостаточными при делении на р₁^α₁ на р₂^α₂,...., на p_k^α_k.

Доказательство. Необходимость. Равноостаточность А и В при делении на m означает (А - В) m. Тем более (А - В) р_i^α_i (i = 1, ..., k), и числа А и В оказываются равноостаточными при делении на все р_i^α_i.

Достаточность. Пусть числа А и В при делении на а, каждое p_i^α_i равноостаточны. Обозначим через r_i остаток от деления А и В на р_i^α_i (i = 1, 2, ,. k). Это значит, что

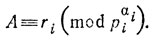
Положим, далее,

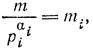
и умножим в сравнении (Р.7) обе части и модуль на m_i.

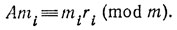
Сложив все такие сравнения почленно, мы получим

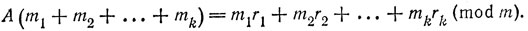
Ввиду равноостаточности A и В при делении на p₁^α₁, p₂^α₂,...,p_k^α_k мы получаем также

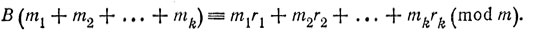
Вычтя почленно сравнение (P.9) из (P.8), мы имеем

т. е. (A - B) (m₁ + m₂ + ... + m_k) m.

Но сумма m₁ + m₂ + ... + m_k взаимно проста с m. В самом деле, если бы она имела с m некоторый общий простой делитель р, то он входил бы в каноническое разложение т, т. е. имел бы вид p_i. Но тогда на него делилась бы как вся сумма, так и каждое слагаемое, кроме одного, m_i, а этого быть не может.

Теперь мы можем применить теорему 12, которая даст, что (A - В) m, т. е. числа А и В при делении на m равноостаточны.

29. а) Выпишем систематически все равенства, описывающие деления с остатком, которые составляют применение алгорифма Евклида к числам а и b:

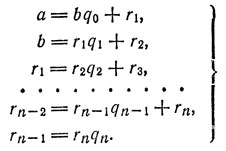
Мы имеем r_n-1 r_n. Вместе с r_n-2 = r_n-1q_n-1 + r_n, это дает нам r_n-1 r. Продвигаясь аналогичным образом вверх по системе равенств (Р. 10), мы получаем, наконец, что а r_n и b r_n, Значит, r_n есть общий делитель а и b.

Пусть d - любой общий делитель а и b. Вместе с а = bq₀ + r₁ это дает нам r₁ d. Продвигаясь по системе равенств (Р.10) вниз, мы будем последовательно получать, что r₂ d, r₃ d,..., r_n d. Значит, r_n делится на любой общий делитель а и b, являясь тем самым наибольшим общим делителем этих чисел.

б) Доказательство ведется по индукции. Полагая А₀ = 0, В₀ = 1, A₁ = 1, В₁ = -q₀, мы имеем r₀ - b = аА₀ + bВ₀ и r₁ = аА₁ + bВ₁.

Пусть теперь

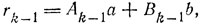
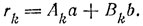
Но тогда

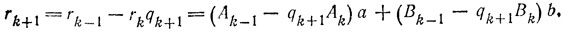
и нам остается положить

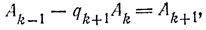
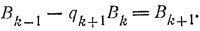
Числа A_n и B_n окажутся искомыми A и В.

30. Если бис взаимно просты, то по предыдущему можно найти такие целые В и С, что

или, после умножения на а,

ab с по условию; ас с очевидным образом; значит, и а с.

31. Ограничимся рассмотрением признака равно-остаточности при делении на 8.

Пусть произвольное натуральное А представлено в виде 1000а + b, где 0 ≤ b < 1000 (т. е. b - трехзначное число, которым оканчивается А), и

32. Ограничимся рассмотрением признака равно-остаточности при делении на 18 в двенадцатеричной системе счисления.

Пусть А представлено в виде 144а + b, где 0 ≤ b < 144 (т. е. b - двузначное в двенадцатеричной системе счисления число, которым оканчивается записанное в этой системе число A), и

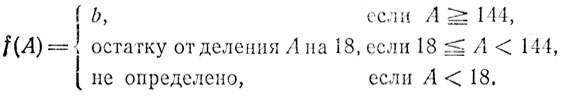
Проверка того, что процесс построения последовательности A, f(A), f(f(A)), ... действительно является признаком равноостаточности, осуществляется стандартно.

33. Для тех m, у которых каноническое разложение имеет вид 2^α×5^β.

34. Условия а) и б) выполняются автоматически. Поскольку при делении на 3 числа 10 и 1 равноостаточны, равноостаточными же должны быть и числа A и f(A). Наконец, то, что f(A) < A при А ≥ 3, устанавливается простым подсчетом.

35. а) f(858 773) = 38; f(38) = 11; f(11) = 2.

б) f(A) = 4444.4 = 17 776; f(17 776) = 28; f(28) = 10; f(10) = 1.

36. Признак равноостаточности при делении на 9 аналогичен рассмотренному признаку равноостаточности при делении на 3.

Для получения признака равноостаточности при делении на 11 представим число А в виде

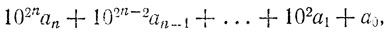
где 0 ≤ a_i < 100. Очевидно, такое представление соответствует разбиению числа на двузначные "грани" (справа налево). Пусть

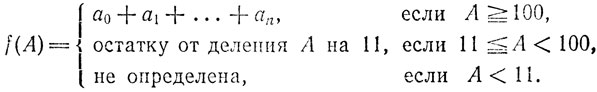
Нам остается указать, что числа А и f(A) действительно равноостаточны при делении на 11 и, кроме того, f(A) < A.

Другой признак равноостаточности при делении на 11 получается на основе представления числа A в виде

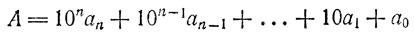
и использования того, что 10 при делении на 11 равноостаточно с -1, а 100 - с 1. Поэтому А равноостаточно с числом а₀ - а₁ + а₂ - а₃ +... ± а_n, и формулировка соответствующего признака равноостаточности не составляет труда.

Наконец, можно, разбивая число А на трехзначные "грани", представить его в виде

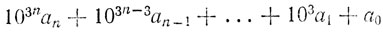
(0 ≤ a_i < 1000). Тогда А при делении на 37 равноостаточно с суммой а₀ + a₁ + ... + a_n, а при делении на 7, 11, 13 - со знакопеременной суммой а₀ - a₁ + a₂ - ... ± a_n.

37. Для примера рассмотрим признак равноостаточности на 8 в троичной системе счисления. Представим для этого произвольное А в виде

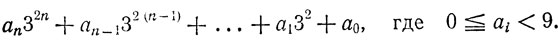
Здесь a_i суть двузначные грани, на которые разбивается число А, считая справа налево. Нам остается положить

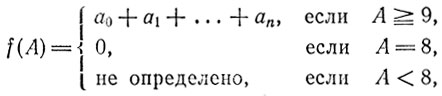
и провести стандартные рассуждения.

38. В шестеричной системе счисления: 5 (k = 1), 7 (k = 2), 43 (k = 3);

В семеричной системе счисления: 2, 3, 6 (k = 1),4, 6, 12, 16, 24 (k = 2), 171 (k = 3);

В девятеричной системе счисления: 2, 4, -8 (k = 1),5, 10, 20, 40 (k = 2), 7, 13, 14, 26 и т. д. (k = 3);

5 В тринадцатеричной системе счисления: 2, 3, 4, 6 (k = 1), 7, 14, 21 и т. д. (k = 2).

39. В троичной системе счисления: 2, 4 (k = 1), 8, 12, 24 (k = 2), 13, 26 (k = 3), 41 (k = 4);

В пятеричной системе счисления: 2, 3, 6 (k = 1), 8, 12, 24 (k = 2), 31 (k = 3);

В восьмеричной системе счисления 3, 9 (k = 1),5, 13 (k = 2);

В десятичной системе счисления: 11 (k = 1), 101 (k = 2), 7, 11, 13 (k = 3).

40. Если числа а и b равноостаточны, то (а - b)m. Поэтому в силу теоремы 6 числа а и b делятся или не делятся на m одновременно.

Числа 4 и 5 равноделимы, но не равноостаточны при делении на 3.

41. Пусть из равноделимости на m следует равно остаточность при делении на m. Это значит, что все не делящиеся на m числа имеют при делении на m один и тот же остаток. Значит, этот остаток должен быть равен единице, так что m = 2.

42. Отношение равноделимости на m, очевидно, является рефлексивным (всякое число равноделимо на m с самим собой), симметричным (если а равноделимо с b, то и b равноделимо с а) и транзитивным (если а равноделимо с b, а b равноделимо с с, то и а равноделимо с с).

Следовательно, это и есть отношение эквивалентности. При этом в один класс попадают все числа, делящиеся на b, а в другой - все не делящиеся на m.

43. Нетрудно проверить, что при m > 2 равноделимость сумм не следует из равноделимости слагаемых.

Для того чтобы равноделимость произведений вытекала из равноделимости их сомножителей, необходимо и достаточно, чтобы число m было простым.

В самом деле, если одно из произведений делится на простое р, то по теореме 13 на это р должен делиться хотя бы один из сомножителей этого произведения. Но тогда на р делится равноделимый ему сомножитель другого произведения, а потому и все произведение. Если же одно произведение на р не делится, то и другое на р делиться не может (ибо в противном случае, на основании только что установленного, на р делилось бы и первое произведение).

Наоборот, если число р составное, то произведения равноделимых сомножителей могут уже равно-4 делимыми не быть. Достаточно положить р = р₁р₂ (p₁ ≠ 1, р₂ ≠ 1). Тогда числа 1 и p₁, а также числа 1 и р₂ равноделимы на р, а произведения 1×1 и p₁×p₂, очевидно, нет.

44. Непосредственное следствие задачи 36.

45. Выполнение условий а) и б) очевидно.

Если, далее, а - 2b ≥ 0, то, очевидно, f(A) < A. Если же а - 2b < 0, то это неравенство может и нарушиться. При этом наибольшее значение модуля |а - 2b| достигается при а = 0 и b = 9 и равно 18. Следовательно, при А ≥ 19 должно быть f(A) < A. Справедливость этого неравенства при меньших значениях обеспечивается определением функции f.

Наконец, 10а + b равноделимо на 7 с 50а + 56 (ибо числа 5 и 7 взаимно простые) и тем самым с 50а + 5b - 7 (7а + b) = а - 2b.

46. Число 15 при делении на 7 дает в остатке 1, а 1 - 2×5 = -9 дает в остатке 5.

47. Условие в) f(A) < A означает а + 4b < 10а + b, т. е. 3b < 9а. Поэтому при а ≥ 4 нужное условие выполняется.

Условие г) очевидно, 10а + b при делении на 13 равноделимо с 40а + 4b, а последнее число равноостаточно с а + 4b.

48. Признак делимости утратит результативность, так как f(39) = 39.

49. Пусть нам нужно построить признак делимости на некоторое m. Постараемся подобрать такое s, взаимно простое с m и по возможности небольшое, что (10s + 1) m (так было в случае m = 7; s оказалось равным 3) или же (10s - 1) m (например, при m = 13, s = 4).

В первом из этих случаев А = 10а + b равноделимо на m с

т. e. с a - bs, а во втором - с

т. e. с a + bs.

В связи со сказанным число 10a + b

при делении на 17 равноделимо с а - 5b,

Завершение точных формулировок этих признаков делимости предоставляется читателю.

50. а) Так как 100 при делении на 49 равноостаточно с 2, всякое число вида

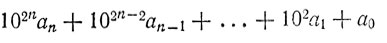
при делении на 49 равноостаточно с

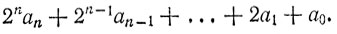
б) 10a + b при делении на 49 равноделимо с a + 5b.

51. Очевидно, при А ≥ 6 должно быть f(A) < A.

52. а) В семеричной системе счисления представление А в виде 7 а + b дает, что при делении на 5 число А равноделимо с a + 3b;

б) В одиннадцатиричной системе счисления представление А в виде 11а + b дает, что при делении на 7 число А равноделимо с а + 2b;

в) В двенадцатиричной системе счисления, представляя А в виде 12а + b, получаем, что при делении на 17 число равноделимо с а - 7b.

53. Условия а) и б) выполняются автоматически. Условия в) и г) соблюдаются потому, что переход от A к F(A) сводится к замене некоторых чисел на их остатки при делении на А (которые меньше самих чисел и равноостаточны с ними).

54. а) r₂ = r₃ = ... = r_n = 0, т. е. r_k = 0 (k ≥ 2);

б) r₃ = r₄ = ... = r_n = 0, т. е. r_k = 0 (k ≥ 3);

в) r₁ = r₂ =... = r_n = 1, т. е. r_k = 1;

г) r₁ = r₃ = . . . = r_2t-1 = -1, r₂ = r₄ = r_2t = 1, т. е. r_k = (-1)^k;

д) r_6t+1 = 3, r_6t+2 = 2, r_6t+3 = 6, r_6t+4 = 4, r_6t+5 = 5, r_6t = 1.

55. Предоставляется читателю.

56. Возьмем произвольное m и положим

r₁ равным остатку от деления t на m,

r₂ >> >> >> tr₁ на m

и т. д. Тогда число

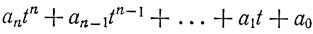
при делении на m равноостаточно с числом

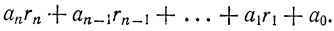
После этого построение требуемого признака не составляет труда.

57. Предоставляется читателю.

58. 10² = 7×¹⁴ + 2, так что r = 2, и мы имеем

А₀ = 1 048 576, А₁ = 1×23 + 4×22 + 85×2 + 76 = 270, A₂ = 2×2 + 70 = 74, A₃ = 4.

59. Если t равноостаточно с r = r₁ при делении на m, то

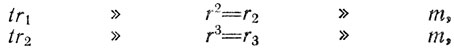
и т. д.

60. Ни 2⁴ - 2, ни 2³ - 1 не делятся на 4.

61. Если ар, то ар, и теорема доказана. Если же а не делится на р, то а взаимно просто с р, и мы можем приведенное в условии теоремы сравнение сократить:

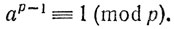
Для доказательства последнего сравнения разделим каждое из чисел вида ta (t = 1, 2, ..., р - 1) на р с остатком:

Это можно переписать так:

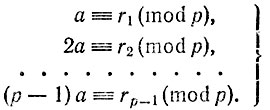
Из результата задачи 26 следует, что среди чисел r_t ровно по одному разу встретится каждое из чисел 1, 2, ..., р - 1. Перемножая все сравнения, мы получаем

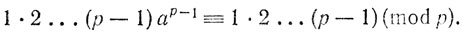
Нам остается это сравнение сократить на 1×2 ...(р - 1).

62.

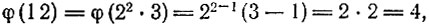
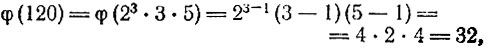
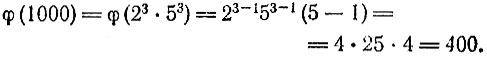
63. Будем искать m в виде p₁^α₁p₂^α₂...p_k^α_k. Тогда

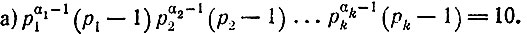
Стоящее слева произведение должно делиться на 5. Значит, либо одно из чисел p₁, р₂,...,p_k есть 5 (пусть для определенности р₁ = 5), либо на 5 делится одна из разностей p₁ - 1, p₂ - 1,....,p_k - 1 (пусть в этом случае (p₁ - 1)5). В первом из этих случаев p₁ - 1 = 4, чего не может быть, так как 10 на 4 не делится. Второй случай, поскольку р₁ должно быть простым числом и 10(p₁ - 1), возможен лишь при p₁ = 11. Но тогда α₁ = 1, и из теоремы 25 следует, что

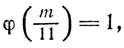
т. е. либо m ÷ 11 = 1 либо m ÷ 11 = 2.

В итоге мы имеем m₁ = 11, m₂ = 22.

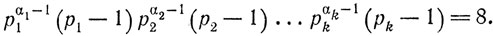
Если m нечетное, то α₁ = α₂ = ... = α_k = 1 (ибо правая часть написанного равенства есть степень двойки):

Это возможно лишь при k = 2, p₁ = 3, р₂ = 5, т. е. при m = 15.

Пусть теперь число m - четное. Положим для определенности p₁ = 2. Очевидно, по-прежнему α₂ = ... = α_k = 1, и мы имеем

Очевидно, α ≤ 4. Если а = 1, то случай подобен рассмотренному: написанное неравенство возможно так же лишь при k = 3, р₂ = 3, р₃ = 5, т. е. при m = 30.

Если α = 2, то k = 2, р₃ = 5 и m = 20.

Если а = 3, то k = 2, р₂ = 3 и m = 24.

Если, наконец, а = 4, то k = 1 и m = 16.

Итак, решения нашей задачи: m₁ = 15, m₂ = 30, m₃ = 20, m₄ = 24, m₅ = 16.

64. Предположим, что

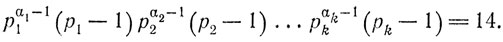
Каждое из чисел вида p_i - 1 есть либо единица, либо четное число, и потому не может быть семеркой. Будучи на единицу меньше простого числа, оно не может равняться 14. Значит, семеркой является одно из чисел р_i^α_i-1. Но тогда p_i - 1 = 6, а 14 на 6 не делится.

65. Пусть m = p₁^α₁p₂^α₂...p_k^α_k. Рассмотрим сначала случай, когда m есть степень простого числа: m = р^α. Для того чтобы некоторое число было взаимно простым с m, необходимо и достаточно, чтобы оно не делилось на р. Но среди чисел 0, 1, 2, ..., m - 1 имеется всего m ÷ p делящихся на р чисел. Следовательно, взаимно простых с р чисел в этом списке имеется столько:

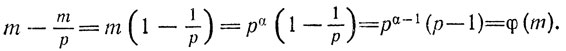
Заметим теперь, что для взаимной простоты а и m необходимо и достаточно, чтобы с а был взаимно прост остаток от деления а на m.

По только что установленному число остатков от деления на p_i^α_i взаимно простых с p_i^α_i, равно φ(p_i^α_i). Но, как было выяснено в процессе решения задачи 28, из равноостаточности чисел при делении на все p_i^α_i следует их равноостаточность при делении на m, и наоборот. Кроме того, для взаимной простоты некоторого числа с m необходимо и достаточно, чтобы оно было взаимно просто с каждым из чисел

Следовательно, каждой комбинации остатков от деления на p₁^α₁,p₂^α₂,...,p_k^α_k взаимно простых с соответствующими делителями, соответствует ровно один остаток от деления на m, взаимно простой с m. Нам остается заметить, что число таких комбинаций остатков равно

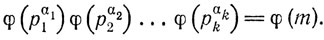
66. Мы имеем

Поэтому

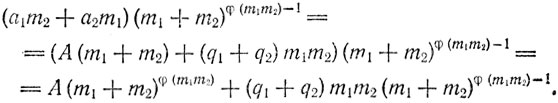
Здесь по теореме Эйлера первое слагаемое при делении на m₁m₂ равноостаточно с A, а второе делится на m₁m₂. Значит, вся сумма при делении на m₁m₂ равдростаточна с А.

67. Предоставляется читателю.

68. Предоставляется читателю.

69. Предоставляется читателю.

70. n¹³ - n = n(n¹² - 1). Но

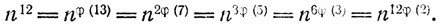
Поэтому либо n p, либо (n¹² - 1) р для р = 2, 3, 5, 7,13. Остается сослаться на теорему 16.

71. Предоставляется читателю.

72. Предоставляется читателю.

73. Пусть наибольший общий делитель чисел а и b есть d. Если с не делится на d, то уравнение

в целых числах неразрешимо. Если же с делится на d, то обе части уравнения можно сократить на d, и мы подходим к уже рассмотренному случаю.

74. Пусть А и В таковы, что

Положим

Тогда

и (x_t,y_t) действительно является решением нашего уравнения.

75. а) x_t = 9 × 5⁵ + 7t = 28 125 + 7t,

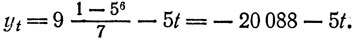
Поскольку свободные члены и коэффициенты при t в выражениях для x_t и y_t, так сказать, "примерно пропорциональны", мы можем надеяться получить представления наших решений в меньших числах.

В самом деле, мы можем написать:

или, полагая

мы получаем

Заметим, что способ решения уравнений в целых числах, приведенный в задаче 74, позволяет обходиться меньшими числами, хотя и требует несколько более сложных вычислений.

б) Воспользуемся тем, что 25 по модулю 13 при-надлежит показателю 2. Мы можем написать:

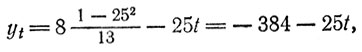
или, после упрощений,

76. Условие в) обеспечивается автоматически, а условие г) следует из теоремы 25.

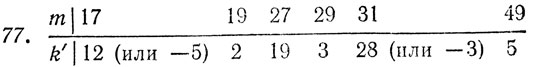
78. Предоставляется читателю.

79. Предоставляется читателю.

80. a) 8^φ(21)-1 = 8¹¹ = 64⁵×8. При делении на 21 это число равноостаточно с 8. Значит, числа 8а + b и а + 8b равноделимы на 21.

б) 12^φ(31)-1 = 12²⁹ = (12²)¹⁴×12 = 144¹⁴×12 при делении на 31 равноостаточно с 11¹⁴×12 = 12¹⁷×12 = (-3)⁷×12 = -(3³)²×3×12 = -(31 -4)²(31 + 5), что равноостаточно с -16×5 = -80. Последнее число очевидно равноостаточно с 13. Значит, числа 12а + b и а + 13b равноделимы на 31