§ 5. Делимость степеней

1. Начнем с описания процесса, который можно было бы назвать "очень общим признаком равно-остаточности".

Пусть k - некоторое натуральное число и r есть остаток от деления t^k на m:

По следствию теоремы 20 (см. п. 3 § 2) при любом n числа rⁿ и t^kn при делении на m также должны быть равно-остаточными.

Составим теперь для произвольного числа А его разбиение на k-значные "грани" справа налево, т. е. представим его в виде

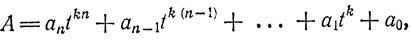
где

и положим

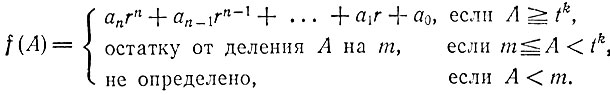
Ясно, что, как и ранее в аналогичных случаях, процесс построения чисел

является признаком равно-остаточности.

Задача 57. Убедиться все-таки в том, что это действительно так.

Задача 58. Полагая t = 10 и k = 2, найти остаток от деления числа 1 048 576 на 7.

Задача 59. Убедиться в том, что только что описанный признак равноостаточности является лишь более явной формой того обобщения признака Паскаля, которое было упомянуто в задаче 56.

2. Говоря формально, при составлении в п. 1 общего признака равноостаточности мы пользовались свойствами степеней, относящимися к их делимости. Однако вопрос о делимости степеней по существу является вопросом о делимости некоторых произведений. Поэтому и решить этот вопрос в принципе удалось на основе результатов § 2. Вместе с тем практическая реализация полученного признака равно-остаточности для тех или иных комбинаций значений чисел t и m может приводить к крупным значениям k и r, так что вычисление значений функции f может потребовать выполнения значительных вычислений, возможно даже превосходящих по объему выкладки по непосредственному делению на m.

Ясно, что вычисление значений функции f оказывается тем проще, чем меньшими будут значения чисел k и r. Разумеется, наиболее удобным оказывается в этом отношении тот случай, когда r - 1. Тогда значение f получается в результате выполнения наименее трудоемкого действия: сложения.

Согласно теореме 22 этот случай (r = 1) имеет место тогда и только тогда, когда (t^k - 1) m или, иными словами, когда t^k при делении на m дает в остатке 1. Встает вопрос: найдется ли при данных t и m такое k, что (t^k - 1) m?

Все сказанное приводит к необходимости заняться изучением делимости степеней несколько более подробно.

3. Расширим несколько наши познания в области теории чисел.

Теорема 24 (теорема Ферма).Если число р простое, то разность а^р - а делится на р.

Не следует путать эту так называемую "малую теорему Ферма" с "великой теоремой Ферма". Последняя утверждает, что при целом n > 2 не существует таких целых а, b и с, что аⁿ + bⁿ = cⁿ. Несмотря на многочисленные попытки, великая теорема Ферма до сих пор не доказана и не опровергнута.

Следствие. Если р - простое и а не делится на р, то а^р-1 - 1 делится на р.

Задача 60. Привести пример, показывающий, что как теорема 24, так и ее следствие для составного р, вообще говоря, неверны.

Задача 61. Доказать теорему Ферма, опираясь на результат задачи 26.

Пусть натуральное число m имеет каноническое разложение:

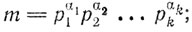
положим

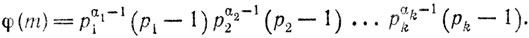
Формулы (5.1) и (5.2) ставят в соответствие каждому натуральному числу m некоторое вполне определенное число φ(m). Это значит, что мы можем говорить о функции φ от натурального аргумента.

Определение. Определенная выше функция φ называется функцией Эйлера.

Функция Эйлера играет исключительно важную роль во многих вопросах теории чисел. Даже в этой книжке будет указано несколько применений этой функции.

Теорема 25. При взаимно простых m₁ и m₂ имеет место равенство

Задача 62. Вычислить φ(12), φ(120), φ(1000).

Задача 63. Определить все числа m, для которых:

а) φ(m) = 10;

б) φ(m) = 8.

Задача 64. Доказать, что не существует такого m, для которого φ(m) = 14.

Задача 65. Показать, что φ(m) равно числу натуральных чисел, взаимно простых с m и меньших m. Это свойство функции Эйлера является чрезвычайно важным. Его часто принимают за определение этой функции.

Теорема 26 (теорема Эйлера). Если числа а и m взаимно просты, то а^φ(m) - 1 делится на m.

Остатки при делении одного и того же делимого на различные делители связаны между собой достаточно сложным образом. Из теоремы Эйлера можно получить принципиально важную для нас зависимость остатков от деления на взаимно простые множители и от деления на их произведение.

Задача 66. Пусть (m₁,m₂) = 1, а a₁ и а₂ - числа, равно-остаточные с А при делении соответственно на m₁ и m₂. Тогда равно-остаточным с А при делении на m₁m₂ будет число

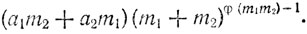
4. На основании установленных фактов мы можем сформулировать общий признак равно-остаточности для произвольного делителя т в произвольной системе счисления t в той явной и достаточно удобной форме, о которой говорилось в п. 1.

Напомним снова, что всякий признак равноостаточности есть алгорифм, т. е. некоторый процесс, и потому всякое его описание должно носить характер развивающегося повествования.

Итак, пусть нам даны числа m и t. Представим m в виде такого произведения m = m₁m₂, что (m₁,t) = 1, и для некоторого показателя k имеет место делимость t^k m₂. Согласно теореме 18 такое представление возможно. В силу задачи 66 вопрос о равно-остаточности при делении на m₁m₂ может быть сведен к аналогичным вопросам для деления на m₁ и m₂. Но признак равно-остаточности на m₂ содержится в теореме 21, а признак равно-остаточности на m₁ - в теореме 22. После применения этих признаков равно-остаточности следует воспользоваться результатом задачи 66.

Например, в случае нахождения признака равно-остаточности при делении на 12 в десятичной системе счисления, очевидно, m₁ = 3, m₂ = 4 и k = 2.

Описанный процесс является общим признаком равно-остаточности в том смысле, что по любому m он выдает некоторый конкретный признак равно-остаточности. Это вытекает из алгорифмичности предоставления числа m в форме, указываемой в теореме 18, а сама эта алгорифмичность следует из алгорифмичности построения канонического разложения чисел (см. п. 9 § 3) .

Нам остается сформулировать в явном виде указанный признак равно-остаточности при делении на m₁, пользуясь возможностью определить показатель k на основании теоремы Эйлера.

5. Применяя доказанные теоремы, построим несколько общих признаков делимости и равно-остаточности.

Фиксируем натуральное m и представим число А в виде

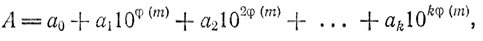
где

т. е. все a_i (i = 0, 1, ..., k) являются φ(m)-значными числами.

Функция

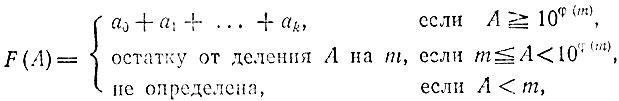
определяет, как нетрудно проверить, некоторый общий признак равно-остаточности.

Задача 67. Проверить это обстоятельство.

Теорема 27. Если числа а и m взаимно просты, а числа k₁ и k₂ равно-остаточны при делении на φ(m), то числа a^k₁ и a^k₂ равно-остаточны при делении на m.

Задача 68. Сформулировать получаемые на основе этого общего признака равно-остаточности конкретные признаки равно-остаточности при делении на 7, 11 и 13.

Задача 69. Сформулировать аналогичный общий признак равно-остаточности для произвольной Личной системы счисления. Убедиться в том, что получаемый так общий признак равно-остаточности по своей формулировке не зависит от основания системы счисления t.

Задача 70. Доказать, что (n¹³ - n) 2730.

6. Построенный общий признак равно-остаточности не является во многих случаях, так сказать, "достаточно экономным", так как число φ(m) может, вообще говоря, оказаться довольно большим.

Поэтому, с одной стороны, при пользовании этим признаком приходится складывать большие числа, а с другой стороны, φ(m)-значные числа при этом приходится делить на т непосредственно (или же пользоваться каким-нибудь другим признаком делимости и равно-остаточности). Желательно поэтому попытаться взять вместо φ(m) другой, меньший показатель. В ряде случаев это удается сделать. Например, при m = 37 вместо φ(m) = 36 можно взять показатель 3, ибо 1000 при делении на 37 дает в остатке единицу; при m = 11 вместо φ(m) = 10 можно взять показатель 2 и т. д.

Определение. Наименьшее число δ, для которого а^δ при делении на m с остатком дает в остатке 1, называется показателем, которому принадлежит число а при делении на m с остатком.

Чаще это число принято называть показателем, которому принадлежит число а по модулю m.

Очевидно, каковы бы ни были взаимно простые числа а и m, показатель δ, которому принадлежит а при делении на m, не превосходит φ(m). Этот показатель и можно взять вместо φ(m) в формулировке общего признака равно-остаточности из п. 5.

Задача 71. Модифицировать построенный общий признак делимости, используя вместо φ(m) показатель, которому принадлежит 10 при делении на m с остатком.

Задача 72. То же для t-ичной системы счисления.

7. Показатель, которому принадлежит число а при делении на m, может, вообще говоря, быть и равным φ(m). Например, последовательностью остатков от деления степеней числа 2 на 11 будет

так что при делении на 11 число 2 принадлежит показателю 10. Значит, для применения признака равноостаточности из п. 5 в этом случае приходится брать k = 10 = φ(11).

Однако во многих случаях удается обходиться показателем ¹/₂φ(m). Пусть, например, m есть степень простого числа: m = p^α и р ≠ 2. Тогда φ(m) = p^α-1 (р - 1), и теорема Эйлера приобретает вид: для (а, р) = 1 должно быть (а^pα-1(p-1) - 1)

р^α. Так как число p^α-1(р - 1) четное, последнее делимое есть разность квадратов, и мы имеем

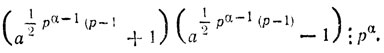
Так как р ≠ 2, оба сомножителя одновременно на р делиться не могут. Значит, на р^α делится либо

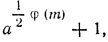
либо

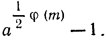
В первом случае мы оказываемся в условиях теоремы 23 с k = ¹/₂φ(m), а во втором - в условиях теоремы 22 с тем же k = ¹/₂φ(m).

8. Применения функции Эйлера и теоремы Эйлера не ограничиваются признаками делимости. Например, при их помощи можно решать уравнения в целых числах.

Теорема 28.Если числа а и b взаимно просты, то уравнение

всегда разрешимо в целых числах, и целыми его решениями будут все пары чисел (x_t,y_t), где

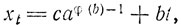
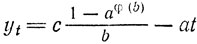
(t - любое целое число).

Задача 73. Доказать теорему, аналогичную теореме 28, не предполагая взаимной простоты чисел а и b.

Задача 74. Найти способ решения уравнений вида (5.3) в целых числах на основе результата задачи 29, б).

Задача 75. Решить в целых числах уравнения:

а) 5x + 7y = 9;

б) 25x + 13y = 8.

9. Теорема 29.Пусть m взаимно просто с 10 и k равно-остаточно с 10^φ(m)-1 при делении на m. Тогда числа

равно делимы на m.

Опираясь на эту теорему, можно построить следующий общий признак делимости. Обозначим через k остаток от деления 10^φ(m)-1 на m с остатком, представим произвольное число А в виде

и положим

Если k велико (близко к m), то вместо него в формулировке соответствующего признака целесообразно брать k - m.

Задача 76. Проверить для функции F выполнение условий а)-в) из п. 10 § 3 и г*) из п. 15 § 3.

Задача 77. На основании только что построенного общего признака делимости вывести признак делимости на числа 17, 19, 27, 29, 31 и 49.

Задача 78. Построить аналогичный общий признак делимости, представляя произвольное натуральное число в виде

и вывести из него признаки делимости на 17, 43, 49,67, 101, 199.

Задача 79. Построить аналогичный общий признак делимости в t-ичной системе счисления.

Задача 80. На основании построенного общего признака делимости вывести конкретные признаки делимости:

а) на число 21 в восьмеричной системе счисления;

б) на число 31 в двенадцатеричной системе счисления.