§ 4. Общие признаки равно-остаточности и делимости

1. Все построенные выше признаки равноостаточности, а также признаки делимости выглядят несколько искусственно, а на первый взгляд может показаться, что эти признаки или, во всяком случае, некоторые из них были найдены случайно или же в результате проб и испытаний. На самом деле это не так. Оказывается, существуют способы построения признаков делимости и равно-остаточности на любое наперед заданное число. Они называются общими признаками делимости или соответственно общими признаками равно-остаточности.

Общие признаки делимости являются способами получения конкретных признаков делимости. Поэтому конкретные признаки делимости можно считать теми результатами, к которым приводят общие признаки. С этой точки зрения общие признаки делимости относятся к конкретным совершенно так же, как конкретный признак делимости относится к результату своего применения к некоторому числу, т. е. к остатку от деления данного числа а на данное число m.

Общие признаки делимости и равно-остаточности напоминают алгорифмы, и притом алгорифмы довольно своеобразные: их итогами, результатами должны быть снова алгорифмы, именно, конкретные признаки делимости или равно-остаточности.

Однако для того чтобы говорить об общих признаках делимости и равно-остаточности как об алгорифмах, мы должны убедиться в том, что они обладают нужными условиями определенности, массовости и результативности.

Говоря подробнее, указывая общий признак делимости (равно как и общий признак равно-остаточности), мы должны проверить выполнение следующих условий. Во-первых, по всякому числу га он должен действительно давать признак делимости (равно-остаточности) на это число. Он должен, так сказать, "перерабатывать" каждое натуральное число га в соответствующий признак. Именно в этом и состоит его результативность. Во-вторых, общий признак должен быть определенным, т. е., примененный к заданному числу га, он должен приводить вполне определенным способом к вполне определенному конкретному признаку делимости (равно-остаточности) на это число. Наконец, в-третьих, признак должен быть массовым, т. е. действительно общим, и давать признаки делимости или равно-остаточности на любое наперед заданное натуральное число.

В этом смысле описанный в п. 6 § 3 способ задания признака равноостаточности, а также описанный в п. 9 § 3 способ нахождения признаков делимости не являются общими признаками. Действительно, указание функций, удовлетворяющих нужным условиям, является процессом, не удовлетворяющим пока ни одному из требований определенности, массовости и результативности.

В самом деле, эти способы не дают нам никакой гарантии в том, что нужная функция будет найдена; значит, они лишены результативности. Далее, если требуемая функция и существует, к ней можно прийти разными путями, не говоря уже о том, что таких функций может оказаться несколько. Значит, эти способы лишены определенности. Наконец, ему не хватает и массовости, так как, быть может, требуемых функций для тех или иных конкретных значений га нам найти не удастся. Сам способ нам, во всяком случае, ничего об этом не говорит. Таким образом, для того чтобы описанный процесс стал алгорифмом, он должен быть еще дополнен точными указаниями, гарантирующими построение вполне определенной функции f_m для каждого конкретного .числа га.

Эта задача "алгорифмизации" построения признаков делимости может быть решена, и даже без особого труда, а общие признаки делимости известны уже давно.

Один такой общий признак равно-остаточности фактически нами уже был построен в п, 11 § 1. при выяснении вопроса о делении с остатком. Мы его можем сформулировать так: каждому целому положительному числу m ставится в соответствие процесс последовательного вычитания этого числа m до получения числа, меньшего чем m (см. последнюю фразу п. 1 § 3). Ясно, что такое соответствие обладает необходимыми свойствами определенности (мы точно знаем, что ставится в соответствие числу m: процесс последовательного вычитания m), массовости (процесс последовательного вычитания можно пытаться применить к любому m) и результативности (такая попытка обязательно приведет к успеху). Однако практическая ценность описанного общего признака равноостаточности весьма невелика.

Некоторое усовершенствование общего признака равноостаточности, основанного на последовательном вычитании, приводит к известному процессу деления целых чисел "углом". Этот процесс деления тоже может рассматриваться как общий признак равноостаточности. Нелишним будет напомнить, что подавляющее большинство людей пользуется при нахождении остатков от деления именно этим признаком. При этом рассуждение ведется по следующей схеме, которую мы воспроизведем в двух вариантах: на обычном житейском языке и на языке алгорифмов.

Общий признак "выдает" результат переработки числа m: конкретный признак равно-остаточности при делении на m, заключающийся в непосредственном делении на m с остатком;

Полученный конкретный признак начинает переработку числа а: деление на m с остатком;

Конкретный признак приводит к цели: к остатку от деления а на m.

В этом рассуждении первые три шага уже очень просты, и поэтому не приходится удивляться, что четвертый шаг, состоящий в фактическом выполнении деления, оказывается таким громоздким. Цель создания общих признаков равно-остаточности и делимости и состоит в разгрузке четвертого шага за счет усовершенствования второго. Именно это и имеют обычно в виду, когда говорят об общих признаках делимости и равно-остаточности.

2. Исторически первым общим признаком делимости (точнее, даже признаком равно-остаточности) является следующий, предложенный знаменитым французским математиком Паскалем еще в середине XVII столетия. Сущность этого признака такова.

Пусть m - натуральное число. Составим последовательность чисел

полагая

и т. д.

Представим теперь произвольное натуральное число А в виде

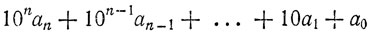
и определим функцию F_m(a) =

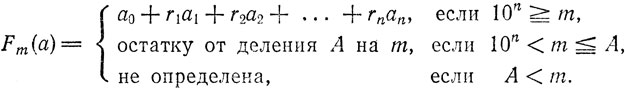
Задача 53. Проверить, что функция F_m при любом m удовлетворяет условиям а)-г) из п. 10 § 3.

Итак, нами построен признак равно-остаточности при делении на произвольное m, т. е. некоторый общий признак равно-остаточности.

Задача 54. Сформулировать получаемые из общего признака равно-остаточности Паскаля признаки равно-остаточности при делении:

а) на 2, 5 и 10;

б) на 4, 20 и 25;

в) на 3 и 9;

г) на 11;

д) на 7.

Задача 55. Пусть в последовательности (12)

и т. д.

Вывести отсюда общий признак равно-остаточности, аналогичный общему признаку равно-остаточности Паскаля.

Задача 56. Вывести общий признак равно-остаточности в t-ичной системе счисления, аналогичный признаку Паскаля.

3. В п. 19 § 3 мы говорили о сравнительных качествах признаков делимости (или равно-остаточности) на данное число. Так как общий признак делимости должен давать нам признаки делимости на любое натуральное число, то неудивительно, что он может для различных чисел приводить к признакам делимости весьма различного качества.

Так, например, общий признак Паскаля наряду с вполне приемлемыми признаками равно-остаточности при делении на 3 и 11 дает весьма громоздкий и неудобный к применению признак равно-остаточности при делении на 7 (см. задачу 54, д)).

В связи с этим по поводу общих признаков делимости и равно-остаточности можно высказать соображения, подобные тем, которые производились в п. 19 § 3 при обсуждении качества конкретных признаков делимости. В этом смысле наилучшим общим признаком делимости (равно-остаточности) должен считаться тот, который в применении к любому наперед заданному целому положительному m дает наилучший признак делимости (равно-остаточности) на это m. Читатель должен отдавать себе отчет в том, что задача нахождения наилучшего общего признака делимости далека не только от своего решения, но даже от строгой постановки.