§ 3. Признаки равно-остаточности и признаки делимости

1. Весьма общий способ нахождения остатка от деления произвольного, но фиксированного натурального числа а на данное натуральное число m заключается в следующем. Будем строить последовательность натуральных чисел

равно-остаточных при делении на m. Способ построения этой последовательности выберем такой, чтобы после всякого ее члена, большего или равного m, следовал еще хотя бы один член. Тогда, очевидно, всякий член последовательности (3.1), меньший чем m (если, конечно, такой существует), будет равен остатку от деления а на m. Таким членом может быть, например, последний член последовательности (опять-таки, если такой имеется).

Одним из простейших примеров последовательности (3.1) может служить последовательность (1.3) из п. 11 § 1:

В сущности, к построению последовательностей такого типа сводятся задачи нахождения остатков в примерах 1 и 2 из предыдущего параграфа.

Всякий способ построения последовательности (3.1), обладающей последним членом, назовем признаком равно-остаточности при делении на m.

Из только что приведенного примера следует, что одним из признаков равно-остаточности при деление на m является процесс последовательного вычитания числа m до получения первого числа, меньшего m.

2. Очевидно, для уверенности в безотказности работы признака равно-остаточности при делении на m необходимо, чтобы он удовлетворял следующим трем требованиям:

1) Признак равно-остаточности должен быть применим к любому натуральному числу а. Иными словами, каково бы ни было число а, конструируемая по нему последовательность (3.1) действительно должна обладать указанным выше свойством: после каждого ее члена, не меньшего чем m, должен следовать еще хотя бы один член. Это свойство признака называется его массовостью.

2) Признак равно-остаточности должен быть точно определенным, т. е. число а должно вполне определять все члены последовательности (3.1), не оставляя места какой-либо произвольности.

3) Наконец, мы должны иметь гарантию того, что в последовательности (3.1) хотя бы один член будет меньше чем т. Это требование будет выполнено, если строить последовательность (3.1) так, чтобы она обязательно имела лишь конечное число членов, т. е. чтобы процесс ее построения не мог продолжаться неопределенно долго, а рано или поздно заканчивался бы появлением остатка от деления а на m. Сформулированное свойство признака равно-остаточности называется его результативностью.

3. Процессы, обладающие свойствами массовости, определенности и результативности, называются алгорифмами и играют в современной математике важную и все более возрастающую роль.

Разумеется, только что приведенная характеризация алгорифма как процесса, обладающего тремя перечисленными свойствами, не является его точным определением. Такое определение, хотя и выработано современной математикой, но сравнительно сложно и не может быть здесь сформулировано. Однако перечисленные предъявляемые к алгорифмам требования довольно полно отражают те условия, которым должны удовлетворять называемые алгорифмами математические процессы. Роль алгорифмов определяется тем, что они являются единообразными способами решения целого ряда однотипных задач. Так, каждый признак равно-остаточности позволяет находить остатки от деления варьируемого числа а на некоторое фиксированное m.

Говоря несколько вольно, к алгорифмам сводятся все те математические задачи, решение которых можно автоматизировать. Поэтому не случайно развитие теории алгорифмов исторически совпало с появлением и распространением электронных вычислительных машин.

К алгорифмам сводятся не только вычислительные задачи в узком смысле этого слова, т. е. такие задачи, в которых по более или менее сложным правилам можно на основе исходных данных получить численный ответ. Можно также ставить вопрос о поисках алгорифма, позволяющего решать любую задачу из некоторой (разумеется, строго очерченной) области математики. Этот алгорифм должен уметь перерабатывать формулировки теорем в их доказательства. Как ни фантастично это может показаться, такие алгорифмы существуют, хотя и не для очень широких областей математики. Вместе с тем для некоторых ее областей (например, для любой области, охватывающей всю арифметику) таких алгорифмов принципиально быть не может.

4. Уточним применительно к признакам равно-остаточности содержание, а также последствия от соблюдения трех предъявляемых к алгорифмам требований.

Из массовости признака равно-остаточности вытекает, что он должен перерабатывать различные числа, и результаты этой переработки также должны быть, вообще говоря, различными (ибо при делении на какое бы то ни было m > 1 не все числа равно-остаточны друг другу). Значит, необходимой составной частью этого процесса должно быть различение чисел (по их величине).

Свойство определенности признака равно-остаточности означает, что уже выписанные числа A₁, A₂,...,A_n последовательности (3.1) должны быть на-столько "опознаваемыми", чтобы на их основании можно было написать следующее число последовательности, А_n+1.

Наконец, свойство результативности влечет, кроме всего прочего, еще и необходимость неограниченных возможностей сравнивать (по величине) получаемое на каждом шаге нашего процесса число А_n с делителем m.

Таким образом, соблюдение каждого из трех требований алгорифмичности для признака равно-остаточности упирается, прежде всего, в необходимость уметь сравнивать в произвольных парах числа по их величине и указывать, если они различны, какое из них больше, а какое - меньше.

5. Только что упомянутая "необходимость уметь", очевидно, также имеет алгорифмическую природу: сравнению по величине должны подлежать любые два натуральных числа (массовость), результатом сравнения может быть не более, чем один ответ: больше, меньше или равно (определенность), и этот ответ должен всегда достигаться (результативность). Значит, мы получаем основание говорить об алгорифмах сравнения двух чисел по величине. Построение такого алгорифма не является столь уж само-очевидным делом, как это могло бы показаться на первый взгляд. Например, вопрос о том, одинаковы или различны числа

и если различны, то какое из них больше, требует для своего решения известных усилий, хотя в действительности первое из этих чисел есть всего-навсего 1, а второе 3.

Ясно, что сравнение по величине чисел из (3.2) затрудняется формой их записи. Следовательно, для построения признаков равно-остаточности весьма важно иметь дело с представлением чисел в такой форме, которая обеспечивала бы возможность их сравнения по величине. Такие формы записи существуют.

Например, ими являются записи чисел в тех или иных (позиционных) системах счисления (см. § 2 п. 2). Алгорифм сравнения двух чисел, записанных в одной и той же системе счисления, состоит в следующем:

1) Сначала в каждом из чисел зачеркиваются цифры по одной (начиная, скажем, справа); если после того, как одно из чисел окажется зачеркнутым полностью, в другом еще останутся цифры, то второе число будет больше первого; если же запасы цифр

в обоих числах будут исчерпаны одновременно, то для сравнения чисел выполняется следующая процедура:

2) Записи сравниваемых чисел восстанавливаются, сравниваются их первые (слева) цифры. При этом большей цифре будет соответствовать большее число; если первые цифры оказываются одинаковыми, то сравниваются вторые цифры и т. д. до первого различия цифр. При этом опять-таки большая цифра будет указывать на большее число. Если все соответственные цифры чисел окажутся одинаковыми, то числа будут равны.

При проведении второй из указанных процедур предполагается, что сравнение по величине однозначных, т. е. меньших чем основание системы счисления, чисел мы производить умеем. Это значит, что в каждой системе счисления исходные значки-цифры заранее задаются в некотором фиксированном порядке; например, в общепринятой десятичной нумерации значок "2" предшествует значку "3" в том смысле, что значок "2" описывает меньшее количество, чем значок "3".

С точки зрения такого алгорифмического сравнения чисел по величине все системы счисления теоретически равноценны. Сравнение же в этом смысле систем счисления по их практическому удобству может служить примером не алгорифмической постановки вопроса (не выполняется условие определенности), и мы на нем останавливаться не будем. Обратим только внимание на то, что в этом вопросе сила привычки к десятичной системе счисления никаких особых преимуществ этой системе не дает.

6. Кроме алгорифмов сравнения чисел, записанных в одной и той же системе счисления, существуют и алгорифмы выполнения арифметических действий над ними. Ими являются общеизвестные (и, очевидно, зависящие лишь несущественным образом от основания системы счисления) способы сложения, вычитания и умножения чисел "столбиком" и их деления "углом". Ясно, что в последнем случае было бы, пожалуй, уместнее говорить не просто о делении, а о делении с остатком.

В случае выполнения действий навыки в обращении с десятичной системой счисления приносят существенное облегчение. Например, выполнение в пятеричной системе счисления действия

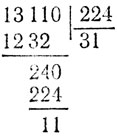
требует известных умственных усилий.

Из алгорифмичности деления с остатком согласно сказанному в п. 2 § 2 вытекает и алгорифмичность перевода записей чисел из одной системы счисления в другую. Следовательно, можно говорить также об алгорифмах сравнения чисел и действий над ними, если они записаны в различных системах счисления. Как дальнейшее следствие, отсюда получается, что алгорифмами являются всевозможные вычисления по арифметическим формулам, в которые вместо букв можно подставлять те или иные числа.

Обратим, наконец, внимание на то, что мы не говорим здесь об алгорифме самого процесса записи произвольно заданных натуральных чисел в той или иной системе счисления, ибо мало ли каким может оказаться это исходное задание.

7. В качестве иллюстративного примера рассмотрим следующее построение. Для каждого натурального числа n составим последовательность a⁽ⁿ⁾₀, a⁽ⁿ⁾₁, a⁽ⁿ⁾₂, ... чисел (цифр), являющихся цифрами бесконечного десятичного разложения числа √n (если число n не является точным квадратом, то эта последовательность, очевидно, оказывается непериодической), и пусть r⁽ⁿ⁾₁, r⁽ⁿ⁾₂ ... - номера всех тех цифр, которые равны нулю; a⁽ⁿ⁾_r⁽ⁿ⁾i = 0 (i = 1,2,...). Если теперь число равных нулю цифр конечно (пусть последнее из них имеет номер r⁽ⁿ⁾_k так что a⁽ⁿ⁾_i > 0 ври i > r⁽ⁿ⁾_k), то положим

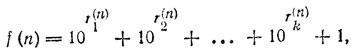
а если их число бесконечно, то положим, скажем, f(n)= 0. Каждое из чисел f(n) является натуральным. Однако едва ли можно говорить об алгорифме, который перерабатывал бы число n в запись числа f(n) в десятичной системе счисления.

Разумеется, вся не алгорифмичность этой конструкции состоит в требовании распознавать, будет ли в десятичном разложении √n конечное или бесконечное число нулей. Между прочим, в известном смысле (в каком именно - мы не станем здесь выяснять) естественно верить, что f(n)= 0 для любого натурального n.

8. Одним из наиболее важных в математике алгорифмов является так называемый алгорифм Евклида, который состоит а следующем.

Пусть а и b - два натуральных числа, причем b > 0. Разделим а на b с остатком: а = bq₀ + r₁ где 0 ≤ r₁ < b. Если r₁ ≠ 0, то мы имеем возможность разделить с остатком b на r₁: b = r₁q₁ + r₂, причем 0 ≤ r₂ < r₁ Продолжая эти последовательные деления с остатком на остаток от предыдущего деления, мы получим дальнейшие равенства: r₁ = r₂q₃ + r₃, r₂ = r₃q₄ + r₄ и т. д.

Покажем, что описанный процесс действительно является алгорифмом, т. е. обладает свойствами определенности, массовости и результативности.

Заметим, что рассматриваемый нами процесс состоит в последовательном выполнении действия деления с остатком.

Поэтому определенность и массовость этого процесса являются следствием неограниченной выполнимости и однозначности действия деления с остатком. Результативность нашего процесса устанавливается также довольно просто. Число b и остатки от делений, составляющих наш процесс, образуют, очевидно, убывающую последовательность неотрицательных чисел;

Но число всех неотрицательных и не превосходящих b чисел равно b + 1. Поэтому и последовательность (3.3) не может насчитывать более чем b членов, так что наш процесс может состоять не более чем из b делений с остатком^*. Таким образом, рассматриваемый процесс действительно является алгорифмом и вполне оправдывает свое название.

^* (На самом деле число этих делений не может превосходить числа 5 log b. Это следует из рассмотрения чисел Фибоначчи (см., например, книжку автора "Числа Фибоначчи", "Наука", 1978, стр. 82-83))

Выясним условия окончания процесса. Очевидно, последнее деление должно быть таким, чтобы дальнейшее деление на его остаток было уже невозможно. Но это может быть лишь в том случае, когда этот последний остаток равен нулю, т. е. когда последнее деление совершилось нацело.

Задача 29. а) Последний отличный от нуля остаток r_n в применении алгорифма Евклида к числам а и b есть (а, b).

б) Каковы бы ни были натуральные а и b, существуют такие целые А и В, что аА + bВ = (а, b).

Задача 30. Вывести из результата б) задачи 29 теоремы 9, 12, 13 и 14. (Подчеркнем, что наши рассуждения, связанные с алгорифмом Евклида, были основаны только на возможности деления с остатком. Мы не пользовались в них ни теоремами 9-14, ни какими-либо иными соображениями, опирающимися на основную теорему арифметики.)

9. Применение алгорифмов (их, так сказать, "работа") может оказаться достаточно громоздким. В качестве примера рассмотрим процесс получения по числу n его канонического разложения (иными словами, алгорифм, перерабатывающий натуральное число в его каноническое разложение). Для оттенения алгорифмической сущности этого процесса включим его, как этап, в процесс последовательного нахождения канонических разложений одного за другим всех натуральных чисел. Это дает нам основание вести рассуждения "по индукции" (см. п. 7 § 1), Предположим, что для всех чисел, меньших n, канонические разложения уже выписаны. Из этого списка можно (вполне алгорифмично) усмотреть, какие из чисел, меньших n, являются простыми. Перечислив их все по возрастанию, будем делить n на каждое из них. Если n разделится на некоторое р, то будет n = n₁p и n₁ < n, а каноническое разложение n₁ в нашем перечне по предположенному уже имеется (ввиду результата задачи 13 нам достаточно произвести деления лишь на те р, которые меньше чем √n) и каноническое разложение получится из канонического разложения n₁ путем увеличения в нем показателя р на единицу.

10. Вернемся, однако, к признакам равно-остаточности. Алгорифмическое построение последовательности (3.1) может быть осуществлено весьма разнообразными путями. Наиболее естественный из них состоит в следующем.

Попробуем найти функцию f(x), подчиненную следующим условиям:

а) Значение f(x) при x ≥ m есть натуральное число;

б) Значение f(x) при x < m не определено (т. е. не имеет смысла);

(Нет ничего удивительного в том, что та или иная функция теряет смысл при некоторых значениях аргумента. Например, не имеет смысла значение функции

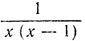
при х = 0 или при x = 1.)

в) Если x ≥ m, то f(x) < x;

г) Если x≥ m то числа x и f(x) равноостаточны при делении на m.

Такие функции существуют. Примером является функция

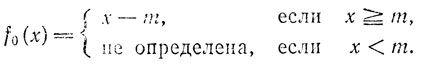
Именно эта функция и осуществляет построение последовательности (1.3) в § 1.

Каждой функции f(x), удовлетворяющей условиям а)-г), отвечает некоторый способ построения последовательности (3.1), т. е. некоторый признак равноостаточности при делении на m.

В самом деле, возьмем произвольное натуральное число а и будем строить последовательность чисел

где

Если A_k ≥ m, то значение функции f(A_k) определено, и потому за А_к следует хотя бы один член. Если же A_k < m , то f(A_k) не определена, и A_k является последним членом последовательности (3.4).

Итак, мы действительно имеем некоторый признак равно-остаточности.

11. Покажем, что найденный признак равно-остаточности обладает всеми тремя свойствами алгорифма.

Условие массовости здесь соблюдается потому, что любое число дает начало некоторой последовательности (3.4), обладающей свойством (3.5).

Условие определенности соблюдается ввиду того, что для вычисления значений f(x) функции f достаточно уметь сравнивать по величине числа хит и выполнять операцию вычитания (отнимания m от x). Обе эти процедуры (если мы имеем дело с числами, записанными в некоторой системе счисления), как было выяснено, являются алгорифмами и тем самым обладают свойством определенности.

Обратимся к условию результативности. По самому своему построению функция f выбрана так, что члены последовательности (3.4) положительны и убывают. Поэтому в ней найдется наименьший неотрицательный член. (Номер этого члена, как нетрудно проверить, не превосходит числа а.) Если бы этот член (обозначим его через α) был больше или хотя бы равен m, то существовало бы значение f(α), по-прежнему неотрицательное, но меньшее α. Значит, член α не был бы последним среди неотрицательных членов последовательности (3.4). Следовательно, последний неотрицательный член (3.4) должен быть меньше, чем m. Но тогда значение f(α) не имеет смысла, и α оказывается вообще последним членом нашей последовательности. Процесс построения последовательности, таким образом, заканчивается, и последний ее член является остатком от деления a на m.

В результате мы установили, что описанный нами признак равно-остаточности действительно обладает требуемыми свойствами определенности, массовости и результативности, т. е. является алгорифмом.

12. Пользуясь изложенным в п. 9 приемом построения признаков равноостаточности, найдем несколько таких признаков. В соответствии со сказанным выше будем считать, что числа, остатки от деления которых требуется найти, записаны в позиционной системе счисления с некоторым основанием t. Признак равно-остаточности при делении на некоторое m перерабатывает в остаток от деления на t фактически не само число, а его запись в соответствующей системе счисления. Поэтому признак равно-остаточности при делении на данное фиксированное число t будет, вообще говоря, зависеть от основания системы счисления. Вместе с тем буквальная формулировка признака равно-остаточности при делении на данное m в t-ичной системе счисления вполне может подходить для признака равно-остаточности при делении на другое m' в системе счисления с другим основанием t'. Соответствующие примеры будут получаться из содержания теорем 19, 20 и 21.

Во избежание возможных недоразумений условимся в дальнейшем как делитель m, так и основание системы счисления t записывать ("называть") в десятичной системе счисления. Так, говоря о признаке равно-остаточности при делении на 12 в семеричной системе счисления, мы будем под 12 понимать именно число 3-4, а не число 3-3 (как это было бы, если бы

число 12 рассматривалось как запись в семеричной системе счисления).

В качестве первого примера найдем признак равно-остаточности при делении на 5 в десятичной си-стеме счисления.

Пусть А - натуральное число. Представим А в виде 10а + b (b - последняя цифра числа А) и положим

Читатель сам может проверить, что так определенная функция удовлетворяет условиям а)-г) п. 10.

Таким образом, для нахождения остатка от деления некоторого числа на 5 достаточно взять последнюю цифру этого числа. Если эта цифра меньше пяти, то она и будет искомым остатком; в противном случае от нее следует отнять 5. Заметим, что применение этого признака равно-остаточности к любому числу приводит к построению последовательности типа (3.4), состоящей не более чем из трех членов.

Разумеется, целью всех проведенных рассуждений является не обнаружение известного всем "признака делимости" на 5, а получение его тем единообразным приемом, который был описан в п. 10.

Задача 31. Указать и проанализировать аналогичные признаки равно-остаточности при делении на 2, 4, 8, 10, 16, 20 и 25 в десятичной системе счисления.

Задача 32. Указать и проанализировать аналогичные признаки равно-остаточности при делении:

а) на 9 и 27 в троичной системе счисления;

б) на 8, 9, 16, 18, 24, 36, 48 и 72 в двенадцатеричной системе счисления.

Задача 33. Представим натуральное число А в виде

и положим

Для каких чисел m такой алгорифм при некотором k является признаком равно-остаточности?

Теорема 21.Представим произвольное натуральное число А в виде at^k + b, где 0 ≤ b < t^k, и положим

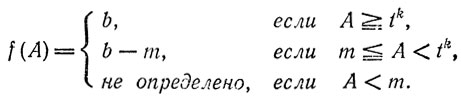
Чтобы для данной функции f алгорифм построения последовательности (3.4) по правилу (3.5) был признаком равно-остаточности при делении на m, необходимо и достаточно, чтобы было t^k m.

13. В качестве второго примера рассмотрим признак равно-остаточности при делении на 3 в десятичной системе счисления.

Запись натурального числа А в десятичной си-стеме счисления имеет вид

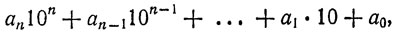
где

Положим

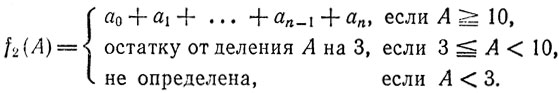
Задача 34. Проверить, что функция f₂(x) удовлетворяет условиям а)-г) и определяет тем самым некоторый признак равно-остаточности при делении на 3.

Задача 35. Применить построенный признак равно-остаточности при делении на 3:

а) к числам 858 773 и 789 988;

б) к числу, десятичная запись которого состоит из 4444 четверок.

Задача 36. Указать и проанализировать аналогичные признаки равно-остаточности при делении на 7, 9, 11, 13 и 37 в десятичной системе счисления.

Задача 37. Указать и проанализировать признаки равно-остаточности при делении:

а) на 2, 4 и 8 в троичной системе счисления;

б) на 2, 4 и 8 в семеричной системе счисления.

Теорема 22.Представим произвольное натуральное число А в виде

где

и положим

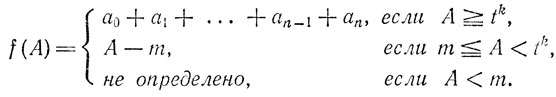
Тогда для того чтобы порождаемый функцией f алгорифм построения последовательности (3.4) по правилу (3.5) был признаком равно-остаточности при делении на m, необходимо и достаточно, чтобы было (t^k - 1) m.

Задача 38. Указать подпадающие под эту теорему признаки равно-остаточности для чисел, записанных в шестеричной, семеричной, девятеричной и тринадцатеричной системах счисления.

Теорема 23. Пусть А - натуральное число, представленное в виде

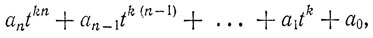
где

Положим

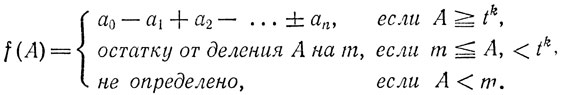
Тогда для того чтобы порождаемый функцией f алгорифм построения последовательности (3.4) по правилу (3.5) был признаком равноостаточности при делении на m, необходимо и достаточно, чтобы было (t^k + 1) m.

Задача 39. Указать подпадающие под эту теорему признаки равно-остаточности для чисел, записанных в троичной, пятеричной, восьмеричной и десятичной системах счисления.

14. Во многих задачах несущественна не только величина неполного частного от деления одного числа на другое, но также и величина остатка от деления, а интересно только, обращается этот остаток в нуль или нет, т. е. делится или нет первое число на второе. После сказанного в п. 1 ясно, как подходить к задачам такого рода.

Назовем числа а и b равноделимыми при делении на m, если либо и а и b делятся на m, либо на m ни а, ни b не делятся.

Задача 40. Каково бы ни было m, любые равно-остаточные при делении на m числа являются равно делимыми на m. Показать на примере, что обратное неверно.

Задача 41. Для каких m из равно делимости двух чисел при делении на m следует их равно-остаточность при этом делении?

Задача 42. Доказать, что отношение равно делимости при делении на данное число m является эквивалентным отношением и разбивает множество целых чисел на два класса.

Задача 43. Будет ли справедлива для равно делимых чисел теорема 20? Ее следствие?

15. Пусть нужно выяснить делимость на т числа А. Будем строить последовательность убывающих натуральных чисел

равно делимых с А при делении на т с остатком. Способ построения последовательности (3.6) выберем такой, чтобы за всяким членом этой последовательности, большим или равным m по абсолютной величине, следовал еще хотя бы один член. Если при этом последний член (3.6) будет равен нулю, то А делится на m, а если не равен нулю, то не делится.

Всякий способ построения последовательности (3.6) назовем признаком делимости на m.

Задача 44. Доказать, что всякий признак равно-остаточности при делении на m является признаком делимости на m.

Очевидно, признаки делимости должны быть алгорифмичными, т. е. удовлетворять таким же условиям определенности, массовости и результативности, что и признаки равноостаточности.

Нетрудно проверить (это предоставляется читателю), что при помощи всякой функции f(x), удовлетворяющей условиям а)-в) из п. 10 и условию г*) если f(x) имеет смысл, то числа х и f(x) равноделимы на m, можно построить признак делимости на т точно таким же образом, как строился признак равно-остаточности при делении на m по всякой функции, удовлетворяющей условиям а)-г).

Найдем несколько признаков делимости.

Согласно теореме 16 достаточно уметь определять делимость чисел на числа вида (степени простого числа).

16. Признак делимости на 7 в десятичной системе счисления. Пусть А - натуральное число. Представим А в виде 10а + b, где 0 ≤ b < 10, как это уже делалось раньше. Положим

Задача 45. Проверить выполнение для функции f₃(A) условий а)-в) и г*).

Функция f₃(A) дает нам известный признак делимости на 7: число 10а + b (0 ≤ b < 10) делится на 7 тогда и только тогда, когда на 7 делится число а - 2b; полученное число снова проверяется этим же способом на делимость на 7 и т. д.

Задача 46. Доказать, что полученный признак делимости на 7 не является признаком равно-остаточности при делении на 7 с остатком.

17. Признак делимости на 13. Представим натуральное число А в виде 10а + b и положим

Задача 47. Проверить выполнение условий а)-в) и г*) для функции f₄(x) и сформулировать полученный признак делимости на 13.?

Задача 48. К каким последствиям приведет замена в определении функции f₄ числа 40 на меньшее?

Задача 49. По аналогии с построенными признаками делимости на 7 и 13 построить аналогичные признаки делимости на 17, 19, 23, 29 и 31.

Задача 50. Построить два признака делимости ка 49.

18. Признаки делимости того же типа имеются и для чисел, записанных в других, не десятичных системах счисления.

Признак делимости на 11 в шестеричной системе счисления. Представим натуральное число А в виде 6а + b, где 0 ≤ b < 6 (в соответствии со сказанным выше все рассуждения ведутся с употреблением обозначений и названий чисел в десятичной системе счисления), и положим

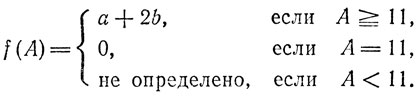
Задача 51. Проверить соблюдение условий а)-в) и г*) для функции f и сформулировать полученный признак делимости.

Задача 52. По аналогии с только что построенным признаком делимости построить признаки делимости:

а) на 5 в семеричной системе счисления;

б) на 7 в одиннадцатеричной системе счисления;

в) на 17 в двенадцатеричной системе счисления.

19. В предыдущих пунктах этого параграфа мы познакомились с большим количеством самых разнообразных признаков равно-остаточности и признаков делимости. Практической целью построения всех этих признаков является получение удобно работающих алгорифмов нахождения остатков при делении на некоторые определенные числа (признаки равно-остаточности) или алгорифмов, обнаруживающих, равны эти остатки нулю или нет (признаки делимости). Насколько же мы осуществили поставленную цель?

Некоторые признаки равно-остаточности, такие, как при делении на 2, 3, 5, 10 в десятичной системе счисления (и вообще - на делитель степени основания системы счисления) действительно оказались весьма практичными и удобными. Применение других

признаков связано с более или менее громоздкими вычислениями.

Естественно поэтому искать и применять такие признаки делимости и равно-остаточности, использование которых приводит к цели по возможности более простым путем.

Одна из трудностей, с которой мы сталкиваемся при такого рода попытках, состоит в том, что мы должны уметь простоту (или, наоборот, сложность) применения того или иного признака оценивать некоторым числом. В качестве такой числовой характеристики можно, например, взять число арифметических действий над однозначными числами, которые необходимо произвести в процессе применения данного признака к тому или иному числу.

К сожалению, всякая такая характеристика объема вычислений в сильной мере зависит от индивидуальных свойств того числа, делимость которого мы хотим испытать.

Так, например, очень легко убедиться в том, что остаток от деления числа 31 025 на 8 есть 1. Для этого достаточно найти остаток от деления на 8 числа 25. Но для нахождения остатка от деления 30 525 на 8 следует разделить на 8 с остатком число 525, а это уже требует большего числа выкладок (безразлично, проводимых в уме или на бумаге).

В качестве другого примера рассмотрим признак равноостаточности при делении на 37 (см. задачу 36). Остаток от деления на 37 числа 10 014 023 находится сложением 10 + 14 + 23 и делением полученной суммы на 37. Остаток, как легко видеть, равен 10. Однако немногие смогут в уме применить этот признак равно-остаточности к числу 782 639 485.

Поэтому, говоря об удобстве использования признаков делимости и равноостаточности, мы должны отвлекаться от сложностей индивидуальных испытаний чисел на делимость, а оценивать возможности каждого признака "в среднем". При таком подходе мы можем надеяться точно сформулировать меру сложности признака делимости или равно-остаточности и даже найти наиболее экономный в этом смысле признак. К сожалению, мы лишены здесь возможности развивать эту сторону вопроса более подробно.