§ 2. Делимость сумм и произведений

1. Во многих случаях при делении с остатком интересно найти именно остаток от деления числа а на число b, а величина неполного частного от деления не играет роли.

Пусть, например, мы хотим узнать, какой день недели будет 1 января 2000 г. (разумеется, если до того срока сохранится действующий в настоящее время календарь). Легко справиться по календарю, что 1 января 1980 г. - вторник. Двадцать лет, разделяющие эти даты, состоят из 20×365 + 4 (последнее слагаемое - число високосных лет за это время), т. е. из 7305 дней. Эти дни составляют 1043 целых недель и еще 4 дня. По прошествии 1043 целых недель снова наступит вторник, так что еще через 4 дня, 1 января 2000 г., будет суббота. Очевидно, для решения поставленной нами сейчас перед собой задачи совершенно неважно знать, сколько именно целых недель прошло за 20 лет, а интересно только число дней, прошедших сверх этих недель.

С задачами такого рода приходится иногда сталкиваться историкам, особенно востоковедам, при со-поставлении дат, указанных по разным календарям.

Казалось бы, для нахождения остатка от деления одного числа на другое проще всего произвести деление с остатком непосредственно. Однако практически выполнить такое деление нередко представляется весьма затруднительным, особенно если подлежащее исследованию делимое задано в виде некоторого сложного выражения, вроде, скажем, 2¹⁰⁰⁰ + 3¹⁰⁰⁰. Вместе с тем львиная доля этой работы будет потрачена на нахождение неполного частного, которое нам само по себе не нужно. Необходимо поэтому попытаться выработать способ нахождения остатка непосредственно, минуя вычисление неполного частного.

Продемонстрируем один из таких приемов на только что решавшейся нами задаче о дате 1 января 2000 г. Мы Можем рассуждать следующим образом. Каждый простой (не високосный) год состоит из 365 дней, что составляет 52 полные недели и еще один день. Високосный же год составляет столько же недель и два дня. Значит, весь срок от 1 января 1980 г. до 1 января 2000 г. состоит из некоторого (совершенно неважно, какого) числа полных недель плюс число дней, равное числу содержащихся в этом сроке лет, причем каждый високосный год считается за два. Это число дней равно 20 + 5 = 25. Исключив из него 3 полных недели, получаем 4 дня, которые и следует отсчитывать от нашего вторника. Оказывается, такая "замена года днем" есть проявление весьма общего приема, изучением которого мы сейчас и займемся.

2. Другой пример, когда целью деления с остатком является получение именно остатка, а неполное частное рассматривается лишь как исходный материал для дальнейших операций, доставляет нам запись чисел в той или иной позиционной системе счисления. Напомним, что число А называется записанным в (позиционной) системе счисления с основанием t, или, короче, в t-ичной системе счисления (где t - целое положительное число, большее единицы), если оно представлено в виде

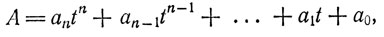
где

Числа a₀, a₁, ..., a_n называются t-ичными цифрами числа A^*.

При t = 10 мы получаем десятичную систему счисления. Запись числа в этой системе настолько привычна для нас, что говоря о числе, мы обычно только в этой форме его себе и представляем. В действительности, однако, если соображения привычности перестают играть роль, как это, например, имеет место при фиксации чисел в электронных вычислительных машинах, более удобными могут оказаться и другие системы счисления (двоичная, восьмеричная и т. д.).

^* (Элементарное, но вместе с тем глубокое изложение вопросов, связанных с системами счисления, содержится в брошюре С. В. Фомина "Системы счисления" ("Наука", 1908).)

Так как мы в этой книжке не будем рассматривать не позиционных систем счисления (например, записей чисел "римскими" цифрами), мы далее указание на их позиционность будем, как правило, опускать.

Ясно, что из (2.1) следует

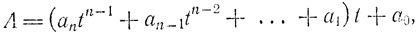
т. е. последняя t-ичная цифра а₀ числа А является остатком от деления А на t с остатком. Неполное частное от такого деления стоит здесь в скобках. Разделив это неполное частное на t с остатком, мы получим

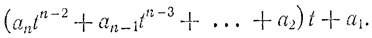
Остатком оказывается предпоследняя Личная цифра числа А. Продолжая этот процесс повторного деления с остатком на t, мы будем последовательно получать все t-ичные цифры числа А, считая справа налево (т. е., от низших разрядов к высшим). Очевидно (а точнее - в силу полной упорядоченности множества натуральных чисел по величине), этот процесс последовательного деления с остатком должен рано или поздно оборваться. В результате мы получим все t-ичные цифры числа А, т. е. его запись в t-ичной системе счисления.

Так, в частности, осуществляется перевод чисел из одной системы счисления в другую. Например,

Поэтому 10 000 в шестеричной системе счисления записывается как 114 144.

3.Определение. Назовем числа а и b равно-остаточными при делении на b, если остатки от деления а и b на m равны.

Установим несколько свойств равно-остаточных чисел.

Теорема 19. Для того чтобы числа а и b были равно-остаточными при делении на m, необходимо и достаточно, чтобы (а - b) m.

Следствие. Если числа а и b равно-остаточны при делении на m, и m d, то а и b равно-остаточны при делении на d.

Теорема 20. Если при делении на m числа a₁,a₂,...,a_n соответственно равно-остаточны числам b₁,₂,...,b_n, то равно-остаточными будут суммы a₁ + a₂ + ... + a_n и b₁ + b₂ + ... + b_n, а также произведения a₁a₂....a_n и b₁b₂....b_n.

Следствие. Если при делении на m числа а и b равно-остаточны, то такими же являются и степени aⁿ и bⁿ при любом натуральном n.

Теорема 20 и ее следствие дают уже довольно богатые возможности для нахождения остатков от деления.

Приведем несколько примеров.

Пример 1. Найти остаток от деления на 3 числа

Очевидно, при делении на 3 число 13 равно-остаточно с 1, 2 равно-остаточно с -1, а 5 тоже с -1. Значит, на основании доказанного число А при делении на 3 равно-остаточно с числом

т. е. искомый остаток равен нулю, а А делится на 3.

Пример 2. Найти остаток от деления того же числа А на 37.

Представим для этого А в следующем виде:

Так как 13² = 169 при делении на 37 равно-остаточно с - 16, 2⁵ = 32 равно-остаточно с - 5, а 5³ = 125 - с + 14, то все число А равно-остаточно с

или, что то же самое, с

Но 16², т. е. 256, равно-остаточно с - 3, а 70 - с - 4. Значит, А равно-остаточно с

или, что то же самое, с

а потому с

Наконец, 56 при делении на 37 равно-остаточно с 19, Которое неотрицательно и меньше 37 и потому является искомым остатком.

Задача 21. Найти остаток от деления:

а) А = (116 + 17¹⁷)²¹ на 8;

б) А = 14²⁵⁶ на 17.

Задача 22. Доказать, что при любом n:

а) (n³ + 11n) 6;

б) (4ⁿ + 15n - 1) 9;

в) (10³ⁿ - 1) 3ⁿ⁺²;

г) При любом а

д) При любом k

(n^k - 1 ) (n - 1);

е) При любом нечетном k

(n^k + 1) (n + 1).

4. Равноостаточные при делении на m числа а и b называются также сравнимыми по модулю m. Это обозначается так:

а сама эта формула называется сравнением.

Сравнимость двух чисел по некоторому фиксированному модулю m или, что то же самое, их равно-остаточность при делении на ь, также является некоторым отношением, связывающим между собой целые числа.

Отметим несколько свойств отношения сравнимости по модулю.

1° Рефлексивность: а ≡ a(mod m).

Действительно, а - а = 0 m.

2° Симметричность: если a ≡ b (mod m), то b ≡ a(mod m).

В самом деле, если (а - b) m, то (хотя бы по теореме 5) и (b - а) m.

3° Транзитивность: если a ≡ b (mod m) и b ≡ c(mod m), то а ≡ с (mod m).

Для доказательства достаточно заметить, что из (а - b) m и (b - с) m по теореме 6 следует, что (а - с) m.

Если некоторое отношение (обозначим его через ~) обладает свойствами рефлексивности, симметричности и транзитивности, то оно называется отношением эквивалентности (или эквивалентным отношением). Простейшим примером отношения эквивалентности на множестве чисел является отношение равенства.

Задача 23. Эквивалентное отношение ~ на множестве чисел разбивает это множество на такие классы (называемые классами эквивалентности), что любые два числа из одного класса связаны отношением эквивалентности, а никакие два числа из разных классов этим отношением не связаны. (Доказать.)

В этой задаче речь идет об отношении эквивалентности, связывающем числа. Однако это несущественно, и утверждение задачи справедливо для эквивалентных отношений, связывающих объекты совершенно произвольной природы.

Так как отношение сравнимости по модулю m - отношение эквивалентности, оно также разбивает множество целых чисел на классы. Эти классы называют классами вычетов по модулю m.

4° Число классов вычетов по модулю m равно m.

В самом деле, два числа а и b принадлежат одному классу, вычетов по модулю m тогда и только тогда, когда они при делении на m дают один и тот же остаток. Но остаток при делении на m может принимать ровно m значений: 0, 1, 2,... , m - 1. Следовательно, и число классов равно m.

Отметим одно чрезвычайно интересное обстоятельство, являющееся уточнением следствия теоремы 19.

Для того чтобы каждый класс вычетов по модулю m₁ содержался в некотором классе вычетов по модулю m₂, необходимо и достаточно, чтобы m₁ m₂.

Действительно, рассмотрим класс вычетов K₁ по модулю m₁ содержащий число 0. Очевидно, класс K₁ состоит из всех чисел дающих при делении на m₁ в остатке 0, т. е. делящихся на m₁. В частности, он содержит число m₁. Класс вычетов по модулю m₂, содержащий K₁, также содержит 0 и потому состоит из всех чисел, делящихся на m₂. Так как в него входит число m₁, должно быть m₁ m₂. Этим доказана необходимость, достаточность же очевидна.

Таким образом, отношение делимости можно определить через соотношения между классами вычетов. Этот прием позволяет определять делимость для объектов гораздо более общей и сложной природы, чем натуральные числа. Последовательное развитие этих идей приводит к теории групп, важной отрасли современной алгебры, имеющей приложения в теоретической физике и кристаллографии.

Продолжим перечисление свойств сравнимости чисел. Из теоремы 20 немедленно следуют:

5° Если a ≡ b (mod m) и с ≡ d(mod m), то

Следствие. Если а ≡ b (mod m), то

для любого целого r.

6° Если а ≡ b (mod m) и с ≡ d(mod m), то

Свойства 5° и 6° показывают, что сравнения подобно равенствам можно почленно складывать и перемножать.

Задача 24. Если на множестве целых чисел задано эквивалентное отношение ~, разбивающее это множество на т классов, и такое, что из а ~ b и с ~ d следует а + с ~ b + d, то отношение ~ есть сравнимость по модулю т (т. е. а ~ b тогда и только тогда, когда а = b(modm)).

Задача 25. Сформулировать и доказать правила сокращения сравнений.

Задача 26. Если число р простое и а не делится на р, то никакие два числа из а, 2а, 3а, ..., (р - 1)а не сравнимы друг с другом по модулю р. Поэтому при делении на р чисел а, 2а, 3а,..., (р - 1)а мы получим по одному разу все остатки, кроме нуля.

Задача 27 (теорема Вильсона). Для того чтобы число р было простым, необходимо и достаточно, чтобы (р - 1)! + 1 = 1⋅2 ... (р - 1) + 1 делилось на р.

Задача 28. Сформулировать и доказать для равно-остаточности теорему, аналогичную теореме 16,